蒋家沟泥石流阵流的时空特征
2014-05-06李泳
李泳
教授,中国科学院山地灾害与地表过程重点实验室,中国科学院水利部成都山地灾害与环境研究所,成都610041
蒋家沟泥石流阵流的时空特征
李泳
教授,中国科学院山地灾害与地表过程重点实验室,中国科学院水利部成都山地灾害与环境研究所,成都610041
泥石流;阵流;时空特征;系统动力学
间歇性阵流是黏性泥石流的基本活动形式,普遍发生于世界各地,而以云南昆明东川的蒋家沟表现最为典型,观测数据也最为系统。每场泥石流表现为一个阵流序列,序列呈现出整体性和非线性特征。阵流流量涨落达3个数量级,均值随时间衰减;序列Hurst指数大于0.5,说明具有一定的长程关联性;阵流间歇时间呈负幂函数分布,阵流有时空聚集性。在参数空间中,阵流点成团聚集,点之间的欧氏距离呈一定形式的标度分布。这些特征意味着阵流序列蕴含着泥石流发生的系统动力学背景。
泥石流(特别是黏性泥石流)都以阵流形式运动。“阵流”是重力流的普遍形式[1-2],表现为一个独立的流动物质单元,在一般高密度流体中,指以有限的空间延展和确定的几何形态运动的流体[1]。泥石流仿佛一列火车在沟谷运动,它有突然涌起的“头”和逐渐衰落的“尾”。在最早的泥石流的科学论文里,就有对阵流的生动描述[3-4]。世界各地泥石流都有阵流的报道,有的发生在一般山区,有的是火山碎屑流[4-9]。
关于阵流的研究,大多关注流体特性,将其归结为流体不稳定性[10]、流体结构特性[11]或各种形式的波(如动力波[12])。这些研究虽然回答了泥石流为什么会以阵流形态运动,却忽略了阵流作为流域现象的一个基本特征:阵流往往具有不同的物质组成、流态、流速和流量,因而不可能是同一个“母流”自发分裂形成的。实际上,不同的阵流有着不同的起源。泥石流物源是随机分布的,物源活动是不连续、非均匀的,因而间歇性的泥石流阵流,除了流体不稳定性的自发形成以外,更多是由流域物质和活动的时空分布决定的。
昆明东川的蒋家沟是世界著名的泥石流景观流域,在过去的50多年里,年均泥石流10次,其频率之高是世界罕见的。每场泥石流由几十至几百个阵流组成,阵流物质组成变化大,流态多,流量涨落显著,蕴涵着丰富的泥石流动力学和流域活动的信息。自1960年以来,中国科学院东川泥石流观测研究站对蒋家沟泥石流进行了持续的实时观测,获取了完整而系统的数据,为阵流的分析研究提供了良好的基础。阵流的数据特征可以证明,泥石流是流域的非线性系统行为。
1 泥石流形成的基本问题
蒋家沟泥石流观测和源地泥石流启动实验表明,阵流的形成经历三个过程(图1):
(1)坡面过程:源地坡面土体在降雨作用下产生崩塌、滑坡等,是泥石流的物质来源。坡面过程取决于土体和降水的相互作用,依赖于土体结构(如颗粒组成、孔隙度、含水量等)、孔隙水压、渗流和坡面径流等参数。坡面过程表现了沙堆模型所呈现的自组织临界特征[13],例如崩塌(滑坡)的频率-规模关系呈负幂函数,因而泥石流源区物质的补给是不连续和非均匀的。
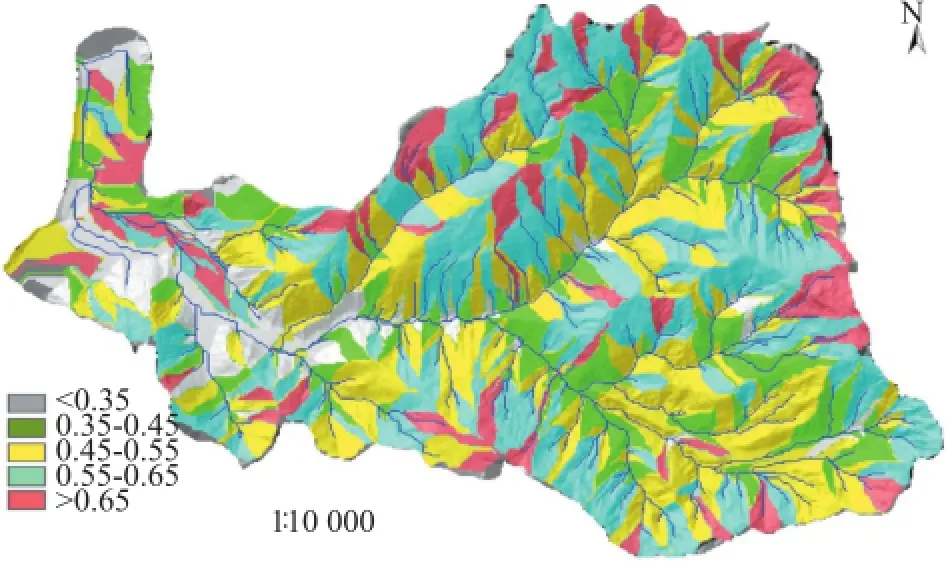
图1 蒋家沟泥石流源区分布
(2)沟谷过程:进入沟道的崩塌(滑坡)土体或沟道本来松散的泥沙堆积,在流水作用下液化,形成支沟泥石流,满足一定条件(如一定流量、沟道摩擦、流体屈服应力等)时,支沟泥石流能持续向下游流动。以Bingham体模型为例,流动应满足剪切力大于屈服应力,即τ<ρgjh[14],其中τ为土体的屈服应力,ρ为密度,g为重力加速度,j为沟谷比降,h为流深。为了满足这个条件,流动的土体可能会“等待”更多的物质(坡面来的或沟谷补充的)。
(3)汇流过程:不同支沟泥石流向下游汇聚,形成主沟泥石流。汇流的实现依赖于支沟泥石流的形成和延续、沟道的连通以及各支流的“同步”。其中涉及众多影响因子和条件,迄今尚不能确定具体的“临界条件”。
总之,源地的随机分布、土体的非均匀结构、降雨的空间差异以及不同条件的流域分支和流通路径,决定了泥石流从源地到沟谷发展潜藏着随机性和不确定性。因此,同一个流域在相似条件下也会发生不同的泥石流。目前尚无系统理论能“正面”解决以上问题,但阵流的多样性一定隐含着泥石流发生的系统信息,因而可以从阵流的特征反推泥石流形成和发展的动力学背景。
2 阵流序列的涨落与衰减
每一场泥石流通常包含几十甚至几百个阵流。图2是蒋家沟看到的阵流龙头、叠加和堆积的情景。如果忽略阵流内部的物质组成和运动的变化(那主要是动力学关心的问题),那么可将一场泥石流看成一个阵流序列:

其中X为实时观测的阵流参数,如速度(v)、流体密度(ρ)、流量(Q)和总量(R)等,N为一场泥石流的阵流数(所有参数都用国际单位制)。

图2 泥石流阵流的运动和堆积
不同场次的泥石流具有不同的序列模式(图3为3场泥石流的流量序列),但都表现出以下共同特征:
(1)多数阵流的持续时间在50 s以内,阵流间歇时间约为100 s,而且间歇时间满足负幂分布。
(2)在若干高密度“大”阵流(流量大)之间总会出现持续时间特别长的1个或多个低密度“小”阵流(流量小)。“大阵流” 是高密度泥石流(通常ρ>2),小阵流是稀性泥石流或高含沙水流(ρ<1.6)。
(3)阵流有不同的密度、速度和流量,流量涨落可达3个数量级。

图3 泥石流阵流的流量序列
从流量序列方差VarQ(n) 随阵次n的变化曲线(图4)可见,阵流序列具有强烈的变异性。更重要的是,这种现象是整体性的,而不是局域性的。也就是说,一个序列的任何部分都不会表现这种特征。整体行为更显著地表现为平均流量随阵次的变化:令〈Q〉n= (Q1+ Q2+ … +Qn)/n,则在一定阵次之后,均值〈Q〉n以负幂形式n–a衰减,这与均值趋于定值的随机序列是完全不同的[15]。

图4 阵流序列流量方差随阵次的变化
3 阵流序列的Hurst指数
阵流序列的整体性意味着阵次之间的关联性,可用Hurst指数来描述[16]。考虑序列的极差(R)与方差(S)之比随阵次的变化,如果满足

H 即Hurst指数,其中R(τ) = max X (t,τ)-min X (t, τ)为给定阵次下的极差。表1是几场泥石流的流量、速度、间歇时间和单个阵流总量序列的Hurst指数,几乎都是H>0.5(图5)。

表1 阵流序列的Hurst指数

图5 阵流序列的Hurst指数曲线
对完全随机的序列(如随机游走或分式Brown运动)来说,H=0.5,说明序列的点之间没有任何关联。当H>0.5时,说明序列具有正的自相关性(图6),流量序列的自相关关系不等于零而是随阵次而衰减,说明阵流序列存在一定的长程关联性(即持续性)。阵流的多变性与持续性,体现了自然界复杂系统的两个普遍现象——“诺亚(Noah)效应”和“约瑟夫(Joseph)效应”[17],意味着泥石流也是一种系统行为(即流域演化的系统行为),因而具有系统演化的内在特征,而不仅取决于环境因子的影响。例如,因为内在的涨落特征,即使在普通的情况下,也可能产生大规模的泥石流,而极端条件(如超强雨量)未必产生极端的泥石流。

图6 流量序列的自相关系数
4 泥石流参数的概率分布
虽然泥石流表现多样,涨落悬殊,但也呈现着一些共同特征,特别是参数的概率分布。如速度、流深和流量都满足Weibull分布[18],而流量分布的特殊还体现了最大流量在阵流序列的主导作用。对一般Weibull分布而言,流量应满足

有趣的是,指数b≈1而系数a与最大流量存在良好的负幂函数关系:a~Qm–β,这里β= 0.982 1。若令Q*= Q/Qm,则分布为P(>Q*) = K exp (– a*Q*) ,其中a* = Qm1–β= Qm
0.0179≈1,因而不同序列都归结为简单的指数函数exp (– Q*)(图7),这说明指数分布是一个普适的规律。

图7 阵流流量的指数分布
参数分布的统一性还有更直观的表示。将阵流看成参数空间的点,考虑三个参数:流速(v)、流量(Q)和时间间隔(τ),它们分别代表阵流的空间运动、规模和阵流的发生时间,则一个泥石流事件为参数空间的一个点列P(Vi, Qi, τi) (i=1, 2, 3 ,…, N,N为事件的阵流总数)。阵流参数随阵次变化的均值定义为Xi= Xi/〈X〉i,其中〈X〉i为参数X在前i阵的平均。以此均值来标度各参数,则阵流点在参数空间的分布如图8所示。在图8中,原来的多个量级的涨落被“消减”了,所有点都相对集中在一个小区域内。
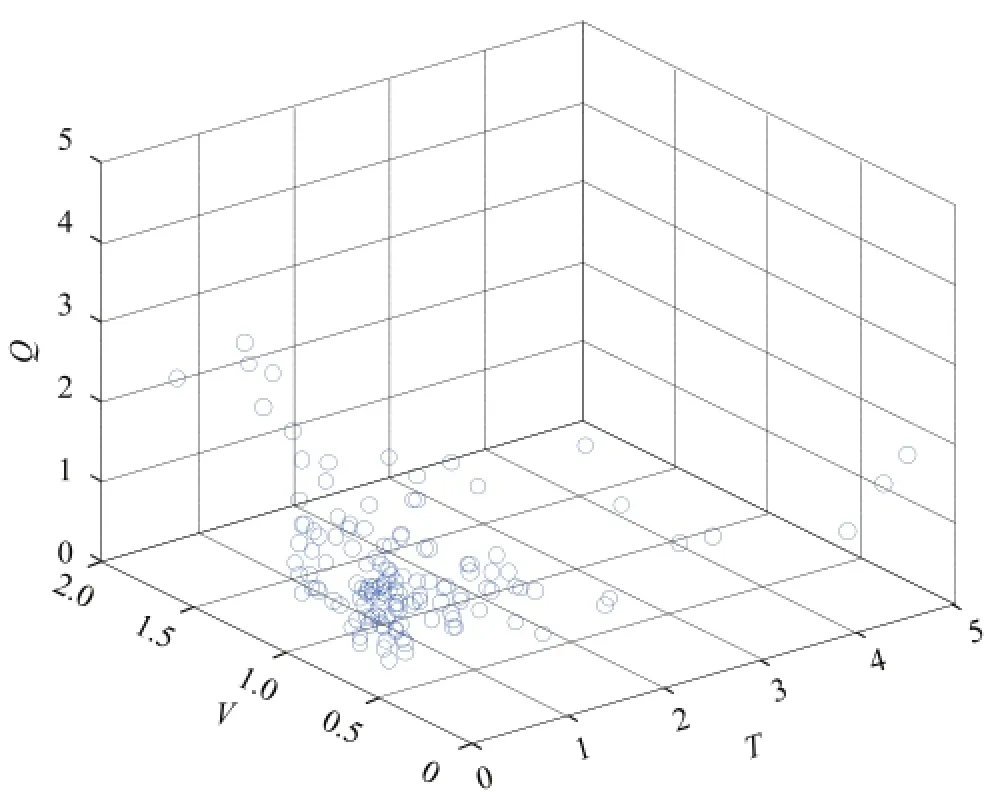
图8 事件空间中的阵流点(910709序列)
在参数空间中,时间相继的两个阵流之间的“间隔”,可用两点的欧氏距离R来表示。一个阵流序列(P1, P2, P3, …, PN)对应一个间隔序列(R1, R2, …, RN–1)。蒋家沟的数据计算表明,90%以上的阵流间隔都落在区间(0.1,3)内。进一步计算可以发现R的分布满足
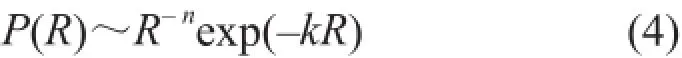
图9是不同泥石流事件的R分布曲线,几乎都落在同一条曲线上。可见,不论泥石流事件如何不同(不同的阵次、规模、性质等),在参数空间都服从相同的分布,说明它们具有内在的一致性。
阵流点在参数空间的聚集,符合阵流的间歇时间短、大阵流成群出现的现象(如图3),也是Noah效应与Joseph效应的几何表现。参数空间的几何结构和拓扑结构,可能蕴涵着泥石流系统行为的更多特征。
5 结论与讨论
一场泥石流就是一个阵流序列,尽管序列长短不同、形态多样、涨落悬殊,但都呈现出统一的时空特征。如:
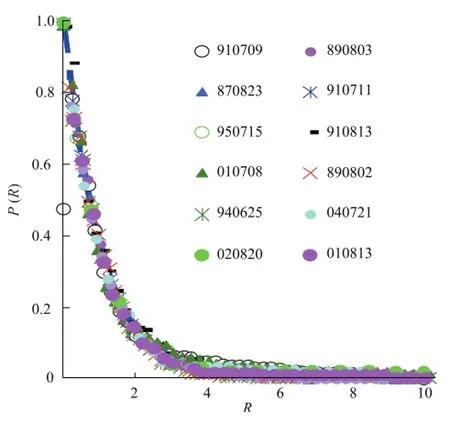
图9 时空间隔的集中分布
(1)自相关性:阵流参数(如流量、流速和间歇时间)序列的Hurst指数都大于0.5。
(2)相似的概率分布:阵流参数都满足Weibull分布。
(3)时空聚集性:泥石流事件在参数空间中表现为一个聚集的点集,相邻阵流的时空间隔满足相同形式的标度分布。
以上特征说明了泥石流活动的系统性,是复杂系统普遍存在的Noah效应和Joseph效应的具体表现。相似的数据特征意味着泥石流具有相同的动力学机制——这里不是指单个阵流发生和运动的土力学或流体动力学的机制,而是指阵流序列所蕴含的系统动力学机制,是与流域系统(而不是流体运动)相关的动力学机制。
以往的泥石流研究基于线性思维,例如将泥石流的预测问题归结为一个或几个因子的临界值问题,但从泥石流的形成过程看,并不存在“抽象的”临界条件,每个过程都有其独特的临界条件,而且临界条件即使满足了,过程也是不确定的。例如源地坡面过程是一种自组织临界过程,是间歇性的、离散的、涨落的、随机的,虽然存在一定的临界条件(如土体破坏准则),但整体过程是不确定的。从系统动力学的角度看,泥石流的发生、演化和预测不仅取决于外在因素的影响(如降雨或地震的激发),还在于系统本身的演化特征。例如泥石流源地坡面过程,即使正常情况下也可能出现大的涨落,因而导致大规模的泥石流。系统的涨落,也意味着同一个流域在相同条件下也不一定产生相同的泥石流。蒋家沟泥石流的多样性就证明了这一点。
(2014年6月23日收稿)■
[1] LAVAL A, CREMER M, BEGHIN P, et al. Density surges: twodimensional experiments [J]. Sedimentology, 1988, 35: 73-84.
[2] SIMPSON J E. Gravity currents in the environment and the laboratory [M]. Cambridge: Cambridge University Press, 1997.
[3] RICKMERS W R. The duab of Turkestan [M]. Cambridge: Cambridge University Press, 1913.
[4] BLACKWELDER E. Mudflows as a geologic agent in semiarid mountains [J]. Geol Soc Am Bull, 1928, 39: 465-480.
[5] CONWAY W M. Exploration in the mustagh Mountains [J]. The Geographical Journal, 1893, 2: 289-303.
[6] PACK F J. Torrential potential of desert waters [J]. Pan-American Geologist, 1923, 40: 349-356.
[7] SHARP R P, NOBLES L H. Mudflow of 1941 at Wrightwood, southern California [J]. Geol Soc Am Bull, 1953, 64: 547-560.
[8] HARRIS S A, GUSTAFSON C A. Debris flow characteristics in an area of continuous permafrost, St. Elias Range, Yukon Territory. Zeits [J]. Geomorphologie, 1993, 37: 41-56.
[9] TAKAHASHI T. Debris flow [M]//IAHR/AIRH Monography Series. Rotterdam: A.A.Balkeman, 1991: 2.
[10] CHIU-ON N, CHIANG C M. Roll wave on a shallow layer of mud modeled as a power-law fluid [J]. J Fluid Mech, 1993, 263:151-183.
[11] HUNGR O. Analysis of debris flow surges using the theory of uniformly progressive flow [J]. Earth Surface Progresses and Landforms, 2000, 25: 483-495.
[12] WEIR G J. Kinematic wave theory for Ruapehu lahars [J]. New Zealand Journal of Science, 1982, 25: 197-203.
[13] BAK P, TANG C, WIESENFELD K. Self-organized criticality [J]. Physical Review A, 1988, 38: 364-374.
[14] JOHNSON A M. Physical processes in geology [M]. San Francisco: Freeman, Cooper & Co, 1970.
[15] LIU J J, LI Y, SU P C, et al. Temporal variation of intermittent surges of debris flow [J]. Journal of Hydrology, 2009, 365(3/4): 322-328.
[16] HURST H E, BLACK R, SINAIKA Y M. Long-Term Storage in Reservoirs: An experimental Study [M]. London: Constable, 1965.
[17] MANDELBROT B B, WALLIS J. Noah, Joseph, and operational hydrology [J]. Water Resources Research, 1968, 4(3): 909-918.
[18] LI Y, LIU J J, HU K H, SU P C, Probability distribution of measured debris-flow velocity in Jiangjia Gully, Yunnan Province, China [J]. Natural Hazards, 2012, 60(2): 689-701.
Spatiotemporal characteristics of debris flow in Jiangjia Gully
LI Yong
Professor, Key Laboratory of Mountain Hazards and Surface Process, Chinese Academy of Sciences, Institute of Mountain Hazards and Environment, Chinese Academy of Sciences & Ministry of Water Conservancy, Chengdu 610041, China
Debris flow over the world always moves in manner of intermittent surges, which is the most conspicuous appearance in Jiangjia Gully (JJG), Yunnan. More than fifty years of real-time observations of living debris flows in JJG have achieved a huge dataset of parameters concerning more than 10 000 surges, from which derive several fundamental features of the surge sequences: probability distribution of the interval, fluctuation and distribution of discharge, decay of the sequence, Hurst index and surge concentration in space and time. All these characteristics suggest that the surge sequence is a systemic behavior of some underlying dynamics and hints at some nonlinear dynamical mechanism of debris flow formation and evolution.
debris flow, surge, spatiotemporal characteristics, systemic dynamics
(编辑:温文)
10.3969/j.issn.0253-9608.2014.05.002
