基于专家经验的振动台控制参数自整定方法研究1

纪金豹 孙丽娟 占鹏云 李 娜 张硕玉

（北京工业大学 工程抗震与结构诊治北京市重点实验室，北京 100124）

基于专家经验的振动台控制参数自整定方法研究1

纪金豹 孙丽娟 占鹏云 李 娜 张硕玉

（北京工业大学 工程抗震与结构诊治北京市重点实验室，北京 100124）

地震模拟振动台控制系统的控制参数较多，其参数手动整定费时费力，尤其对于多振动台台阵系统，其手动整定难度很大。基于上述问题，根据专家进行系统调试的经验，提出了一种振动台控制参数自整定策略，分析了手动整定中各参数对系统性能的影响，给出了自整定算法的整定规则，并通过Matlab仿真进行振动台的控制参数自动整定。通过比较自整定参数和理论计算参数下的时频域特性，验证了本文所给出的自整定算法。结果表明，该方法具有简单实用及较好的实用价值，可供振动台参数自整定研究参考和借鉴。

地震模拟振动台 专家经验 参数自整定

引言

地震模拟振动台是工程抗震领域主要的和可靠的试验设备之一。它在控制过程中面临的最困难的问题就是控制参数的整定问题。振动台一般采用三参量控制算法，三参量控制参数的合理设置是振动台发挥控制性能的关键（Stoten等，2007）。合理的三参量控制参数组合可以拓宽系统有效的频宽。反之，不但无法得到预想的控制效果，还有可能使振动台自激而损坏设备（范顺成，2010）。振动台控制参数的整定主要有理论整定和经验整定。其中，理论整定是基于被控对象的数学模型，通过理论推导计算得到控制器的控制参数；而经验整定是专家通过实践总结出来的调节参数的过程。杨志东（2009）采用根轨迹法描绘出振动台闭环系统极点与控制参数的数值关系，但实际系统模型与理论模型有较大差异，而且计算过程复杂繁琐，得到的参数往往存在很大的误差。韩俊伟（1997）利用实际频率特性对振动台系统控制参数的匹配原理进行了理论和试验研究，结果表明调节原则可保证振动台工作状态最优。但整定过程需要大量的反复调试，既耗时又费力。对于某一特定控制系统，所整定的一组控制参数仅适用于某一工况，而实际工况总是随着被控对象及环境因素等变化而改变。针对上述存在的问题，笔者提出了一种基于专家经验的参数自整定算法，该方法可快速得到最优的三参量控制参数，使控制系统达到最优。

1 地震模拟振动台系统分析

1.1 地震模拟振动台工作原理

地震模拟振动台的工作原理如图1所示。地震波经三参量发生器产生位移、速度和加速度三种信号，与通过传感器采集的位移、加速度反馈信号，以及由两种信号合成的速度反馈信号形成闭环控制系统，经伺服阀将电信号转换成液压信号，从而驱动液压伺服缸，并推动振动台台面和模型试件按期望信号规律振动（陈章位，2010）。

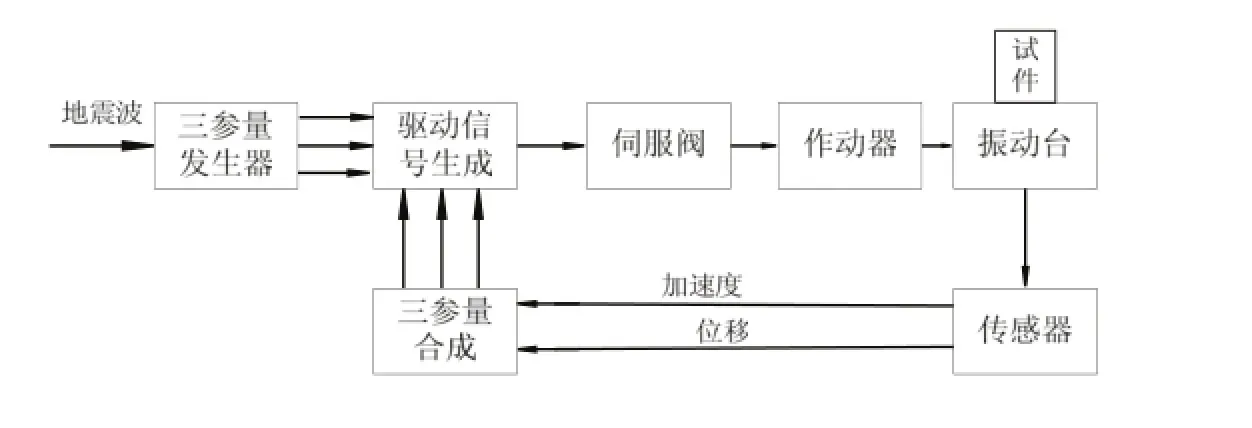
图1 地震模拟振动台控制系统原理图Fig. 1 Principle of shaking table control system

1.2 振动台系统模型

根据液压控制理论，不考虑伺服阀动态特性，振动台系统开环传递函数如下：

式中，0n为液压系统固有频率；0D为液压系统阻尼比；Kv为速度反馈增益；s为积分算子。

本文以北京工业大学工程结构试验中心3m3m×的振动台为研究对象，其性能指标如表1所示。

表1 地震模拟振动台系统性能指标Table 1 The parameters of the shaking table

1.3 三参量控制原理

三参量控制器是地震模拟振动台控制系统的重要组成部分。三参量控制算法主要是为了补偿地震模拟振动台仅有位移控制时频宽小、阻尼小的缺陷，从而更好地实现不同频段的加速度、速度、位移控制。三参量控制中采用位移控制低频段，速度控制中频段，加速度控制高频段，从而实现增大系统阻尼，拓宽系统频带的目的（李振宝，2010）。

控制器主要由三参量反馈控制器和前馈控制器组成。其中，三参量反馈控制器的作用是通过调节afk、vfk和dfk三个反馈系数提高系统阻尼比和共振频率，扩宽系统频率适用范围，增强系统稳定性；而三参量前馈控制器的作用是通过调节ark、vrk和drk三个前馈参数抵消系统闭环传递函数中距离虚轴较近的极点，进一步拓展系统的工作频宽（于浩洋，2013）。三参量控制原理如图2所示，图中0d、0v为滤波器的两参数，VelSyn为速度合成器模块。

图2 三参量控制原理图Fig. 2 Schematic diagram of three-parametric control

2 专家经验参数自整定方法的原理

基于专家经验的参数自整定方法是总结专家的参数整定经验，模拟专家手动整定的过程，利用一系列的整定规则表示专家知识，使参数快速、精确地达到最优值，有效解决地震模拟振动台手动调整参数耗时存在的一些关键问题。以下是根据手动调整台的经验给出的调整规则（黄浩华，2008）。

（1）调节位移反馈增益dA′和位移前馈增益dA

由于振动台采用加速度控制方式，在开环情况下系统无法定位，因此引入位移反馈形成闭环控制系统，可使系统受控。调节增益使加速度前馈aA、速度前馈vA、加速度反馈aA′、速度反馈vA′均为0，逐步调节位移增益。如图3所示，系统的频带宽度随着增益的增大而变宽，且能够明显地看到油柱共振峰，其对应的频率即为油柱共振频率。

图3 仅存在位移反馈时的系统频响特性曲线Fig. 3 Frequency-response curve under displacement feedback

根据手动调整台的经验，调节位移增益一般使平坦部分约在5Hz左右，取图3中0.5—5Hz之间所有点幅值绝对值的平均值小于一个较小的值1ε，使得在此区间范围内的频响曲线尽可能平坦。按式（2）原则对位移增益进行调整：

（2）调节加速度反馈增益Aa′

调节加速度反馈参数可以增大系统的阻尼比，削平油柱共振峰。如图4（a）所示可以看出，逐级增加加速度反馈控制量，油柱共振峰逐渐减小。算法中取油柱共振频率n0左边的上限值频率n0−ω1和右边的下限值n0+ω2频率之间幅值的平均值小于频率n0−ω3处的幅值，如图4（b）所示。按式（3）原则对加速度反馈增益进行调整：

式中，A(n0−ω1∼n0+ω2)为频响图中频率n0−ω1到n0+ω2之间幅值的平均值；A(n0−ω3)为频率n0−ω3点的幅值。

图4 加速度反馈下频响特性曲线Fig. 4 Frequency-response curve under acceleration feedback

（3）调节速度前馈增益vA

速度前馈增益可以调节系统的中频段频宽。如图5所示，随着增益值的增大，中频段更为平坦，取频响图中5—10Hz之间所有点幅值绝对值的平均值小于一个较小的值2ε，使得在此区间范围内的曲线尽可能的平坦。由此给出速度前馈增益的调整规则：

图5 调节速度前馈下频响特性曲线Fig. 5 Frequency-response curve under speed feedforward

（4）调节加速度前馈增益aA

调节加速度前馈增益可以扩展系统的高频段频宽。如图6所示，系统频响特性曲线中的高频部分随着加速度前馈增益的增加呈上升的趋势。取频响图中5—10Hz之间所有点幅值绝对值的平均值小于一个较小的值3ε，使得在此范围区间频响曲线尽可能接近0dB。由此给出加速度前馈增益的调整规则：式中，表示频响图（图6）中，10—45Hz之间幅值绝对值的平均值。

图6 调节加速度前馈下频响特性曲线Fig. 6 Frequency-response curve under acceleration feedforward

（5）如果频宽未达到要求，可调节速度负反馈，且应同时调节加速度负反馈，可达到提高油柱共振频率的目的，且仍可保证不出现油柱共振峰点。然后调节速度和加速度前馈，可进一步拓宽频带。

3 参数自整定算法仿真与对比验证

3.1 参数自整定算法仿真

由以上算法可得到如图7所示的地震模拟振动台控制参数自整定流程图。图7中h1、h2、h3、h4和h5分别为位移增益、加速度反馈增益、速度前馈增益、加速度前馈增益和速度反馈增益的步长，δ1、δ2为较小的固定值，其他参数与前文意义一致。自整定过程的输入信号采用白噪声序列，噪声幅值为0.05g，信号采样时间0.002s，振动台自身的参数取值如表2所示。

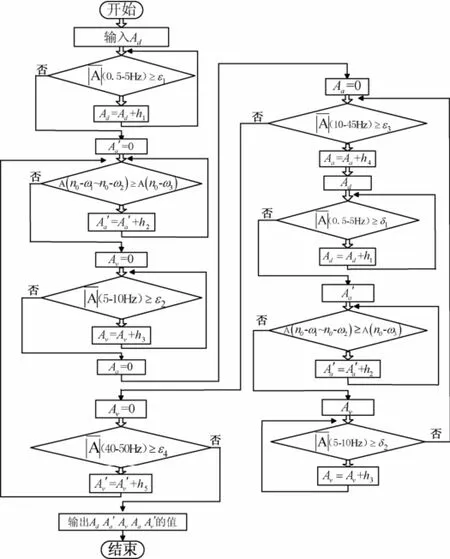
图7 自整定算法流程图Fig. 7 Flow diagram of auto-tuning algorithm

表2 地震模拟振动台仿真参数Table 2 The simulation parameters of shaking table

由振动台的输入、输出数据可得到系统的频响特性，依据建立的规则自动调节控制参数。由上述建立的振动台模型，并考虑伺服阀为二阶振荡环节，伺服阀传递函数如式（7）所示。采用自行编制的自整定程序得到的自整定参数值和采用黄浩华（2008）给出的控制参数计算公式得到的参数值如表3所示。

式中，qn为伺服阀二阶系统固有频率；qD为伺服阀二阶系统阻尼比；s为积分算子。

表3 三参量控制器控制参数值Table 3 Control parameters of TVC

3.2 参数自整定算法对比验证

由表2可以看出，自整定值与理论值存在一定的差异，但其控制效果需通过时频曲线对比才能下结论。以El-centro地震波为例进行系统仿真，对基于专家经验的自整定算法控制效果与理论计算参数的整定效果进行比较，响应曲线如图8所示。由图8（a）可以看出，系统频响曲线在0.5—50Hz范围内较为平坦，基本保持在±3dB范围内；由图8（b）可以看出，输出信号时程曲线吻合较好，信号之间的相关系数可达到0.932，即在工作频宽内输出信号能较好地复现输入控制信号。这些都表明，利用基于专家经验的控制参数自整定算法可以得到较好的控制参数。

4 结论

本文结合地震模拟振动台系统手动整定参数的经验，提出了一种基于专家经验的自整定算法。分析了手动整定过程中各参数对系统性能的影响，以频率响应曲线作为控制器参数自整定的依据，明确了自整定算法的设计步骤。通过Matlab进行的仿真研究表明，此算法简单、有效，且容易被技术人员理解掌握，具有较好的实用价值。

图8 自整定参数下系统仿真结果对比曲线Fig. 8 The system simulation correlation curve with the Auto-tuning parameters

陈章位，2010. 液压振动台控制策略的研究．汽车零部件，（8）：79—82．

范顺成，2010．地震模拟振动台状态控制参数配置的研究．天津：Scientific Research Publishing．USA．

黄浩华，2008．地震模拟振动台的设计与应用技术．北京：地震出版社，57—76．

韩俊伟，1997．地震模拟振动台初始状态调节和控制参数的匹配．地震工程与工程振动，（1）：116—121．

李振宝，2010．地震模拟振动台三参量控制算法超调修正．振动与冲击，10（29）：211—215．

杨志东，2009．液压振动台振动环境模拟的控制技术研究．哈尔滨：哈尔滨工业大学．

于浩洋，2013．电液振动台加速度波形再现控制算法．黑龙江工程学院学报（自然科学版），227（1）：60—63．

Stoten D.P.，Shimizu N.，2007．The feedforward minimal control synthesis algorithm and its application to the control of shaking-tables．Proceedings of the Institution of Mechanical Engineers，Part I． Journal of Systems and Control Engineering，221（3）：423—444．

Control Parameters Auto-Tuning Methods of Shaking Table Based on Expert Experiences

Ji Jinbao，Sun Lijuan，Zhan Pengyun，Li Na and Zhang Shuoyu

（Beijing Laboratory of Earthquake Engineering and Structural Retrofit，Beijing University of Technology，Beijing 100124，China）

The parameter setting manually for the control system is time-consuming，especially for many vibration tables．Based on the experience of expert system for debugging a vibration table control parameter self-tuning strategy，we proposed a method to control parameters setting automatically through Matlab for shaking table．It is proved that our algorithm is correct by setting parameters and theoretical calculation of the time and frequency domain properties．

Shaking table；Specialist experiences；Parameters auto-tuning

纪金豹，孙丽娟，占鹏云，李娜，张硕玉，2014．基于专家经验的振动台控制参数自整定方法研究．震灾防御技术，9（4）：882

．

10.11899/zzfy20140416

1 ［基金项目］ 国家自然科技基金资助项目（51278013，51108428）

2014-04-14

纪金豹，男，生于1974年。高级实验师。主要从事结构振动控制、结构试验技术方面的研究工作。E-mail：jinbao@bjut.edu.cn