比例定理及其在几何上的应用

杨永青

（江苏省高港中等专业学校，江苏 泰州 225300）

比例定理及其在几何上的应用

杨永青

（江苏省高港中等专业学校，江苏 泰州 225300）

证明线段的比例关系是数学几何中的一个难点，我们不妨把证明线段的比例式转化成线段乘积之间的等式，而线段的乘积常常可用面积公式来表示，在证明线段的比例关系时，可用面积比代替线段的比。因此，应用面积关系证明线段的比例式常常是比较简便的。

比例定理；比例关系；几何上的应用

在几何中，把两个线段的比转化为某两个三角形面积的比，这类方程在证明或求解两线段的比的有关问题中用处很大，下面我们将介绍有关这方面的一个命题。

在证明这个命题之前，我们先介绍用来证明这个命题的一个定理，三角形面积的斜高公式。

斜高公式：在ABC中，设BC=a，在直线BC上任取一点P，设AP=b（我们不妨把AP叫作ABC在BC边上的斜高），AP与 BC所成的角（锐角或钝角任取其一）为C，那么有：absinC，其中S△ABC表示△ABC的面积。

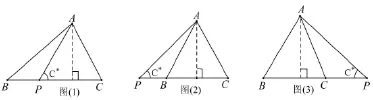
如图（1）的情形，直接应用三角形的面积公式有：

如图（2）的情形，可以由S△ABC=S△APC-S△APB作类似推导证得：

如图（3）的情形也可作类似地证明，这里从略。

下面我们用斜高公式来证明上面所提到的命题—比例定理。

比例定理：若直线PQ交直线AB于M，那么有：

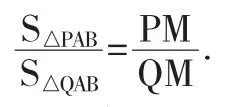
证明点P、Q、A、B的位置有四种情形。

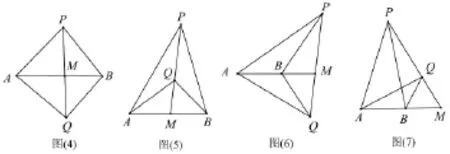
如图（4），由三角形面积的斜高公式有：

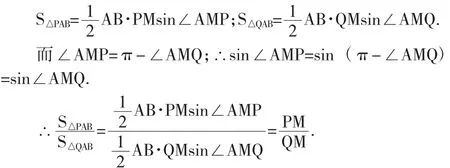
如图（5）、（6）、（7）的情形可作类似推导，这里从略。

下面我们来看看比例定理在几何上的重要应用。

例：如图（10），ABC的中线AD、BE相交于点M，求证：

上例是大家所熟知的命题，读者不妨将这里的证法与教科书上常用证法作下对比，体会一下应用比例定理解题的优点。

G632.0

A

1674-9324（2014）17-0098-01