简支混凝土梁桥Pushover分析简化方法1

王 草包琦玮李全旺

1）清华大学土木工程系，北京 100084

2）北京市市政设计研究总院，北京 100035

简支混凝土梁桥Pushover分析简化方法1

王 草1)包琦玮2)李全旺1)

1）清华大学土木工程系，北京 100084

2）北京市市政设计研究总院，北京 100035

静力Pushover分析方法是研究结构在地震作用下力学性能的非线性分析方法，目前已经得到了广泛的运用。本文主要讨论了对于简支梁桥的简化Pushover分析方法。对于非高墩的规则桥梁，结构的重量主要来自于上部结构，因而可以把分析模型简化为单自由度体系。当给定了墩柱潜在塑性铰区的弯矩-曲率关系曲线后，可以通过简单的运算得到其Pushover曲线，从而避免了有限元建模的麻烦。该方法对于工程运用有着一定的参考价值。最后，结合算例表明了该简化方法的有效性。

简支梁桥 Pushover分析 抗震评估 简化方法

引言

在大震作用下，传统的基于承载力的抗震设计不足以预估结构的变形和结构在大震作用下的实际行为，因此结构基于位移的抗震设计越来越受到重视（毛建猛，2008）。

作为计算结构在地震作用下非线性反应的简便方法，Pushover方法由于原理简单、计算方便且精度满足工程需求，已得到越来越广泛的研究（秦泗凤，2008；马千里等，2008），并已经被国内外的一些规范所采用（中华人民共和国国家标准，2001；FEMA 273，1996）。

在对规则桥梁进行Pushover分析时，当结构的自重主要来自于上部结构时，可以将体系简化为单自由度体系，这样，Pushover分析过程便可以得到进一步简化。

本文首先介绍了静力Pushover分析方法的原理，然后提出了对于简支梁桥的Pushover分析简化方法，最后结合算例说明了该方法的有效性。

1 静力Pushover分析方法

对于n维多自由度体系，若已知其质量矩阵、阻尼矩阵和刚度矩阵分别为M，C和K，则可以基于D' Alembert原理建立其运动方程（刘晶波等，2005）：

对于一个n维线性空间，n个线性无关的向量可以组成一组基；该空间内的其他任意向量可以用这组基的线性组合来表示。容易证明，对于n个自由度体系而言，其n阶主振型{φ1,φ2,…φn}便是其形状向量的一组基。这样，式（1）的解（体系的变形形状向量）可以用φ1，φ2,…φn的线性组合表示：

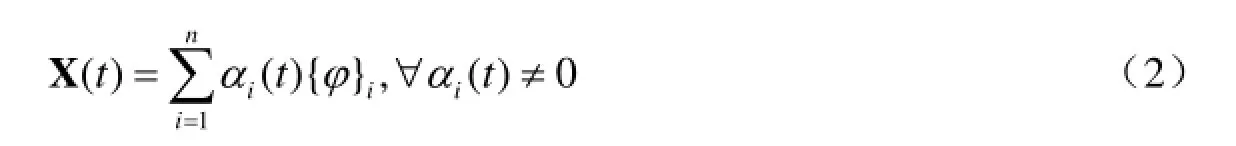
式中，αi(t)为时变广义坐标。

在如此的线性表示下，并假定Rayleigh阻尼，则可以利用主振型向量对M和K的正交性，对式（1）进行解耦：

式中，ξj和ωj分别为第j阶的主振型对应的广义阻尼比和频率；Mj为第j阶广义质量，j=1，2，3，… n。

现考虑由第j振型引起的第i个质点所受的地震力Fij。令，由式（3）可得：

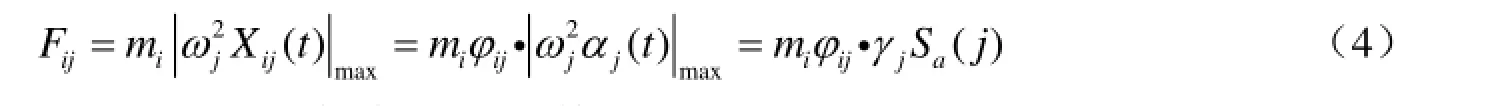
式中，Sa( j )为第j振型对应的加速度谱（Gupta等2000）。

进一步可得：

现对上述n–DOF作如下2点假定：①体系的地震响应仅由基本振型决定；②位移向量x由控制点处的位移xn和结构的基本振型形状向量φ1表示，即x=xnφ1（认为在地震动过程中，结构的变形形状保持不变）。

由上述2点假定，令式（5）中的j=1，则：

另一方面，若xn是向量x中最大的元素，则：

由式（7）可得：

对结构施加逐渐增大的水平力F时，可以得到其“水平力–端顶位移”曲线，称之为Pushover曲线；基于式（6）和式（8）可以将该曲线转化为“位移–加速度”谱曲线，称之为“能力谱曲线”。如图1所示，将能力谱曲线和设计反应谱（需求谱）曲线绘制在同一坐标系中；随着水平力F的增加（沿着能力谱曲线箭头走势），若这2条曲线有交点，则该点所对应的水平位移值xlim即为结构在地震力作用下的最大水平位移响应。然后，若xlim不大于给定的位移阈值，则认为结构在此地震作用下安全；否则，则结构在此地震强度下不安全（Chopra等，2000）。这便是Pushover分析方法的思路。关于xlim的求解方法在众多文献中均有介绍，在此不再赘述（毛建猛，2008；马千里等，2008；Chopra等，2000）。然而需要注意的是，Pushover分析方法是建立在两个简化条件的基础上，而这样的假定在简化问题的同时也会带来一定的计算误差。由此，众多学者在研究中都给出了Pushover分析的改进方法（Chopra等，2002；Fajfar等，1996）。由于本文的主旨是给出Pushover分析的一个简化方法，而非讨论该法的精确程度，故而这些改进算法在下文中不予涉及。

图1 Pushover分析方法图示Fig. 1 Illustration for the Pushover analysis method

2 对于简支梁桥的Pushover简化分析

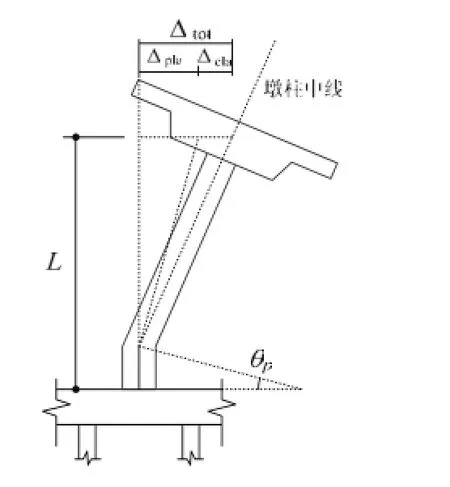
图2 独立墩柱的墩顶水平位移图Fig. 2 Illustration for the horizontal displacement of a single abutment

基于Pushover分析方法求解简支梁桥桥墩的顶部位移时，注意到其较之普通高层建筑结构，有着如下特殊性质：①主要质量集中在顶部，而普通高层建筑的质量沿高度方向分散分布；②在墩顶施加水平作用力，可将墩柱看作一个弹（塑）性杆件来研究其变形问题。

考虑如图2所示的墩柱。当桥墩受到的端顶水平推力较小时，沿墩柱高度方向的弯矩呈线性分布，墩顶处产生的水平位移Δtot在弹性范围内。当水平推力逐渐增加，于墩底处的弯矩值达到截面的屈服弯矩My时，会在墩底处形成塑性铰。

如图3所示，用弹簧模型来模拟塑性铰的力学特征（秦泗凤，2008），其中，Lp为等效塑性铰区的长度。将墩柱的塑性变形等效为Lp长度内的塑性段变形Δpla，则有：

式中，Δela为墩顶处的弹性变形。

对于塑性铰区的截面，为了简化问题，通常可以将其弯矩对曲率的曲线（M-φ曲线）双线性化（中华人民共和国行业标准，2008）。如图4所示，其中φy为截面的屈服曲率；φu为截面的极限曲率。

图3 塑性铰弹簧模型Fig. 3 Spring model for the plastic hinge

图4 弯矩-曲率的双折线化模型Fig. 4 Bilinear model for the moment–curvature curve

由图3则有：

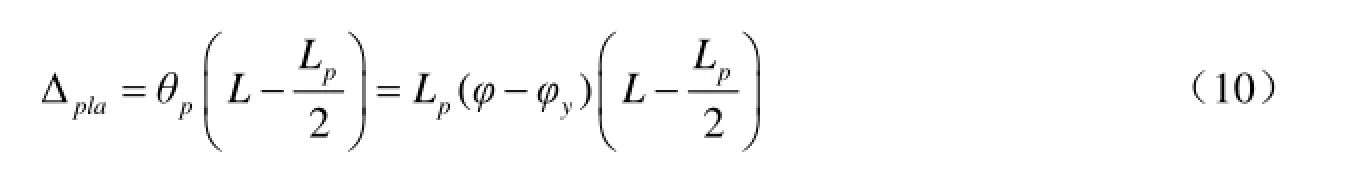
考虑墩顶处的弹性变形量Δela，设曲率沿墩高方向呈线性分布，则有：

将式（10）和式（11b）代入式（9）中，则可以得到在塑性范围内墩柱的水平位移和塑性铰区内截面塑性曲率之间的对应关系：

对于多数简支梁桥或者连续梁桥，认为其结构的主要重量来自于上部结构。在此简化条件下，对图2中的墩柱进行受力分析，同时考虑P–Δ效应，则有：式中，M为墩柱底的弯矩；F为墩柱受到的水平作用力；L为墩高；P为上部结构产生的竖向荷载（等效集中作用于墩顶）。

另一方面，如图4所示，对于塑性铰区的截面，存在着如下近似的弯矩-曲率关系：

这样，可以联立式（12）、（13）和（14）来建立墩柱顶的水平作用力和位移之间的对应关系（即Pushover曲线）：

按前节介绍的Pushover分析步骤，需要将式（15）中的Pushover曲线转化为能力谱曲线。对于这样的简化情况，有：

式中，g为重力加速度。

式（15）和式（16）建立了独立混凝土墩柱的能力谱曲线，其表达的形式简单，而且避免了有限元软件建模分析的麻烦。

如果给出了墩柱精确的M-φ曲线，则可以按照如下方法来得到Pushover曲线：给定曲率值φ，然后由式（12）计算得到Δ（ϕ），再由M-φ曲线给出弯矩M，进而由式（13）解出F。从这里也可以看到，Pushover曲线可以由M-φ曲线通过线性变换得到。

如果考虑墩柱顶的支座刚度，如图5所示，则可按如下方法来得到Pushover曲线。

更为一般地，如果某一联桥有多个墩柱，则可以先分别得到每个墩柱的Pushover曲线，然后将这些曲线线性叠加，即可得到整联的F-Δ曲线。

对于规则圆形或矩形的墩柱截面，由规范可以直接算得M-φ曲线的关键参数，从而方便地得到Pushover曲线（中华人民共和国行业标准，2008）；而对于复杂、不规则的截面，可以通过迭代算法（叶列平，2005）给出其M-φ曲线。

3 算例分析

算例引用康钊（2005）对官园桥5号轴桥墩进行顺桥向Pushover分析的结果，以该文献中的计算结果与本文方法给出的结果进行对比。

考虑的桥墩为门式双墩柱–盖梁结构，墩柱尺寸如图6所示，柱高为5m。抗震设防烈度为8度，设计基本地震加速度为0.20g，场地类别为II类。考虑如图7所示的模型，其中用弹簧模拟支座，其水平抗推刚度为K=45481kN/m。

塑性铰长度Lp（cm）由规范给出（中华人民共和国行业标准，2008）。

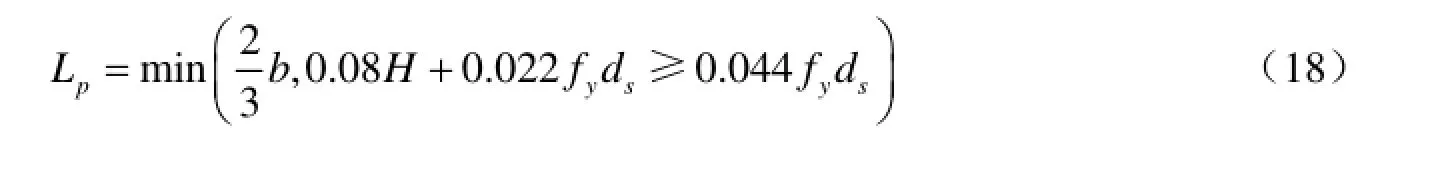
图5 考虑支座水平位移的Pushover分析Fig. 5 Pushover analysis considering the horizontal displacement of bearing

图6 墩柱的截面尺寸Fig. 6 Section size of the Guanyuanqiao abutment at Beijing

图7 Pushover计算模型Fig. 7 Pushover analysis model

其中，b为矩形截面的短边；H为塑性铰截面到反弯点的距离（cm）；fy为纵向钢筋抗拉强度标准值（MPa）；ds为纵向钢筋的直径（cm）。

康钊（2005）给出了墩柱潜在塑性铰区截面的弯矩-曲率曲线，如图8所示。由此M-φ曲线，结合本文的方法，则可以得到Pushover曲线，如图9所示。

图8 单个墩柱的弯矩-曲率曲线Fig. 8 Moment-curvature curve for single abutment

图9 Pushover分析结果Fig. 9 Result of the Pushover analysis

为了对结构进行抗震性能分析，将Pushover曲线转化为能力谱曲线，并与需求谱曲线画在同一坐标系中，如图10所示。

应注意图10中采用的是弹塑性反应谱。为了考虑结构的弹塑性，Vidic等（1994）提出用折减系数R(μ)来对弹性反应谱进行修正：

其中，μ为位移延性系数（秦泗凤，2008），由式（9）和式（11）可得：

R(μ)与μ的关系可表示为：

其中，Tg为结构的特征周期；c1，c2，cR和cT由结构的滞回性质确定，取值见表1。

表1 取ξ = 0.05时，式（21）中的参数取值Table 1 Values for parameters in equation (21) when ξ=0.05

在图10中从康钊（2005）的结果和本文方法给出的结果均能看到，在8度设防烈度E2地震作用下，支座顶的水平位移为60mm，墩顶的水平位移约为30mm，为墩柱高度的1/167，满足变形控制要求。同时，从图10中也可以看到，用本文方法得到的近似Pushover分析方法与非简化情况相比，二者给出的结果符合的很好。

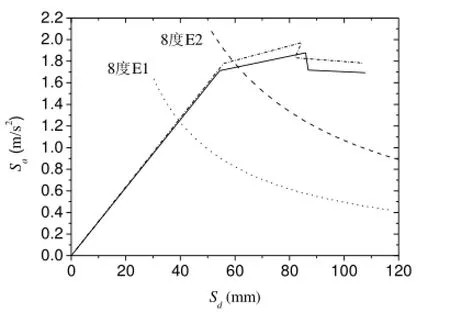
图10 确定结构的性能点Fig. 10 Determination of the performance point

4 结论

本文主要讨论了简支梁桥的简化Pushover分析方法。对于非高墩桥梁，由于结构重力主要来自于上部结构，故而可以将之简化为单自由度体系。在给定截面的弯矩-曲率曲线后，则通过简单的运算即可得到结构Pushover曲线，从而省去了有限元建模的麻烦。算例分析结果表明，该方法的精度满足工程要求，从而对工程运用有一定的参考价值。

康钊，2005．北京市在用市政桥梁基于位移的抗震安全评估（硕士学位论文）．清华大学.

刘晶波，杜修力，2005．结构动力学．北京：机械工业出版社．

马千里，叶列平，陆新征，2008．MPA法与Pushover法的准确性对比．华南理工大学学报（自然科学版），36（11）：121—128.

毛建猛，2008．Pushover分析方法的改进研究（博士学位论文）．中国地震局工程力学研究所.

秦泗凤，2008．桥梁抗震性能评价的静力非线性分析方法研究（博士学位论文）．大连理工大学.

叶列平，2005．混凝土结构（上册）．北京：清华大学出版社.

中华人民共和国行业标准，2008．公路桥梁抗震设计细则（JTG/T B02-01-2008）．北京：人民交通出版社.

中华人民共和国国家标准，2001．建筑结构抗震设计规范（GB 50011-2001）．北京：中国建筑工业出版社.

Chopra A.K.，Goel R.K.，2000．Evaluation of NSP to estimate seismic deformation：SDF systems．Journal of Structural Engineering，126（4）：482—490.

Chopra A.K.，Goel R.K.，2002．A modal pushover analysis procedure for estimating seismic demands for buildings．Earthquake Engineering & Structural Dynamics，31（3）：561—582.

Fajfar P.，Gašperšič P.，1996．The N2 method for the seismic damage analysis of RC buildings．Earthquake Engineering & Structural Dynamics，25（1）：31—46.

FEMA 273，1996．NEHRP commentary on the guidelines for the rehabilitation of buildings．Washington，D.C.：Federal Emergency Management Agency.

Gupta B.，Kunnath S.K.，2000．Adaptive spectra-based pushover procedure for seismic evaluation of structures．Earthquake Spectra，16（2）：367—392.

Vidic T.，Fajfar P.，Fischinger M.，1994．Consistent inelastic design spectra：strength and displacement．Earthquake Engineering & Structural Dynamics，23（5）：507—521.

Simplified Pushover Analysis Method for Simply Supported Concrete Bridges

Wang Cao1), Bao Qiwei2)and Li Quanwang1)

1) Department of Civil Engineering, Tsinghua University, Beijing 100084, China
2) Beijing General Municipal Engineering Design and Research Institute, Beijing 100035, China

The Nonlinear Static Pushover analysis is a method utilized for description of the structural seismic performance under strong earthquakes, and it has been widely used by many researchers. This paper mainly discusses the simplified Pushover method for simply supported concrete bridges. It is noted that for regular bridges with short piers, the structural weight comes mainly from the superstructure, with which the analytical model can be simplified as a single degree system. The Pushover curve can be obtained with simple algebra given the moment –curvature relationship of the section in the potential hinge area, indicating that one does not need to establish a finite element model to get the Pushover curve. Thus, the proposed method can be a valuable reference for practice. Finally, the accuracy of the simplified method is presented with an illustrative example.

Simply supported concrete bridges; Pushover analysis; Seismic safety assessment; Simplified method

王草，包琦玮，李全旺，2014．简支混凝土梁桥Pushover分析简化方法．震灾防御技术，9（3）：439—446．

10.11899/zzfy20140310

清华大学自主科研基金（20121087910）

2014-03-11

王草，男，生于1993年。硕士研究生。主要从事桥梁安全评估工作。Email：mornsun17@gmail.com