含DG的馈线电压分布特性仿真实验设计
2014-05-02孙秋野
梁 雪,孙秋野,贾 旭,张 羽
(东北大学 信息科学与工程学院,辽宁 沈阳 110819)
目前,世界范围内的电力系统仍以集中发电方式为主。但是,随着集中式发电的种种弊端日益凸显,各国能源专家逐渐把研究的目光投向了具有小型、分散、灵活、靠近负荷和合理利用清洁能源等特点的分布式发电方式。
分布式发电(distributed generation,DG)是一种利用各种分散存在且可用的能源(包括可再生能源,如小型风能、水能和太阳能等)进行发电供能的技术[1]。在馈电线路上接入DG,线路的电压分布将会发生变化,这与DG的接入位置、网络的拓扑结构和负荷量的相对大小等因素有关[2]。为使学生能够通过实验了解到DG的接入对于馈线乃至于整个配电网的影响,需要开发一种馈线上有DG接入情形的仿真实验。
1 研究馈线电压特性的理论基础
1.1 负荷模型
要了解DG对于馈线电压的影响,首先要建立馈线电压分布的数学模型,在此仅以负荷沿馈线均匀分布的模型为例进行建模。
所谓负荷沿馈线均匀分布,就是指线路上各点的负荷都相等。因为实际系统中不可能保证负荷完全符合均匀分布,所以只能将负荷的分布近似看作是均匀的[3]。图1为第ω条含DG的负荷近似均匀分布的馈线示意图,图中曲线为实际的负荷分布情况,M和N分别表示线路的始端和末端,k1,k2,… ,kn为分布式电源的接入点。始端M处的负荷功率为P0+jQ0,其中P0为负荷的有功功率,Q0为负荷的无功功率,dω为第ω条线路上的任意位置。
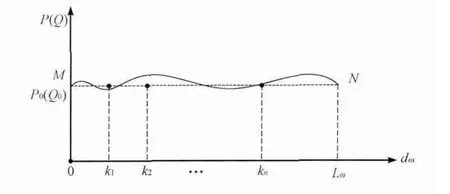
图1 含DG的负荷近似均匀分布的配电线路
为方便起见,这里直接给出负荷均匀分布的模型:n个容量分别为PDGi+jQDGi的DG布置于第ω条线路的k1,k2,…,kn处,k1,k2,…,kn∈[0,Lω]。设k0=0,kn+1=Lω,当第ω条馈线上任意一点dω∈[ki-1,ki](i=1,2,…,n+1)时,dω点前后的负荷分布为:
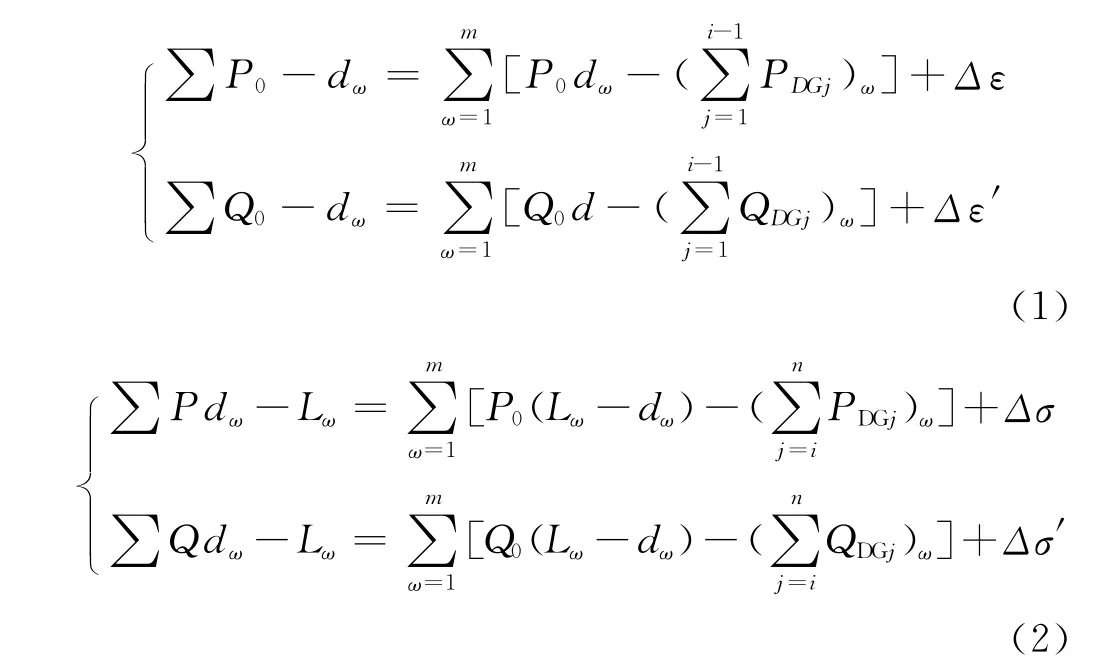
1.2 馈线电压分布模型
为了方便研究,这里仅推导单支馈线的电压分布表达式,即式(1)和式(2)推导结果中的求和部分去掉,令m=1,同时去掉各式的小角标ω,并忽略因负荷分布的不均匀性而产生的Δε、Δσ、Δε′和Δσ′。设馈电线路的额定电压为uN,那么线路上任意一点d处的电压被定义为:
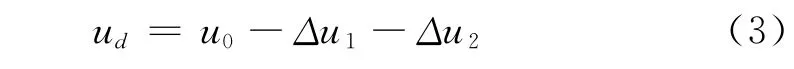
式中u0表示线路始端的电压,Δu1表示因d点之后的等效综合负荷而引起的压降,Δu2表示因d点之前的负荷而引起的压降[4-6]。
当馈线上接入一个容量为PDG+jQDG的DG,单位长度的线路阻抗表示为z=r+jx,这里注入容量给定的是一个复功率[7]的形式,在计算压降时要按照复功率的定义求取线路的电流。在以往对于电压降的研究中,为了计算简便,都将电压降落的横分量去掉,仅保留纵分量来近似表达电压降的情况[8]。这里,为了更真实地反映DG对负荷模型电压分布的影响,将同时考虑电压降的横分量和纵分量,即所推导的电压分布表达式是含有虚部的。这里直接给出推导之后的电压分布模型。
在未接入DG时,负荷均匀分布模型的馈线电压解析表达式为:
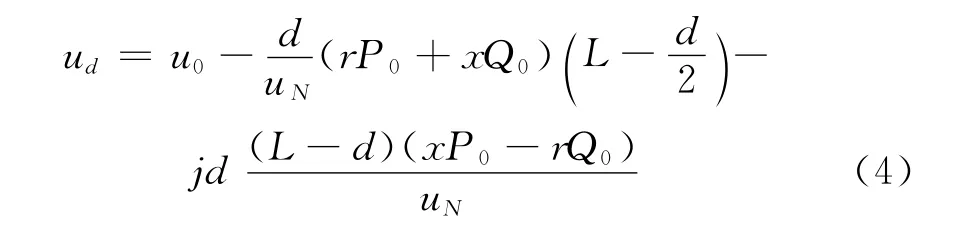
含有n个DG时(n个DG布置于线路的k1,k2,…,kn处,k1,k2,…,kn∈[0,L]),假设k0=0,kn+1=L。当d∈[ki-1,ki](i=1,2,…,n+1)时,含有n个DG的含虚部的馈线电压分布表达式为:
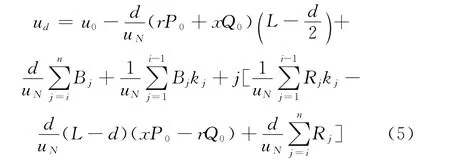
其中Bj=rPDGj+xQDGj,Rj=xPDGj-rQDGj,它体现了线路电压分布与DG容量有很大关系。
2 DG对馈线电压的影响分析
由式(4)和式(5)可知,DG的接入,使馈线电压的解析式发生了改变,根据式(5)可以分析出,馈线电压的分布与DG的接入数量(即n)、接入位置(即ki)和注入容量(即PDGi+jQDGi)有关,要通过仿真实验具体分析DG的接入数量、接入位置和注入容量对馈电电压的影响。合理的安装配置方式可以有效地改善配电网的供电质量并减小网损;反之,将对电网的安全、稳定运行造成消极的影响。
3 实验设计与结果分析
因电压的分布与DG的接入数量、接入位置和注入容量有关,这里将设计3组实验来分别验证DG电压对于馈线电压分布的影响,仿真实验采用Matlab软件[9-12],仿真参数如下:
馈电线路始端电压u0=10.5kV,额定电压uN=10kV,线路总长度L=15km,单位长度的线路电阻r=0.3Ω/km,电抗x=0.6Ω/km,线路始端的有功负荷P0=0.4MW,无功负荷Q0=0.2Mvar。
3.1 DG数量对电压影响的研究
3.1.1 实验过程
本文仅考虑DG数量对馈线电压的影响,因此必须排除DG的接入位置和注入容量对馈线电压的影响。方法是:无论接入的DG数量是多少,均把这些DG安置在线路的等分点处,以排除接入位置的影响;无论接入的DG数量是多少,固定其总的出力情况,即这些DG的总容量是相同的,以排除注入容量的影响。
表1为DG数量、位置和容量的相关信息,并以此表为依据,进行仿真实验。

表1 DG数量、位置和容量信息
表1只给出了DG的有功注入容量。为方便研究,这里取DG的功率因数为cosθ=1,即此时DG的无功注入容量为0(下文均如此)。在馈线7.5km处接入一个DG时的仿真结果如图2所示,在馈线的3 km、6km、9km和12km处各接入一个DG时的仿真结果如图3所示。
3.1.2 结果分析
根据仿真结果,可以得出以下结论:在DG的接入点处,馈线电压存在波动的情况,DG的接入会整体抬高馈线的电压。随着DG接入数量的增多,馈线电压的走势更加稳定和平滑,在馈线接入点处体现得尤为明显。在DG总的注入容量一定的情况下,将总容量分散布置于线路上多个点,会比将全部容量集中于馈线上某一点或较少点时,得到更加理想的电压分布。

图2 接入1个DG的馈线电压分布
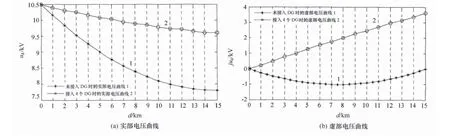
图3 接入4个DG的馈线电压分布
3.2 DG接入位置对电压影响的研究
3.2.1 实验过程
这里仅考虑DG的接入位置对馈线电压的影响,因此必须排除DG的数量及注入容量对馈线电压的影响。采用的方法是:统一接入双DG以排除DG数量对馈线电压的影响;DG的总容量固定不变,以排除DG注入容量对馈线电压的影响。以表2为依据,进行仿真实验。

表2 DG位置和容量的信息
在馈线3km和5km处接入DG时的仿真结果如图4所示,在馈线9km和11km处接入DG时的仿真结果如图5所示。
3.2.2 结果分析
根据仿真结果,可以得出以下结论:如果DG的接入位置靠近线路的始端,对电压有一定的抬高作用,但是影响较小;当DG的接入位置由线路的始端向中间部位,再向线路的末端移动时,DG对于馈线电压的影响逐渐加大,即DG的接入位置越靠近线路的末端,对馈线电压的影响就越大;对于DG接入位置靠近线路末端的程度应该有一定的界限,否则将有可能出现某些节点的电压高于母线电压的情况(针对实部电压而言)。
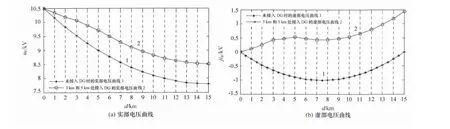
图4 在馈线3km和5km处接入DG的馈线电压分布
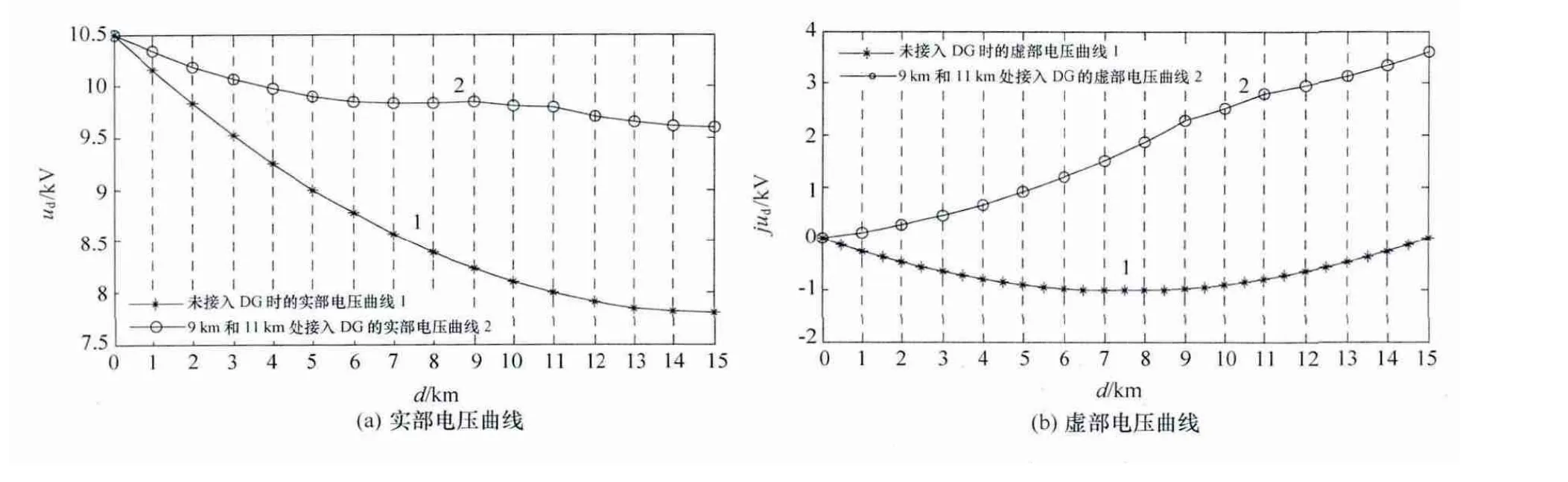
图5 在馈线9km和11km处接入DG的馈线电压分布
3.3 DG注入容量对电压影响的研究
3.3.1 实验过程
这里仅考虑DG的注入容量对于馈线电压的影响,因此必须排除其接入数量和位置对于电压的影响,采用的方法是:统一接入双DG以排除其数量对于馈线电压的影响;双DG的接入位置固定不变,以排除DG接入位置对馈线电压的影响。以表3为依据进行仿真实验。

表3 DG接入位置和注入容量的信息
图6为在馈线9km和11km处接入不同容量DG时的实部电压仿真结果。
图7为在馈线9km和11km处接入不同容量DG时的虚部电压仿真结果。
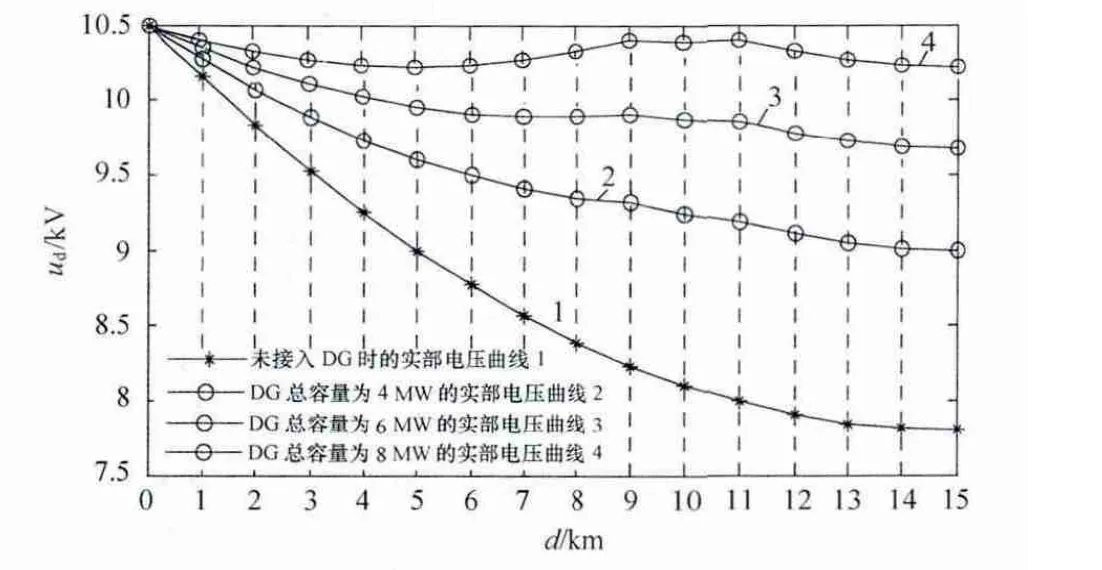
图6 不同容量的双DG下的馈线实部电压分布
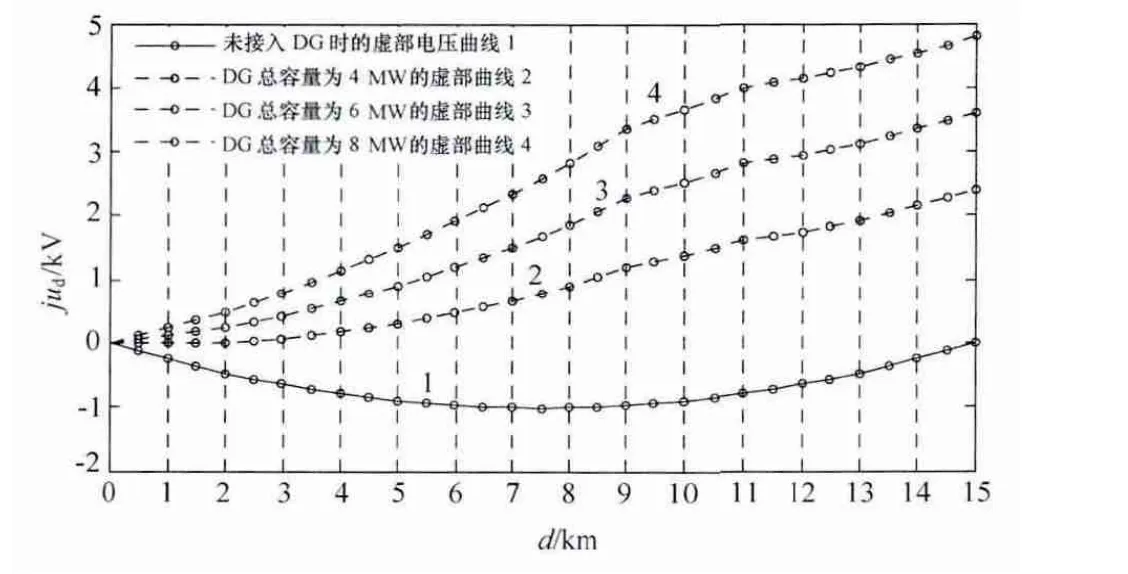
图7 不同容量的双DG下的馈线虚部电压分布
3.3.2 结果分析
根据仿真结果可以得出以下结论:DG的接入位置和数量一定时,DG对电压的支撑作用是与其注入容量成正相关;DG的注入容量应设有一定的上限,否则将有可能出现某些节点的电压高于母线电压的情况(针对实部电压而言)。
4 结论
在建立馈线电压分布模型的基础上,分别针对DG对馈线电压分布的3个影响因素进行了仿真分析,结论是:使用多DG将总容量分散于多点可以使馈线电压更为平滑和稳定,DG的接入位置越接近线路末端对馈线电压的影响越大,DG对电压的支持作用与其注入容量成正相关。实验结果可以使学生更容易理解DG的接入对配电网产生的影响。该结果为DG合理安装配置方式的确定提供了一定的理论依据。
(
)
[1]徐丙垠,李天友,薛永端,等.智能配电网讲座第二讲:分布式电源并网技术[J].供用电,2009,26(4):22-27.
[2]Aekerman T,Knyazkln V.Interaction between distributed generation and the distribution network [C]// Asia-Pacific:IEEE/IES Transmission and Distribution Conference and Exhibition.2002:1357-1362.
[3]李钟旭.配电网三相不平衡负荷调补控制系统的研究[D].沈阳:东北大学,2011.
[4]孙秋野,李钟旭,杨珺,等.分布式发电对配电网静态电压分布的影响[J].东北大学学报:自然科学版,2010,31(8):1074-1077.
[5]Li Zhongxu,Sun Qiuye,Xu Lili.Voltage profile of feeder with multiple distributed generators[C]//中国自动化学会智能自动化专业委员会,江苏省自动化学会.2009年中国智能自动化会议论文集:第三分册.2009:1145-1151.
[6]Sun Qiuye,Li Zhongxu,Yang Jun,et al.Load distribution model and voltage static profile of Smart Grid [J].Journal of Central South University of Technology,2010,17(4):824-829.
[7]王文辉,刘淑英,蔡胜乐.电路与电子学[M].北京:电子工业出版社,2005.
[8]韩祯祥.电力系统分析[M].杭州:浙江大学出版社,2005.
[9]张化光,刘鑫蕊,孙秋野.Matlab/Simulink实用教程[M].北京:人民邮电出版社,2009.
[10]王晶,翁国庆,张有兵.电力系统的MATLAB/SIMULINK仿真应用[M].西安:西安电子科技大学出版社,2008.
[11]薛定宇,陈阳泉.高等应用数学问题的MATLAB求解[M].北京:清华大学出版社,2008.
[12]李维波.MATLAB在电气工程中的应用[M].北京:中国电力出版社,2007.
