基于扭转振动装置的内模PID控制器设计

王佳伟，杨亚非，2，钱玉恒

（1.哈尔滨工业大学 飞行器控制实验教学中心，黑龙江 哈尔滨 150001；2.哈尔滨工业大学 控制与仿真中心，黑龙江 哈尔滨 150080）

美国ECP公司生产的Model205a型扭转振动装置是一个高性能的多功能平台，通过不同的配置方式，可以推广到实际系统，例如机床［1］、汽车［2－3］等系统的控制性能研究，可以模拟存在耦合作用的离散振动系统，比如航天器上的太阳能帆板［4－5］，以及汽车的发动机曲轴系的扭转振动［6－9］，还可以模拟船舶轴系系统［10－12］和带有干扰的系统。在构建控制对象的数学模型时，可以按照研究的需要，容易将其建模为二阶、四阶或六阶控制对象。本文将其配置为一个二阶的弹簧质量振荡器的结构，推导了该对象的数学模型，设计了内模PID控制器，并且通过实验仿真验证了控制器的作用效果。通过该装置，学生可以掌握扭转振动实验装置的结构组成和使用方法，同时可以了解内模PID控制器的优势和设计过程，为进一步学习先进的控制算法打下基础。

1 扭转振动装置

该实验装置由图1所示的机电部分、控制系统和执行程序3个子系统组成，比较详细的介绍见参考文献［13］。

2 刚体对象的模型推导

实验装置可配置为经典的弹簧质量振荡器（忽略摩擦），如图2所示，输入为转矩T（t），输出为圆盘的角度θ（t），圆盘的惯量为J，k为弹簧劲度系数。

根据圆盘受力分析及牛顿第二定律的旋转形式得到运动方程为

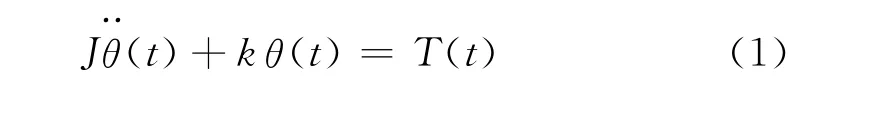
图1 扭转振动装置组成图

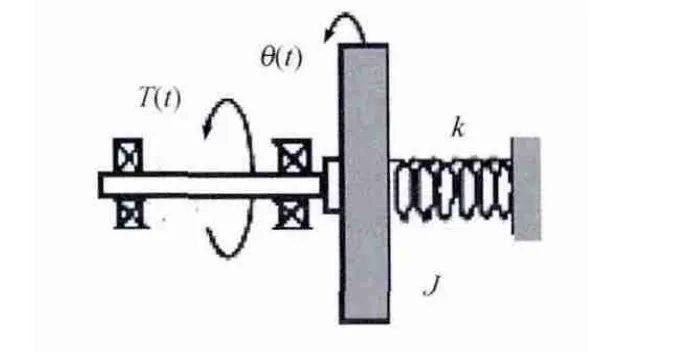
图2 弹簧质量振荡器

对上式两边取拉普拉斯变换，并假设初始条件为零，得到传递函数为

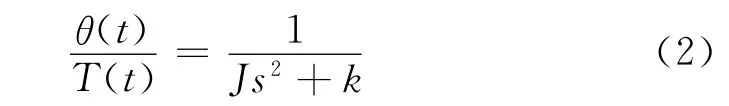
通过传递函数可知，该模型为一个经典的单自由度弹簧质量振荡器，是二阶系统，可以模拟单自由度对象中存在扭转振动时的特性。对于该模型的进行控制算法的研究，具有重要的应用意义。

3 内模PID控制器的设计及仿真验证

内模控制是一种基于过程的数学模型进行控制器设计的先进控制算法。其设计简单，控制性能良好，在系统分析方面的具有优越性，并且为研究预测控制等基于模型的控制策略提供了重要理论基础。内模控制在系统稳定性和鲁棒性理论分析方面具有优势，因此将内模控制原理与经典PID控制器相结合，可以显著提高PID控制器的鲁棒性能。同时与经典PID控制相比，内模PID控制器仅有1个整定参数，参数调整与系统动态品质和鲁棒性的关系比较明确。由于篇幅所限，本节简单介绍内模PID控制器的设计方法和步骤，略去详细的证明和推导（有兴趣的读者可参考文献［14］），然后针对扭转振动装置来验证内模PID方法的有效性。

3.1 内模PID控制器的设计

3.1.1 内模控制器的结构

如图3所示，图中GIMC（s）表示内模控制器的传递函数，（s）表示对象或者过程的数学模型，GC（s）表示等价控制器的传递函数，GP表示实际的对象或者过程的传递函数。

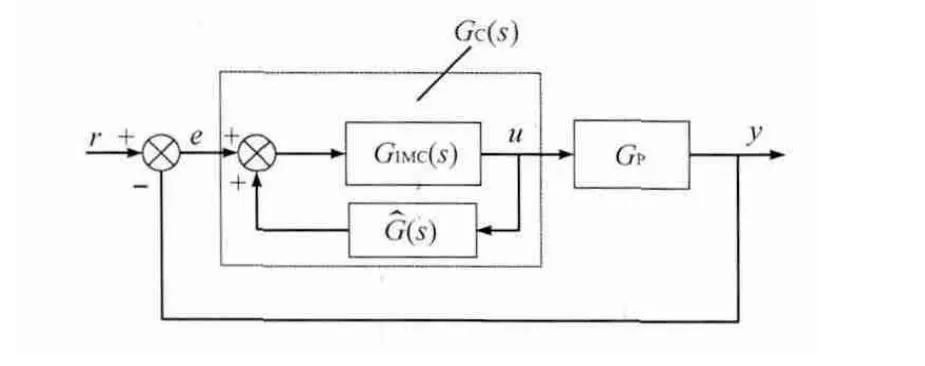
图3 内模控制结构框图

3.1.2 内模控制器的设计方法和步骤

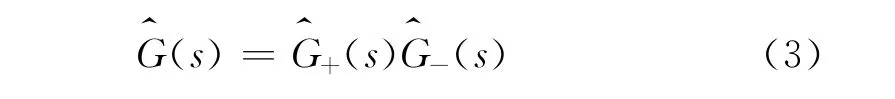
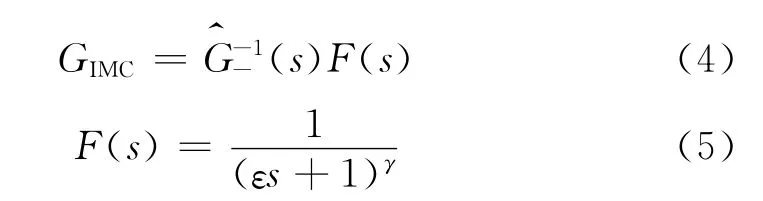
考虑对象模型的正反馈，进而得到等价的控制结构如图4所示。GC（s）为等价控制器的传递函数。

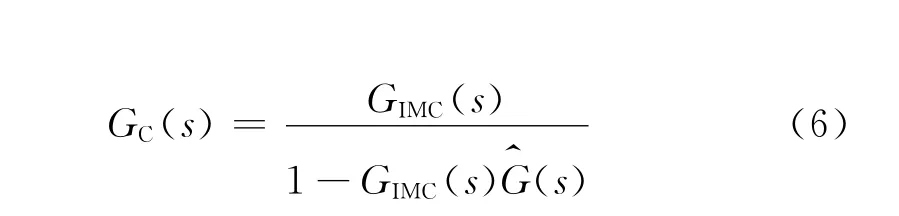
内模PID控制器的设计思路为：按照上面的步骤设计内模控制器，得到等价控制器的GC（s），然后等效地将GC（s）转化为传统PID控制器的结构，就得到基于内模控制的PID控制器的传递函数。GIMC＋PID（s）即为内模PID控制器的传递函数。内膜PID控制器的结构框图见图5。

控制器各参数的推导过程如下：

将公式（5）代入公式（4），得

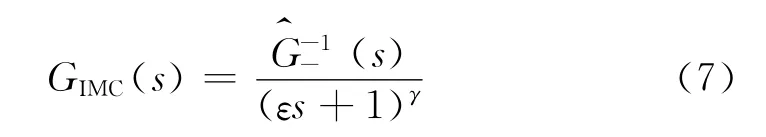
再将式（7）代入式（6），得

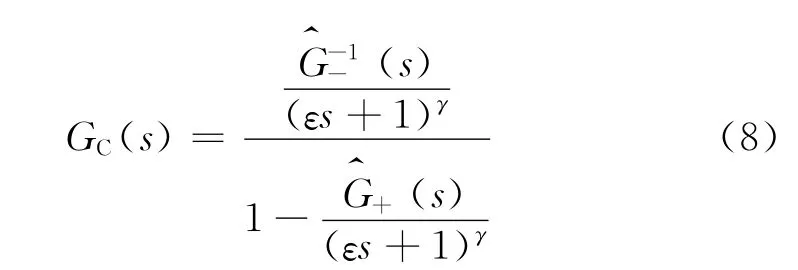
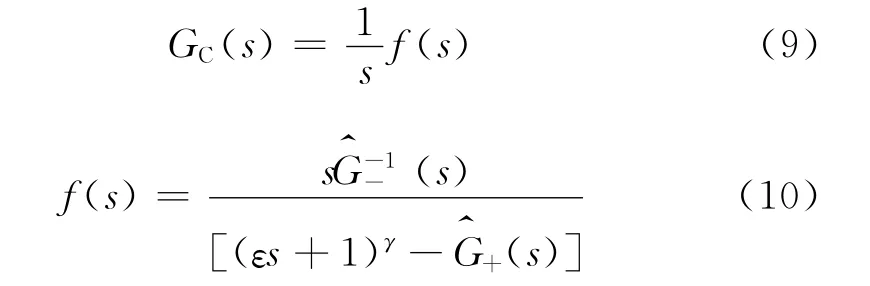
理想PID控制器的传递函数为

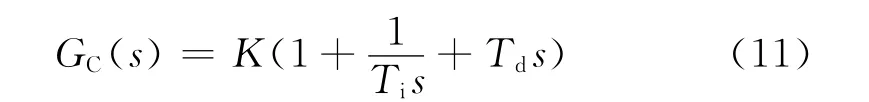
将f（s）进行泰勒级数展开，可以得到

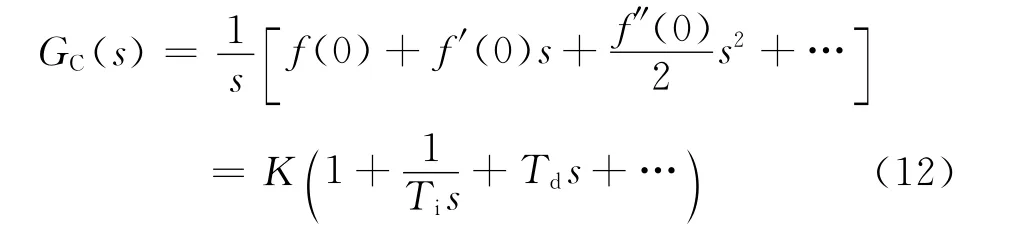
得到

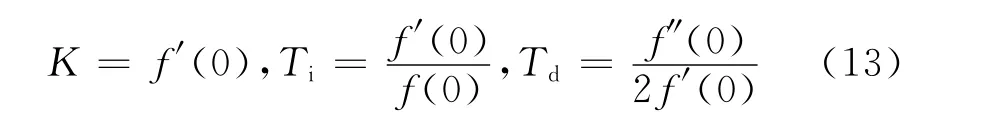
上面的公式可以用来求取控制器的增益、积分时间和微分时间，这些参数是过程模型参数和IMC滤波器时间常数的函数，如果过程的模型参数确定，则P、I、D参数只与IMC滤波器时间常数有关。

3.2 扭转振动装置的控制器参数的设计

以扭转振动装置作为被控对象，来实施内模PID控制器的设计。

扭转振动装置的数学模型为

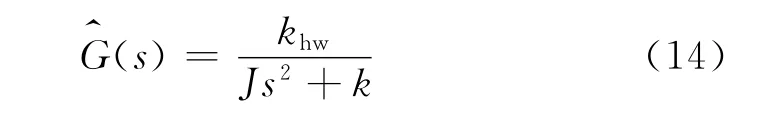
分解为两项：

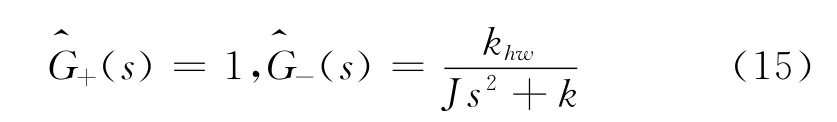
可得

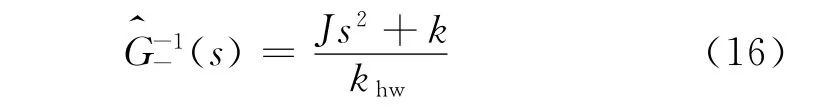
系统的阶次为2，故滤波器选择为

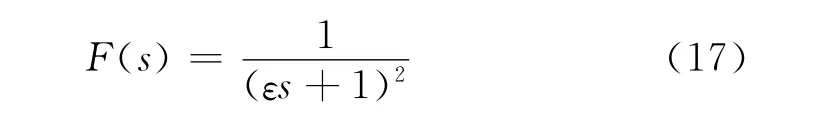
根据式（10）得到

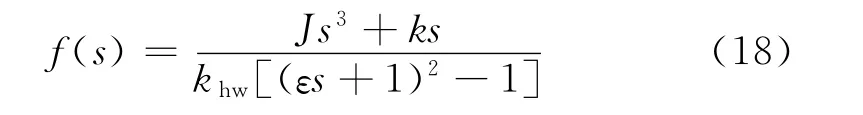
则等价控制器有

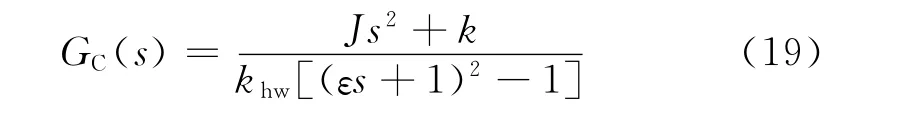
对控制器进行泰勒级数分解，即可得到内模PID控制器的参数如下：

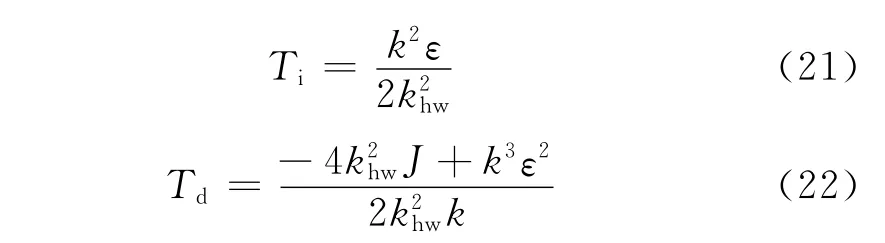
khw表示装置的硬件增益，计算公式为

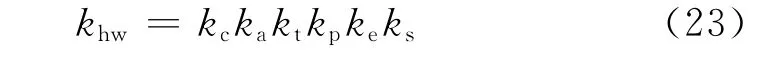
其中：kc代表DAC增益，ka代表伺服放大增益，kt代表伺服电机转矩常数，kp代表驱动滑轮比，ke代表编码器增益，ks代表控制器软件增益。J表示圆盘的转动惯量，k表示弹簧劲度系数。

3.3 仿真验证

通过系统辨识的实验，可以确定khw，J，k的值。通过ε的不同取值，即可改变PID的参数。令ε＝0.5和ε＝1时，计算得到相应的PID参数。

内模PID控制器仿真步骤包括：设置输入幅值为2 500、持续时间为2s、重复次数为1的阶跃信号；选择控制器类型为PID，分别输入两种ε数值下的控制器参数，并加载到控制器中，设置数据采集，绘制仿真图形。得到对象的阶跃响应曲线见图6和图7。

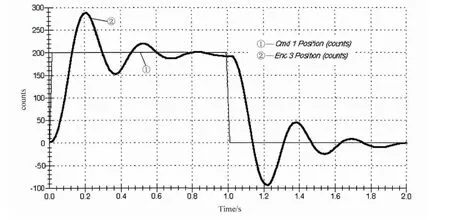
图6 ε＝0.5的内模PID控制器阶跃响应曲线

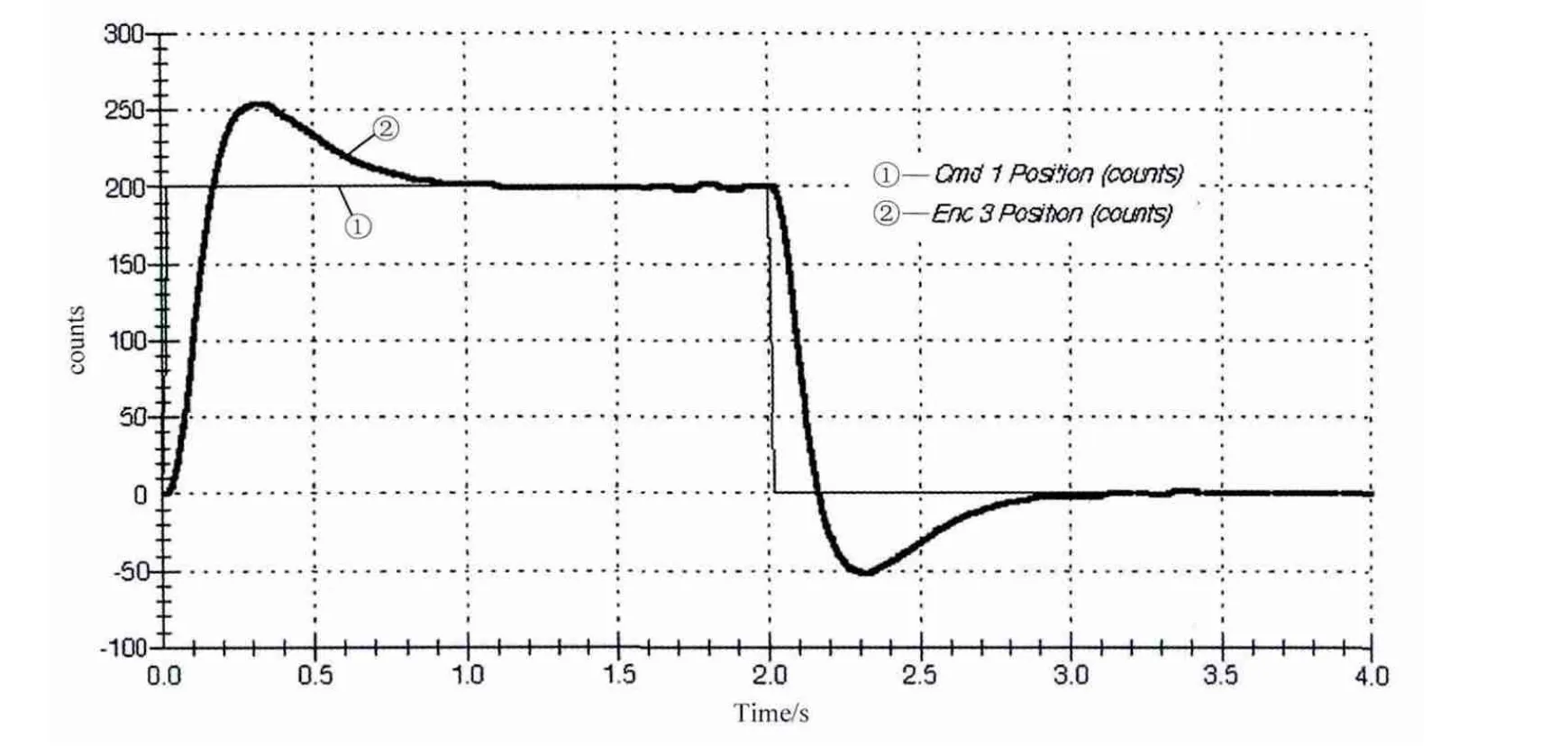
图7 ε＝1的内模PID控制器阶跃响应曲线

由两种情况的响应曲线可知，针对扭转振动装置这个被控对象，ε取较大数值时的控制效果较好。

4 结论

本文对美国ECP公司的扭转振动装置的系统组成、性能和所能实现的功能进行概要介绍，该套系统的整体性能优异，和目前其他类型的扭转振动系统差别很大。在实验过程中充分掌握实验装置的操作方法，加深对所学典型控制系统设计方法的理解，为学生进一步学习控制方法打下基础。

（

）

［1］Raub J，Jones J，Kley P，et al.Analytical Investigation of Crankshaft Dynamics as a Virtual Engine Module［G］.SAE Technical Paper，1999.

［2］杜极生.轴系扭转振动的试验监测和仪器［M］.南京：东南大学出版社，1995：75－96.

［3］何渝生.汽车振动学［M］.北京：人民交通出版社，1990：76－141.

［4］Bagci C A.Computer Method for Computing Torsional Nature Frequencies of Nonuniform Shafts Geared System，and Curved Assemblies［C］／／Proceedings of the 3rd OSU Mechanical Conference.O－klahoma，1973，40：1－15.

［5］Carrato P J，Fu C C.Model Analysis Techniques for Torsional Vibration of Diesel Crankshaft［M］.USA：SAE，1986.

［6］徐兀.汽车振动和噪声控制［M］.北京：人民交通出版社，1987：54－72.

［7］吕兴才.内燃机轴系扭转／弯曲／纵向振动的研究与控制［D］.天津：天津大学，2001.

［8］李震，桂长林，孙军.内燃机曲轴轴系振动分析研究的现状、讨论与展望［J］.内燃机学，2002，20（5）：469－473.

［9］王才峰.内燃机曲轴系扭振的多体动力学分析［D］.杭州：浙江大学，2006.

［10］徐敏，骆振黄，严济宽，等.船舶动力机械的振动、冲击与测量［M］.北京：国防工业出版社，1981：36－52.

［11］张洪田，王传溥.船舶轴系合理校中计算的Ricctai传递矩阵法［J］.船舶工程，1992（1）：26－31.

［12］张洪田，汤儒涛.船舶轴系扭转振动计算的Riccati传递矩阵法［J］.船舶工程，1994（1）：31－35.

［13］王佳伟，杨亚非，钱玉恒.基于扭转振动装置的PID实验设计［J］.2014，31（3）：59－62.

［14］李敏.鲁棒PID控制器的设计及应用［D］.合肥：中国科学技术大学，2004.