超分辨率复原方法相关原理研究

2014-04-30高慧斌王伟国张振东

中国光学 2014年6期

关键词：低分辨率高分辨率复原

陈健,高慧斌,王伟国,张振东,路明

(1.中国科学院长春光学精密机械与物理研究所,吉林长春 130033；2.中国科学院大学,北京 100049；3.吉林大学通信工程学院,吉林长春 130012)

超分辨率复原方法相关原理研究

陈健1,2,3,*,高慧斌1,王伟国1,张振东1,路明1

(1.中国科学院长春光学精密机械与物理研究所,吉林长春 130033；2.中国科学院大学,北京 100049；3.吉林大学通信工程学院,吉林长春 130012)

介绍了超分辨率复原方法的概念和理论基础；重点总结了常用的超分辨率复原方法，并对相关的理论依据、优缺点和适用范围进行了详尽分析；对超分辨率复原方法的未来发展进行了展望。超分辨率复原方法分为频域法和空域法。频域复原法原理简单清楚，计算方便，但是所建立的运动模型都是平移模型，不具有一般性，同时难以利用正则化约束，因而导致难以使用图像的先验信息进行超分辨率复原。空域复原法可以很方便地建立复杂的运动模型，同时考虑了几乎所有的图像降质因素，例如噪声、降采样、由非零孔径时间造成的模糊、光学系统降质和运动模糊等，还可以加入更完善的先验知识，相比于频域复原法，空域超分辨率复原模型更符合实际的图像退化过程，是目前应用最广泛的一类超分辨率复原方法。

超分辨率复原；频域法；空域法；凸集投影约束

1 引言

“超分辨率”一词的定义，经历了一系列的发展过程。成像系统可以看作是一个低通滤波器，经历了降采样和低通滤波的过程，原始图像中的一些高频信息被滤除掉了，所成的图像不是十分清晰。传统的图像复原方法只能在系统的极限衍射频率范围内去估计图像信息，无法突破硬件条件的限制，为此超分辨率复原方法应运而生。最初学者们认为超分辨率复原方法指的就是估计超过成像系统衍射极限范围的图像信息的复原方法。随后，学者们发现对同一个场景所成的图像序列包含的信息是不尽相同的，结合这些低分辨率图像序列，采用图像处理的方法就可以获得视觉效果较好的高分辨率图像。随着超分辨率方法的进一步发展，超分辨率复原方法将越来越多的图像降质因素考虑在内，包括序列图像的亚像素位移、红外相机的动态响应范围、成像系统的固有噪声和图像的运动模糊等，越来越接近于实际的降质模型。

从图像处理角度，所谓的超分辨率复原，就是利用一幅或者多幅低分辨率的图像，结合特定的方法，来估计频率信息大于光学成像系统截止频率的高分辨率图像的过程，该过程主要克服的困难有光学系统的像差、大气扰动和目标与光学系统之间的相对运动产生的模糊、成像系统噪声、红外相机降采样丢失的信息和光学系统离焦等。超分辨率复原是图像融合的一个分支，同样是一个病态问题，也就是说输入图像参数的轻微扰动都会导致估计图像产生较大的偏差，学者们一直都在致力于解决这个问题。

目前，超分辨率复原已经应用于多个领域，也已经成为图像配准方面发展比较活跃的一个分支。例如法国的SPOT和美国的EarthSat公司已经成功地将超分辨率复原技术应用于商业领域，在卫星图像复原中取得较好的效果。

2 超分辨率复原方法中的图像退化模型

要研究超分辨率复原方法，首先必须了解图像退化的机理，也就是低分辨率降质图像的成因，建立合适的降质模型。如果将质模型建立的足够精确，那么根据其逆过程则可以很容易地恢复出高质量地高分辨率图像。

自然图像可以看作是一个在所有频段都有分量的连续信号，由于发生几何形变和运动模糊，经过光学系统降采样后离散化，加上前面分析的加性噪声，最后形成了降质图像。由同一光学系统对同一场景采集的连续多帧图像序列，可以看作是自然原始图像经过不同的形变、模糊、降采样和噪声参数作用之后得到的不同图像。在传统的图像复原过程中，考虑的一般只有运动模糊和加性噪声，而超分辨率复原过程中考虑的因素显然更多。在成像系统中，只有光子散粒噪声是乘性的，这种小的噪声可以忽略，因此整个噪声模型可以用加性的高斯噪声近似得到。

根据考虑的主要退化因素不同，可以建立不同的退化模型。假设获得的低分辨率图像为｛lp1，lp2，…，lpn｝，如果退化过程满足以下条件：几何形变为主要的退化因素；模糊原因不以相对运动为主，而是以光学系统的离焦、大气抖动为主要成因；几何形变发生在模糊之前。则建立基于形变的退化模型。

基于形变的图像退化模型如图1所示。

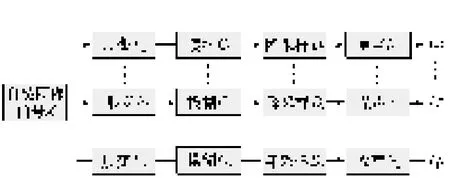
图1 基于形变的图像退化模型Fig.1 Image degradation model based on deformation

相应地，基于形变的图像退化模型的数学表达式如式(1)所示。

式中：为了计算和表示方便，假设自然图像场景的长宽比为1，尺寸为L×L，则X是一个L2×1的一维列向量，表示对自然图像进行行堆砌得到的矢量，Ci为L2×L2的系统模糊矩阵，Fi为L2×L2的几何形变矩阵，可描述各种几何变换如平移、旋转和尺度缩放等，Di为×L2的红外相机降采样矩阵，最后生成的低分辨率图像Lpi也是×1维的。

如果考虑运动模糊为主要的退化因素，或者模糊过程发生在形变过程之前，则建立基于运动模糊的退化模型。

基于运动模糊的图像退化模型如图2所示。

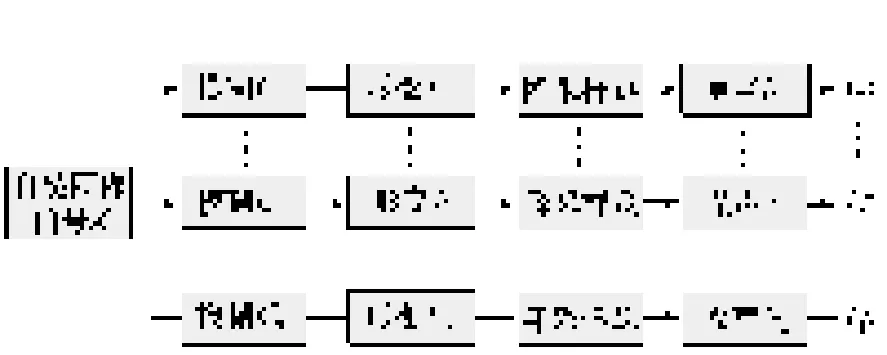
图2 基于运动模糊的图像退化模型Fig.2 Image degradation model based on motion blur

相应地，基于运动模糊的图像退化模型的数学表达式如式(2)所示。

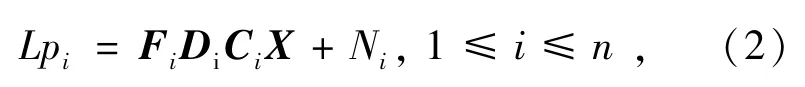
为了表示方便，也可以将式(1)和式(2)简单写为：

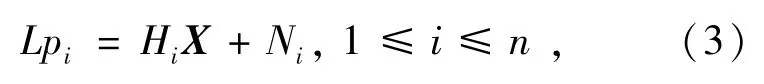
式中：Hi=DiFiCi或者Hi=FiDiCi，这便是所熟悉的经典图像退化模型。在上述模型中，大写字母表示的是信号的傅里叶变换。由式(1)、式(2)和式(3)可以得到一维列向量X如式(4)所示。

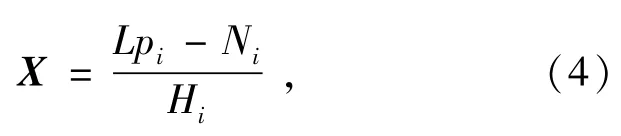
因为Hi是一个低通滤波器，高频部分趋于0，因此在高频上，Ni的一个细小的扰动都有可能导致X发生较大的变化，解空间不存在连续性。同时，较大的噪声容易导致观测到的低分辨率图像与高分辨率图像严重不符，无法进行估计。再者，在约束条件不同的情况下，得到的解也不尽相同。因此称超分辨率复原问题是一个病态问题。直接利用式(3)进行逆变换是不可行的，因为超分辨率复原的目的是恢复出超过光学系统截止频率的原始信号，这种直接进行逆变换得到的结果显然不可能超过光学系统的截止频率。

超分辨率复原的目标，就是研究如何从这一组低分辨率图像｛lp1，lp2，…，lpn｝中，找到原始图像信号X的近似估计。为了引出超分辨率复原模型的一些经典方法，下面首先介绍超分辨率复原的3个理论基础：信息叠加理论、解析延拓理论和非线性操作理论。

2.1 信息叠加理论

无论是可见光相机还是红外相机成像，采用的都是非相干成像机理，图像中不存在乘性相干斑噪声。同时，可以认为图像中的目标具有固定的大小。对于某一个目标信号f(x)，可以表示为：

式(5)中：rect(x/X)可以表示为：

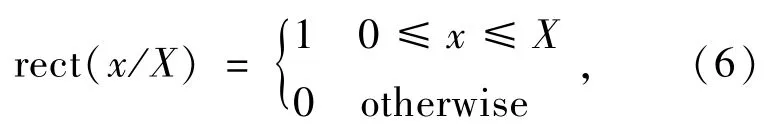
式(6)中：X表示目标的尺寸。式(5)表示在特定的范围内，目标是有信号的，而一旦超出了这个范围，目标信号就可以认为是0。光学系统相当于一个低通滤波器，假设其截止频率为Fc。对目标信号f(x)作傅里叶变换得到其频谱F(u)，假设其在截止频率之外和截止频率之内的频谱分别为Fa(u)和Fb(u)，则频谱F(u)可以表示为：

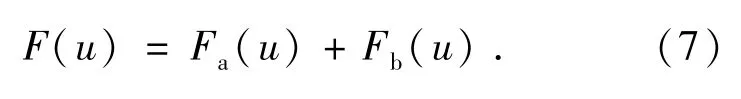
相应地，对式(5)作傅里叶变换，得到频谱F (u)可以表示为：

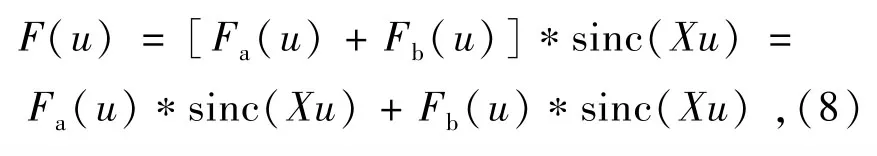
sinc(Xu)的频谱覆盖了整个频段，则式(8)中的Fa(u)*sinc(Xu)表示目标信号的低频分量会出现在光学系统截止频率以上，而Fb(u)* sinc(Xu)表示目标信号的高频分量会出现在光学系统的截止频率以下。也就是说，通过光学成像系统获得的低分辨率图像中，既包含目标的低频分量的信息，又包含目标高频分量的信息，如果能将所有这些频率信息都完整分离出来，就可以完全复原出高分辨率的目标图像。

2.2 解析延拓理论

解析延拓理论认为：一个解析函数一旦给定其在某一个连续区间上的值，则这个解析函数完全确定，换言之，不存在两个不同的解析函数，在某一区间上的取值处处相同。

根据上一小节的分析可知目标信号在空域有界，则其在频域上为解析函数。而根据式(2)可知从观测图像可以得到原始图像的低频分量(因为系统传递函数Hi是一个低通滤波器)，则根据低频区间的函数值，完全可以复原整个频域的傅里叶变换，这就是超分辨率复原的任务和目标。

2.3 非线性操作理论

根据式(2)可知，降质过程受到噪声影响，由此得到的式(4)中f(x)的估计值可能包含负数，或者不满足有界性。因此一般的图像复原均需要强制添加约束条件，对估计出的解进行截断，只保留满足有意义和非零的那部分解。截断是一个非线性操作，会对解附加高频分量，因此只要约束条件足够合理，便可以恢复出原始图像的高频分量，实现超分辨率复原。

本节论述了从观测到的低分辨率图像恢复高分辨率图像的可能性，下面着重介绍目前较为成熟的一些超分辨率复原方法。

3 常用的超分辨率复原方法分析

在超分辨率复原这个概念提出后的最初几年，学者们一般是使用单帧图像复原的方法，将其归为一般的图像复原问题，代表性的方法包括：基于解析延拓原理的外推法、基于长球函数的外推法、Papoulis-Gerchberg迭代法和一步外推法等。这类复原问题都是病态问题，观测误差和噪声的引入会对解产生很大影响，因此单帧图像复原法复原图像质量不能令人满意，难以应用在实际工程中，已逐渐淡出了人们的视野。

目前采用的超分辨率复原方法，基本上均使用了多帧的低分辨率图像，从不同图像中提取相互补充的信息，从而恢复出高分辨率图像［1］。多帧序列图像的超分辨率复原方法，一般可以分为图像配准、降晰参数辨识和复原3个步骤，因为利用到了丰富的信息和先验知识，所以复原效果优于单帧图像复原方法。基于多帧序列图像的超分辨率复原方法可以分为频域方法和空域方法，频域方法包括递归最小二乘法(Recursive Least Squares，RLS)、递归整体最小二乘法(Recursive Total Least Squares，RTLS)、消混叠复原法和广义采样定理法等，空域方法包括非均匀空间样本插值法、滤波器法、迭代反向投影法、代数滤波后向投影法、凸集投影(POCS)法、统计复原法和混合最大后验概率估算和凸集投影(MAP/POCS)法等，其中尤以空域复原方法使用最为广泛。

图3 超分辨率复原方法体系Fig.3 Methodology of super-resolution restoration

超分辨率复原方法体系见图3。

3.1 频域超分辨率复原方法

频域法的主要思想是假设序列图像之间存在位移变化，对序列图像首先进行傅里叶变换，并根据傅里叶变换的平移特性，消除序列图像之间的频谱混叠，获得更多原始图像的高频信息，从而得到高分辨率图像。频域法的基础是Tsai和Huang等提出的消混叠复原法，其余诸如RLS、WTLS和广义采样定理法都可以看作是对消混叠复原法的改进。

频域超分辨率复原方法的一般步骤如图4所示。

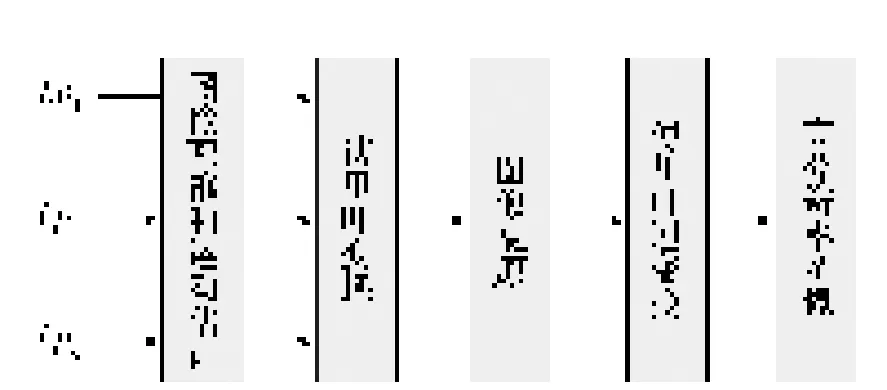
图4 频域超分辨率复原方法的一般步骤Fig.4 General steps of frequency domain super-resolution restoration

3.1.1 消混叠复原法

原始的高分辨率图像信号是二维连续信号，记为x(t1，t2)，它的傅里叶变换为X(w1，w2)。观测得到一系列低分辨率图像yk［n1，n2］，k=1，…，p是由这个信号经过平移和光学系统降采样得到的。假设第k个位移图像为：

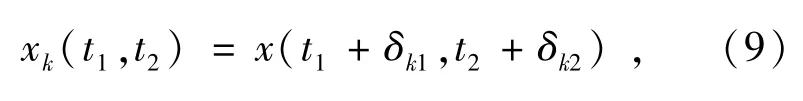
式(9)中：δk1和δk2为已知位移量，k=1，2，…，p。由傅里叶变换的位移性质，位移图像xk(t1，t2)的傅里叶变换如式(10)所示。

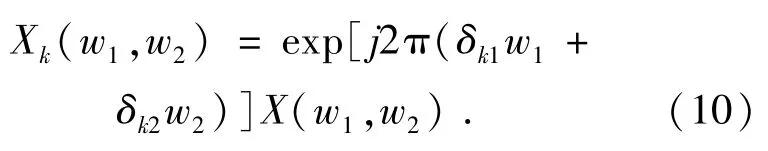
光学成像系统对位移图像xk(t1，t2)分别以T1和T2为周期进行离散采样，最终得到低分辨率图像序列yk［n1，n2］。根据傅里叶变换的频谱混叠性质，下式为：

式(11)可以简写为：

式(12)中：Y是p×1的列向量，第k个元素为yk［n1，n2］，X为L1L2×1的列向量，Φ是p×L1L2的变换矩阵。因为观测图像Y已知，平移关系可以通过图像配准方法得到，所以通过解上述方程组并经过傅里叶逆变换，就可以得到高分辨率图像。

消混叠复原法模型简单，实现起来也较为容易，但缺点是假设较为严格，只能处理序列图像之间是平移关系的情况，并且没有考虑光学系统的离焦、运动模糊和噪声等因素，实用性较差。

3.1.2 递归最小二乘法

Kim等［2-3］对传统的消混叠复原法进行了深入的研究，在复原过程中考虑了线性不变模糊、线性移变模糊和加性噪声等因素，将观测方程改写为更加复杂的形式，使用RLS和WRLS求解，并引入Tikhonov正则化方法，正则化方程如下：

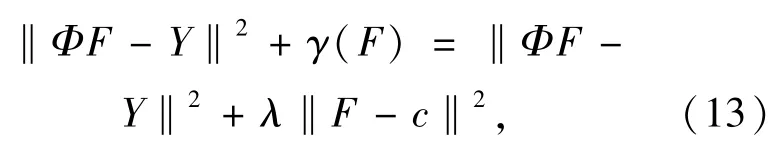
式(13)中：γ为正则化方程，c为解的估计值，γ为正则化系数。式(13)正则化方程的解如下：

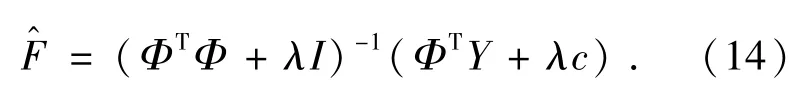
式(13)正则化方程可以通过最小二乘和递归最小二乘进行求解。

文献［4］对观测图像进行分块，重叠运动子块进行运动补偿，将消混叠复原法从整体运动模型推广到局部运动模型，使之具有一般性，但是只局限于平移运动，而没有推广到更加复杂的情况。

3.1.3 递归整体最小二乘法

考虑到由于模型系数的误差导致RLS求解对于某些系数可能不收敛的问题，文献［5］重新改写了文献［4］的方程组，并提出使用WRLS［6］进行求解(Weighted Recursive Least Squares，WRLS)的思路。

假设模型系数Φ的误差为EΦ，噪声的傅里叶变换为N，则观测模型可以改写为：

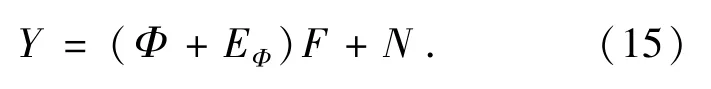
式(15)的方程可以使用递归整体最小二乘法进行求解。

3.1.4 广义采样定理法

广义采样定理法认为降质过程可以描述为一种线性退化模型，并将复原过程分为两个步骤，首先将不同的低分辨率图像信号合成，然后再对合成信号进行去模糊，该类方法的缺点是对所有的低分辨率图像都使用同一个点扩散函数(Point Spread Function，PSF)，并且图像之间的相对运动还是局限于平移。

综上所述，频域法的优点包括：原理简单清楚，大多数是基于离散傅里叶变换和连续傅里叶变换；计算方便，可以通过并行处理来提高处理速度；理论发展清晰，大多数是由消混叠复原法发展而来。但是缺点也同样明显：所建立的运动模型都是平移模型，不具有一般性；在频域中，难以利用正则化约束，这样就导致难以使用图像的先验信息来帮助进行超分辨率复原。因此，人们对频域复原方法的研究越来越少。发展最快，应用最广的是下面将要介绍的空域复原方法。

3.2 空域超分辨率复原方法

空域超分辨率复原方法是指在像素空间内，直接进行图像配准以计算序列图像之间的变换关系，然后使用一系列的约束来描述模糊和噪声等降质过程，进行迭代复原的方法。与频域复原方法目前只局限于平移运动模型不同，空域复原方法可以很方便地建立复杂的运动模型，包括全局运动模型和局部运动模型。同时空域复原方法很好地描述噪声、降采样、由于非零孔径时间造成的模糊、光学系统降质和运动模糊等众多复杂的过程，还可以加入更完善的先验知识，如Markov随机场理论和集合理论约束等。因此，空域超分辨率复原模型更符合实际的图像退化过程，能够得到很好的复原效果，是目前应用最广泛的一类超分辨率复原方法。

常用的空域复原方法包括非均匀空间样本插值法、滤波器法、迭代反向投影法、代数滤波后向投影法、凸集投影POCS法、统计复原法和混合MAP/POCS法等。

空域超分辨率复原方法的一般步骤如图5所示。

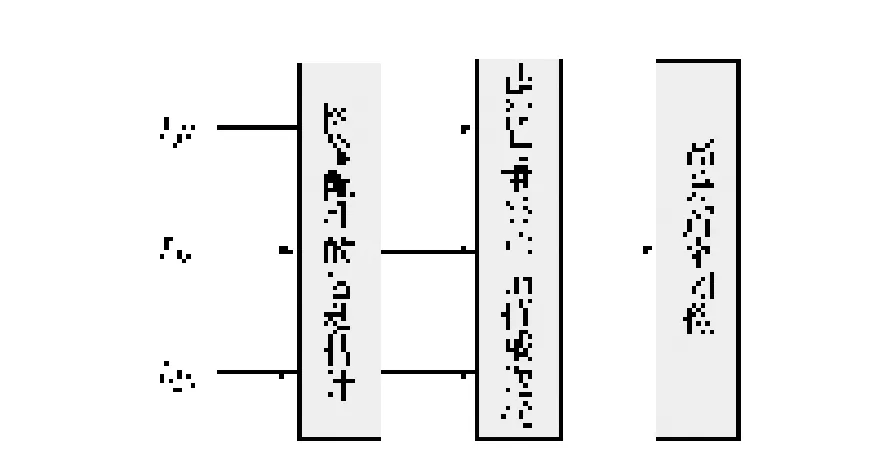
图5 空域超分辨率复原方法的一般步骤Fig.5 General steps of space domain super-resolution restoration

3.2.1 非均匀空间样本插值法

非均匀空间样本插值的思想比较简单，首先对图像序列进行配准，在非均匀采样间隔的网格点上产生采样值，这些采样值形成了一系列的复合图像，对这个图像进行降采样，最后解卷积进行模糊复原，就可以得到清晰的高分辨率图像。

文献［7］建立了整体平移和旋转的运动模型，进行迭代的内插和修正求解，解决了频域法中无法描述复杂运动模型的问题，但缺点是内插方式过于简单，对于频谱混叠不具有抑制作用。文献［8］提出一种新的内插方法，但是这种方法仍然无法满足需求，导致复原的高分辨率图像没有包含全部的高频信息，视觉效果无法令人满意。文献［9］引入了一种性能较好的图像复原技术，取得令人满意的复原效果。文献［10］将小波插值方法应用于超分辨率复原中，首先对低分辨率图像序列进行小波变换，在不同尺度的小波空间同时进行图像复原，最后合成得到高分辨率图像，取得很好的复原效果。

非均匀样本空间的插值方法原理直观，计算简便，速度较快的方法甚至能够做到实时处理。总的来说，非均匀插值方法的优势是它具有相对较低的计算负荷，并能进行实时应用。但是，该方法较为简单，没有涉及高频分离技术，复原之后的图像频率成分并没有超过成像系统的截止频率，同时当前的方法也没有考虑到图像序列模糊和噪声参数不一致的情况。

3.2.2 滤波器法

一些应用场合比如电视信号变换、超分辨率影视成像，不仅要求较好的复原精度，同时也要求复原的时间要短。滤波器法便是适用于这样场合的方法。

滤波器法认为视频序列是平稳因果图像序列［11］，假设低分辨率图像序列为y(t)，高分辨率图像序列为f(t)，序列之间存在相对运动，经过运动补偿后存在独立同分布的高斯噪声，则低分辨率图像序列y(t)为：

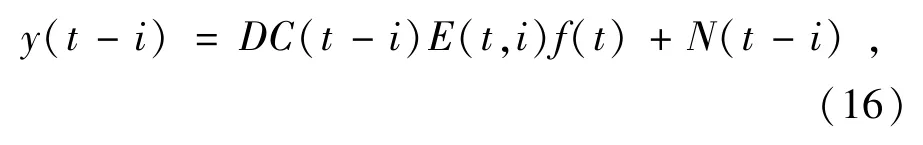
式(16)中：D表示降采样，C(t-i)表示第i帧低分辨率图像的降晰函数，E(t，i)表示帧间相对运动，N(t-i)表示模型中的噪声，噪声的自相关矩阵为W(t-i)-1。

定义误差函数为：

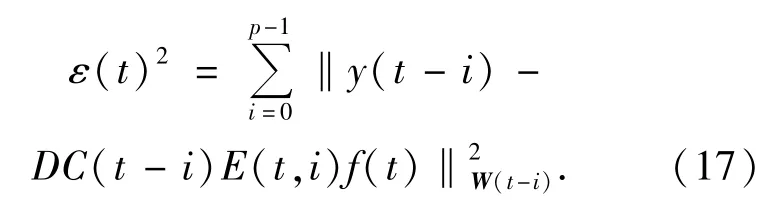
误差函数最小化的解就是复原得到的高分辨率图像。对式(17)进行求导，可得：

式(18)中：P(t)和R(t)分别如式(19)和式(20)所示。

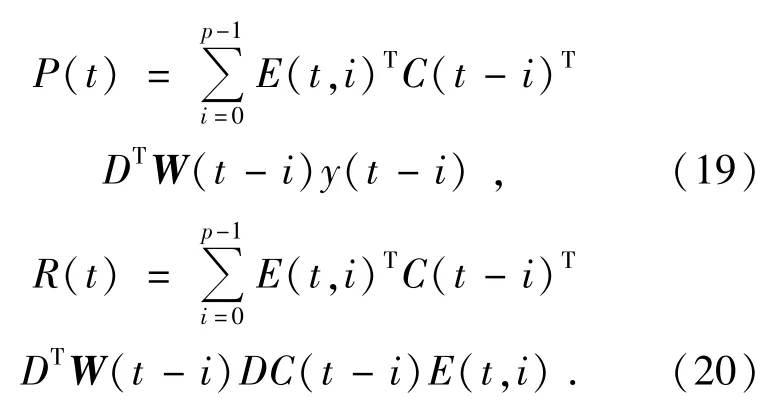
式(18)可以采用不同的方法求解，例如文献［11］中的梯度下降迭代算法，充分利用了前一帧的复原结果，具有很快的处理速度。Alam等［12］引入维纳滤波用以抑制噪声，对红外图像视频序列的复原结果证明了该方法的有效性和快速性。

总的来说，滤波器法应用到帧间信息较少，因此复原出的高分辨率图像质量并不能超过其他几种复原方法，但是该方法在计算效率上有很大优势，适用于一些特定的场合。

3.2.3 迭代反向投影法

迭代反向投影法是一个逆过程，该方法首先将估计的高分辨率图像投影到低分辨率的图像空间中，获得低分辨率图像的估计接着计算真实低分辨率图像和估计低分辨率图像的模拟误差，直到误差能量小于规定的阈值为止。迭代过程如式(21)所示。

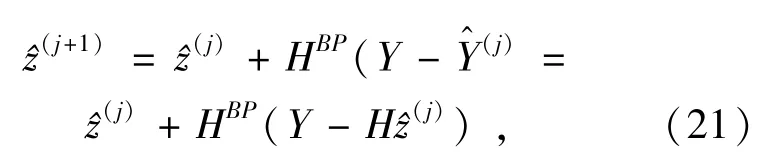
Irani在文献［13］中详细描述了迭代反向投影法。国内方面，郭伟伟、覃凤清、张永育等［14-16］对迭代反向投影法提出了一些改进，例如郭伟伟等引入傅里叶变换以估计帧位移，覃凤清等使用子像素配准方法，张永育等引入Keren改进配准算法，提高了配准精度。Maan［17］和Tom［18］等使用迭代反向投影法重建视频序列的高分辨率图像，取得了很好的复原效果。

迭代反向投影的复原方法首先需要确定反向投影操作数，当操作数选取不当时，算法有可能不收敛，即便收敛，不同操作数也会得到不同复原结果。同时，该方法的投影误差决定于先验约束条件，将先验约束引入是一个复杂的过程，大大增加了该方法的复杂度。

3.2.4 代数滤波后向投影法

代数滤波后向投影法是为了解决使用线性成像阵列对固定的场景多次一维扫描，然后进行三维复原这一课题而提出的，推广到二维图像的超分辨率复原中，只需要将传递函数由线积分改成面积分就可以。文献［11］中详细描述了这种方法。代数滤波后向投影法的优点是使用了层析图像领域中的复原技术，提高了超分辨率复原的效果，但是这种方法在建模中没有考虑观测噪声，在逆滤波过程中频率越高，响应越大，带来的问题就是这种方法对噪声非常敏感。尽管有明显缺陷，但这种由层析成像推广到二维超分辨率复原的方法仍然值得借鉴。

3.2.5 凸集投影POCS法

严格来说，凸集投影POCS法是集合理论复原的一类代表性方法，该方法的思想是使用一系列的凸约束集合来描述超分辨率复原方法中的一些特性和先验信息，例如图像正则化、数据可靠性和能量有界性等，这些凸约束集合会有一个相交的区域，这个区域就被定义为超分辨率复原图像的解空间。接着通过一定的约束条件在解空间中确定一个点，作为原始高分辨率图像的估计。凸集投影方法是一种迭代方法，通过不停的迭代计算可以定位解空间中所有的收敛解，直至满足条件。

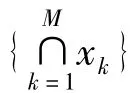
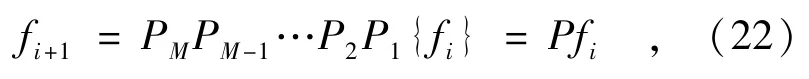
式中：Pj表示对应于第j个凸集的投影算子。显然，这是一个迭代方法，给定合适的初始迭代值，可以收敛到唯一解，从而最终获得满足要求的超分辨率复原图像，而如果没有限定初始迭代值，并且凸集满足紧致性，则解空间的任意一个值都是满足条件的复原结果。

凸集投影迭代方法的示意图如图6所示。

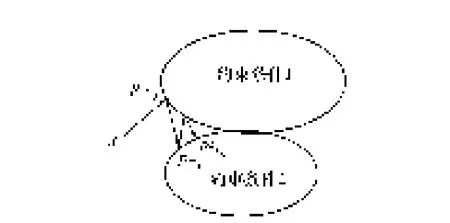
图6 凸集投影法示意图Fig.6 Diagrammatic sketch of POCS

POCS法拥有以下两个性质：

性质1：POCS法的解集也是凸集如下所示：

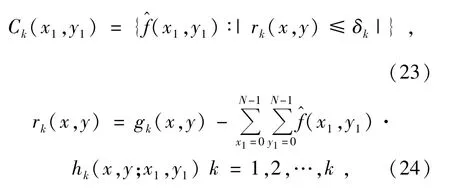
式(23)和式(24)中：f(x1，y1)为原始高分辨率图像为高分辨率图像的估计；hk(x， y；x1，y1)为观察图像在(x1，y1)处所对应的系统PSF；δk=cσ≥0为f(x1，y1)在Ck(x1，y1)内的统计置信度。

性质2：如果需要调整收敛速度，可以加入松弛迭代算子如下：

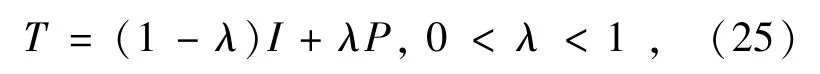
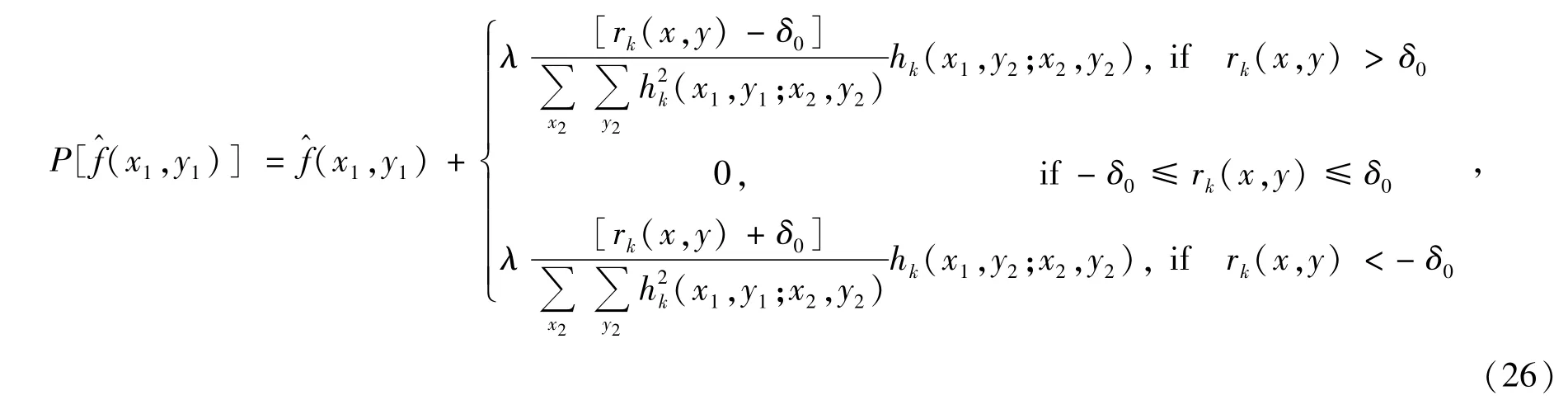
如果加入一些额外的约束条件，可以进一步加快收敛速度，例如加入幅度约束条件如下：

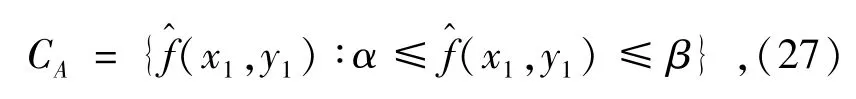
式中：α、β是可调整的常数，通常取α=0，β= 255。

最终得到的高分辨率复原图像估计如式下所示：

如果加入松弛迭代算子，则上式变为：

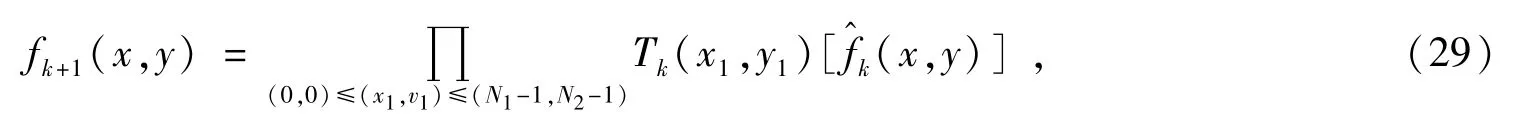
公式中：k=0，1，…，K，0≤x1≤N1-1，0≤y1≤N2-1。

一般而言，约束条件越多，迭代初始值选取得越准确，则这种方法的收敛速度越快。

Youla等［19］首次将POCS理论引入到图像复原中，而Stark等［20］首次将该理论用于超分辨率复原。但是，该方法复原结果中有可能出现振铃效应和吉布斯效应，文献［21-22］分别引入线过程模型和模拟-迭代过程，抑制了这两种效应，使复原图像更加清晰。Patti等［23］提出一种新的运动模型，该运动模型包含了空间变化的点扩散函数，考虑了光学系统降采样和相对运动模糊对图像质量产生的影响，随后又在文献［24-25］中优化了该方法，引入了频谱混叠和加性噪声等进行建模。

POCS方法的优点在于实现简单，并且便于使用先验知识，但是通常得不到唯一解，对边缘细节的保护能力较差，迭代次数一般较大，计算时间较长，同时收敛结果很大程度上取决于初始值的选取。统计复原法

3.2.6 统计复原法

在统计学中，以事先和事后估计为分类标准，常用的估算方法包括MAP和最大似然估算(Maximum Likelihood，ML)，MAP的定义是在已知先验知识的条件下，使事件出现的后验概率达到最大，而ML则是先验知识等概率出现的MAP的特例。在图像的超分辨率复原中，所谓的统计复原方法，也就是通过引入一系列的先验约束条件，把超分辨率复原问题转化为一个统计估算问题，可以是MAP，也可以是ML。

把原始高分辨率图像记为f(x，y)，把退化后的低分辨率图像记为g(x，y)，并且认为f(x，y)和g(x，y)均为随机场。根据Bayesian理论，在已知g(x，y)，f(x，y)出现的概率如下：

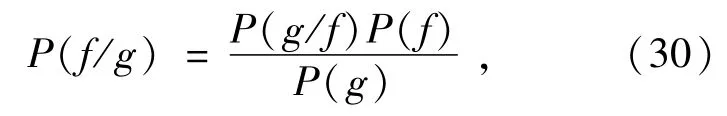
式中：P(f)和P(g)分别表示原始高分辨率图像和低分辨率图像的先验概率。P(f/g)为已知g(x，y)，出现f(x，y)的后验概率；P(f/g)为已知f(x，y)，出现g(x，y)的概率；适当地选择f，使P(f/g)达到最大，这时对应的f就是复原的最佳估计表示如下：

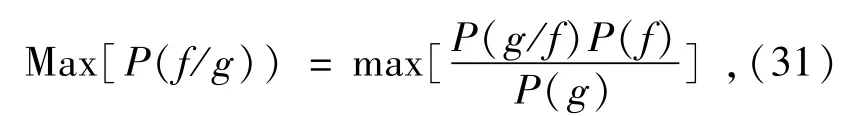
也即如式下：

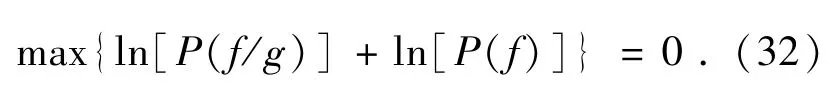
求解式(32)，可以使用上面提到的两种估算方法，即MAP和ML。

MAP方法，对式(32)进行求导，得到如下：

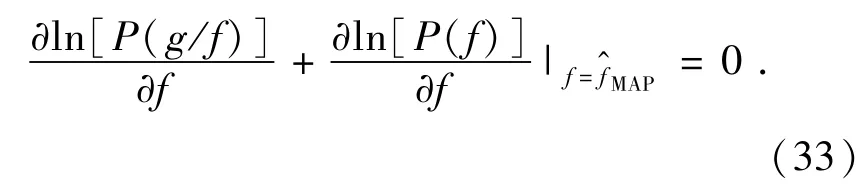
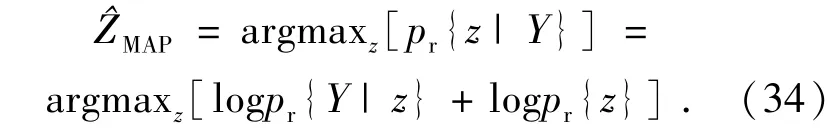
代价函数的前一项表示观察误差，第二项则由先验知识决定，这个代价函数的收敛性取决于先验知识，加入先验模型函数足够光滑并且是凸函数，那么代价函数就是收敛的，式(34)便可以求解。

ML方法则是先验知识等概率出现的MAP的特例，因此忽略公式(33)的第二项。ML方法表示如下：求解公式(35)可以得到满足条件的复原图像。

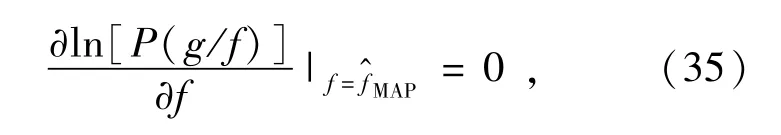
Schultz等［26］首次将MAP方法应用于图像内插中，随后又将其推广到超分辨率复原上，但是最初建立的模型比较粗糙，没有考虑运动模糊；在接下来的工作中，Schultz等为了得到较精确的运动估计参数，将亚像素级运动估计方法引入到他们的方法中，提出了基于块运动估计的投影模型和基于光流法的运动估计模型，较为精确的运动估计大大提高超分辨率复原的精度，但是这种运动估计是基于相邻两帧图像的，如果使用多帧的运动信息，可以得到更加精确的估计。Hardie等［27］提出可以对运动估计和超分辨率复原同时进行计算的方法，这种方法虽然计算速度较慢，但却克服了传统的运动参数需要从低分辨率图像中获得的缺点，取得较好的复原效果。国内方面，鲜海莹等［28］提出将低分辨率序列的位移信息作为一种非冗余信息，与MAP复原方法相结合；王静等［29］将MAP方法应用于遥感图像超分辨率复原，并提出一种频域校正方法，复原结果令人满意。

统计复原法目前已经被人们广泛接受，原因在于统计复原法可以很方便地引入各种先验知识，建立直观的模型，并且由于文献［27］的工作，可以将运动估计和超分辨率复原同时进行计算，大大提高了复原精度。

3.2.7 混合MAP/POCS法

MAP方法和POCS方法是当前学者们研究最多的，应用也是最广泛的方法，这两种方法都很容易在模型中加入先验知识，但是各自存在的优缺点也相当明显：POCS法迭代次数一般较大，计算时间较长，同时收敛结果很大程度上取决于初始值的选取，难以收敛，通常得不到唯一解，同时对噪声比较敏感；MAP法抗噪能力较强，收敛速度快且有唯一解，但是对边缘的保留能力较差。因此研究者们考虑将二者进行结合，以期待新的方法能同时拥有二者的优势。混合MAP/POCS法的思想是将MAP的代价泛函约束在某些集合中如下式：

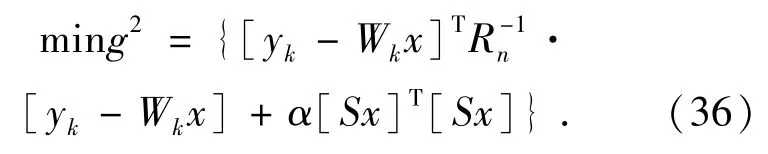
式中：x∈Ck，1≤k≤M，Rn是噪声的自相关系数，S是拉普拉斯算子，加权矩阵V用以控制平滑程度，Ck为外加约束条件。

目前这类方法研究的人不多，Elad等［30］把MAP和非椭球约束结合在一起，该方法可以使用全部的先验知识，并且能最终确定唯一的复原图像。通过实验表明，将二者相结合的方法确实能提高超分辨率复原的性能。

3.2.8 其他方法

除了以上介绍的几种常用的空间域方法之外，学者们还提出了很多其他的方法，主要包括：基于小波变换的方法、基于学习的方法和基于压缩域的方法。

基于小波变换的方法：小波变换采用不同的小波基近似逼近原始信号，在时域和频域均具有良好的局部化性质，尤其对高频成分可以进行精确的描述。通常在小波域，图像的高频分量和低频分量是分离的，图像的主要信息集中在低频分量，而细节信息集中在高频分量，而噪声通常是均匀分布在整个小波域的，因此小波变换可以方便描述图像的性质，目前已经广泛应用于去噪、去模糊和自动目标识别等图像处理的各个领域。由于小波变换良好的性质，学者们将其引入到超分辨率复原方法中。基于小波变换的超分辨率复原方法可以分为两大类：第一类是对低分辨率进行小波变换，在小波域对图像进行配准和插值，再进行小波逆变换得到高分辨率图像；第二类是使用低分辨率图像的小波变换系数来估计高分辨率图像的小波变换，最后进行逆变换。Tao等［31］提出将小波变换与双线性插值相结合，实现图像的边缘增强。Nguyen等［10］提出的方法就是对低分辨率进行小波变换，在小波域对图像进行配准和插值，开启了小波域超分辨率复原的先河。目前小波超分辨率复原方法尚处于起步阶段，具有广阔的发展前景。

基于学习的方法：随着人工神经网络在机器视觉和图像处理方面的广泛应用，学者们提出了基于学习的超分辨率复原方法。该方法使用人工神经网络，通过大量的训练样本学习，找到低分辨率图像序列和高分辨率图像的对应关系。人工神经网络方法实际上是训练鲁棒分类器的过程，并未过多地涉及超分辨率复原的概念。Hertzmann等［32］将神经网络引入超分辨率复原中，在不同的图像之间进行类推计算。Baker和Kanade［33］研究的是图像放大问题，使用神经网络进行分类训练。

基于压缩域的方法：因为当前的视频或者图像都是采用某种压缩方法进行存储的，在压缩编码中可能会引入噪声、块效应和振铃效应。因此研究基于压缩域的复原方法具有现实意义，例如Gunturk［34］将压缩过程中产生的量化噪声和图像自身的加性噪声结合起来，用两种方法进行建模处理。

4 总结比较

频域法的主要理论依据是傅里叶变换的平移特性，通过在频域内进行插值复原。频域法的优点是：原理简单清楚，计算方便，可以通过并行处理来提高处理速度；理论发展清晰，大多数是由消混叠复原方法发展而来。频域法的缺点是：所建立的运动模型都是平移模型，不具有一般性；在频域中，难以利用正则化约束，这就导致难以使用图像的先验信息来帮助进行超分辨率复原。目前，频域法已经不再是主流的超分辨率复原方法。

相比之下，空域复原方法可以很方便地建立复杂的运动模型，同时考虑了几乎所有的图像降质因素，例如噪声、降采样、由于非零孔径时间造成的模糊、光学系统降质和运动模糊等，还可以加入更完善的先验知识，如Markov随机场理论和集合理论约束等。因此，空域超分辨率复原模型更符合实际的图像退化过程，能够得到很好的复原效果，是目前应用最广泛的一类超分辨率复原方法。

在空域超分辨率复原方法中，使用最多的是POCS法和MAP法。POCS法迭代次数一般较大，计算时间较长，同时收敛结果很大程度上取决于初始值的选取，难以收敛，通常得不到唯一解，同时对噪声比较敏感。MAP法抗噪能力较强，收敛速度快且有唯一解，但是对边缘的保留能力较差。为了提高POCS法的快速性，可以加入松弛迭代因子，同时，也可以将POCS法和MAP法相结合，得到混合MAP/POCS方法。混合方法具有两种方法的优势，既能得到唯一解，又可以较好地保留图像的边缘细节。

POCS法和MAP法的复原结果比较如图7所示。

图7 凸集投影法与最大后验概率法的复原效果比较Fig.7 Recovery effect contrast of POCS and MAP

图7中，图7(a)低分辨率序列图像中的一帧图像分辨率为256×256；图7(b)POCS算法结果的图像分辨率为512×512；图7(c)MAP算法结果的图像分辨率为512×512。

5 结束语

超分辨率复原方法经过多年的发展，已经形成了完整的理论体系，同时获得了广泛的应用。在研究了众多的超分辨率复原方法的基础上，笔者认为未来超分辨率复原方法的发展方向主要有以下几个方面［35］：

(1)探索有效的抑制噪声的复原方法。在成像过程中，噪声是一个重要的退化因素。传统的超分辨率复原方法往往没有考虑噪声的影响，在图像包含噪声时复原性能迅速下降。因此研究抗噪性能较好的复原方法，以便从包含较多噪声的低分辨率图像中复原出清晰的高分辨率图像，是超分辨率复原方法发展的一个重要方向。

(2)研究有效的超分辨率方法评价体系。超分辨率复原结果是好是坏，不仅需要人眼的主观评价，更需要一个客观的评价标准。目前人们常用峰值信噪比(Peak Signal to Noise Ratio，PSNR)、结构相似性(Structural SIMilarity，SSIM)等通用的评价指标以衡量复原效果，并没有专门评价超分辨率复原效果的指标。如何才能有效地评价超分辨率复原方法的性能，既是超分辨率复原领域的一个亟待解决的问题。

(3)快速超分辨率复原方法。目前的超分辨率复原方法处理时间大多较长，并不能直接应用于光电经纬仪等对算法实时性要求较高的系统中。如何缩短算法的处理时间，提出快速超分辨率复原算法，是超分辨率复原实际应用中不可绕过的一个难题。

(4)探索精确有效的运动估计方法。运动估计是否准确，将大大影响超分辨率复原的精度。虽然目前出现了众多的运动估计模型，甚至有些方法已经达到亚像素的运动估计精度，但是目前的运动估计方法均局限于在低分辨率图像上进行估计，甚至于频域法只能建立整体平移的运动模型。总的来说，现有的运动估计方法无法令人满意，需要进行深入的理论研究和创新，提出新的运动估计模型。

(5)建立更加完善的图像退化模型。从原理上来说，任何一种超分辨率复原方法，首先都需要建立图像退化模型，然后对这种模型进行逆推，重新复原出高分辨率图像。所建立的模型是否准确，对复原精度有着直接的影响。目前多数的图像退化模型都只考虑了一部分因素，或者是模糊，或者是噪声，或者是整体运动等，这样的模型只是对现实场景的近似，如果采用这种降质模型，无论使用何种理论方法都无法取得更好的超分辨率复原性能。但是另一方面，模型建立的太过复杂，又会影响该方法执行的效率，甚至导致该方法不收敛。因此如何建立更加完善的图像退化模型，在估计准确度和方法效率之间取得平衡，也是一个亟待解决的问题。

(6)在超分辨率复原方法中，考虑视频压缩和编解码技术引入的噪声、块效应和振铃效应，使超分辨率复原方法能够很好地应用于电视信号复原和压缩图像复原等领域。

(7)盲复原问题。在实际应用中，光学系统的点扩散函数和噪声分布并不是已知的，因此如何在这些参数无法获得的情况下，对图像序列进行盲复原，也是一个亟待解决的问题。

根据超分辨率应用范围的增加，必定会出现已有理论无法解决的难题。如何在理论上进行创新，始终是超分辨率复原方法的一个发展方向。

［1］李衍达，常迥.信号重构理论及其应用［M］.北京：清华大学出版社，1991.

LI Y D，CHANG J.Signal Reconstruction Theory and Its Application［M］.Beijing：Tsinghua University Press，1991.(in Chinese)

［2］KIM S P，SU W Y.Recursive high-resolution reconstruction of blurred multi-frame images［J］.IEEE，1993，2(4)：534-539.

［3］KIM S P，BOSE N K，VALENZUELA H M.Recursive reconstruction of high resolution image from noisy under sampled multiframes［J］.IEEE，1990，38(6)：1013-1027.

［4］SU W，KIM S P.High-resolution restoration of dynamic image sequences［J］.International J.Imaging Systems and Technology，1994，5(4)：330-339.

［5］BOSE N K，KIM H C.Recursive implementation of total least squares algorithm for image reconstruction from noisy，under sampled multiframes［J］.IEEE，1993，1：269-272.

［6］DAVILA C E.Recursive total least squares algorithms for adaptive filtering［J］.IEEE，1991，3：1853-1856.

［7］KEREN D，PELEG S，BRADA R.Image sequence enhancement using sub-pixel displacements［J］.IEEE，1988，1：742-746.

［8］AIZAWA K，KOMATSU T，SAITO T.Acquisition of very high resolution images using stereo cameras［J］.IEEE，1991，1：318-328.

［9］TEKALP A M，OZKAN M K，et al..High-resolution image reconstruction from lower-resolution image sequences and space-varying image restoration［J］.IEEE，1992，3：169-172.

［10］NGUYEN N，MILANFAR P.A wavelet-based interpolation-restoration method for super-resolution［J］.Circuits Systems Signal Process，2000，19(4)：321-338.

［11］ELAD M，FEUER A.Super-resolution restoration of an image sequence：adaptive Filtering approach［J］.IEEE，1999，8 (3)：387-395.

［12］ALAM M S，BOGNAR J G，HARDIE R C，et al..Infrared image registration and high-resolution reconstruction using multiple translationally shifted aliased video frames［J］.IEEE，2000，49(5)：915-923.

［13］IRANI M，PELEG S.Improving resolution by image registration［J］.CVGIP：Graphical Models and Image Processing，1991，53：231-239

［14］郭伟伟，章品正.基于迭代反投影的超分辨率图像重建［J］.计算机科学与探索，2009，3(3)：321-329.

GUO W W，ZHANG P ZH.Super-resolution image reconstruction with iterative back projection algorithm［J］.J.Frontiers of Computer Science and Technology，2009，3(3)：321-329.(in Chinese)

［15］覃凤清，何小海，陈为龙，等.一种基于子像素配准视频超分辨率重建方法［J］.光电子·激光，2009，20(7)：972-976.

TAN F Q，HE X H，CHEN W L，et al..A video super-resolution reconstruction method based on sub-pixel registration［J］.J.Optoelectronics Laser，2009，20(7)：972-976.(in Chinese)

［16］张永育，李翠华，余礼钹，等.基于Keren改进配准算法的IBP超分率重建［J］.厦门大学学报（自然科学版），2012，51(4)：686-69.

ZHANG Y Y，LI C H，YU L B，et al..IBP super-resolution reconstruction based on improvement approach of Keren registration method［J］.J.Xiamen University，2012，51(4)：686-69.

［17］MAAN S，PICARD R W.Virtual bellows：Constructing high quality stills from video［A］.Proc.of International Conference on Image Processing，Austin，TX，1994，1：363-367.

［18］TOM B C，KATSAGGELOS A K.Resolution enhancement of video sequences using motion compensation［A］.Proc of IEEE Int.Conf Image Processing，Lausanne，Switzerland，1996，1：713-716.

［19］YOULA D C，WEBB H.Image restoration by the method of convex projections：part I，theory［J］.IEEE，1982，2：81-94.

［29］STARK H，OSKOUI P.High resolution image recovery from image-plane arrays，using convex projection［J］.JOSA A，1989，6：1715-1726.

［21］黄华，孔玲莉，齐春，等.基于凸集投影和线过程模型的超分辨率图像重建［J］.西安交通大学学报，2003，37(10)：1059-1062.

HUANG H，KONG L L，QI CH，et al..Super-resolution image reconstruction based on projections onto convex sets and line process modeling［J］.J.Xi′an Jiaotong University，2003，37(10)：1059-1062.(in Chinese)

［22］肖创柏，段娟，禹晶.序列图像的POCS超分辨率重建方法［J］.北京工业大学学报，2009，35(1)：108-113.

XIAO CH B，DUAN J，YU J.POCS super-resolution reconstruction from image sequences［J］.J.Beijing University of Technology，2009，35(1)：108-113.(in Chinese)

［23］PATTI J，SEZAN M，TEKALP A M.High-resolution image reconstruction from a low-resolution image sequence in the presence of time-varying motion blur［A］.Proc IEEE Int.Conf.Image Processing，Austin，TX，1994，1：343-347.

［24］PATTI J，SEZAN M，TEKALP A M.Super-resolution video reconstruction with arbitrary sampling lattices and nonzero aperture time［J］.IEEE，1997，6(8)：1064-1076.

［25］PATTI J，SEZAN M，TEKALP A M.Robust methods for high-quality stills from interlaced video in the presence of dominant motion［J］.IEEE，1997，7(2)：328-342.

［26］SCHULTZ R R，STEVENSON R L.A Bayesian approach to image expansion for improved definition［J］.IEEE，1994，3(3)：233-241.

［27］HARDIE R C，BARNARD K J，ARMSTRONG E E.Joint MAP registration and high-resolution image estimation using asequence of under-sampled images［J］.IEEE，1997，6(12)：1621-1633.

［28］鲜海莹，傅志中，万群，等.基于非冗余信息的超分辨率算法［J］.电波科学学报，2012，27(2)：216-221.

XIAN H Y，FU ZH ZH，WAN Q，et al..Super resolution algorithm based on non-redundant information［J］.Chinese J. Radio Science，2012，27(2)：216-221.(in Chinese)

［29］王静，章世平，孙权森，等.基于MAP估计的遥感图像频域校正超分辨率算法［J］.东南大学学报，2010，40(1)：84-88.

WANG J，ZHANG SH P，SUN Q S，et al..MAP based remote sensing image super-resolution with frequency domain correction［J］.J.Southeast University，2010，40(1)：84-88.(in Chinese)

［30］ELAD M，FEUER A.Restoration of a single super-resolution image from several blurrd，noisy and under sampled measured images［J］.IEEE，1997，6(12)：1646-1658.

［31］HONGJIU T，XINJIAN T，JIAN L，et al.Super resolution remote sensing image processing algorithm based on wavelet transform and interpolation［J］.SPIE，2003，4898：259-263.

［32］HERTZMANN A，ANALOGIES A.Computer Graphics［M］.New York：Siggraph，ACM Press，2001.

［33］BAKER S，KANADE T.Limits on super-resolution and how to break them［J］.IEEE，2000，1：372-379.

［34］GUNTURK B K，ALTUNBASAK Y，MERSEREAU R M.Multiframe resolution enhancement methods for compressed video［J］.Signal Processing Letters，2002，9：170-174.

［35］陈健.基于POCS的红外弱小目标超分辨率复原算法研究［D］.长春：中国科学院大学，2014.

CHEN J.Research on infrared dim-small target super-resolution restoration arithmetic based on POCS［D］.Changchun：University of Chinese Academy of Sciences，2014.(in Chinese)

Correlation theory of super-resolution restoration method

CHEN Jian1，2，3，*，GAO Huibin1，WANG Weiguo1，ZHANG Zhendong1，LU Ming1
(1.Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Sciences，Changchun 130033，China；2.University of Chinese Academy of Sciences，Beijing 100049，China；3.College of Communication Engineering，Jilin University，Changchun 130012，China)

Firstly，the basic concepts and theories of super-resolution restoration method are introduced.Secondly，some applications focused on common method of super-resolution restoration are summarized.Their theoretical basis，advantages and disadvantages，and scope of applications are exhaustively analyzed.Finally，the future development of super-resolution restoration method is prospected.Overall，the super-resolution restoration methods are divided into frequency domain method and space domain method.Frequency domain recovery method is simple in principle and easy in calculation.But its motion model is shift model and doesn′t have a general.Meanwhile it is difficult to use the priori information of the image to help super-resolution restoration. With space domain recovery method，a complex motion model can be easily established considering almost all of the imaging degradation factors，including noise，down sampling，fuzzy caused by non-zero aperture，degradation of optical system，and motion blur.As the same time，we could also add more perfect priori knowledge.Compared to the frequency domain method，space domain super-resolution restoration model is moreclose to actual degradation processes and is currently the most widely used super-resolution restoration method.

super-resolution restoration；frequency domain method；space domain method；projection onto convex sets(POCS)

TP751.1

10.3788/CO.20140706.0897

2095-1531(2014)06-0897-14