直面落差,重拾教学的常识
2014-04-29许丽
不可否认,教的目标与学的结果之间总存在一定的落差。落差形成的原因是多方面的,如学习内容的难易、学生智能结构的差异等等,但也不乏教师教学本身的问题。很多教与学的落差,正是“教”单方面作用的结果。因此,正确认识教与学的落差,勇敢剖析教师的教对形成落差的影响,回归教学该有的常识,将成为缩小落差、提升教学效益的关键之一。
一、平移经验造成落差,教学需要清醒认识“学习的起点是什么”
在苏教版五年级“求一个数是另一个数的几分之几”的课堂教学中,听课老师发现了一个问题:在具体的情境中,学生不会找“单位1”。这种落差感,也纠结着上课教师。她在说课中提到:在上今天的新课前,书本上已经明确指出“一个物体、一个计量单位或许多物体组成的一个整体,都可以称为单位“1”。按理说,学生对单位“1”已经有了认知,有了寻找的经验,为什么在这节课上会出现这样的情况呢?为此,我们和该教师一起回忆了当时具体的教学情境。一些学生已经会找单位“1”,大致有两种情况:一是被平均分的一个物体(例如一块蛋糕)、一个计量单位(例如1米),由许多物体组成的一个整体(例如6面红旗)都可以看作单位“1”。二是在已经出现分数的句子中,是谁的几分之几,就把“谁”看做单位“1”,例如在“五年级一班的三好学生占全班总数的2/9”,思考并填充时,就是把“全班人数”看作单位“1”。
再来看新授课中要找单位“1”的情境:题中出现了长短两条彩带,没有明确告知把谁平均分(以往每条彩带都可以被看作单位“1”),也没有出现具体的分数,看来,非此非彼,寻找单位“1”的情境已经发生了变化。原来,以前我们研究的都是用分数表示部分与整体的关系,只要把整体看作单位“1”即可,而从这节课开始,分数的认识已经从部分与整体的范畴,扩展到两个同类数量,具体研究用分数表示两个数量之间的倍数关系,把谁看做单位“1”,关键要看把谁当做比较的标准了。
由此,我们找到了形成这次教学落差的真正原因:上课前,学生确实有了会找单位“1”的现实起点,但它与解决“求一个数是另一个数的几分之几”所需要的逻辑起点完全不是同一个起点。当学习的现实起点与逻辑起点本身存在落差,而教师又没有认识到,继续平移找单位“1”的经验来开展新的学习的话,教与学必然形成落差。因此,避免教与学的落差,读懂教材是关键。一个对教材的结构体系烂熟于心、对教材编排意图和学情都能准确把握的教师,才能摸清学生的现实起点,掐准学习的逻辑起点,展开有效的教学。
二、盲目苛求造成落差,教学需要正视“课堂中现在有什么”
在教学苏教版五年级“最大公因数”时,笔者感受到了教者因为现实与期望之间有落差时的失落。
课堂的一个片断进程是:教师安排学生尝试找一找6和9的公倍数有哪些,并一一巡视,大约6分钟后,老师首先展示了甲同学的方法:先找出6的倍数,再找出9的倍数,最后找出6和9的公倍数。接着出示了乙同学的方法,发现与甲同学相似,很意外:“你刚才不是先求9的倍数,然后说再从里面找出6的倍数,最后找出6和9的公倍数吗?”乙同学一脸无辜:“不是的,我开始跟你说的意思,不是这样的。”教师很失望:“你刚才是这样说的,这是最好的方法呀!”师生僵持着,课堂一时颇为尴尬。
此时的执教者到底需要什么?是什么让他如此心生落差?回想刚才他在巡视时忙碌寻找的背影,细析他“你刚才这样说”时的急切,“这是最好的方法呀”的肯定,无疑,他在等待一个心中最满意的答案(从9的倍数中直接找出6的倍数,再找出6和9的公倍数,这是教材提供的最快捷的方法)。事实上,学生在本子上到底写了什么,笔者的了解是:大多数同学只能零碎写出一两个答案,其中有对的,有错的,思考无序,也有部分同学用方法1一一罗列,有序思考,少数同学不会做,采用方法2的同学基本没有。
有些落差只是教师个人的心绪体验,往往是期望值高于现实而形成的,根源还在教师的本我主义和从速心理。正如上述案例中,教师一直在寻找心中最好的方法,并且想轻松地通过一个展示传递给大家,可是学生给不了,于是心理落差显现出来。要避免这样的落差,关键还在教师。如果教师稍加转身,全面去关注一下,课堂中现在有哪些答案,然后理一理交流顺序:能找出1个答案的同学先来交流,能找出更多的继续补充,能有序找出全部的再来展示,引一引还有没有其它方法,选一选大家更喜欢哪种方法,或许,教学就会走进另一番天地,解题无法的懂法了,思考无序的有序了,只会找出零碎几个的,能整体找全了。学生有自己的认知节奏,课堂有自己的生态资源,放低重心,放慢节奏,在“有”上做文章,教学才会跨越落差,平稳衔接。
三、简单告诉造成落差,教学需要追问“为什么可以这样”
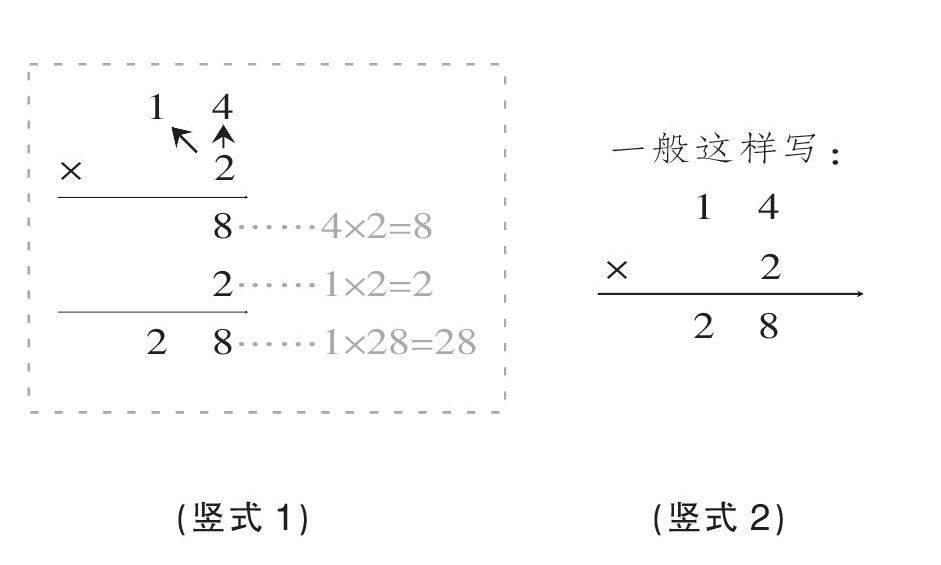
在教学苏教版二年级“乘法”的课尾,有学生询问老师:我不喜欢简便写法(见竖式2),我可以用原来的方法(竖式1)做题吗?
简单的,学生不喜欢;复杂的,学生感觉很好,老师愕然,又是一次教与学的落差!虽然这种落差不一定具有普遍性,但却有深究的意义。课后,笔者了解了这个同学的想法,他说:“我觉得竖式1的过程清清楚楚,一看就懂。用竖式2计算,有点迷糊。”是什么造成了这个同学奇怪的想法?此时,再次阅读教师在新授部分的教学就显得尤为必要:
师:要算14×2是多少,只要先算2个4得8,再算2×10得20,最后把8和20合起来就行了,大家懂了吗?
师:其实,14×2的竖式一般这样写。(出示竖式2)你会了吗?下面我们就用这样的方法来计算几道题。
原来,引进竖式2时,教师只是简单地告诉“一般这样写”,而为什么可以这样写,背后到底浓缩了哪些东西?它们又分别在竖式2的哪里得到了呈现?这些问题并没有在新旧竖式的比较中得到很好的沟通。学生是真实的求学者,他们对新知的悦纳,光凭教师简单的告诉是不会立即显效的,只有深究了简单背后的具体,理解了浓缩其中的精华,他们才会对新知产生认同,自觉建构,自信使用。教与学的落差,有时就是教的理所当然与学的莫名其妙之间的落差,要缩小这种落差,教学就不是简单地传递“是什么”,而需要适时多追问几个“这是为什么”,让隐性的东西显性化,知识才会在明了中被理解,在理解中被接纳。
当然,平移经验、盲目苛求、简单告诉,只是落差原因形成的一些方面,读懂教材、重视生成、理清重点,仅是减少和缩小落差行动的基本路径。如果我们重拾教学常识,用警醒的态度感知落差,用研究的方式有效地利用落差、自觉地改进落差,相信教与学双方都会进一步享受到数学的美景。
(许丽,宜兴市实验小学,214200)
责任编辑:宣丽华
