“见模”与“建模”，做实教学过程

蔡凤娟

小学数学的学习内容中，模型无处不在，数学的概念、性质、算式、图表等都是数学模型，师生几乎每一节数学课都在与它们打交道. 但如果学生只是接触到数学模型，不懂得模型的内涵，充其量只能算是“见模”，而不是“建模”. 怎样才能帮助学生有效建模？这需要我们根据学生的认知规律，不断地优化学生的认知路线，用数学建模的思想来指导数学教学. 一、把握建模时机

“建模”的过程，实际上就是“数学化”的过程，是学生在数学学习中，获得某种带有“模型”意义的数学结构的过程. 建模的时机是否恰当，要看“数学化”的程度如何. 建模的时机不当，会使建模过程变成了简单的知识和技能的传授过程. 下面以“认识倍”为例剖析建模时机：

案例一：出示情境——3朵蓝花，6朵红花. 演示：把3朵蓝花看成一份，圈一圈，6朵红花可以圈2个圈，说明6里面有2个3，红花就是蓝花的2倍. 列式表示6 ÷ 2 = 3.

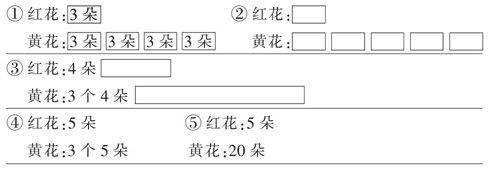
案例二：①演示后操作，每3朵一圈，6朵红花可以圈2个圈，红花就是蓝花的2倍. 用学具分一分，操作中感悟，（ ）里面有几个（ ），（ ）就是（ ）的几倍. 在脑子里想象操作过程. 三个活动，从“看”到“做”再到“想”，逐步归纳操作方法，建立“圈”的动作模型. ②数学表达. 先看图说，“把2朵花看成一份，红花里有3个2朵，所以红花是蓝花的3倍. ”再脱离具体物像说，“6里面有3個2，所以6是2的3倍”. 建立“××里有几个××，××就是××的几倍”的语言模型. ③抽象化. 逐步抽象，由实物图到集合图到数字信息，让学生说倍数关系. （如图1）④组织探寻算法.

比较两个案例，前一个案例中，老师让学生理解了6里面有几个2，就迫不及待地端出了算式，算式虽由学生说出，但学生并没产生建模的需求. 第二个案例中，老师先在学生的头脑中建立动作模型，再通过交流建立语言表达模型，然后去掉图例，摆脱对具象的依赖，激发学生用数学式表达两数倍数关系的需求，并最终根据除法的意义写出算式模型：（ ） ÷ （ ）. 两个案例都在帮学生建立“倍”的数学模型，但第二个案例时机把握得更恰当. 由具体、形象的实例开始，借助操作予以内化和强化，最后通过去形象化，归纳概括出数学表达式，赋予了“（ ） ÷ （ ）”更多的模型意义.

二、经历完整的建模过程

完整的建模过程分为这几个步骤：实际问题—建构数学基本模型—解决数学模型—运用检验模型（模型与实际问题间的互译与表达）. 经历完整的建模过程更有利于培养学生发现、分析、解决问题的能力.

以“求相差数的实际问题”为例：（1）提出问题：怎么让人一眼看出哪一种花片多？多多少？激发操作欲望. 学生提出用学具操作的办法. 追问：如果身边没带学具怎么办？有学生考虑画图. （2）建构模型：数量很大时画图方便吗？有没有更简便的方法？激发列式的需求. （3）解决模型：探索算法及算理. （4）练习巩固后拓展和深化：“小熊比小兔少跳多少下”还可以怎么说？（小兔比小熊多跳多少下？小熊再跳多少下就和小兔同样多？小熊跳的增加多少下就和小兔同样多？）除了用“……比……多（少）多少”来表示求相差数，你还知道哪些表示求相差数的说法？（……比……高（矮）多少？……比……长（短）多少？……比……贵（便宜）多少？）

“谁的花片更多，多多少”是一个实际问题，操作、画图使学生理解了这一生活问题的数学意义. 操作、画图的局限，让学生尝试寻找简洁的数学模型来解决问题. 解决求相差数的问题用加法还是减法，为什么用减法计算，这一数学活动是探究数学模型的解法. 在应用模型时，既有不同情境中的应用，还将相似的问题类化，通过解决一个典型，带动相关问题的解决，由一个到一类，渗透一种数学规律的思想，也就是模型思想.

三、关注模型的表达

数学模型在数学学习中无处不在，学生学习数学必然会利用一定的数学模型表达自己的数学思考. 研究学生数学模型的表达方式，既是为了正视学生的差异，也是为了检验建模的效果，更是为了通过数学建模改善学生的学习方式，改善老师的教学行为. 比如二年级下册学习了“三位数加三位数”的知识，学生建立了哪些数学模型呢？从问题库中就能看出学生对加法问题模型的不同理解.

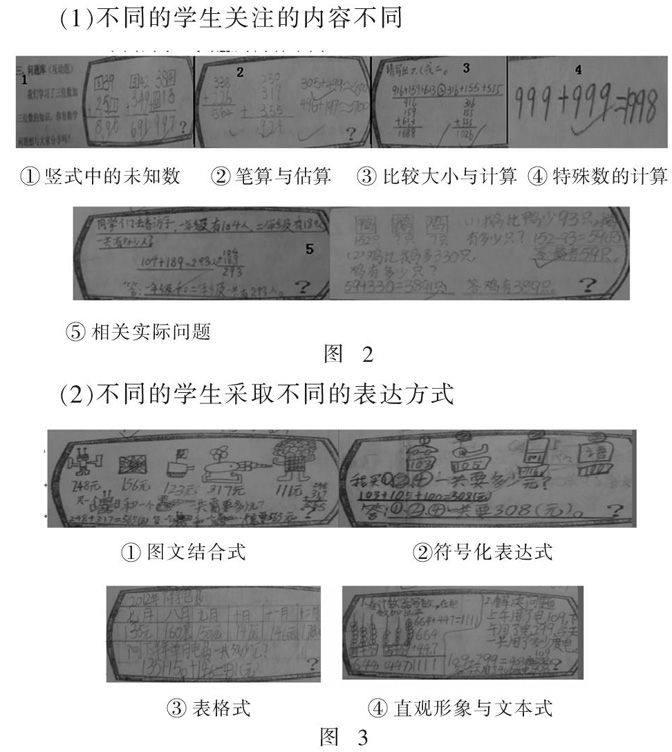
（1）不同的学生关注的内容不同

① 竖式中的未知数 ② 笔算与估算 ③ 比较大小与计算 ④ 特殊数的计算

⑤ 相关实际问题

（2）不同的学生采取不同的表达方式

① 图文结合式 ②符号化表达式

③ 表格式 ④ 直观形象与文本式

同样的三位数加三位数的加法问题，学生使用了多种形式表达自己获得的模型，有的只能称为模型的雏形，有的已经有了抽象化的意味，有的能多角度诠释加法模型的外延……这些模型给教师提供了丰富的信息，进一步解构就能成为我们制定教学计划的源泉.

建模思想的教学，融会在具体知识的教学过程中、教师的教学中，只有做好做实每一个师生的双边活动，学生才能由被动的“见模”变为主动的“建模”.