基于ELECTRE法的供应商选择研究

李坤 韩德春 李芝

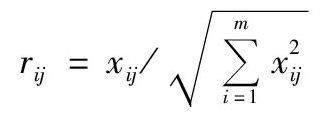
[摘要]针对核心企业与供应链伙伴关系中的关键问题——供应商选择问题，ELECTRE法即优劣系数法其基本思想是对任意两个备选方案，分别计算它们之间的优系数和劣系数，并通过引进一对控制参数，通过对优、劣系数的控制参数的比較和判断来确定方案的优劣。这样逐步淘汰劣方案，最后剩下一个或几个满意方案。而本文就采用了此种方法对供应商选择问题进行分析，方案获得了良好的排序效果，从而说明了该方法的实用性和有效性。

[关键词]供应商选择；ELECTRE法；供应链

[中图分类号]F252[文献标识码]A[文章编号]1005-6432（2014）6-0011-04

1引言

随着科技的进步，市场竞争越来越激烈，“横向一体化”的管理取代了企业与企业之间“纵向一体化”的管理。供应链管理的出现正是应对激烈的市场竞争环境以不断满足顾客需求，提高企业的核心竞争力。

在制造业中，采购成本在总成本中占据的比率较大，原材料的质量和交货期在很大程度上影响着制造型企业产品的生产与销售。因此，加强对供应商的选择和管理势在必行。

供应链合作关系的运行以供应商的评价选择为基础。互利互惠、信息分享、风险分担的供应商是核心企业所寻找的。而只有建立联系紧密的战略伙伴关系，才能达到低库存、低成本、高服务并适应市场要求的目标，实现核心企业与供应商的“双赢”模式。

在企业中，对供应商进行综合评价既是实施供应链管理的必经之路，也是供应链管理理论发展中的难点和重点。综合评价的关键是评价指标的确定，通过综述文献可以发现，根据Dickson整理出的评价供应商的23项准则[1]，供应商选择标准的关系要素一般从价格、质量、交货期和顾客服务这四个方面展开[2]；而哈默将TQCS（时间、质量、成本、服务）作为四大竞争要素；马士华在TQCS基础上增加了F（柔性）成为TQCSF。[3]本文在综合前人的成果下确定了四个评价指标即产品质量、产品价格、售后服务、交货情况。

供应商提供的商品可以满足企业需求的程度称为产品质量，作为评价供应商的最重要的指标之一，质量必须要有保障。这里可以用“产品合格率”来简单的表示产品质量，即产品的合格率越大，产品的质量越高。

企业购买单位产品所付出的成本称为产品价格，企业需要对成本进行分析，不可一味地追求低成本。有竞争力的产品价格是供应商选择的一个重要指标，双方都有利可赚才能创造互利共赢的局面。

综合评价供应商的另一个重要指标则是售后服务，往往双方的合作前景直接取决于服务水平的高低。供应商是否快速响应市场服务并建立售后服务体系正是企业考察供应商售后服务的重要依据。客户提出服务请求到及时解决的时间段为“客户服务请求解决时间”，在此用来表示售后服务，时间越短说明售后服务水平越高。

交货情况是指供应商及时满足企业订单或准时交货的情况，这就与供应商是否有充足的生产力、人力资源、较高的管理水平和技术水平有关。这里用“准时交货率”表示交货情况。

上述指标中，产品质量和交货情况属于效益型指标，即越大越好；产品价格与售后服务属于成本型指标，即越小越好。

供应商的评价选择的方法有：线性权重法、层次分析法、DEA方法、理想点法、ELECTRE法等，各方法不同，各有利弊。而ELECTRE法能够比较任意两个备选方案的各个指标的优劣，从而更加客观、公正、公平的选择出理想方案。

2基本概念和方法

ELECTRE法（Elimination Et Choice Translating Reality）即优劣系数法，最早是由Benayoun等（1969）提出的，其后，Roy（1971，1973，1977）、Nijkamp（1974）等人对之进行了完善。

ELECTRE法的关键是利用了 “超序”（outranking relationship）概念，也即当Ak在Al在数学意义上没有互相占优势，决策者也以某种风险程度认为Ak优于Al。这样通过一系列的超序关系评估，就可去掉那些超序关系意义上的劣方案。

ELECTRE法的分析步骤如下：

21计算规范化决策矩阵

利用公式：

rij=xij/m i=1x2ij（1）

进行规范化，可得规范化矩阵R=（rij）m×n

这里的xij是指第i供应商或方案第j指标的数值。

22计算加权规范化矩阵

若设V为加权规范化矩阵，则有：

V=RW=V11 V12 … V1j … V1n

… … … … … …

Vm1 Vm2 … Vmj … Vmn（2）

其中， Dkl={j|xkj

W=W1 0

W2

…

0 Wn

23确定属性优势集和劣势集

属性优势集Ckl的定义为：Ak方案的各目标属性优于Al方案相对应目标属性的属性标号集。

优势集可用下列式来表示：

Ckl={j|xkj≥xlj}（3）

劣势集为优势集的补集，意义正好和优势集相反，也即是所有劣的目标属性的标号集合。劣势集Dkl可表示为

Dkl={j|xkj

其中， J={j|j=1， 2， …， n}，即所有目标属性的标号集合。

24计算优势矩阵

由属性优势集可计算出所谓优势指数Ckl来。优势指数的定义为所有优势集中的标号对应的目标属性权重之和，也即

ckl=j∈CklWj（5）

优势指标反映了Ak相对于Al的重要性程度的大小，ckl越大意味着对所有的优势指标而言Ak对Al越具有优势，而0≤ckl≤1。当计算出所有方案对的优势指数ckl（k， l=1， 2， 3， …， n， k≠l）时，就构成了如下的所谓优势矩阵：

C=- c12 … c1m

c21 - c23 … c2m

… …

cm1 cm2 … cmm-1 -（6）

应当注意优势矩阵通常不是对称的，但有时是和对称的，即其中元素满足：

ckl+clk=1（k， l=1， 2， …， m， k≠l）

不过上式的成立要求不存在“相持”现象。

25计算劣势矩阵

我们利用下式来计算Ak劣于Al的程度：

dkl=maxj∈Dklvkj-vlj maxj∈Jvkj-vlj（7）

也即分子为属性劣势集中的标号所对应的两个方案的加权价值之差中的最大值，分母为所有目标属性的两个方案的加权价值之差中的最大值，两者相除则表示Ak比Al的劣势程度。

同样0≤dkl≤1。dkl值越小则意味着对所有的劣势指标而言，Ak越优于Al。

当计算了所有的劣势指标dkl（k≠l）后，可得如下的所谓劣势矩阵D：

D=- d12 … d1m

d21 - d23 … d2m

… … … …

dm1 dm2 … dmm-1 -（8）

一般来说，D矩阵也是非对称的。

让我们值得注意的是C矩阵和D矩阵中的信息并无所谓互补性，C矩阵中只包括权重的信息，而D矩阵则不但包括权重信息，而且包括方案的属性值信息。

26确定优势判定矩阵

如果我们给定一所谓优势指数阀值，则可认为当ckl大于或等于时，则真正有Ak优于Al的可能，也即ckl≥时，Ak方案有优于Al方案的可能。

阀值的给定可人为进行，也可用平均优势指标代之，即：

有：=1 m（m-1）m k=1k≠lm l=1l≠kckl（9）

根据阀值，我们可以构造一个0-1的矩阵F，其中元素为：

fkl=1若ckl≥

0若ckl<（10）

这个矩阵F的元素为1时，意味着具有优势机会（或可能），因而称F为优势判定矩阵。

27确定劣势判定矩阵

类似于F矩阵的建立，我们也可设置一劣势指标阀值，其确定方法也取平均劣势指标，即：

=1 m（m-1）m k=1k≠lm l=1l≠kdkl（11）

由则可得劣势判定矩阵G，其中的元素为：

gkl=1若dkl≤

0若dkl>（12）

gkl=1表示Ak不具有劣于Al的可能。

28确定综合优势判定矩阵

F与G中的对应元素相乘的结果，就构成了所谓综合优势判定矩阵E中的元素ekl。

29剔除较劣方案

根据综合优势判定矩阵E，即可开始方案剔除过程：对于Ak而言只有下式满足，它就不被剔除。

ekl=1l=1， 2， 3， …， mk≠l

eik=0i=1， 2， …， mi≠l（13）

式（13）的实际应用是较困难的，然而我们可以在E上直观地进行分析剔除方案，也即若任何列上只要有一个元素为1，则该列对应的方案剔除，因为这意味着该列方案为1元素对应的行方案所“压倒”。

3实证分析

作为自行车生产和消费大国，目前，我国自行车的拥有量约为6亿辆，年产量占到世界自行车总产量的1/3。 某自行车有限公司创建于1995年，是一家集设计、开发、生产、销售于一体的大型自行车及电动车企业，“XDS”商标被评为“中国驰名商标”，公司荣获“国家级高新技术企业”、“中国海关AA类管理企业”等荣誉称号。公司总占地面积450亩，年生产能力350万辆。下设业内规模最大的碳纤维公司，专业生产超轻型碳素纤维自行车车架、前叉、零配件及运动健身器材；有大型铝合金挤型车间；年生产能力超过200万台车架的轻合金车间；有国际一流的产品实验室。公司环境优美，被评为“园林式、花园式”工厂。公司主要生产山地车、公路车、旅行车、折叠车、童车、骑行装备，品种繁多，规格齐全。公司注重产品的质量，拥有雄厚的技术力量和完善的检测设施，并以严格的内部管理和产品质量控制系统、完善的售后服务，使产品获得良好的信誉。目前年生产能力逾300万辆，产品畅销全国各地，并出口国外，深受用户欢迎。

市场需求日趋个性化、多样化，制造业企业也正朝着专业化、协作化的方向发展。经过初筛，为铝合金自行车零件备选出4家铝合金制造厂。其铝合金自行车零件是利用本厂的铝材品种优势深加工开发生产的，产品独具特色，型材用料讲究，质量上乘，工艺严谨是多家自行车制造企业的A级供应商。

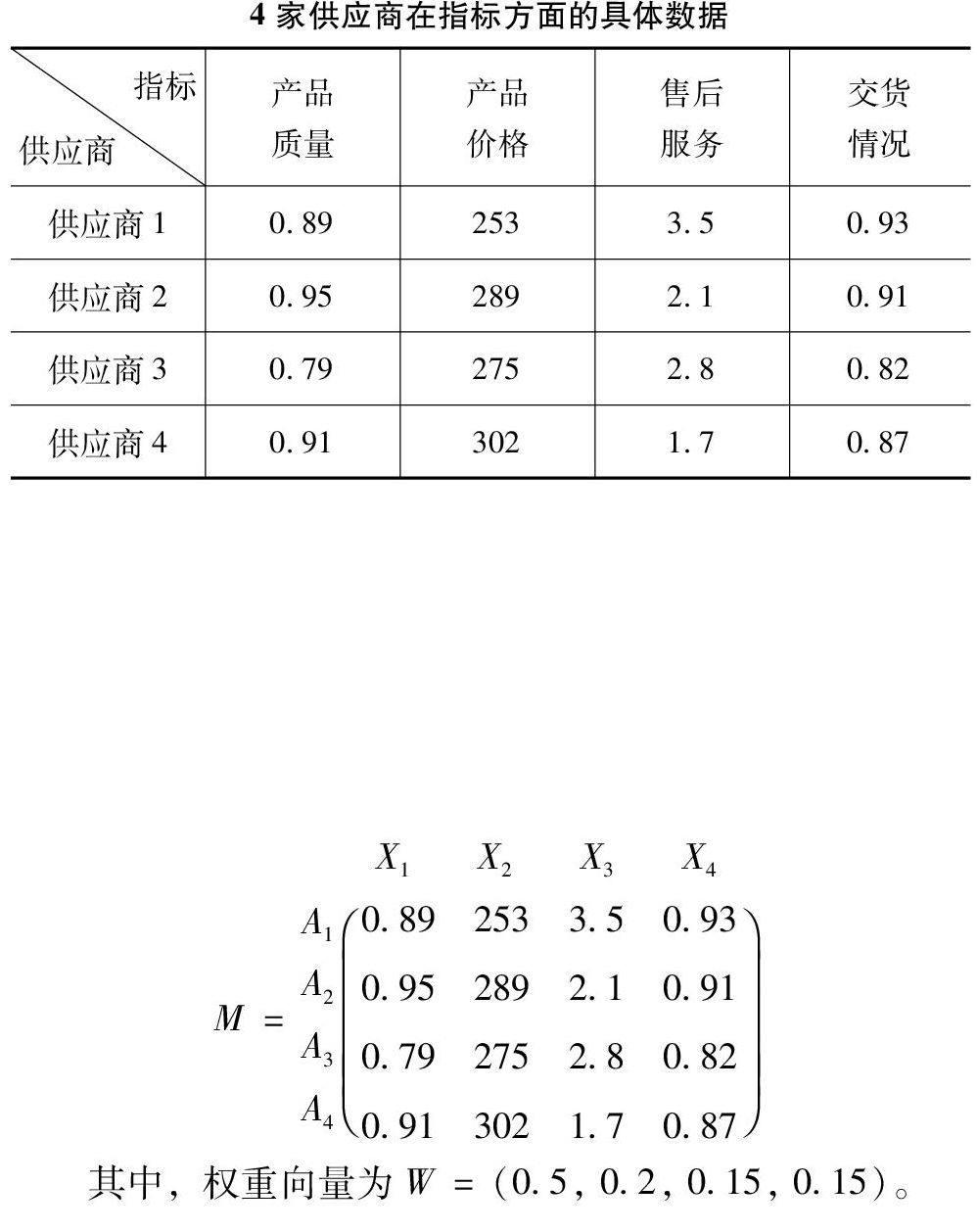
这4家铝合金制造厂在供应铝合金自行车零件的产品质量、产品价格、售后服务、交货情况[4]方面的具体数据如下表所示：

4家供应商在指标方面的具体数据指标

供应商 产品

质量 产品

价格 售后

服务 交货

情况供应商1 089 253 35 093供應商2 095 289 21 091供应商3 079 275 28 082供应商4 091 302 17 087

哪些供应商是首选的供应商？我们只有通过数学计算才可以得之。可以尝试使用ELECTRE法进行衡量，从中优选。

根据已知条件我们可以得到各供应商的各指标评价值的初始数据矩阵：

X1 X2 X3 X4

M=A1

A2

A3

A4089 253 35 093

095 289 21 091

079 275 28 082

091 302 17 087

其中，权重向量为W=（05， 02， 015， 015）。①计算规范化矩阵R

R=05017 04512 06688 05263

05355 05154 04013 05150

04453 04905 05350 04641

05130 05386 03248 04924

②计算加权规范化矩阵V

V=02509 00902 01003 00789

02678 01031 00602 00773

02227 00981 00803 00696

02565 01077 00487 00739

③确定属性优势集和劣势集，下面分别用1、2、3、4代表第一、第二、第三、第四个变量

C12={2， 4} C13={1， 2， 4} C14={2， 4}

C21={1， 3} C23={1， 3， 4} C24={1， 2， 4}

C31={3} C32={2} C34={2}

C41={1， 3} C42={3} C43={1， 3， 4}

D12={1， 3} D13={3} D14={1， 3}

D21={2， 4} D23={2} D24={3}

D31={1， 2， 4} D32={1， 3， 4} D34={1， 3， 4}

D41={2， 4} D42={1， 2， 4} D43={2}

④计算优势矩阵C

c12=j∈C12wj=w2+w4=035

c13=j∈C13wj=w1+w2+w4=085

c43=j∈C43wj=w1+w3+w4=080

优势矩阵为：

C=- 035 085 035

065 - 080 085

015 020 - 020

065 015 080 -

⑤计算劣势矩阵D

d12=maxj∈D12v1j-v2j maxj∈Jv1j-v2j

=max（00169， 00401） max（00169， 00129， 00401， 00016）

=00401 00401=10

d13=max（002） max（00282， 00079， 002， 00093）

=002 00282=07092

d43=max（00096） max（00338， 00096， 00316， 00043）

=00096 00338=02840

得如下劣势矩阵：

D=- 10 07092 10

03217 - 01109 10

10 10 - 10

03391 00096 02840 -

⑥确定优势判定矩阵F

先计算优势指数阀值

=（4 k=14 l=1ckl）/（4×3）=05

与C矩阵相比较

F=- 0 1 0

1 - 1 1

0 0 - 0

1 0 1 -

⑦确定劣势指数阀值

=（4 k=14 l=1dkl）/（4×3）=06479

与D比较后得

G=- 0 0 0

1 - 1 0

0 0 - 0

1 1 1 -

⑧确定综合优势判定矩阵E

将F与G中对应元素相乘得

E=- 0 0 0

1 - 1 0

0 0 - 0

0 0 0 -

⑨剔除方案

由E矩阵可知A1， A3可剔除，A2， A4选入。

我们可以优选出第二、第四个供应商。实践证明与这俩供应商是一种长期、稳定、双赢的关系。4结论

本文对供应链构建中供应商选择问题做了一些探究，重点用ELECTRE法解决问题，优劣系数法较好的应用于供应商的选择，实际应用中证明此种优选供应商的效果很好，方法可取。

参考文献：

[1]Dickson G WAn Analysis of Vendor Selection Systems and Decisions[J].Journal of Purchasing 1996，2（1）：5-17

[2]Elizabtch JWilsonThe Relative Importance of Supplier Selection Criteria A Review and Update [J].The International Journal of Purchasing and Materials Management，1994，55（6）：5-42

[3]馬士华，林勇供应链管理[M].北京：机械工业出版社，2000：106-113

[4]吴敏，徐玖平制造型企业战略联盟中供应商选择的“TOPSIS-AHP模拟”模型及实证分析[J].软科学，2006，20（4）：19-23

[5]左军多目标决策分析[M].浙江：浙江大学出版社，1991：78-88

[6]马士华，林勇供应链管理[M].北京：机械工业出版社，2006：16-19

[7]马丽娟基于供应链管理的供应商选择问题初探[J].工业工程与管理，2002（6） ：23-25

[作者简介]李坤（1988—），男，安徽舒城人，安徽工业大学管理科学与工程学院硕士。研究方向：物流管理；韩德春（1989—），女，山东潍坊人，安徽工业大学管理科学与工程学院硕士。研究方向：质量管理与质量工程；李芝（1990—），女，安徽舒城人，河海大学商学院硕士。研究方向：战略管理。