动物饲料配方的多目标优化模型
2014-04-29叶菊芳
叶菊芳

摘 要: 文章结合动物饲料配方的实际情况,建立了以成本最小、各营养素含量与需求之差绝对值最小为目标函数的多目标线性规划模型,并以0~6周雏鸡的饲养要求利用lingo软件求解模型,提出八种配方方案,供养殖户或饲料生产企业选择合理的配方方案。
关键词: 多目标线性规划 动物饲料配方 lingo软件求解
一、引言
畜牧业生产离不开饲料,饲料配方的好坏直接关系养殖户或饲料生产企业经济效益的高低。如何合理地选择各种畜禽的饲料配方,控制配方成本,提高饲料质量,是广大养殖户和饲料生产企业关注的问题。饲料配方的设计方案很多,但多是单目标优化设计方案,本文用多目标线性规划的方法解决饲料配方中的优化配合比问题。
二、问题描述及模型建立
三、模型求解
多目标优化问题的求解方法,往往化为单目标问题来求解[2]。这需要根据决策者对某个目标的重视程度采取相应的方法,对上述模型来讲,一种方法是选择其中一个目标作为目标函数,而其余作为约束条件求解,这样上述问题可化为m+1个模型进行求解,从而得到m+1个配合方案;另一种方法是给各目标函数一个权重系数,从而将多目标化为单目标函数。比较这m+1个优化方案再根据实际需要选择最合适的饲料配合方案。
若以成本最低为目标函数,各种营养含量达到最低要求为约束条件,则得如下模型:
下面以蛋用雏鸡为例说明模型求解结果。蛋用雏鸡饲养标准见表1[3],混合饲料的原料用玉米、麸皮、大豆柏、菜子柏、棉子柏、进口鱼粉、植物油、磷酸氢钙、石粉、食盐、赖氨酸、蛋氨酸,这些原料的各种营养成分及价格见表2[4]:
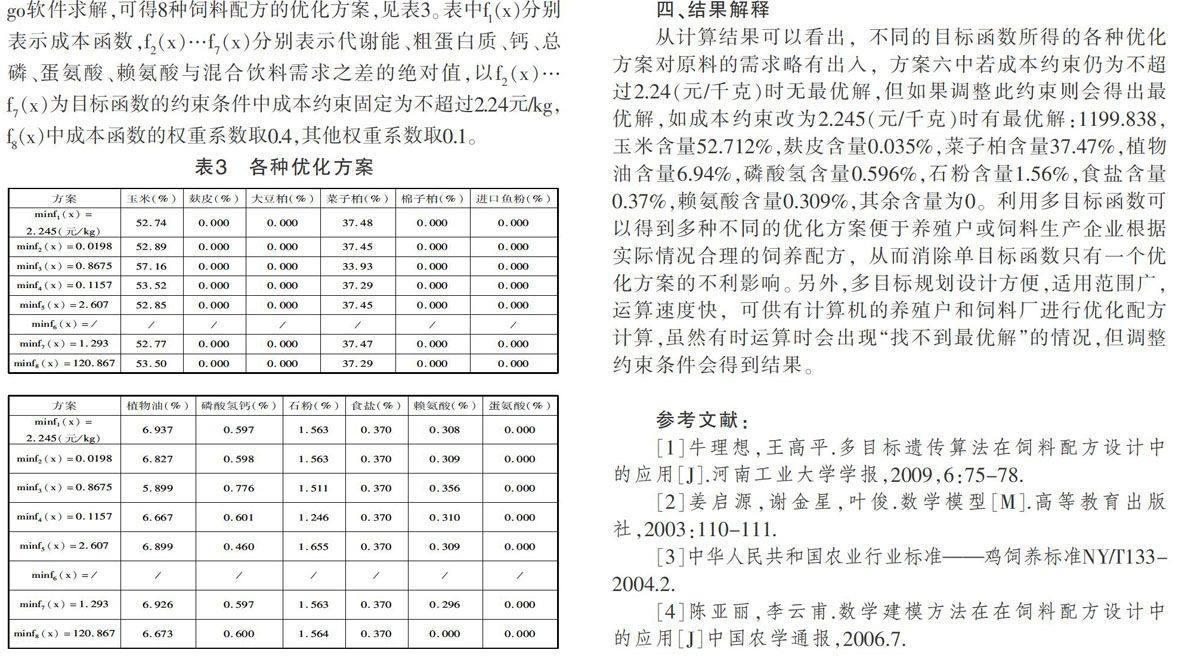
四、结果解释
从计算结果可以看出,不同的目标函数所得的各种优化方案对原料的需求略有出入,方案六中若成本约束仍为不超过2.24(元/千克)時无最优解,但如果调整此约束则会得出最优解,如成本约束改为2.245(元/千克)时有最优解:1199.838,玉米含量52.712%,麸皮含量0.035%,菜子柏含量37.47%,植物油含量6.94%,磷酸氢含量0.596%,石粉含量1.56%,食盐含量0.37%,赖氨酸含量0.309%,其余含量为0。利用多目标函数可以得到多种不同的优化方案便于养殖户或饲料生产企业根据实际情况合理的饲养配方,从而消除单目标函数只有一个优化方案的不利影响。另外,多目标规划设计方便,适用范围广,运算速度快,可供有计算机的养殖户和饲料厂进行优化配方计算,虽然有时运算时会出现“找不到最优解”的情况,但调整约束条件会得到结果。
参考文献:
[1]牛理想,王高平.多目标遗传算法在饲料配方设计中的应用[J].河南工业大学学报,2009,6:75-78.
[2]姜启源,谢金星,叶俊.数学模型[M].高等教育出版社,2003:110-111.
[3]中华人民共和国农业行业标准——鸡饲养标准NY/T133- 2004.2.
[4]陈亚丽,李云甫.数学建模方法在在饲料配方设计中的应用[J]中国农学通报,2006.7.
