基于门限极值理论的湖泊水质参照状态的确定
2014-04-28华祖林褚克坚河海大学浅水湖泊综合治理与资源开发教育部重点实验室江苏南京210098河海大学水资源高效利用与工程安全国家工程研究中心江苏南京210098河海大学环境学院江苏南京210098
华祖林,汪 靓,顾 莉,褚克坚(1.河海大学浅水湖泊综合治理与资源开发教育部重点实验室,江苏 南京 210098;2.河海大学水资源高效利用与工程安全国家工程研究中心,江苏 南京 210098;3.河海大学环境学院,江苏 南京 210098)
基于门限极值理论的湖泊水质参照状态的确定
华祖林1,2,3*,汪 靓1,2,3,顾 莉1,2,3,褚克坚1,2,3(1.河海大学浅水湖泊综合治理与资源开发教育部重点实验室,江苏 南京 210098;2.河海大学水资源高效利用与工程安全国家工程研究中心,江苏 南京 210098;3.河海大学环境学院,江苏 南京 210098)
在前人工作的基础上,利用门限极值的广义Pareto分布理论和超出阈值峰(Peak Over Threshold,POT)方法,提出了一种确定湖泊参照状态浓度的新方法.该方法不仅能够给出更为精确的置信区间,而且克服了广义极值分布理论取用数据浪费等缺陷.将该方法应用到太湖的水质基准参照状态中,通过POT方法对太湖8个站点1995~2006年总氮(TN),总磷(TP)和叶绿素a(Chl-a)的数据进行预处理,分别以-1.0mg/L, -0.05mg/L与-4µg/L作为它们观测值相反数的门限值,结果表明观测值的相反数符合广义Pareto分布,验证了方法的可行性.推荐采用25%分位点的值作为太湖总氮,总磷和叶绿素a的参照状态,即太湖的参照状态是:总氮0.66mg/L;总磷0.023mg/L;叶绿素a为1.27µg/L.最后分别得出了它们各自的95%置信区间,而且其精度明显高于广义极值分布理论结果.
湖泊水质基准;参照状态;门限极值理论;置信区间
为了准确衡量人类活动对生态系统的影响,必须确定生态系统的营养物基准,而参照状态浓度的确定是生态系统营养物基准制定过程中的核心环节之一.确定合理的参照状态对制定营养物基准乃至整个生态系统的保护都有重要的意义.目前,人们公认的参照状态浓度定义是由美国环境保护署[1]给出的,即“参照状态是环境自然的,受到人类活动影响最小或环境系统可达到的最佳状态”.
在当前情况中,特别是在经济发达,人口稠密的区域往往很难找到符合参照状态要求的湖泊,因此,国外研究者提出了参照湖泊法[2]、湖泊群体分布法[2]、古湖沼学反演法[2-3]、回归分析法[2,4-5]、模型推断法[2,6],三分法[7]等不同的建立参照状态的方法:同时我国学者也在实践中建立了国内不少湖泊的参照状态浓度,并在理论上对方法提出了不少改进.如:郑丙辉等[8]、陈奇等[9-10]根据太湖、巢湖和云贵高原湖泊的历史数据采用频率分析法建立了它们的参照状态:李小平等[11]利用古湖沼学反演法建立了淀山湖的营养物基准:董旭辉等[12-14]利用类似的技术重建了太白湖等湖泊的营养物的历史状态;顾莉等[15]利用改进的形态土壤指数法推断了太湖的总磷的参照状态;张礼兵等[16]基于系统动力学推断了巢湖的湖泊营养物参照状态;华祖林等[17]提出的广义极值法等.霍守亮等[18]总结了国内外学者在湖泊参照状态上的工作;许秋瑾等[19]比较了东部湖泊和云贵湖区在营养物控制标准上的区别.表1归纳了常见的建立参照状态方法及其优缺点比较.

表1 常见建立参照状态方法Table 1 Popular methods for estimating the reference conditions of lakes
虽然确定湖泊参照状态浓度的方法不少,但是,在实践中,出于对成本和方法简便易用性等问题的考虑,最常使用方法,如:参照湖泊法、湖泊群体分布法、三分法、频率分析法等都是统计学方法.而从表 1可以看出这些统计学方法都有一些缺陷需要克服:湖泊群体分布法和参照湖泊法需要的数据量巨大且不太适用于污染比较严重的湖泊;三分法的分类标准较死板;频率分析法虽然简单,但是对受人类活动影响巨大的湖泊是可能高估湖泊参照状态浓度的.更重要的是,以上这些统计学方法都未给出置信区间,因此难以评估其结果精度.
华祖林等[17]根据最小化人类对湖泊的影响以推断湖泊参照状态浓度的思想,利用广义极值分布理论推断了太湖总氮、总磷以及叶绿素 a的参照状态浓度,并有效地给出了它们的置信区间.虽然广义极值分布理论能够给出湖泊参照状态浓度的置信区间,但是由于这一方法在每年的观测值中只取最小的一个观测值,其余观测数据均被舍弃,肯定造成观测数据和信息的极大浪费.
针对多数统计学方法及广义极值分布理论不同的缺陷,本文基于门限极值的广义Pareto分布,采用超出阈值峰(POT)模型提出一种新的确定湖泊基准参照状态的方法.该方法能很好的克服广义极值分布理论的数据浪费和其他统计方法没有给出置信区间的缺点,并运用该方法确定了太湖总氮、总磷和叶绿素a的参照状态及其置信区间.
1 理论模型
从湖泊水质参照状态的定义可以知道,对于太湖这样受人类活动影响巨大的湖泊,其代表参照状态的良好水质状态是不太可能经常性的出现的.因此,为了最小化人类活动对湖泊水质的影响可以集中分析观测值中优于一定水平的水质状态以确定湖泊水质参照状态.但是,需要注意的是一般常用的统计学方法并不适用于这种观测值,而应该使用极值模型进行分析[20],门限极值理论就是极值模型的一种,并已经在相关学科领域表现良好[20-21].门限极值理论适用于对数据中较大值进行分析,而总氮、总磷和叶绿素 a等物质的浓度都是越小代表湖泊的状态越好,因此需要取总氮、总磷和叶绿素a原始观测值的相反数,以符合门限极值理论的要求,然后再进行分析.因此,本研究中总氮、总磷和叶绿素 a的负数是它们观测值的相反数,这一步骤只是为了计算的需要而做的数学上的处理,是计算过程的需要[19-20],而相反数的值本身无特殊的意义.
具体主要思想是:若湖泊中特定物质如总氮,总磷和叶绿素 a等物质的月观测值的相反数是平稳,无长时间相关性的;且其最大值构成的序列满足广义极值分布模型,则当 u→uend时有广义Pareto分布成立:
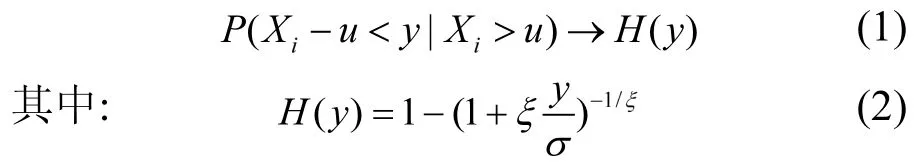
式中:Xi是观测值相反数;uend是观测值相反数Xi的右端点;y为一大于零的确定值;σ被称为尺度参数;ξ被称为形状参数.u即是门限值,也就是说只有超过该值的观测结果才参与模型的计算;特别值得指出的是门限值并不需要自己主观指定,可以用很多方法确定,而在这里利用平均剩余寿命图方法来确定.平均剩余寿命这个概念首先是来源于人寿保险和金融[20]等领域,即若定义 Xi的平均剩余寿命e(u)为:
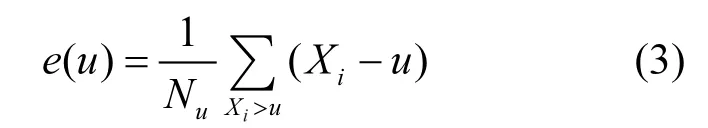
式中:Nu是超出门限值u的观测值相反数Xi的个数;u与 e(u)的关系图就是平均剩余寿命图.理论上可以证明若Xi满足式(1)和式(2),则e(u)在其门限值附近是与u近似成线性[20-21];因此,可以用平均剩余寿命图确定门限值u.
对于湖泊中的总氮、总磷等营养物的观测值而言,该模型成立条件中的平稳性和无长时间相关性是比较容易满足的,且可以用统计学方法检验其是否满足;而其相反数的最大值满足广义极值分布理论这一点也已经在文献[17]中得到论证.进一步,在实际应用中对于充分大的u0有:
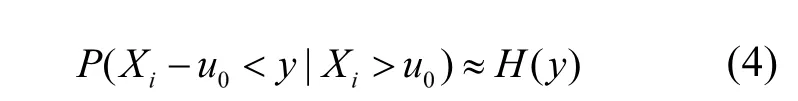
式(4)的2个参数有很多方法可以估计,最常用的就是极大似然法.主要思路是:假设 y1, y2,……,yk是k个超过阈值u0的观测值,则H(y)的对数似然函数为:
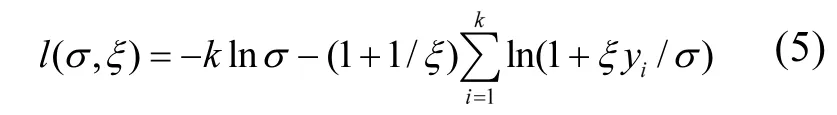
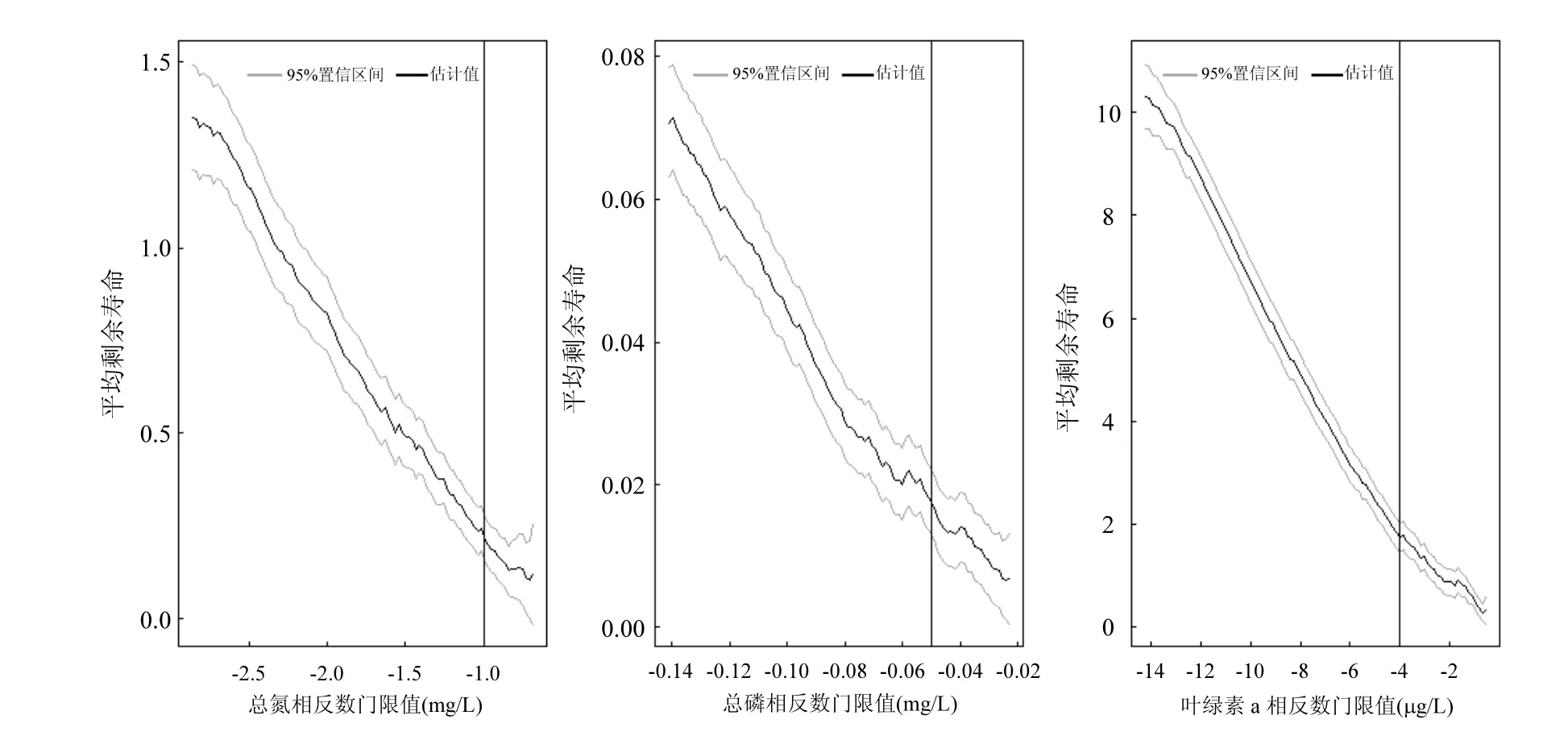
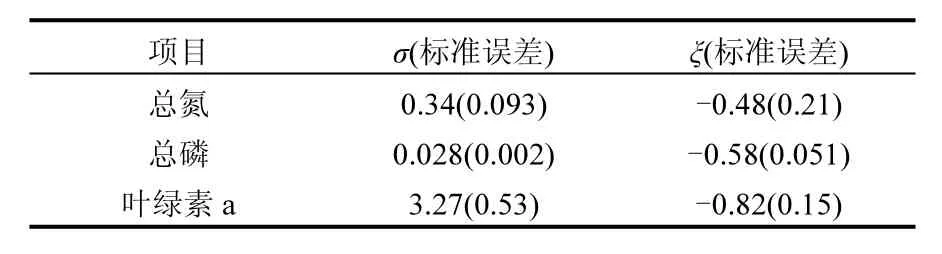
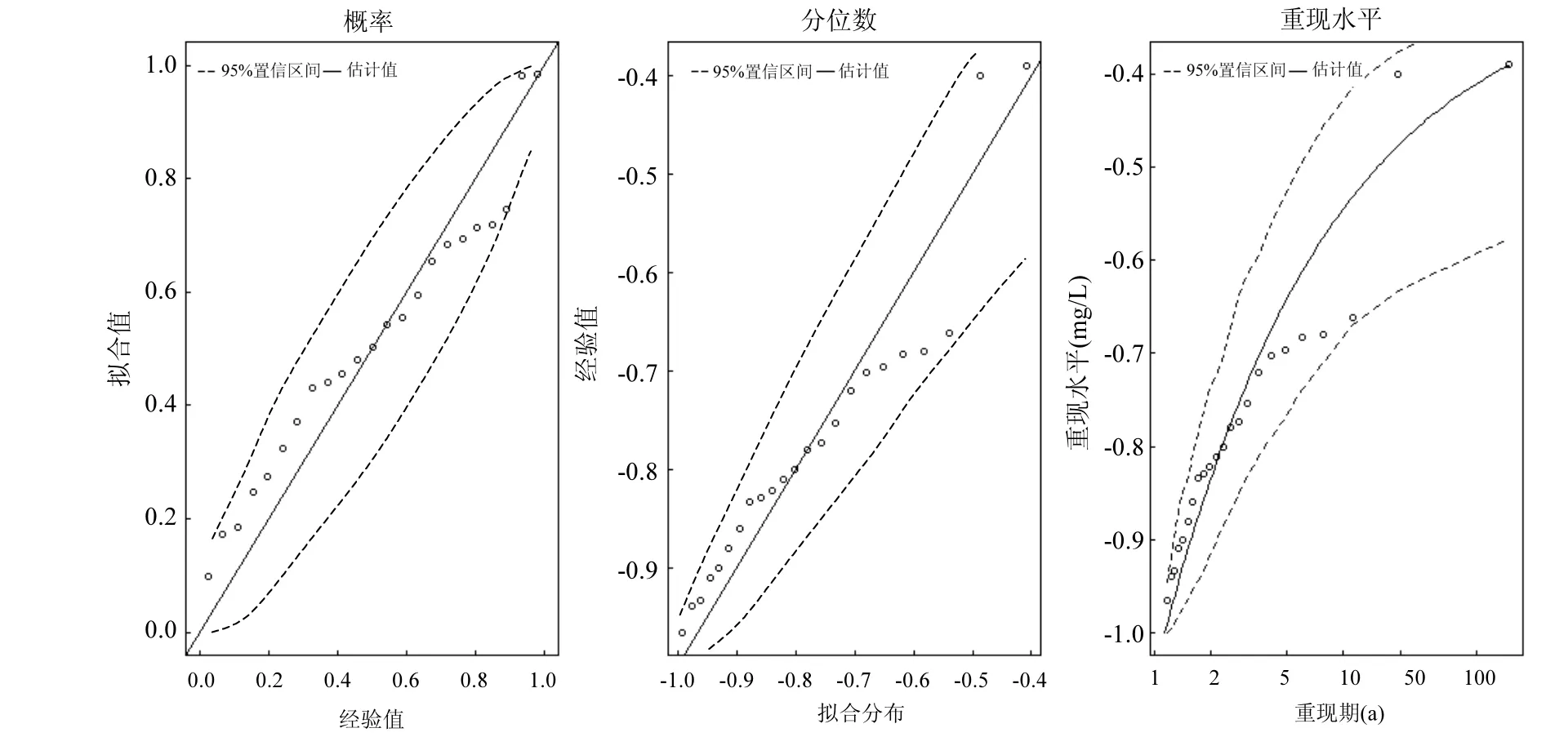
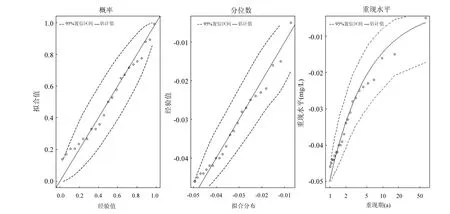
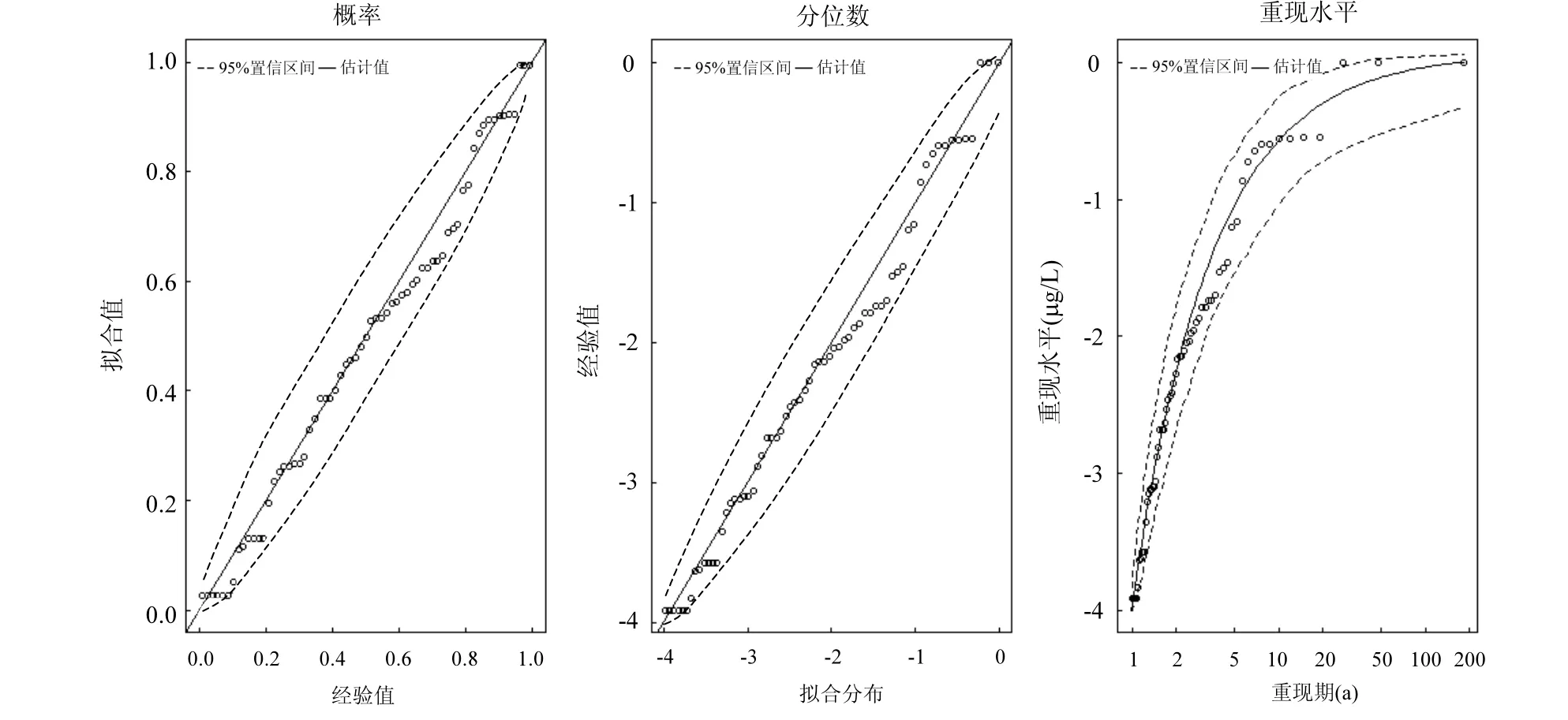
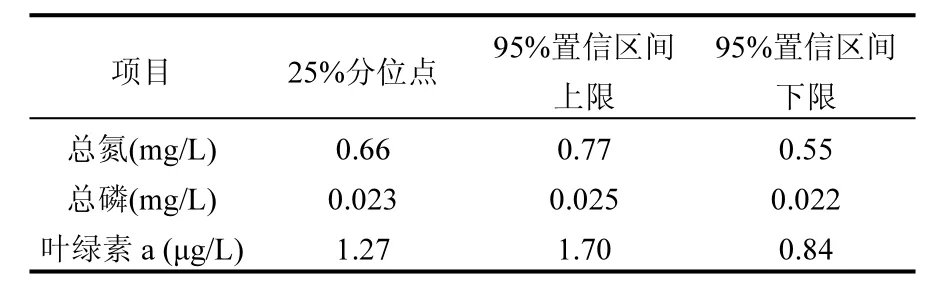
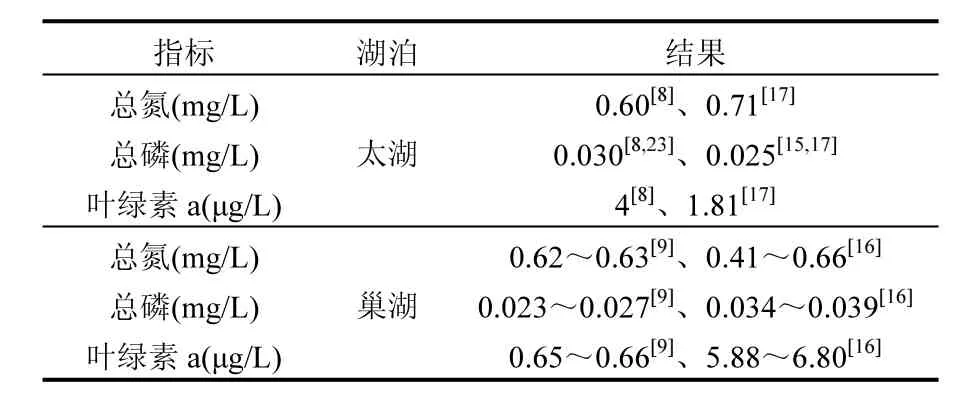
分别对σ,ξ求偏导,并令其等于零,则可以得到有关两个参数的方程组进而求出 2个参数的值.在一般情况下这一方程组并无解析解,所以需要使用如 Guass迭代法等数值方法求解.得到出两个参数值以后,对于0 式中:n为总观测值的个数,Nu0为超过门限值 u0的观测值相反数的个数.进而可以通过对数轮廓似然函数等方法估计置信区间,本文使用 Fisher方法估计置信区间. 2.1 数据来源 将门限极值模型应用于太湖参照状态浓度的建立中,数据来源于“中国生态系统定位观测与研究数据集—湖泊湿地海湾生态系统卷,江苏太湖站(1991-2006)”[22].在本研究中将观测的所有8个站点1995~2006年的数据都用于模型的建立,其中有极少数数据缺失,但是由于本模型并不基于时间序列的特性,因此少量数据的缺失并不影响模型的应用.根据前人研究结果,本文选用总氮,总磷,叶绿素a的观测值进行分析,建立太湖的参照状态浓度,每种物质有1145个数据. 2.2 数据预处理与POT方法 门限极值模型需要对每一个观测数据取相反数,但是其广义Pareto分布除了要求时间序列平稳且无长时相关性外,还要求超过门限值的观测值不能连续出现,这一要求的本质是保证用于建立模型的观测数据保持一定的独立性.在现实中,超过给定门限值的观测值往往会连续出现,如果时间序列中连续多个观测值大于门限值,则这些观测值就都会进入模型,从而使进入模型的观测值之间具有较强的相关性,这样就可能使该模型不再成立. 学者们提出很多不同的方法克服这一困难,比较常用的有马尔科夫链方法,POT方法等[19].其中 POT方法思路清晰,计算结果优异[22],因此本文首先使用POT方法,根据一定的准则粗略的把连续观测值分割成多个串,找出每个串的最大观测值,然后再选择适当的门限值,对这些最大值进行分析,构建门限模型,并进行统计检验. 目前为止,分割观测值没有规定的理论方法;本研究以保证分割后的序列能满足统计理论要求和尽可能保留更多的观测值为原则,经过反复试验,确定以-2mg/L、-0.1mg/L和-15µg/L为标准分割太湖总氮、总磷和叶绿素a观测值的相反数构成的序列依据:若连续4个月的观测值低于这些给定的值,则这些连续的观测值构成串,再将每一串观测值中最大的数据取出参与极值门限模型的建立.值得指出的是,这里给定的这些分割标准远远的超出相关文献中太湖参照状态的范围,因此这样分割并不会影响最后的统计分析结果,又能保留更多的观测值. 这样处理以后得到太湖总氮、总磷和叶绿素a的观测值中串的个数分别为77、97和127,显然,这也是总氮、总磷和叶绿素 a的观测值中真正参与建模的观测值的个数. 3.1 门限值的选择 对于门限模型来说,选择一个恰当的门限值是非常重要的:若门限值太小,那么所选择的数据可能严重偏离门限值模型:若门限值太大,那么超过门限值的观测值数目就非常少,将影响所建立模型的可信度.学者们通过统计学上平均剩余寿命图选取适当的门限值.当然,还需要参考所选取数值的环境学意义,综合考虑才能得到好的门限值.图1是总氮,总磷和叶绿素a的相反数通过预处理所形成序列的平均寿命.从图1可见,在总氮和总磷的相反数的剩余寿命分别在-1.0mg/L与-0.05mg/L附近,是近似线性的,也就是说该门限值是满足统计学要求的,且现行的湖泊总氮,总磷的三类地表水标准也是1.0mg/L与0.05mg/L,所以无论从统计学意义还是从环境学角度总氮和总磷相反数的门限值选为-1.0mg/L与-0.05mg/L是比较恰当的. 图1 门限值选择Fig.1 The Selection of a Threshold 对于叶绿素 a而言,根据太湖流域水资源保护局[24]推荐的湖泊富营养化评分与分类标准,结合图1中叶绿素a的平均剩余寿命图,确定选用-4µg/L作为叶绿素a相反数的门限值. 3.2 参照浓度的确定 表2 参数估计结果Table 2 The results of parameters estimation 表2是选择门限值以后对总氮、总磷和叶绿素 a观测值的相反数使用极大似然法估计参数的结果. 从表2可以发现,广义Pareto分布的形状参数及其 95%的置信区间都是负的,表明该模型有一个最大值,由于取了相反数,所以这意味着总氮,总磷和叶绿素 a的观测值存在最小值.由于天然湖泊总氮、总磷与叶绿素a的浓度应该有最小值,所以这与实际情况是一致的.同时,这一结果也与广义极值理论的结果一致[17].图2~图4分别显示了总氮、总磷和叶绿素 a的模型参数检验及其95%置信区间的结果. 图2 总氮相反数的模型检验Fig.2 Diagnostic plots of model fit to negative TN 从图2~图4可以看出,总氮,总磷的相反数都落在模型 95%置信区间以内,所以可以认为它们都符合门限极值模型;叶绿素 a虽然有一个值略微超出了重现期 95%的置信区间,但是超出的非常少,其它观测值的概率图、分位数图以及重现水平图都支持门限极值模型,再加上该观测值出现在重现期很高的区域,不太可能使用该值附近的分位数作为参照状态的依据,因此,可以认为叶绿素a也满足门限极值模型是没有问题的. 在选择恰当的分位点作为湖泊参照状态这个问题上,EPA[2]在参照湖泊法中推荐使用 25%的分位点的值作为湖泊的参照状态;在国内,由于长江中下游的湖泊受到人类社会和经济发展的影响较大,郑丙辉等[8],陈奇等[9]学者在用频率分析法,湖泊群体分布法等方法分析推断太湖、巢湖的参照状态时,采用所有观测数据的 5%的分位点作为太湖和巢湖的参照状态:华祖林等在用广义极值理论推断太湖参照状态时,由于极小值已经代表现代太湖最好的状态,他们也用 25%分位点的值作为参照状态.在本研究中,考虑到门限模型理论选择门限值过程已经去除了大部分水质不太好的情况,参与建立模型的观测值本身就代表了水质良好的情况,使用 5%分位点的值作为参照状态可能严重低估参照浓度,因此综合考虑使用 25%分位点作为太湖参照状态总氮、总磷和叶绿素a的浓度.表3是25%分位点的相关估计结果. 图3 总磷相反数的模型检验Fig.3 Diagnostic plots of model fit to negative TP 图4 叶绿素a相反数的模型检验Fig.4 Diagnostic plots of model fit to negative Chl-a 为了验证结果的可靠性,将国内学者之前对太湖的参照状态的研究与上述结果进行验证与对比分析.同时,考虑太湖参照状态研究结果不多,为了更好的验证结果补充了与太湖情况相近的巢湖的相关研究结论,具体结果可见表4. 从表 4可以看到,郑丙辉[8]等用频率分析法给出了太湖总氮和总磷的参照状态浓度分别为0.60mg/L及0.03mg/L,这一结果的总氮、总磷结果与本次研究得到的 25%分位点的值很接近.华祖林等[17]用广义极值理论给出的太湖总氮与总磷的参照状态浓度和 95%置信区间分别为0.71mg/L(置 信 区 间 为 :0.58~0.84mg/L)和0.025mg/L(置信区间为:0.018~0.033mg/L),显然其结果是非常支持 25%分位点作为太湖参照状态浓度的.顾莉等[15]用改进的MEI法给出太湖总磷的参照状态浓度为 0.025mg/L,这一结果也本研究的结果非常接近.此外,20世纪60年代地理湖泊所对太湖调查[25]的研究表明,当时太湖总磷浓度在 0.01~0.05mg/L,其中位数为 0.03mg/L,考虑到20世纪60年代太湖的状态良好,受人类活动影响较小,这一调查也支持将 25% 分位点结果作为太湖参照状态浓度.陈奇等[9],张礼兵等[16]关于巢湖参照状态的研究也给出了相近的结果. 表3 25%分位点的值及其95%置信区间估计Table 3 25thpercentile and 95% confidence intervals 表4 参照状态结果Table 4 Reference conditions 先前的研究中关于叶绿素 a参照状态的结果差异较大,郑丙辉等[8]用频率分析法给出太湖叶绿素a的参照状态为4µg/L,高于本研究的结果,这可能是由于太湖在上世纪90年代以来蓝藻的多次爆发,直接导致太湖叶绿素a浓度异常升高,从而引起频率分析法对太湖叶绿素 a参照状态的高估.华祖林等[17]给出的太湖叶绿素 a参照状态浓度为1.81µg/L,置信区间为1.32~2.33µg/L,可以看作是对本次研究结果的支持.另一方面,不同方法建立的巢湖叶绿素 a参照状态结果相差近10倍[9,16],这也表明在这一问题上争议较大,但本研究给出的太湖叶绿素 a参照状态结果在上述研究结果范围内,表明本文给出的结论是可接受的.总之,用25%分位点作为太湖叶绿素a的参照状态浓度是可以接受的.最后,需要注意的是,虽然广义极值分布理论与本文的门限极值理论模型都能够给出太湖总氮、总磷与叶绿素a参照浓度的置信区间.但是,门限极值理论由于能够使用更多的观测值参与建立模型,给出的置信区间精度明显高于广义极值分布理论的结果,这也是门限极值理论的优点之一. 门限极值理论在数学理论与方法更为复杂些,计算的工作量相对也大些,但对于计算机已经十分发达的今天,完全可编制计算程序,快速实现. 4.1 本文基于门限极值模型,提出了一种确定湖泊参照状态浓度的新方法,该方法有效地克服了大部分已有的统计方法无法给出置信区间以及广义极值分布理论对观测数据造成很大浪费的缺点,推断给出模型参数、营养物的参照状态浓度和更为精确的置信区间. 4.2 以太湖为例,建立太湖的总氮、总磷和叶绿素 a观测值的相反数构成的序列,验证了其符合门限极值分理论布:并且和前人结果相印证,说明该方法是可行的.推荐将极值分布统计结果的25%分位点作为太湖参照状态,即太湖总氮的参照状态为0.66mg/L、总磷是0.023mg/L、叶绿素a为 1.27µg/L:它们相应 95%置信区间分别是: 0.55~0.77mg/L、0.022~0.025mg/L、0.84~1.70µg/L,这些置信区间长度都小于广义极值分布理论的结果,这表明门限极值理论在精度上明显优于广义极值分布理论. [1] US EPA. Ambient water quality criteria recommendations:Information supporting the development of state and Tribal nutrient criteria, lakes and reservoirs in nutrient ecoregion II (EPA-822-B -00-007) [R]. Washington, D.C: US EPA, 2000: 6-30. [2] Gibson G, Carlson R, Simpson J, et al. Nutrient criteria technical guidance manual: lakes and reservoirs (EPA-822-B00-001) [R]. Washington, D. C: United States. Environmental Protection Agency, 2000:1-232. [3] Stockner J G, Benson W W. The succession of diatom assemblages in the recent sediments of Lake Washington [J]. Limnology and Oceanography, 1967,12(3):513-522. [4] Walter K D, Robert M O. A technique for establishing reference nutrient concentrations across watersheds affected by humans [J]. Limnology and Oceanography: Methods, 2004,2:333-341. [5] Vighi M, Chiaudani G. A simple method to estimate lake phosphorus concentrations resulting from natural, background, loadings [J]. Water Research, 1985,19(8):987-991. [6] Thèbault J M. Simulation of a mesotrophic reservoir (Lake Pareloup) over a long period (1983 -1998) using ASTER2000biological model [J]. Water Research, 2004,38: 393-403. [7] Walter K D, Edward C, Robert T A. Determining ecoregional reference conditions for nutrients, Secchi depth and Chlorophyll a in Kansas lakes and reservoirs [J]. Lake and Reservoir Management, 2006,22(2):151-159. [8] 郑丙辉,许秋瑾,周保华,等.水体营养物及其响应指标基准制定过程中建立参照状态的方法—以典型浅水湖泊太湖为例 [J].湖泊科学, 2009,21(1):21-26. [9] 陈 奇,霍守亮,席北斗,等.湖泊营养物参照状态建立方法研究[J]. 生态环境学报, 2010,19(3):544-549. [10] 陈 奇,霍守亮,席北斗等.云贵高原湖区湖库总磷和叶绿素a浓度参照状态研究 [J]. 环境工程技术学报, 2012,2(3):184-190. [11] 李小平,陈小华,董旭辉,等.淀山湖百年营养盐化历史及营养物基准的建立 [J]. 环境科学, 2012,33(10):3301-3307. [12] 董旭辉,羊向东,刘恩峰.湖北太白湖400多年来沉积硅藻记录及湖水总磷的定量重建 [J]. 湖泊科学, 2006,18(6):597-640. [13] 董旭辉,羊向东,王 荣,等.长江中下游地区湖泊现代沉积硅藻-总磷转换函数 [J]. 湖泊科学, 2006,18(1):1-12. [14] 董旭辉,羊向东,潘红玺.长江中下游地区湖泊现代沉积硅藻分布基本特征 [J]. 湖泊科学, 2004,16(4):298-304. [15] 顾 莉,李秋兰,华祖林,等.确定太湖流域湖库总磷参照浓度的改进MEI模型 [J]. 湖泊科学, 2013,24(3):347-351. [16] 张礼兵,霍守亮,周玉良,等.基于系统动力学的湖泊营养物基准参照状态研究 [J]. 环境科学学报, 2011,31(6):1254-1262. [17] 华祖林,汪 靓.一种确定湖泊水质基准状态浓度的新方法 [J].环境科学, 2013,34(6):2134-2138. [18] 霍守亮,陈 奇,席北斗,等.湖泊营养物基准的制定方法研究进展 [J]. 生态环境学报, 2009,18(2):743-748. [19] 许秋瑾,朱延忠,郑丙辉,等.我国东部与云贵湖区富营养化控制标准与对比研究 [J]. 中国环境科学, 2011,31(12):2046-2051. [20] Coles S. An introduction to statistical modeling of extreme values [M]. 北京:世界图书出版公司, 2008,45-73. [21] 史道济.实用极值统计方法 [M]. 天津:天津科学技术出版社, 2005:4-65. [22] 秦伯强,胡春华.中国生态系统定位观测与研究数据集—湖泊湿地海湾生态系统卷,江苏太湖站(1991-2006)[M].北京:中国农业出版社, 2010. [23] 苏怀智,王 峰,刘红萍.基于 POT模型建立大坝服役性态预警指标 [J]. 水利学报, 2012,43(8):974-986. [24] 太湖流域水资源保护局.太湖流域及东南诸河省界水体水资源质量状况通报 [R]. 2011. [25] 中国科学院南京地理研究所.太湖综合调查初步报告 [M]. 北京:科学出版社, 1965:37. Estimation of the lake quality reference condition based on the threshold extreme theory. Liang1,2,3, GU Li1,2,3, CHU Ke-jian1,2,3(1.Key Laboratory of Integrated Regulation and Resource Development on Shallow Lakes, Ministry of Education, Hohai University, Nanjing 210098, China;2.National Engineering Research Center of Water Resources Efficient Utilization and Engineering Safety, Hohai University, Nanjing 210098, China;3.College of Environment, Hohai University, Nanjing 210098, China). China Environmental Science, 2014,34(12):3215~3222 A new method was established to calculate the lake nutrient reference condition based on the extreme threshold theory combined with the Peak Over Threshold. The new method not only revealed statistical inferences, but also overcame the weakness such as wasted observational data in generalized extreme value (GEV) theory. More accurate confidence intervals for parameters and substance concentrations could be obtained using this new method. The method was used to estimate the reference conditions of Taihu Lake. The observed data for total nitrogen (TN), total phosphorus (TP) and chlorophylla (Chl-a) at eight sites located in Taihu Lake during 1995~2006 were pre-treated by the Peak Over Threshold. The results revealed that negative values of TN, TP, and Chl-a, which the threshold values are −1.0mg/L,−0.05mg/L, and −4µg/L, fitted the generally Pareto model well. It was recommended to use 25thpercentile as reference conditions. Thus, the values of the reference conditions for TN, TP and Chl-a were 0.66mg/L, 0.023mg/L and 1.27µg/L, respectively. The 95% confidence intervals were also obtained, more accurately than using generally extreme theory. lake water quality criteria;reference condition;threshold extreme theory;confidence intervals X524 A 1000-6923(2014)12-3215-08 华祖林(1965-),男,江苏江阴人,教授,博士,主要从事水环境模拟与污染物质输移机制.发表论文100余篇. 2014-03-08 水体污染控制与治理科技重大专项课题(2012ZX07103-005);国家自然科学基金项目(51379060);江苏省普通高校研究生科研创新计划(CXZZ13_0271) * 责任作者, 教授, zulinhua@hhu.edu.cn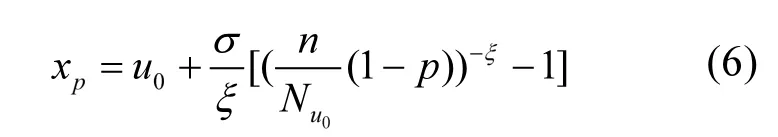
2 数据来源与处理
3 结果与分析
4 结论
HUA Zu-lin1,2,3*, WANG
