正弦量的相量变换方法定义与研究
2014-04-28杨正理
杨正理
(三江学院,江苏 南京 210012)
正弦量的相量变换方法定义与研究
杨正理
(三江学院,江苏南京210012)
摘要:正弦量信号表示为相量的实质是一种时域到复频域的变换关系,但各种教科书及文献并没有对这种变换关系进行严格的变换定义,而只有“表示”方法,因而在应用中带来诸多不便。提出了一种正弦量与相量的数学变换方法即相量变换法,运用严格的数学推导过程证明了这种变换关系的正确性与唯一性,并对其各种性质进行了讨论,分析了这种相量变换法在应用中的便利性,具有较大的推广价值。
关键词:正弦稳态电路;相量法;相量变换法
1 引言
在分析正弦稳态电路时,将正弦信号“表示”为相量(该方法通常称为相量法),就可以采用各种线性电路的定理来分析和求解正弦电路。从数学上的观点来看,正弦量是信号的时域表示方法,而相量是信号的复频域表示方法。所以,当采用正弦量用相量“表示”或将相量“还原”成正弦量的思路,体现了信号在时域与复频域之间的变换关系,是信号在两种域之间的变换与反变换的关系。这种很明显的变换理论,国内外的教科书及文献均没有明确的理论支持和定义,而只说明了正弦量与相量之间仅存在着一种“表示”关系。因缺少相应的系统理论说明,因而往往会影响读者的理解,在分析和解决问题的过程中错误以为两种表示法是同一个概念,难以体会两个域之间的明显区别,产生误解甚至错误。而且由于正弦量既可以用sin函数形式表示,又可以用cos函数形式表示,用相量法表示为相量时其形式不同,在应用时不小心更容易得到错误的结论。
本文明确对正弦量与相量之间的这种变换关系,提出了完整的理论支持,并称其为相量变换法。将正弦量和相量在时域和频域的这种变换和反变换的关系建立在严密数学基础上,并运用严格的数学推导过程证明了这种变换关系的正确性与唯一性。并对其各种性质进行了讨论,分析了这种相量变换法在应用中的便利性,具有较大的推广价值。
2 相量变换法
2.1定义
设有正弦函数想x(t),x(t)既可以是sin函数形式,又可以是cos函数形式,其相量变换均可定义为
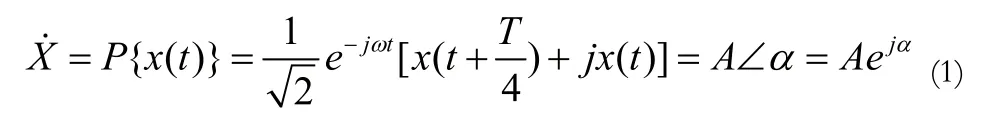

2.2相量变换法的证明
由于正弦量有两种函数形式表示,须分两种情况进行证明。
2.2.1用 函数形式表示正弦量时的相量变换法证明
先证明相量变换,当用 函数形式表示正弦量时,如
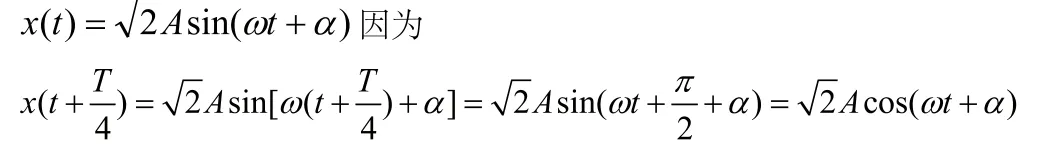
将上式及x(t)代入式(1),得

2.2.2用 函数形式表示正弦量时的相量变换法证明
先证明相量变换,当用cos函数形式表示正弦量时,如

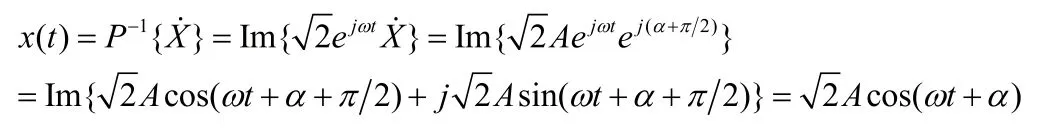
3 相量主要性质讨论
正弦量乘以常数,正弦量的微分、积分及同频正弦量的代数和,结果仍为同频的正弦量,这是正弦量的基本性质。下面采用相量变换法将正弦量的这些基本性质转换为相对应的相量运算。
3.1线性
式中,a,b为常数。
证明如下,

3.2时移(延时)性
证明如下,


3.3微分性
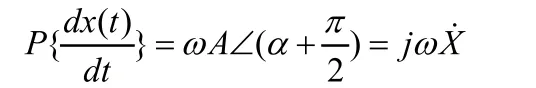
3.4积分性

4 相量变换法在实际应用中的优势
(1)由相量变换法定义知,用sin函数形式表示的正弦量其相量变换结果为:当用cos函数形式表示正弦量时,其相量变换的结果为:;两种不同函数表示形式的正弦量采用相量变换法所得到的结果虽然不同,但因为两种变换结果均由同一数学推导过程得到,虽然应用时增加了一定的繁琐程度,但却不容易混淆。一如两种不同函数表示形式的正弦量具有不同的拉氏变换结果一样,各自具有其对应的结果。
(2)当一个正弦量中既有sin函数形式,也有cos函数形式时,应用相量法表示其相量时需首先对正弦量的函数表示形式进行统一。而当用本文所提到的相量变换法将正弦量变换成相量时,则不要求首先对正弦量的函数表示形式进行统一,而且当得到电路响应结果后,再对响应结果进行反变换时,所得到的正弦量则自动统一为同一类型函数表示形式。这是相量变换法的一个神奇之处。
(3)严格区分正弦量的两种函数表达形式,并区分其在频域的不同变换结果,作者认为是十分必要的。因为在很多实际问题中,正弦量两种表达形式:sin函数和cos函数,很多文献认为其没有区别,具体采用哪一种函数形式,其依据是“该文献的习惯”。将应该有严谨科学定义建立在习惯的基础上,这种提法作者认为是不严谨的。
(4)将正弦稳态电路的相量分析法建立在相量变换法的基础上,由于采用了变换和反变换的数学计算过程,可以有效避免学生因混淆相量和正弦量的区别而导致的一些简单但却常犯的错误,如:
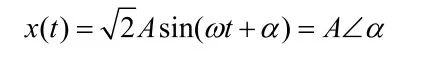
5 应用实例
如图1示,已知输入的正弦电压信号为
求响应i(t)。
解:按定义并结合相量变换的性质,由式(1),u(t)的相量表达式为
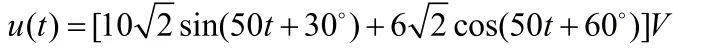
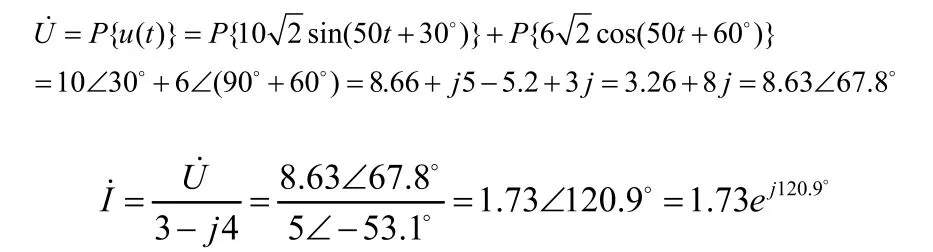
由式(2),得 的正弦量表达式
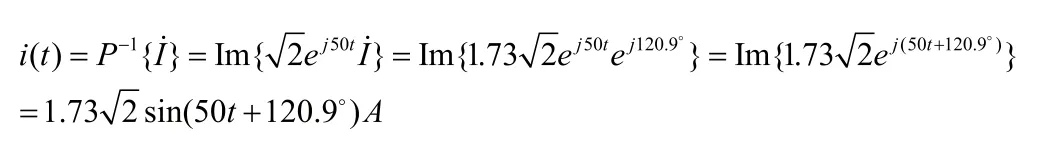
此实例显示,计算时不再需要将正弦量化为统一表达式,且计算过程引入变换理论后更为合理与便捷。
6 结语
将信号的相量与正弦量建立在严密的数学基础上,形成一种严谨的数学变换理论,并在实际应用中体现其应用价值,希望能得到同行们的支持,并能得以推广。这种变换方法在其他领域的应用,也希望同行们共同进行探索。
参考文献:
[1]杨正理.采用小波变换的周界报警信号辨识[J].光电工程,2013(40):84-89.
[2]杨正理等.小波变换在行驶车辆检测器中的应用研究[J].公路交通科技,2013(206):104-108.
[3]杨正理.基于小波变换的模糊C-均值聚类算法在动态汽车衡中的应用[J].自动化仪表,2013(34):73-77.
[4]陈希有,盛贤君,刘凤春.相量与正弦量的数学变换原理[J].电气电子教学学报,2007(02):36-39.
[5]邱关源.电路[M].北京:高等教育出版社(第4版),1999(06).
