考虑相邻档及绝缘子对输电导线找形的影响

谢东周，史庆雪

（沈阳建筑大学 土木工程学院，辽宁 沈阳 110168）

随着我国经济的高速发展，科技的不断进步，对用电量的需求越来越大，依赖程度越来越高，因而国家电网正常运行显得特别重要［1］.但覆冰导线舞动直接威胁着输电线路的稳定与安全，研究覆冰导线发生舞动的原因和找出防止导线舞动的措施具有重要意义.

覆冰导线在静力载荷作用下的形状是输电线路舞动的初始条件，找出其精确求解方法也是一项重要的任务.国内外许多学者对此做了大量的研究工作，张海旺和于建斌［2］用悬链法推导出架空线的弧垂公式，并用ANSYS对导线找形进行了模拟，鲁元兵［3］提出采用V形虚线曲线来对导线进行找形，王丽新和杨文冰等［4］提出了相邻跨对导线找形影响的模型.但他们在研究导线找形时，仅把导线的两端假设为全约束或只把相邻档转化为弹簧单元来约束导线两端，实际上导线的两端不是固定的，其约束条件受到相邻档的跨距、载荷大小、导线的抗拉刚度及连接导线的绝缘子的刚度影响［5］；他们还均把覆冰载荷当作均布载荷布置在导线上，实际上覆冰受到了降雨量、风速、导线的悬挂高度等因素的影响［6］，覆冰厚度也不是均匀的.

本文在相关研究的基础上，考虑相邻档与绝缘子对导线端点约束的影响，并用ANSYS中的APDL语言编写了找出覆冰导线形状的程序，用解析解法验证了程序的可行性.最后笔者研究了不均匀覆冰载荷等因素对导线形状的影响.

1 导线在静力载荷下的数学模型

导线的跨度一般很大，而导线自身的直径比较小，所以导线的抗弯刚度比较小，可以直接把导线等效成柔性索；由于导线的两端受到相邻档距与绝缘子的约束且输电塔的刚度比较大，可以把端部沿导线轴向方向用等效弹簧单元约束，竖直方向看作固定，导线简图如图1所示.

图1 导线的数学模型Fig.1 Mathematical model of conductor

在X轴方向，相邻档及绝缘子对导线端部约束的影响转化为弹簧刚度系数Kx，计算公式如下：

式中，L为相邻输电塔间的覆冰导线总长度；E为导线的弹性模量；A为导线的横截面积；Py为总的竖向载荷强度；Lx为相邻输电塔间覆冰导线水平方向的长度；H 为静拉力的水平分量；Kx1为悬挂绝缘子摆动切线刚度；Li为绝缘子长度；G是为绝缘子的自重；W 为底部作用导线自重及覆冰等垂直载荷；φx为绝缘子与X－Y平面上投影与Y轴夹角.

由于笔者提出的简化数学模型没有考虑导线两端不同高差对导线形状的影响，因此以下计算方法只适用于两端输电塔高差相同的输电导线找形.

2 解析法求输电导线静力形状

2.1 输电导线的悬垂函数

由于导线可以等效成柔性索，因此可以用悬链线法计算输电导线在静力载荷作用下的形状［2］.用悬链线法进行导线静力分析如下：

图2是在初张力（H）及覆冰导线自重载荷作用下导线的形状.如图所示，导线两端离地面的高度相等，P点是导线上任意一点，O点为导线弧垂的最低点，取其为直角坐标系的原点，L为两端点的水平距离，Lx为等效弹簧的拉伸长度.

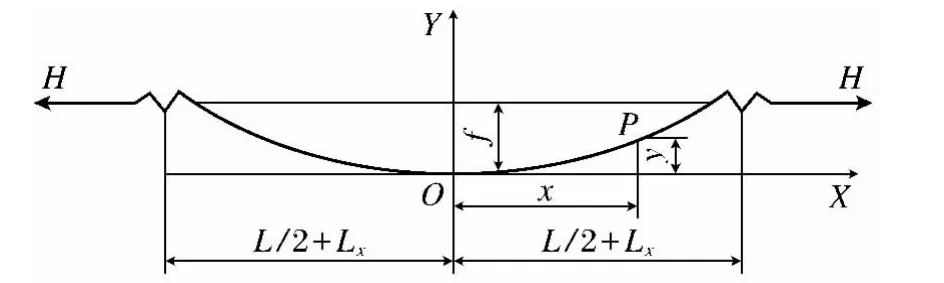
图2 导线悬垂图Fig.2 Diagram of the pendency of conductor

图3是导线OP段的受力图.如图3a所示，OP段导线在H、Lxqx和FP作用下保持静力平衡；图3b是三个静力在P点受力矢量图.

图3 导线OP段受力分析Fig.3 Stress analysis of OPsegment

从图3b中可知，

式中，Lxqy为覆冰导线在OP段的竖向载荷；H为导线的初张力.

对式（4）两端求导得：

由坐标0点可知，x＝0，tanφ＝0，整理得C1＝0，即有

整理并积分得：

为图2所示的输电导线的悬垂函数式.

2.2 输电导线的弧垂

输电导线的弧垂是指从导线上的一点到两端点连线的垂直距离.弧垂的计算公式推导如下：

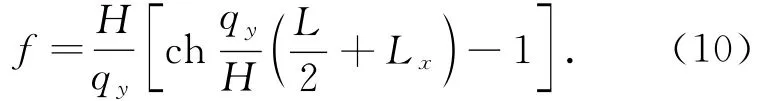
式中，f 为最大弧垂值；Lx＝L1／Kx，L1为相邻导线长度；Kx为端部弹簧刚度.

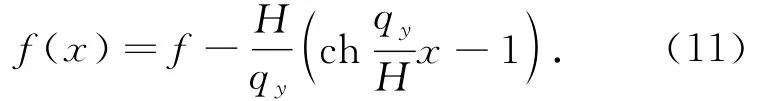
式中，f（x）为坐标点为x的导线弧垂值.

3 导线找形的有限元法

3.1 导线找形分析法的选择

有限元求解导线形状，主要有两种方法，一种是直接迭代法，另一种是找形分析法，它们都能有效模拟出导线的形状［7］.

直接迭代法基本原理是在导线曲弦线位置创建模型，采用实际材料性质和实常数并设置很小的初应变施加自重载荷，沿弧长分布，逐步更新有限元模型，以导线水平张力为收敛条件进行迭代，最终结果即为导线在自重载荷作用下的初始变形.然后施加覆冰载荷，找出导线在覆冰载荷的形状.

找形分析法的基本原理是在架空线曲弦线位置创建模型，采用很大的初始应变和较小的弹性模量，施加自重载荷，其变形即为初始状态的线形.在此线形下恢复实际弹性模量假定很小的初始应变，求得导线在自重载荷作用下的初始状态.然后施加覆冰载荷，找出导线在覆冰载荷的形状.

经比较，找形分析法模拟导线形状更易于收敛，所以本文以找形分析法为基础进行导线覆冰模拟.

3.2 找形分析法的流程

找形分析法的计算流程如下：

（1）选择输电导线模型的单元类型.ANSYS有限元软件中有大量的单元类型可以选择［8］，因此可以很方便地在ANSYS有限元软件中选择输电导线和等效弹簧单元.

输电线路是一种在初拉力和覆冰输电导线自重作用下的柔索结构，在变形时只受拉，不受压.LINK10单元独一无二的双线性刚度矩阵特性，使其成为一个轴向仅受拉或仅受压的杆单元，当选用受拉选项时，受压的刚度就消失，可以模拟导线的松弛；LINK10单元还具有刚度硬化和大变形功能，更和导线的特性相吻合，因此用LINK10单元可以模拟输电导线［9］.

可以用COMBIN14单元模拟相邻导线及绝缘子转化的等效弹簧.COMBIN14单元如图4所示，由于模拟等效弹簧受拉时忽略了阻尼，因此在计算时只需要设置弹簧刚度系数为式（3）计算值.

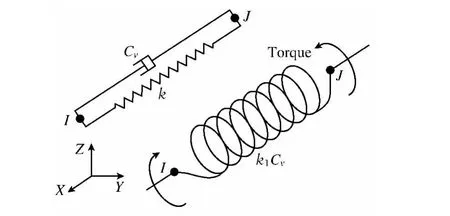
图4 COMBlN14模型Fig.4 COMBlN14

（2）建立导线模型.根据导线的几何参数建立导线的模型，为了便于收敛，假设导线存在着较大的初应变，根据导线的初张力和假设的初应变，计算输电导线假定的弹性模量.

（3）选择合理的求解方法.导线找形是一个典型的大位移小应变的非线性静力问题，所以求解时打开大位移静力和应力刚度选项.

（4）求解初始状态.对上述模型求解，然后恢复导线的真实弹性模量，并设置比较小的初应变，重新求解，即可获得导线在初始状态下的形状.

（5）加冰载荷.以增加导线密度的形式增加覆冰载荷，然后求解，即可获得导线在覆冰载荷作用下的形状.

（6）求解并观察导线位移.提取模型的变形图，即可以得到导线在覆冰载荷作用的形状.

4 数值计算及分析

本文根据《国家电网公司110～500kV输电线路通用设计》规范，选用导线LGJ—630／450，参数见表1，然后选用物理参数如表2所示的绝缘子.

表1 导线物理参数Table1 Physical parameters of conductor

表2 绝缘子的物理参数Table 2 Physical parameters of insulator

为了验证笔者提出简化模型的优越性，先采用不考虑相邻档及绝缘子对导线端部约束影响的传统计算方法［2］对表1与表2的物理参数进行计算.为了与其他计算结果相比较，在水平跨度上每隔25m取一个点，提取出对应点的弧垂，结果如表3所示.

表3 两种方法计算值的比较Table 3 Comparison of the values calculated by two methods

根据笔者推导的悬垂函数式，用Maltab软件编写求解导线悬垂状态的程序.在程序内输入表1与表2的物理参数，求出在导线自重载荷作用下的形状，如图5所示.同样在水平跨度上，每隔25m取一个点，提取出对应点的弧垂，结果如表3所示.

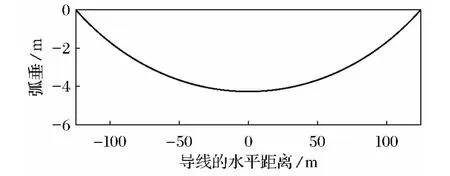
图5 用解析法求解导线的悬垂状态Fig.5 Solving the overhanging state of conductor by analytical method

按照图1所示的简化模型，用ANSYS有限元软件模拟输电导线在自重载荷作用下形状，导线的变形如图6所示，同样在水平跨度上每隔25 m取一个点，提取出对应点的弧垂，结果如表3所示.

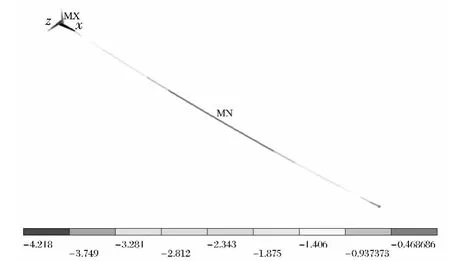
图6 用有限元法求解导线的悬垂状态Fig.6 Solving the overhanging state of conductor by finite element method

从表3可知，在计算同一条导线的弧垂时，不考虑相邻档导线及绝缘子对导线端部约束影响的传统计算方法计算的值比考虑相邻档导线及绝缘子对导线端部约束影响的新计算方法计算的值要小，由于新计算方法的数学模型更符合导线端部约束的情况，其计算值更符合实际，说明传统计算方法计算的值要小于导线实际情况的弧垂值，从而体现了新计算方法的优越性.

从表3还可以知道，考虑相邻档导线及绝缘子对导线端部约束影响时，解析法及有限法计算导线各点弧垂值的最大相对误差为5.7%，显示出用有限元方法计算导线找形的有效性.

5 覆冰载荷的变化对导线找形影响的研究

导线覆冰是形成导线舞动的必要条件，所以探讨导线的覆冰情况对导线在静力作用下形状的影响是有必要的.

5.1 覆冰载荷等效均匀分布

为了计算方便，通常有限元法计算导线的形状时，认为导线覆冰载荷是均匀分布.本节在导线自重找形的基础上加载12N／m的均匀覆冰载荷，求解时打开大变形瞬态选项，在通用后处理器（POST1）中提取在覆冰载荷作用下导线的变形图，如图7所示.从图中可知导线的最大弧垂是－4.72m，出现最大弧垂的位置距端点125m，即跨中.

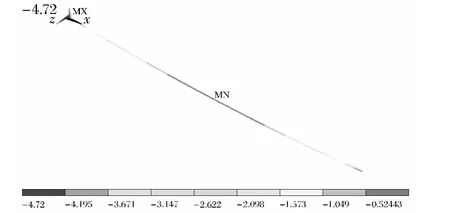
图7 覆冰导线找形后的悬垂状态Fig.7 Hanging state of iced conductor's shape after form－finding

然后在时间历程后处理器（POST26）中提取跨中点的位移时程历程图，如图8所示，从图中可知，导线在保持自重形状时，突然受到冰载荷，导线的弧垂会急剧下降，当冰载荷稳定以后，导线的弧垂有所恢复，但弧垂还是增了0.7m（－4.9－（－4.2）），所以在研究导线变形时，不可忽略冰载荷对形状的影响.

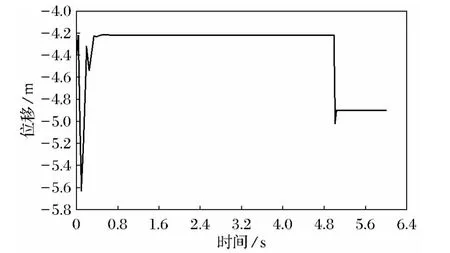
图8 导线在外载荷作用位移反应时程Fig.8 Conductor's displacement responses time course to external loads

5.2 不均匀覆冰对导线变形的研究

在传统研究中，常把导线的覆冰载荷等效成均布载荷，但实际情况中结冰厚度受到了导线的悬挂高度、风速、气候条件的影响，在一个导线中，冰的厚度是不均匀的，所以考虑不均匀覆冰对导线形状的影响是必要的.

笔者用六条不同覆冰导线来探讨不均匀覆冰载荷对导线静力找形的影响 ，具体研究方案如下：

把每条导线的水平跨度分成五段，每段长度为50m，从导线的左端起，依次取名A、B、C、D、E段，在每个区段施加不同的覆冰载荷，但保持每条导线的冰载荷总和相等.各条导线冰载荷布置如表4所示.

表4 各条导线覆冰载荷分布Table 4 Distribution of ice loading of individual conductors N／m

用ANSYS有限元软件分别计算各条导线在覆冰载荷下的形状，提取各导线的最大位移与出现最大位移的点，结果如表5所示.

从表5可知，与均匀覆冰最大弧垂相比较，当较大覆冰载荷集中在导线两端时，不均匀覆冰的最大弧垂小于均匀覆冰的最大弧垂，但差值不大；当导线较大覆冰载荷值集中在跨中但较大载荷与端部载荷差值不大时，不均匀覆冰的最大弧度与均匀覆冰的最大弧垂差值也不大；当导线较大覆冰载荷值集中在跨中且其值远大于端部覆冰载荷时，最大弧垂会出现很大的差值.因此覆冰载荷不均匀差值比较小，或者较大覆冰载荷集中在导线两端，可以把导线的覆冰载荷等效成均匀覆冰载荷来计算导线的形状，但当覆冰载荷差值比较大且较大载荷集中在跨中，要考虑不均匀覆冰对导线形状的影响.

表5 不同导线位移的比较Table 5 Comparison of displacement of different conductors

与均匀覆冰最大弧垂出现的位置相比较，当不均匀覆冰载荷对称布置时，最大弧垂会出现在跨中，即与均匀覆冰最大弧垂出现的位置相同；当不均匀覆冰载荷不是对称布置时，最大弧垂的位置会往载荷较大端偏移，偏移的大小受到载荷偏移程度的影响.

6 结 论

（1）考虑相邻跨及绝缘子对导线端部约束时，模拟值与理论值非常接近，其结果误差不仅能满足工程中对导线形状的控制要求，而且可以作为研究导线舞动的初始条件.

（2）当不均匀覆冰载荷差值比较小，或者较大覆冰载荷集中在导线两端，可以把导线的覆冰载荷等效成均匀载荷来计算导线的形状；当覆冰载荷差值比较大且较大载荷集中在跨中，要考虑不均匀覆冰载荷对导线形状的影响.

（3）在估算导线最大弧垂出现位置时，应考虑导线覆冰的不均匀影响，当覆冰载荷均匀分布或者对称分布时，最大弧垂会出现在导线的跨中；当导线覆冰载荷不均匀分布时，导线的弧垂向较大载荷端偏移.

［1］ 赵羡龙，李晓林.智能电表在智能用电中的重要作用［J］.沈阳大学学报：自然科学版，2012，24（6）：26－29.

（Zhao Xianlong，Li Xiaolin.Important Role of Intelligent Electric Meter in Intelligent Power Consumption［J］.Journal of Shenyang University：Natural Science，2012，24（6）：26－29.）

［2］ 张旺海，于建斌.基于ANSYS的架空输电导线找形研究［J］.电力建设，2012，33（2）：32－35.

（Zhang Wanghai，Yu Jianbin.Form－Finding Analysis of Overhead Transmission Line Based on ANSYS［J］.Electric Power Construction，2012，33（2）：32－35.）

［3］ 鲁元兵.输电线路覆冰脱落及断线分析［D］.杭州：浙江大学，2010：23－24.

（Lu Yuanbing.Iced－Shedding and Wire－Breaking Analysis of Transmission Line System［D］.Hangzhou：Zhejiang University，2010：23－24.）

［4］ 王丽新，杨文兵，杨新华，等.输电线路舞动的有限元分析［J］.华中科技大学学报：城市科学版，2004，21（1）：76－80.

（Wang Lixin，Yang Wenbing，Yang Xinhua，et al.Finite Element Analysis for Galloping Process of Transmission Lines［J］.Journal of Huazhong University of Science and Technology：Urban Science，2004，21（1）：76－80.）

［5］ Mathur R K，Shah A H，Trainor P G S，et al.Dynamics of a Guyed Transmission Tower System ［J］.Power Delivery，IEEE Transactions on，1987，2（3）：908－916.

［6］ 李宏男，李雪，李钢，等.覆冰输电塔－线体系风致动力响应分析［J］.防灾减灾工程学报，2008，28（2），127－134.

（Li Hongnan，Li Xue，Li Gang，et al.Wind－Induced Dynamic Response Analysis of Iced Transmission Tower－Line System ［J］.Journal of Disaster Prevention and Mitigation Engineering，2008，28（2）：127－134.）

［7］ 孔伟，朱明伟，付豪.架空输电线路导线在ANSYS中的找形分析［J］.东北电力大学学报，2011（Z1）64－67.（Kong Wei，Zhu Mingwei，Fu Hao.The Find－forming of Transmission Line in ANSYS［J］.Journal of Northeast Dianli Uiniversity，2011，33（2）：64－67.）

［8］ 曾支明，丛树民.框架－剪力墙结构高层地震问题的数值分析［J］.沈阳大学学报，2011，23（6）：118－120，124.

（Zeng Zhiming，Cong Shumin.Numerical Analysis on Frame－shear Wall Structure High－rise Buildings under Earthquake［J］.Journal of Shenyang University，2011，23（6）：118－120，124.）

［9］ 王新敏.ANSYS工程结构数值分析［M］.北京：人民交通出版社，2004：158－189.

（Wang Xinmin. Numerical Analysis of Engineering Structure in ANSYS［M］.Beijing：China Communications Press，2004：158－189.）