复合式镗铣加工中心滑枕变形分析与补偿研究*

舒启林 崔世超 鑫 龙

(沈阳理工大学机械工程学院，辽宁 沈阳110159

复合式镗铣加工中心是我国自主研发的高档加工中心之一，该镗铣加工中心具有高精、高效、高稳定性的特点，适于加工精密复杂的箱体类工件。该镗铣加工中心的镗削主轴箱沿着立柱上下移动，滑枕安装在主轴箱的滑台上，其中滑枕的最大行程是1 200 mm。在镗削过程中，滑枕将成为悬臂式的工作部件，由于滑枕的自身与主轴总成等附件的重力因素，使得滑枕在伸出过程中必然会产生一个向下的挠曲变形，称为“滑枕低头”现象，这种挠曲变形破坏了镗铣加工中心的几何精度，而且引起了加工误差［1-2］。因此，为了保证加工精度，必须采取适当的措施对滑枕挠曲变形进行补偿。

目前，国内外对滑枕挠曲变形的补偿措施主要采用机械式修正法和数控软件修正补偿，这些措施对滑枕的非线性变形的改善效果却不理想。文献［3］提出一种采用预应力挠曲变形的结构设计，将滑枕因自重变形超出理想形状的那部分材料去除掉，从而使滑枕在行程中处于平直状态，该方法能够得到一定的补偿效果，但没有考虑到因更换刀具时由装刀部件重量变化引起的变形量改变，以及对滑枕本身的加工与装配要求较高。文献［4 -5］提出一种通过机床的数控系统实现滑枕的挠曲变形补偿方法，该方法利用数控系统通过控制Y 轴上升相应的位移来实现误差补偿，但它仅补偿因重力引起的挠度，并未补偿滑枕的弯曲变形。文献［6］提出一种电液比例控制法对滑枕挠曲变形进行补偿，取得了一定的补偿效果，但该法需要准确把握滑枕各个阶段的变形函数，对于快速移动的滑枕会出现响应滞后的现象。文献［7］提出一种滑枕分段补偿法，该法在滑枕的前半部安装推杆，在滑枕的后半部安装拉杆，虽然能够较好地补偿滑枕的角度摆动误差，但控制过程很难实现。

本文以复合式镗铣加工中心为例，研究其滑枕挠曲变形误差及补偿问题，提出一种液压拉杆的补偿方法，利用有限元分析的方法得到滑枕挠曲变形的分布规律，以及滑枕的变形量与滑枕行程之间的关系曲线;通过理论分析得出拉杆补偿力的初算值，再结合有限元分析与多项式最小二乘法拟合得到拉杆补偿力与滑枕行程的函数关系及函数对应的曲线。

1 复合式镗铣加工中心介绍

复合式镗铣加工中心是将卧式镗削结构与龙门铣削结构相结合的结构布局，其主要部件如图1 所示。该加工中心具有铣削和镗削两个主轴，可以对大型复杂箱体类工件实现一次装夹多面的复合加工，避免了由于多次装夹造成的精度下降现象，且大大提高了加工效率。

镗削系统是复合式镗铣加工中心的关键系统，在镗削加工过程中，滑枕伸出形成悬臂状态对工件进行加工，在滑枕自身及内部主轴总成重力的作用下，滑枕会产生一个向下的挠曲变形，进而影响了镗削的加工精度。

2 滑枕的变形分析

滑枕在复合式镗铣加工中心中起到连接主轴箱和主轴的作用，滑枕部件的三维实体如图2 所示。滑枕整体外形为长方体，底面有两根导轨，内部安装主轴总成，滑枕端面尺寸274 mm×265 mm，总长2 540 mm，Z轴行程1 200 mm，材料为灰铸铁HT300，弹性模量E=157 GPa，密度ρ=7 350 kg/m3，泊松比μ=0.23。

滑枕是装配在主轴箱内，通过滑动导轨在主轴箱内横向运动，滑枕所受的载荷主要来自自身的重量和内部主轴总成的重量，滑枕在伸出过程中必然会产生挠曲变形。复合式镗铣加工中心滑枕的最大行程为1 200 mm，滑枕的挠曲变形将随着滑枕行程的变化而产生非线性变化。以主轴实体端面中心为基准，在0～1 200 mm 的行程范围内，以每100 mm 行程取点，总共选取12 个位置进行有限元静力分析，可得出滑枕在不同行程时各方向上的最大变形量如表1 所示，当滑枕行程为1 200 mm 时的综合变形云图如图3 所示。

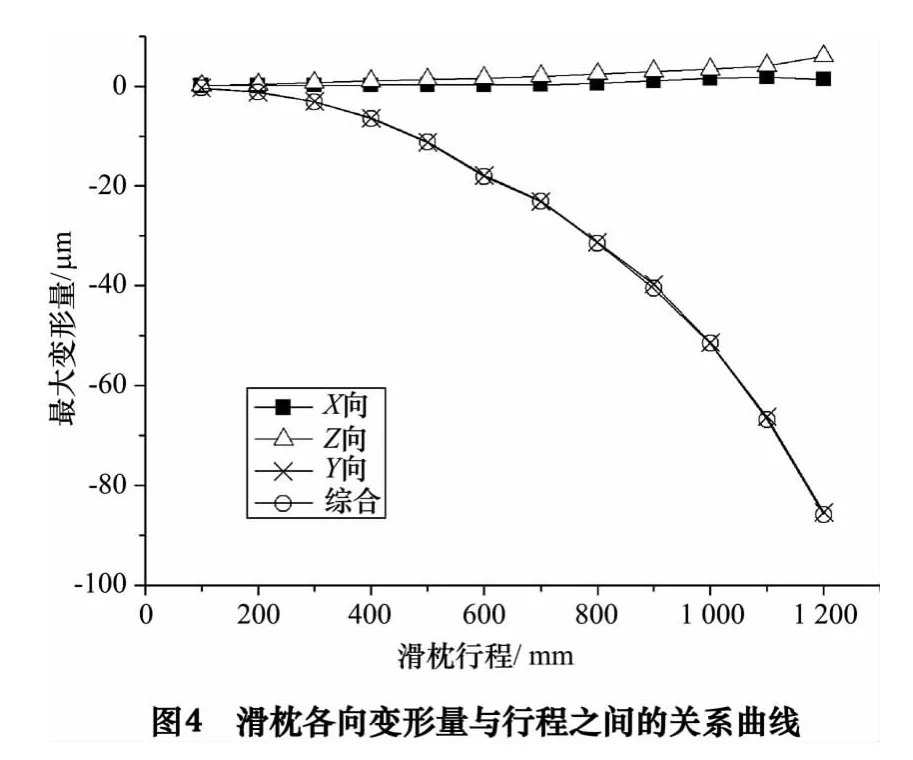
对表1 中的数据进行拟合处理可得到滑枕挠曲变形量与滑枕行程间的关系曲线如图4 所示。从分析结果得知滑枕行程为1 200 mm 时，滑枕的最大综合变形量为-86.06 μm，其中Y 向变形为-85.85 μm，Z 向变形为5.98 μm，X 向为1.35 μm。从图4 可以看出，随着滑枕伸出量增加，X 向的变形量不大，Z 向变形量也不大，但Y 向变形量和综合变形量很接近，这说明滑枕的变形主要是由滑枕及主轴总成自重引起。国家机械行业标准［8］规定，镗铣床滑枕应满足0.02 mm/500 mm 的精度要求。本文研究的滑枕行程在700～1 200 mm 范围内时，滑枕变形量已远远超标，所以滑枕挠曲变形补偿显得尤为重要。

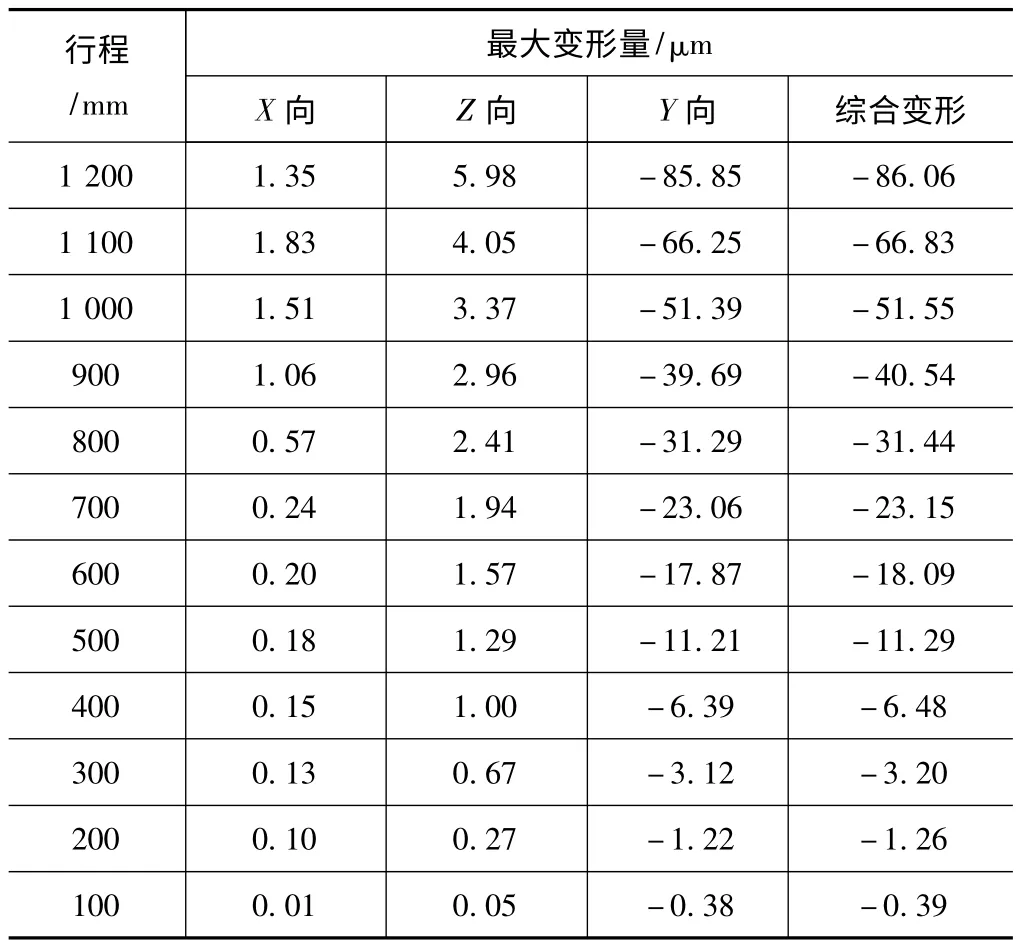
表1 滑枕各行程各方向最大挠曲变形量

3 挠曲变形补偿措施

3.1 补偿装置结构

滑枕挠曲变形是由重力作用引起。因此，补偿的基本思想:为了平衡掉由于重力作用引起的弯曲变形，施加一个外载来平衡掉这个弯曲变形，从而实现挠曲变形补偿。

基于上述思想，本文采用液压拉杆力补偿法对挠曲变形进行补偿。具体措施是:在滑枕内部上方安装两个细长拉杆，拉杆的拉力由液压油缸提供，通过调整拉力来补偿滑枕的挠曲变形，拉杆及油缸的安装如图5 所示。

3.2 补偿原理分析

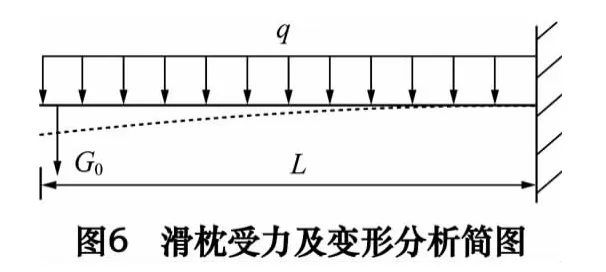
由于滑枕的挠曲变形是由自身及内部主轴总成重量引起的，所以可将滑枕的受力情况化简为方截面直梁受力［9］，将滑枕自身重力简化成均布载荷q，前端主轴总成重力为G0，则滑枕的受力及变形情况可简化为图6 所示。

实施挠曲变形补偿时，滑枕的受力如图7 所示。其中，F1和F2为两个拉杆的拉力，产生偏心压缩的效果;e 为拉杆力作用点到滑枕中心的距离;θ 为拉杆中心到滑枕中心连线与滑枕中性层的夹角。

为了保证滑枕悬伸时主轴端面中心的挠曲变形量为最小，则需要拉杆的拉力产生的挠度与滑枕本身挠度方向相反、大小相等。即

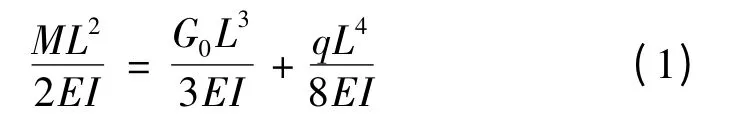
式中:M 为拉杆力所产生的力矩;E 为滑枕材料的弹性模量;I 为滑枕截面的惯性矩;L 为滑枕的伸长量。

由于两个拉杆上的拉力相等，设F1=F2=F，所以补偿力F 产生的力矩M 可表达为:

(2)拉杆安装的位置确定后，θ 和e 也随之确定，将式(2)带入式(1)中得:

3.3 补偿力的确定

利用Solidworks 三维建模软件的估算模块，分别得出未知量，q=2.5 kN/m;G0=3.5 kN;当滑枕伸出最大行程L=1 200 mm 时，将其参数带入式(3)中，可得滑枕行程为1 200 mm 时，所需补偿力的计算初始值。

同理，算出滑枕在500～1 200 mm 的8 个不同行程时补偿力的初始值，利用有限元的方法对滑枕施加拉杆补偿力后的变形分析，可得到滑枕挠曲变形补偿后的变形量。根据分析结果对补偿力的初始值进行修正，直至滑枕的挠曲变形量满足要求为止，补偿力的数据如表2 所示，图8 为补偿后滑枕行程1 200 mm 时的综合变形云图。

表2 各个行程时的补偿力数值

由图8 可知，挠曲变形补偿后滑枕在最大行程时的最大挠曲综合变形量仅为-9.94 μm，相对补偿前的-86.06 μm 变形量，补偿后的变形量值减小88.44%，完全满足了机械行业国家标准规定的镗铣床滑枕的精度要求，且使得在整个行程范围内滑枕的挠曲最大变形量都在10 μm 之内，补偿前后滑枕的挠曲综合变形量对比如表3 所示。

表3 挠曲变形补偿前后的最大变形量对比

3.4 拉杆补偿力拟合曲线

最小二乘法是一种常见的工程问题处理方法，常用于从一组实验数据(xi，yi)(i=0，1，2，…，m)中寻找自变量x 与因变量y 之间的函数关系。

且使得总误差Q 达到最小。

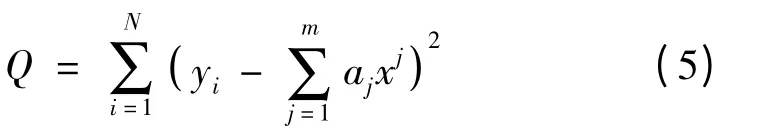
此时，Q 可视为关于aj(j=0，1，2，…，m)多元函数，所以式(5)的系数求解问题可以转化为以aj(j=0，1，2，…，m)为变量的多元函数极值问题，可得如下正则方程组(m=0，1，2，…，m)

该正则方程组的解即为式(4)中的系数，且这组解存在唯一值［10］。因此，对表2 中的数据做多项式最小二乘法拟合，采用三次多项式最小二乘法拟合得到拉杆补偿力F(kN)与滑枕行程量L(mm)的函数关系为:

根据上述函数关系，做出拉杆补偿力与滑枕行程的关系曲线如图9 所示。从图可以看出，拉杆补偿力与滑枕行程量的关系曲线变化平稳，液压系统能够很好地实现补偿力的施加。在装配的实际调试中，如果按照过去的方式，只能依靠反复的试验来寻找合理的补偿力的初始值。但是借助有限元分析和理论计算的方法，很准确地找到补偿力的合理值。

4 结语

(1)通过有限元分析方法得到了复合式镗铣加工中心滑枕挠曲变形随行程的变化规律，得到滑枕在最大行程时的最大挠曲变形量为86.06 μm，为滑枕挠曲变形补偿提供了量化依据。

(2)拉杆补偿机构安装在滑枕内部，最大限度的减小了对滑枕的运动影响，通过机床的数控系统与伺服电液比例阀相结合，避免了附加其他复杂的控制系统。

(3)拉杆补偿力可实现从零到最大补偿力的无级加载，加载补偿力后将最大的挠曲变形控制在10 μm之内，显著提高了机床的加工精度。

(4)通过有限元仿真分析和数值计算相结合的研究方法，较好地解决了复合式镗铣加工中心滑枕的挠曲变形难题，减少调试阶段的大量实验工作，提高了产品的开发效率，对机床的变形分析及补偿研究具有良好的参考价值。

［1］Schwenke H，Knapp W，Haitjema H，et al.Geometric error measurement and compensation of machines—an update［J］.CIRP Annals -Manufacturing Technology，2008，57(2):660-675.

［2］Uriarte L，Zatarain M，Axinte D，et al.Machine tools for large parts［J］.CIRP Annals-Manufacturing Technology，2013.

［3］戴晨，刘小鹏，张文桥.TK6916B 数控落地铣镗床补偿系统分析［J］.湖北工业大学学报，2007，22(4):4 -5.

［4］王洪才.数控铣镗床滑枕下垂补偿系统［J］.制造技术与机床，2003(6):24 -25.

［5］杨志伟，吕东杰.用PC 软件实现滑枕低头自动补偿［J］.一重技术，1998，37(1):1 -5.

［6］Mahbubur Rahman，Jouko Heikkala，Kauko Lappalainen.Modeling measurement and error compensation of multi-axis machine tools［J］.International Journal of Machine Tools and Manufacture，2000，40(4):1535 -1546.

［7］孙德洲.滑枕下垂变形的分段补偿方法［J］.组合机床与自动化加工技术，2008，50(6):77 -83.

［8］中华人民共和国机械工业部.JB/T8490.1 -96.数控落地铣镗床、落地铣镗加工中心精度检验［S］.北京:中国标准出版社，1997.

［9］吴凤和，王少伟，杨育林，等.超重型数控落地铣镗床滑枕挠曲变形补偿研究［J］.中国机械工程，2010，21(20):2416 -2420.

［10］李庆扬，王能超，易大义.数值分析［M］.武汉:华中科技大学出版社，2006:64 -76.