深水管道弃置回收非线性受力分析及其形态控制

毛东风，苏宁宁，段梦兰，张来斌，李志刚

(1.中国石油大学海洋油气研究中心，北京102249;2.中国石油大学安监总局油气安全工程技术研究中心，北京102249;3.海洋石油工程股份有限公司，天津300451)

铺管船法是深水油气管道唯一的铺设方式。铺设中当遭遇极端气候条件或铺管船出现严重事故，或者运管船在一定恶劣海况下因不具备动力定位能力无法工作时，将终止作业并暂时将管线下放至海底，待海况转好或故障排除后，再将管线回收至铺管船继续铺设。目前世界铺管作业水深已发展到3000 m，而中国相应的工程作业能力仅在200 m水深范围。在海洋油气丰富的南海，已经发现的油气区块均在中等水深(1000 m)以上，潜在的油气区块水深将达3000 m。研究深水管道铺设的关键技术，对于工程设计和快速可靠地安全施工、提升中国深水管线作业能力具有重要意义。因此，笔者采用弹性地基板理论和非线性梁理论分别建立弃置回收作业中深水管道触底段和悬跨段几何大变形管道模型，分析其力学行为。

1 国内外研究现状

关于正常铺设管道的应力与变形分析，国内外学者提出了许多方法，大都集中在数学模型的求解上，如悬链线法［1］、摄动法［2］、有限差分法［3］、非线性有限元法［4］等。Kimura等［6］将管道当作连续梁，给出同时考虑弹塑性和几何非线性的分析式及其解析解和数值解。詹侃等［7］将管道在铺设过程中的二维静态问题处理成非线性大变形两点边值问题，应用逐步积分法进行求解。Plunket和Brewer等［8-9］采用刚悬链线法，将边界条件的影响限制在末端“小边界层”。Powers等［10］考虑不同边界条件及沿管道载荷变化等复杂情况，采用有限元法和初值渐次逼近法求解管道铺设中的二维问题。帅健等［11］采用动坐标迭代法判断有限元求解过程中管道是否与海床接触。

目前，对于弃置回收作业中管线的分析较为少见。Datta［4］建立了弃置和回收作业过程中管道的平衡微分方程，采用有限差分法分析管道的变形和受力。

弃置回收作业中的管道存在很长的悬跨段，作业中绝大部分时间内无上弯段，形态与J型铺设类似，具有非线性大变形的特点。由于管道上端与A＆R绞车缆绳连接，上部边界条件与正常铺设不同。因此，前述正常铺管时的受力分析方法均有一定程度的不足。鉴于此，本文中考虑底部边界海床土壤地基、海流(包括测向流)等环境因素的影响，对弃置和回收作业中的管线进行大变形非线性有限元分析。

2 深水管道弃置和回收作业非线性受力的理论分析

2.1 管道力学模型

弃置回收作业中的管道分为触底段和下弯段两部分，AB段为A＆R绞车缆绳。载荷包括:A＆R绞车拖拉力F，静水压力，管道与土壤地基的接触反力FX、FY，波流力 f，单位长度管道湿重 w 等，见图1。

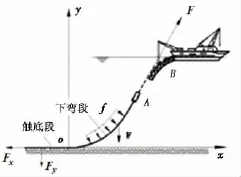
图1 弃置回收作业管道的受力Fig.1 Forces on pipeline in abandonment and recovery operation

2.2 触底段

将触底段视为置于均质弹性土壤基础上的梁。土壤地基选用Pasternak模型。触底段微元受力见图2。

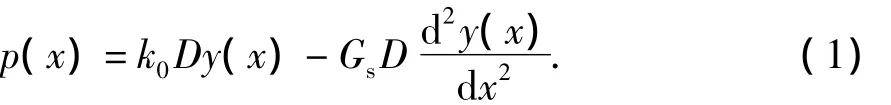
式中，p为地基反力，N;k0为地基反应模量，N/m2;D为管道外径，m;Gs为土壤剪切模量，N/m2。

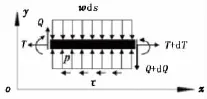
图2 触底段微元受力Fig.2 Forces acting on pipe element in touchdown segment

设管土间摩擦力τ沿管长均匀分布，由平衡条件得到控制方程为T满足边界条件:

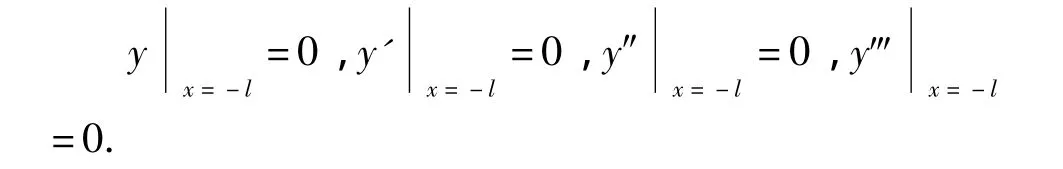
式中，T为管道轴向拉力。

2.3 悬跨段

悬跨段微元受力见图3。采用大挠度梁理论，由平衡微分方程及挠曲微分方程得到控制方程为

初始构形与自然悬链线近似。悬跨段的边界条件为上端与A＆R绞车缆绳相连。触地点须考虑土壤对管道的作用。将DnV规范与土样调查数据结合，得到土壤对管道单位长度在垂向、侧向、轴向3个方向的反力［12-13］。

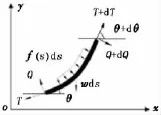
图3 悬跨段微元受力Fig.3 Forces acting on pipe element in spanning section

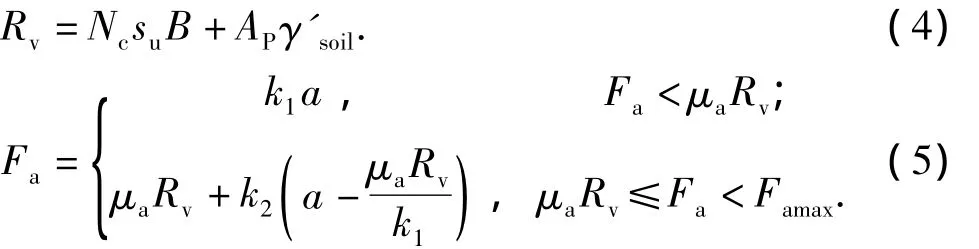
假定土壤对触底段管道的摩擦力沿管道轴向均匀分布。

其中

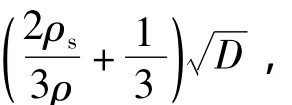
式中，Rv和Fa分别为土壤单位长度垂向反力和侧向反力，N/m;τ为单位长度管道受到的轴向摩擦力，N/m;B 为管土接触宽度，m;γ′soil为土壤容重，N/m3;AP为管道入泥部分的横截面积，m2;Nc为土壤承载力系数，取5.14;su为土壤不排水抗剪强度，kPa;a为侧向入泥深度，m;μa和μ1分别为土壤侧向和轴向摩擦系数，对于黏土，分别取0.2和0.1～0.3;k1、k2为土壤等效刚度，N/m;Ca为土壤动态刚度系数;μ 为土壤泊松比;ρs/ρ取 1.2 ～2;γsoil为土壤总单位重力，N/m3;γwater为水的单位重力(10 kN/m3)。

2.4 理论方法及参数选取

采用Morison理论计算悬跨段管道受到的波流力作用［14-16］。

其中

式中，ρwater为海水密度，kg/m3;CM为惯性系数;CA和CD分别为附加质量系数及阻力系数;u为水质点速度，m/s。

认为目标管道表面光滑度较高，结合DnV和API等相关规范，CD、CM分别取0.7和1.8。

3 非线性数值模拟分析

3.1 管道形态控制

3.1.1 模型

目标管道穿越海域水深5～1 500 m。其中有3条深水管线:两条SSTB主管道和一条MEG管道，均由1390 m水深的PLEM/SDH回接到水深200 m的SWH浅水平台。管道主要参数见表1。土壤地基参数:不排水抗剪强度su、泊松比、单位土壤重力γsoil、土壤侧向、轴向摩擦系数、土壤侧向动态刚度系数分别为 11.5 kPa、0.45、8 kN/m3、0.2、0.3 和 500 kN/m5/2。上述土壤参数根据部分实测土壤参数和DNV-RP-F105中软黏土指导参数选取。

表1 管道数据Table 1 Pipeline data

3.1.2 结果分析

对于SSTB主管道(表2)，提升角 θ＞87°时管线最大应力σmax大于管线许用应力，θ≤87°时，σmax开始小于管线的许用应力。θ=89°～80°时，触地点管线曲率半径较小，σmax一直出现在该处，且随提升角的减小而减小。θ=80°～66°时σmax位置从底端逐渐向提升端转移，其值逐渐减小。θ=62°～54°，σmax位于提升端，但随θ减小而有所增大。提升力则随θ的减小而增大;θ=53°，提升能力为351.04 t，开始超过给定的拖拉能力350 t。由此可以确定提升角的合理取值范围应为88°～54°。考虑计算误差，建议提升角控制在85°～60°。

图4 海管悬链线模型Fig.4 Catenary model of pipeline

表2 SSTB主管道计算结果Table 2 Calculated results for SSTB main pipe

对于MEG管道(表3)，提升角 θ≤89°时，σmax=283.90 MPa，开始小于管线的许用应力，直至θ=80°时σmax一直出现在管线底端，并且逐渐减小。当θ＜80°时，σmax开始出现在提升端，并随θ的减小而略有增大，θ=30°时，σmax=384 MPa，又开始大于管线许用应力。当θ=89°～31°时，提升力小于给定的拖拉能力。由此可确定提升角的合理范围为89°～31°。同样考虑计算误差，建议提升角控制在86°～40°。

3.2 管道非线性静力有限元分析

考虑弹性海床、波流的影响，研究SSTB主管道提升至托管架末端时的受力状况。触底段长度取500 m。重现期为1 a时，有效波高为8.7 m，平均跨零周期为8.5 s，最大波高为16.2 m，最大波周期为12.4 s;重现期为100 a时，有效波高为15.0 m，平均跨零周期为10.4 s，最大波高为28.0 m，最大波周期为15.2 s。

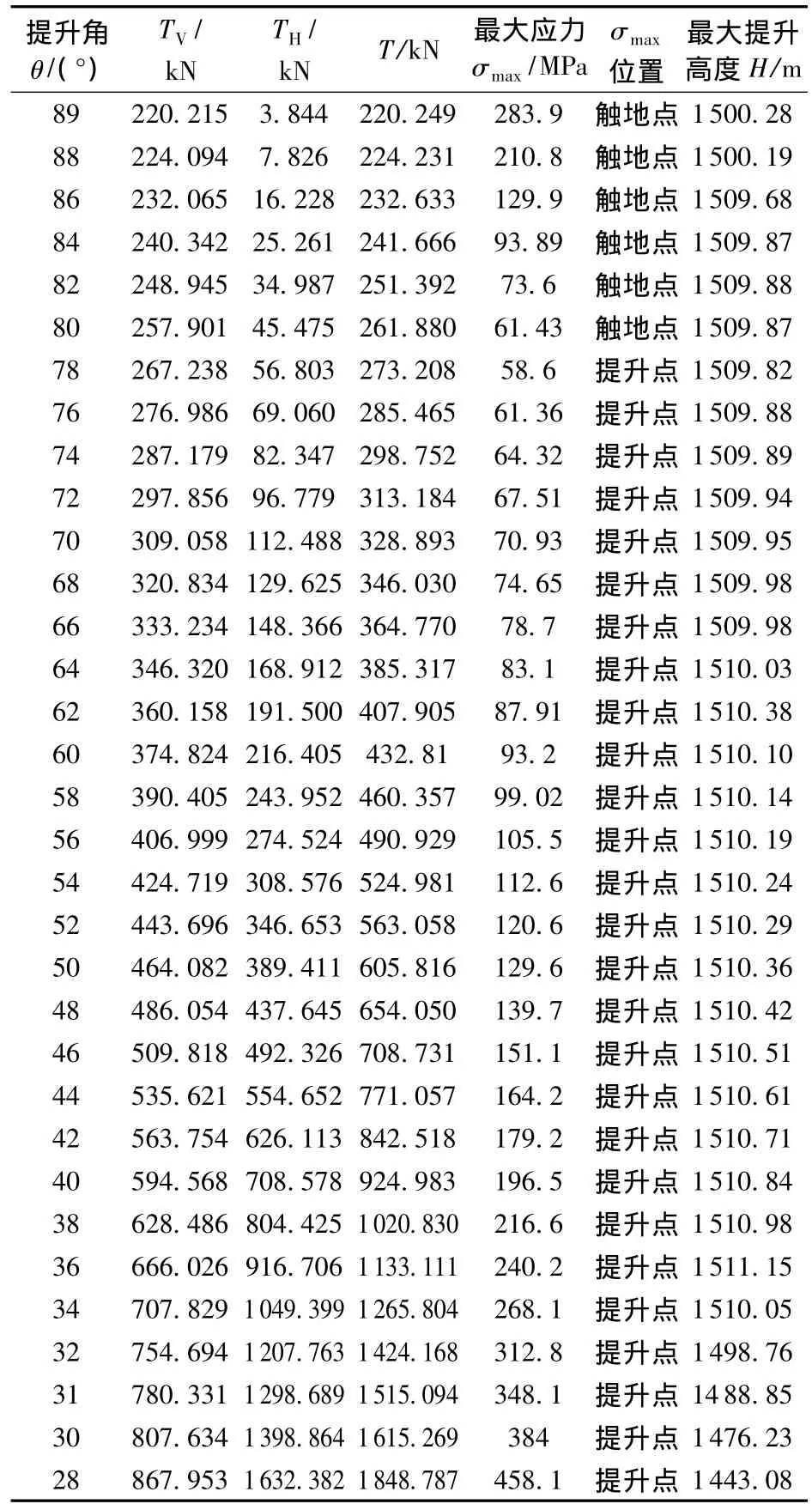
表3 MEG管道计算结果Table 3 Calculation results of MEG pipeline

表4 垂直剖面设计流速Table 4 Design flow rate in vertical section

图5、6为不同提升角时无波流力及顺流、侧向流、逆流对SSTB主管道弃置回收作业时受力的影响。可以看出，无波流力时，距海床越高管道上轴向拉力越大;提升角越小，轴向拉力越大，θ=85°、70°、60°时的最大值分别为1.426、1.962和2.593 MN。这些数据说明进行深水管道弃置回收作业时，采用较大提升角可以大幅减小A＆R绞车负荷，保证系统设备安全。但是过大的提升角将导致管道顶端的应力水平较高。因此建议提升角选择80°～82°。

图5 悬跨段管道轴向拉力/应力随水深的分布Fig.5 Axial tension/stress distribution of spanning section along depth

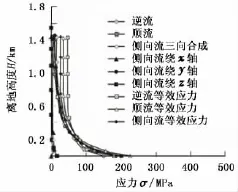
图6 不同方向海流作用下悬跨段管道应力分布Fig.6 Stress distribution of spanning section under different currents

θ=80°时，顺流下管道轴向拉力最大，即A＆R绞车负载最大;逆流时轴向拉力最小。这是因为逆流有使管道提升角增大的趋势。3种流向下提升点处轴向拉力最大值分别为1.568、1.460、1.519 MN。一般情况下，深水铺管船用A＆R绞车设计安全系数≥2，因此A＆R绞车的拖拉能力需要达到3.136 MN以上。顺流和逆流下管道弯曲应力的变化趋势相似，因为顺流和逆流时，理论上管道只有绕y轴的弯矩，主要由管道重力和静水浮力所致。而侧向流的作用会导致3个方向的弯曲应力，且x、z轴方向的较之y轴的要小很多。管道等效应力主要取决于弯曲应力。管道近触地点处等效应力最大，顺向、侧向及逆向流时的最大值分别为180.7、206和 317 MPa。说明来流方向对管道等效应力影响较大，逆向流比顺向流的高出136.3 MPa，使得逆向流有使触地点曲率增大的趋势，工程实际中应尽量避免逆流作业。总之，采用θ=80°进行弃置回收作业，考虑波流影响的管道整体应力水平在许用应力范围内，作业安全有较好保障。

4 结论

(1)采用Pasternak地基模型和大挠度梁理论建立管道触底段和悬跨段的微分控制方程，利用ABAQUS软件可较好地处理管道的复杂受力和边界条件。

(2)提升角增大，管线提升端的轴向拉力减小、最大应力从提升点向触地点转移。当提升角处于合理范围时，管道应力水平较低，提升端轴向力相对于A＆R绞车能力比较合理。SSTB主管道和MEG管道提升角的合理范围分别是85°～60°和86°～40°。

(3)顺流时轴向拉力最大，A＆R绞车负载较大;逆流时管道轴向拉力最小。管线等效应力主要取决于弯曲应力。来流方向对管道触地点等效应力的影响非常大，逆流比顺流时高136.3 MPa，因此应避免逆流环境作业。

［1］龚顺风，何勇，周俊，等.深水海底管道S型铺设参数敏感性分析［J］.海洋工程，2009，27(4):87-95.

GONG Shun-feng，HE Yong，ZHOU Jun，et al.Parameter sensitivity analysis of S-lay technique for deepwater submarine pipeline ［J］.The Ocean Engineering，2009，27(4):87-95.

［2］曾晓辉，柳春图，邢静忠.海底管道铺设的力学分析［J］.力学与实践，2002，24(2):19-21.

ZENG Xiao-hui，LIU Chun-tu，XING Jing-zhong.Mechanical analysis of pipe laying ［J］.Mechanics and Practice，2002，24(2):19-21.

［3］甄国强，胡宗武.铺设过程中海底管道的非线性分析［J］.海洋工程，1993，11(3):28-38.

ZHEN Guo-qiang，HU Zong-wu.Nonlinear analysis of marine pipelines during laying ［J］.The Ocean Engineering，1993，11(3):28-38.

［4］DATTA T K.Abandonment and recovery solution of submarine pipelines［J］.Applied Ocean Research，1982，4(4):247-252.

［5］宋甲宗，戴英杰.海洋管道铺设时的二维静力分析［J］.大连理工大学学报，1999，39(1):91-94.

SONG Jia-zong，DAI Ying-jie.2D static analysis of submarine pipelines during pipelaying［J］.Journal of Dalian U-niversity of Technology，1999，39(1):91-94.

［6］KIMURA T，IDOGAKI S，TAKADA K，et al.Experimental and analytical studies of the elastoplastic behavior of offshore pipelines during laying［R］.OTC 3737，1980.

［7］詹侃，陆仁华.海底管道在铺设过程中的二维静态分析［J］.海洋工程，1991，9(4):14-20.

ZHAN Kan，LU Ren-hua.The 2-D statical problem of submarine pipelines during laying［J］.The Ocean Engineering，1991，9(4):14-20.

［8］PLUNKET R.Static bending stresses in catenaries and drill strings［J］.Journal of Engineering for Industry，1967，89(1):31-36.

［9］BREWER W J，DIXON D A.Influence of lay barge motion on a deepwater pipe line laid under tension［J］.Journal of Engineering for Industry，1970，92(3):595-604.

［10］POWERS J T，FINN L D.Stress analysis of offshore pipelines during installation［R］.OTC 1071，1969.

［11］帅健，吕英民，张进国.用动坐标迭代法分析海洋管道敷设时的应力［J］.油气储运，1996，15(10):21-24.

SHUAI Jian，LÜ Ying-min，ZHANG Jin-guo.Stress analysis of offshore pipelaying using the method of iteration in moving coordinate［J］.OGST，1996，15(10):21-24.

［12］ DNV.RP-F105.Freespanning pipelines［S］.Oslo:Det-Norske Veritas，2006.

［13］ DNV.OS-F101.Submarine pipeline systems［S］.Oslo:Det Norske Veritas，2007.

［14］ANDREUZZI F，MAIER G.Simplified analysis and design of abandonment and recovery of offshore pipelines［J］.Ocean Management，1981，7(1/4):211-230.

［15］PALMER A.Pipe laying in deep waters［J］.Journal of Offshore Technology，1994，2(1):13-17.

［16］刘延鑫，王旱祥，王 苗.海底管道局部冲刷数值模拟分析［J］.中国石油大学学报:自然科学版，2012，36(6):118-122.

LIU Yan-xin，WANG Han-xiang，WANG Miao.Numerical simulation analysis of local scour around submarine pipeline.［J］.Journal of China University of Petroleum(Edition of Natural Science)，2012，36(6):118-122.