航空发动机叶盘结构应力和变形的概率分析

白 斌，白广忱，童晓晨，李晓颖

（1.北京航空航天大学能源与动力工程学院，北京 100191；2.国家知识产权局专利局专利审查协作北京中心，北京 100081；3.河北联合大学电气工程学院，河北唐山 063009）

0 引言

航空发动机是飞机的心脏，是在高温、高压、高转速及严酷载荷工况下工作的复杂旋转机械装备，除了受到机械载荷和离心力等的影响外，燃气温度也是重要影响因素。在发动机总故障中，叶盘结构故障约占25%，严重影响发动机的安全性、可靠性、稳健性和效率等性能及对其失谐结构识别和预测[1-14]，如Kenyon在所建立的模型中分析了2个相间裂纹叶片对叶盘结构振动特性的影响规律（王艾伦等也做了类似研究），又采用谐波扰动法建立剪切弹簧环模型，研究了在微小失谐情况下受迫响应的灵敏度，采用灵敏度系数法对实际叶盘结构有限元模型进行优化；Bladh基于综合模态分析法（CMS）提出减缩模型（ROM），计算了受迫响应的概率问题，与MonteCarlo模拟方法相比，计算效率大大提高，之后又提出2次模态缩减模型（SMART），计算效率进一步提高，但是由于经过2次模态缩减使得计算精度严重降低。以上虽然对叶盘结构进行了不同程度的研究，但是都仅针对叶盘结构的机械力（如谐波周期激振力、气动力等作用下的振动情况）进行，并没有进一步对模型进行概率分析。航空发动机叶盘结构是转子结构，在高转速状态下，离心力的影响是不能忽略的，而且会产生陀螺效应，出现窝动现象，但该方面研究很少，而且没有考虑温度载荷这个非常重要的因素。Soize虽然考虑了离心力的影响，但建立的是非参数概率模型理论模型；Rossi等通过试验采用基本失谐模型识别方法对单族叶盘结构进行了响应的均值和方差等随机失谐概率统计特性研究；王建军等主要对刚度随机失谐叶盘结构模态特性进行概率分析。上述虽然对叶盘结构进行了大量概率统计特性研究，但多数采用MC法，比较耗费时间，而在航空发动机叶盘实际工作中受到多个复杂因素的共同作用，随着工作状态的不同而变化，因此需综合考虑各影响因素的随机性，进行概率分析。

基于以上研究的不足，本文考虑输入变量的随机性和不确定性，对叶盘结构的应力分布和叶盘结构的变形进行了概率分析。提出了1种极值响应面法（ERSM），能在不降低计算精度前提下显著提高计算效率，使得建立高保真实际叶盘结构有限元模型成为可能。在分析中考虑了温度载荷的动态性、离心力、Coriolis Forces和材料属性的随机性等，合理选取随机变量，利用有限元和极值响应面法相结合的思想进行动态概率分析。

1 极值响应面法基本理论

1.1 基本原理

首先，用MC法小批量抽取输入参数随机样本，对每个样本在分析时域[0,T]内求解系统动力学方程，得到其动态输出响应；然后将该动态输出响应在分析时域内的极值作为新的输出响应，称为极值输出响应，构造分析时域[0,T]内反映输入参数与极值输出之间关系的函数——极值响应函数，选取s组输入随机变量及对应的输出极值响应面数据，代入极值响应函数并确定其系数；最后利用极值响应面函数计算系统的可靠度。这种方法称为极值响应面法。而本文是对每个抽样样本在分析时域[0,T]内求解有限元模型，用该响应函数代替有限元模型计算系统的动态极值输出响应。该方法不计算系统每一时刻的输出响应，只计算分析时域[0,T]内不同输入随机变量对应的输出响应极值，然后用MC法进行抽样，将抽样数据代入极值响应函数，代替有限元模型计算系统的动态极值输出响应，从而进行系统的概率分析，其计算流程如图1所示。

图1 有限元极值响应面法动态概率分析流程

1.2 数学模型

写成响应面函数形式

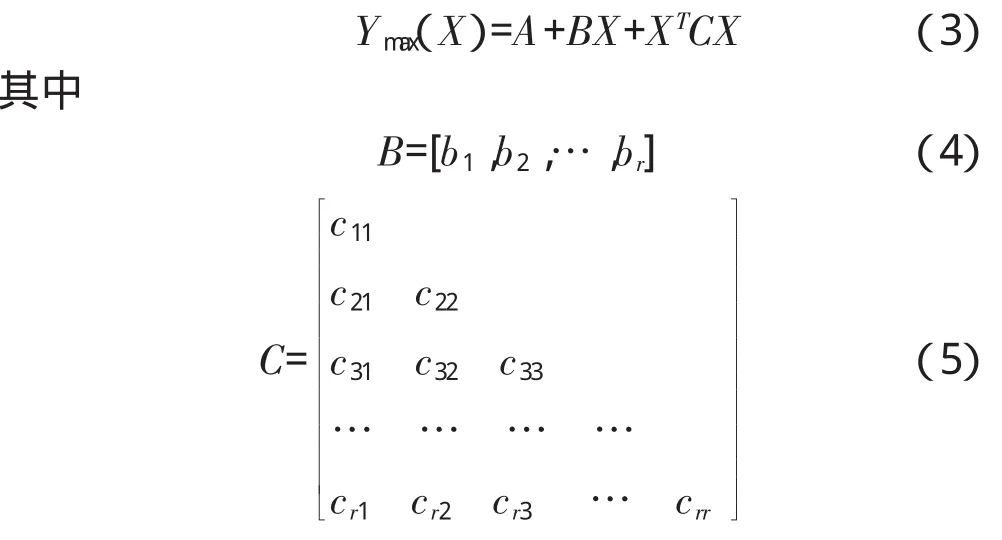
式中：j=1,2,3，…，M，M为样本点数；r为输入变量数。

式（2）或式（3）称为极值响应面函数，由该函数确定的输入输出关系曲线（或曲面）称为极值响应曲线（或极值响应曲面），在求解极值响应面函数系数时，在极值输出响应中选取足够数量的试验点，将试验点的数据代入式（2）或式（3）中，确定极值响应面函数的系数A、B、C，得到极值响应面函数的表达式。然后用该极值响应面函数代替有限元模型进行相应概率分析。

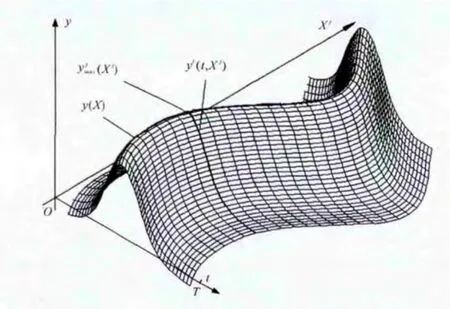
图2 有限元-极值响应面法原理

2 概率分析方法

2.1 可靠度计算

概率分析用于评估模型的输入参数或假设条件对输出结果的影响，进而确定结果的分布情况，以避免了过设计，可以对零部件在工况下的可靠性给出定量结果，以保证其安全性。在确定响应面函数（R S F）后，若系统真实输出为Y（X），则系统的极限状态函数为

所以系统极限状态函数g（X）的均值和方差为

由于各随机变量相互独立，则极限状态函数g（X）服从高斯分布，可靠性指标和可靠度分别为

式中：Φ（·）为标准正态分布。

2.2 灵敏度分析

可靠性灵敏度一般定义为失效概率对基本变量分布参数的偏导数。令失效概率为PF，所以

则失效概率的灵敏度为

上文所获取的可靠性灵敏度估计值只是近似的，在样本容量很小时可靠性灵敏度估计值有很大随机性，但依据大数定理，式（1 5）或式（1 6）的估计值随样本容量的增加逐渐趋于真值。为了更加清楚地了解可靠性灵敏度的收敛性和精度，需要对式（1 5）或式（1 6）中所列的数学期望和方差进行分析，又因为各样本之间相互独立，所以可以以样本均值和方差代替总体的数学期望和方差，则

3 航空发动机叶盘结构热传递分析

航空发动机涡轮叶盘的结构变形除了受离心载荷、机械载荷和气动力载荷等作用外，燃气温度的影响也不能忽略，主要从热传导和换热和热边界条件等对其进行分析[15-16]。

3.1 导热微分方程

在圆柱坐标系下，航空发动机叶盘结构在温度场内，根据傅里叶定律建立3维导热微分方程

式中：r、φ、z为航空发动机叶盘结构在温度场中点的坐标；ρ、c分别为结构材料的密度和比热；kr、kφ、kz为结构材料的导热系数。

3.2 热传导分析

航空发动机叶盘结构内部存在温度差，即存在温度梯度，热量从叶盘的高温部分传到低温部分且叶盘与传动轴等相互接触，热量也会从高温部件传到低温部件，因此满足热传导方程，即

式中：Q为时间t内的传热量或者热流量；K为热传导系数；Thot、Tcold分别为叶盘高、低温部分（或者高、低温部件）温度；d为叶盘厚度；A为叶盘侧面积。

3.3 热对流分析

由于温差导致航空发动机叶盘结构表面和与其接触的气流之间存在热量的交换，因而航空发动机叶盘结构表面发生对流现象，用牛顿冷却方程描述为

式中：α为对流换热系数；TS为叶盘表面温度；TB为周围气流温度；Re为雷诺数；ω为轮盘旋转角速度；r为计算半径，即计算区域的平均半径；v为冷却空气动黏性系数；Va为冷却空气的轴向速度；V0为计算半径处的圆周速度。

3.4 热边界条件

为使每个节点的热平衡方程具有惟一解，必须附加热边界条件和初始条件。航空发动机计算的边界条件有3类。

（1）给定物体边界上的温度，即给定叶盘表面温度分布情况

式中：Γ为物体边界；f（.）为已知温度函数。

（2）给定物体边界上的热流，即叶盘边界上通过叶盘表面的热流密度为已知

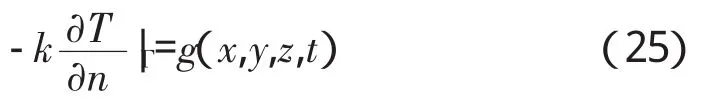
（3）给定物体边界上的换热系数和环境温度，通常也称为对流换热边界条件，这是在叶盘的边界上与外部介质之间进行的对流换热过程，边界上的热交换条件为

式中：h为叶盘边界与周围气流之间的换热系数；Tf为周围流体的温度；Tw为结构体边界表面温度；Tf为周围流体的温度。

3.5 初始条件

初始条件表示为

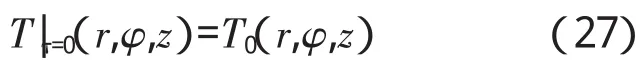
式中：T0为结构体初始温度。

对于叶盘结构的某些部位（如轮盘的外缘、中心或轮毂内径）的温度通常可以在技术文件中找到或者用试验方法确定，所以可以当作第1类边界条件处理。在一般情况下轮盘传给主轴的热量很小，可忽略不计，因此可以将轮盘与主轴的连接处考虑为绝热边界，由于边界上无热量传递，热流密度为零，可以视作第2类边界条件的特殊情况。对于轮盘侧表面和叶片，若已知气流的压力、温度、流量等，则可根据传热学公式分别计算出其放热系数，作为第3类边界条件处理。

4 航空发动机叶盘结构确定性分析

4.1 载荷谱计算

为了更符合实际，选取发动机从地面起动—慢车—起飞—爬升—巡航作为计算范围，取12个关键点作为计算点[17]，计算载荷谱如图3所示。考虑动态温度的影响、叶盘材料的非线性、导热系数和非线性膨胀系数、比热、对流换热以及离心力、陀螺效应等影响，对其进行动态热与结构耦合分析。

图3 载荷谱随时间变化图谱

4.2 叶盘结构有限元模型

选取某型发动机第2级高压涡轮叶盘作为研究对象，简化其叶片的冷却孔、轮盘的倒圆角和凸台等，材料选为某镍合金，则有限元模型如图4所示。本文在研究中假设叶盘结构为理想的周期对称结构，且不考虑加工误差等，选取1个扇区作为研究对象，其有限元模型如图5所示。

图4 整体有限元模型

图5 单扇区有限元模型

4.3 叶盘结构确定性分析

根据如图3所示的载荷谱，对图5的扇区叶盘结构进行瞬态动力计算分析，得到其在离心载荷、温度载荷和Coriolis Forces共同作用下的变形随时间的变化规律，如图6所示。

图6 叶盘结构变形随时间的变化曲线

研究结果表明，在飞机爬升过程中转速和燃气温度基本达到最大值时叶盘结构总变形和应力集中均达到最大值，且在切向的变形大于径向和轴向的变形，应力主要集中于叶片根部，而总变形发生在叶尖处，实际上产生该效果的主要原因是离心力、温度和Coriolis Forces共同作用的结果，与实际相符合。取最危险节点作为研究对象，此时叶盘结构的应力分布和总变形如图7、8所示。

图7 叶盘结构应力分布

图8 叶盘结构总变形

5 叶盘结构变形的动态概率分析

5.1 随机变量的选取

航空发动机叶盘在加工和实际使用中其材料参数和工作条件都存在不确定性，在动态概率分析时随机变量的选取较稳态时的概率分析复杂，基于有限元的概率分析为参数化建模分析，参数的选取非常重要，在此采用最值选取法，其选取过程如下：

（1）选取输入变量X中某个变量Xi中元素的最大值，记作ximax，Xi中所有元素均除以ximax，即

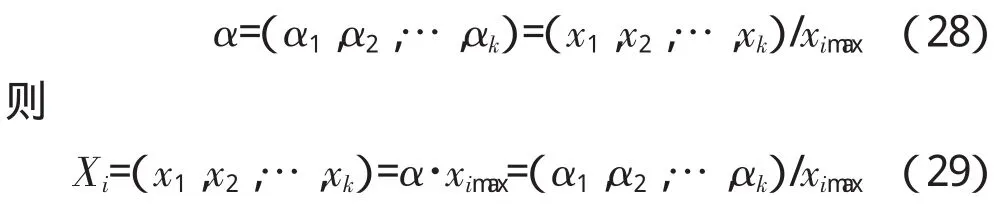
（2）将输入变量X中的所有变量，即X=（X1，X2，…，Xr）中每个变量中元素的最大值形成数组集合X˜={x1max,x2max,…，xrmax}，若用Y表示X˜，即Y=（y1,y2,…，yr），则X与Y各元素间仍存在对应关系，即

（3）用ximax代替Xi中各元素来分析对输出响应的影响，再根据Xi中各元素与ximax间的相关性确定Xi中各元素对系统输出的影响。

该方法只需考虑1类变量的最大值对输出响应的影响，大大减少了随机输入变量数，为动态概率分析提供了方便，能大大节约计算时间和提高计算效率与精度。

根据该方法选取航空发动机叶盘结构的随机输入变量，包括叶盘转速ω、燃气温度t、膨胀系数al、导热系数λ、对流换热系数h、比热容c、材料密度ρ、弹性模量E、泊松比ν，假设各变量均服从高斯分布且相互独立，见表1。

表1 叶盘结构随机输入变量及其数字特征

5.2 动态概率分析

首先建立叶盘结构的应力分布和总变形与随机输入变量的极限状态方程（式（31）、(32)），同时可以得到应力分布和总变形与任意2个输入变量之间的极值响应面的关系，如图9、10所示，再利用该极限状态方程进行叶盘结构总变形和应力的概率及灵敏度分析。

图9 应力极值响应面

图10 总变形极值响应面

极值响应面函数代替叶盘结构的有限元模型，利用Box-behnken矩阵抽样法得到147组样本点，则应力分布和总变形样本分布如图11、12所示。利用MC法进行1万次抽样，得到其模拟样本历史如图13、14所示，累积分布函数如图15、16所示，样本直方图如图17、18所示。同时进行逆概率分析，其结果见表2。根据表1提供的参数，当置信区间为0.95，叶盘结构应力分布和总变形均服从正态分布，且均值和标准差分别为979.24MPa、3.452mm，4.464MPa、0.242mm，可靠度R≈98.99%。

5.3 灵敏度分析

图11 应力样本分布

图12 总变形样本分布

图14 总变形模拟样本

图15 应力累积分布函数

图16 总变形累积分布函数

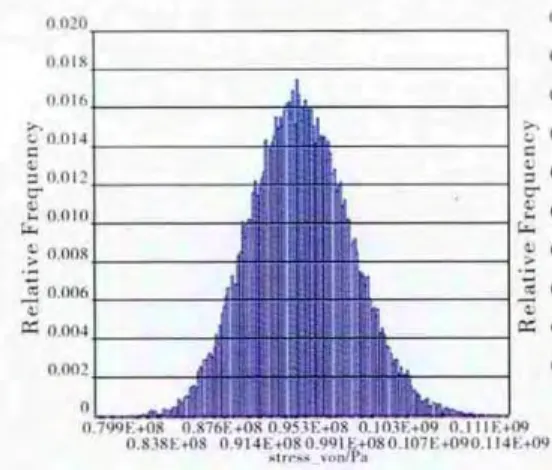
图17 应力样本

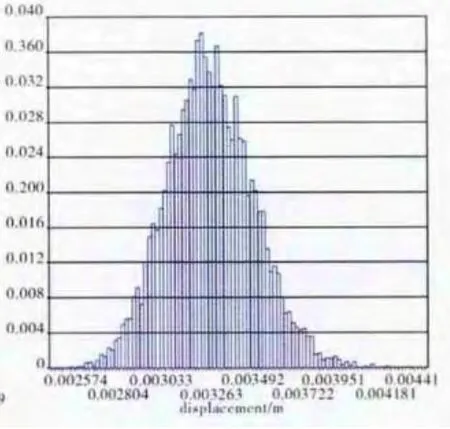
图18 总变形样本

表2 不同可靠度（部分）下变量的极限值

灵敏度即指分析随机输入变量的变化对输出参量稳定性的影响程度，进而决定哪些参数对可靠性失效影响较大。从式（14）～（19）中可得各随机变量的灵敏度及其对叶盘的影响概率和应力与总变形之间的相关性，如图19～21所示，并见表3。

从图20、21和表3中可见，转速和燃气温度是影响叶盘结构应力分布的最主要因素，其影响概率分别为27.40%、25.05%，而对于总变形，转速对其影响最为明显，影响概率为43.05%，其次为弹性模量和密度，在各变量的影响中有正负之分，正表示该变量与应力或者总变形为正相关，而负则说明该变量可能有抑制应力或者变形增大的作用，可见比热容增大可能会抑制应力的增大，而弹性模量的增大会抑制变形的增大，因此需要综合考虑各因数，采取适当措施来抑制应力和变形的增大。

图19 总变形和应力分布相关性图谱

图20 应力场灵敏度

图21 总变形灵敏度

表3 叶盘结构随机输入变量的灵敏度和影响概率

5.4 有效性验证

为验证ERSM的效率和精度，基于表1中的随机输入变量和统计特征及相同计算环境条件下，分别与MC法和RSM对叶盘结构的变形进行动态概率分析，并比较计算结果。在计算过程中，3种方法都是1万次模拟计算，其中ERSM和RSM的抽样次数均为147，以MC法计算为基准，其对比结果见表4。

表4 3种方法概率分析结果比较

从表4中可见，与MC法相比，本文提出的极值响应面法的计算精度和效率均高，但计算时间仅为MC法的1/68、传统响应面法的1/3。可见，FE-ESRM既能保证计算精度，又可大大缩短计算时间和提高计算效率。

6 结论

（1）介绍了动态概率分析的极值响应面方法并且建立了数学模型，同时给出了可靠性计算和灵敏度分析方法。

（2）以某型发动机从地面起动—慢车—起飞—爬升—巡航过程作为计算范围，考虑温度载荷、离心力和Coriolis Forces的耦合作用，建立了航空发动机整体叶盘结构限元模型，以单扇区为研究对象进行确定性分析并且计算了输出响应随时间的变化规律，找出了变形和应力达到最大值时的节点并分析了此时的应力和变形的变化规律。

（3）考虑了热载荷和转速的动态性及随机性，以及材料的非线性等因素的影响，采用极值响应面法对叶盘结构的输出响应和应力分布进行了概率分析，获得了叶盘结构的应力和总体变形的极值响应面，以及样本分布、模拟样本、历史直方图、累计分布函数的变化规律。

[1] Kenyon J A, Griffin J H. Forced response of turbine engine bladed disks and sensitivity to harmonic mistuning [J]. Journal of Engineering for Gas Turbines and Power, 2003,125（1）:113-120.

[2] Kenyon J A, Griffin J H, Kim N E. Sensitivity of tuned bladed disk response to frequency veering [J]. Journal of Engineering for Gas Turbines and Power, 2005,127（4）:835-842.

[3]王艾伦,黄飞.裂纹叶片分布对失谐叶盘结构振动特性的影响[J].振动与冲击,2011,30（4）:26-28,9.

WANG Ailun, HUANG Fei. Effect of cracked blade distribution on vibration characteristics of a mistuned bladed disk [J].Journal of Vibration and Shock, 2011,30（4）:26-28,9. (in Chinese)

[4] Petrov E P. A method for forced response analysis of mistuned bladed disks with aerodynamic effects included [J]. Journal of Engineering for Gas Turbines and Power, 2010,132（6）: 1-10.

[5] Judge J, Pierre C, Mehmed O. Experimental investigation of mode localization and forced response amplitude magnification for a mistuned bladed disk [J]. Journal of Engineering for Gas Turbines and Power ,2001,123:940-950.

[6] Bladh R, Pierre C, Castanier M P, et al. Dynamic response predictions for a mistuned industrial turbomachinery rotor using reduced order modeling [J]. Journal of Engineering for Gas Turbines and Power,2002,124（2）:311-324.

[7] Soize C, Lombard J P, Dupont C, et al. Blade manufacturing tolerances definition for a mistuned industrial bladed disk [J].Journal of Engineering for Gas Turbines and Power, 2005, 127（3）:621-628.

[8] Rossi M R, Feiner D M, Griffin J H. Experimental study of the fundamental mistuning model for probabilistic analysis [C]// A Proceedings of the ASME Turbo Expo. Reno-Tahoe: American Society of Mechanical Engineers ,2005:373-380.

[9]王建军,姚建尧,李其汉.刚度随机失谐叶盘结构概率模态特性分析[J].航空动力学报,2008,23（2）:256-262.

WANG Jianjun, YAO Jianyao, LI Qihan. Probability characteristics for vibratory mode of bladed disk assemblies with random stiffness mistuning [J]. Journal of Aerospace Power,2008,23（2）:256-262. (in Chinese)

[10] Sinha A. Computation of the statistics of forced response of a mistuned bladed disk assembly via polynomial chaos [J].Journal of Vibration and Acoustics, 2006,128（3）:449-457.

[11] Mbaye M, Soize C, Ousty J P, et al. Robust analysis of design in vibration of turbomachines[J]. Journal of Turbo-machinery,2013,135（2）: 1-8.

[12] Mayorca M A, Vogt D M, Fransson T H. A new reduced order modeling for stability and forced response analysis of aero-coupled blades considering various mode families [J].Journal of Turbomachinery,2012,134（5）: 1- 10.

[13] Holland D E, Epureanu B I, Filippi S. Structural damping identification for mistuned bladed disks and blisks [J]. Journal of Vibration and Acoustics, 2012,134（2）: 1-3.

[14] HE Erming, WANG Hongjian. A multi-harmonic method for studying effects of mistuning on resonant features of bladed disks with dry friction damping [J]. Chinese Journal of Aero nautics,2006, 19（4）:321-325.

[15]李朝阳,张艳春.燃机涡轮盘三维瞬态温度及应力场计算分析[J].动力工程,2006,26（2）:211-214.

LI Chaoyang, ZHANG Yanchun. Calculation and analysis of the transient 3-dimensional temperature and stress field of a gas turbine’s disk[J]. Journal of Power Engineering, 2006, 26 （2）:211-214. (in Chinese)

[16]关磊,汪家道,陈大融.微小型发动机气缸温度场及热变形的三维有限元分析[J].清华大学学报(自然科学版),2003,43（11）:1487-1490.

GUAN Lei, WANG Jiadao, CHEN Darong. 3-D finite element analysis of microengine cylinder temperature field and heat deformation [J]. Journal of Tsinghua University (Science and Technology) ,2003, 43（11）:1487-1490. (in Chinese)

[17]费成巍,付黎,柏树生,等.高压涡轮叶尖径向运动间隙非线性动态分析[J].航空发动机,2013,39（1）:38-42.

FEI Chengwei, FU Li, BAI Shusheng, et al. Nonlinear and dynamic analysis of HPT blade-tip radial running clearance [J]. Aeroengine, 2013,39（1）:38-42.(in Chinese)