关于幂定律风切变公式的应用研究
2014-04-26苏志勇尤扬
苏志勇,尤扬
(1.北车风电有限公司,济南 250022;2.WindSim China,北京 100029)
0 引言
在风电场工程的前期阶段,当测塔实测数据不含拟选机组轮毂高度处数据时,要通过风切变公式将实测数据推导至轮毂高度。目前工程常用方法是采用测塔最高的一层和其下最近的一层数据来计算,该方法存在一定缺限,本文从理论分析入手,提出一种改进计算的方法。
1 理论分析
标准中风切变的公式如式(1)所示:

式中z1和v1作为基准高度和基准风速,在风切变指数α确定的情况下,可通过该公式计算任意高度的风速,但实际工程中α属未知量,要首先求出该值再计算其它高度层的风速。在实际工程中各测风高度的数值为已知量,通过数学计算即可得α值。
从理论上来说α是一个受天气系统影响不断变化的数值,同时其数值也与地形及地表粗糙度有直接关系,工程上假定大气层结为中性时得出上述公式,而采用两个高度数据的常用方法来求其它高度层风速时与实际往往有一定误差。
本文提出的方法与目前常用方法不同之处就是综合所有高度层数据通过最小二乘法进行拟合α值。考虑到风电场实际环境,测塔各个测风高度层均受到地表粗糙度及地形的影响,通过流体力学的理论分析可知,在流场中距流体边界越近的地方受边界外形影响越大,这样基准层宜取距地面最远的测风高度层,可尽量减少地表粗糙度及地形对测量数据的影响。新方法与常用方法对比如表1所示。
2 实际工程验证
考虑工程的代表性,作者选取包括山东、河北、内蒙古、黑龙江、吉林、辽宁、贵州、湖南等省及自治区的多个测塔数据进行处理,考虑到计算的对比性,从中选取具有4层测风数据的测塔数据20个测塔数据进行分析。各测塔数据如表2所示。
每个测塔将测塔第4层数据作为目标数据,分别用其它三个高度作为基准层拟合切变值,计算第4层数据,同时采用目前常用方法使用第二层数据和第三层数据来计算第4层数据,各测塔拟合相关性如表3所示。
将所有计算结果与实测数据的差值进行统计,绘制误差分布图如图1所示。
从图中可看出Pv3计算大部分误差分布要较常用方法得出的误差相对集中,且集中于1%附近,Pv2和Pv3较Pv1要差。
参考统计[2-3]的方法取各计算数值的误差均值与标准差计算90%置信度的误差如表4所示。

表1 两种方法对比
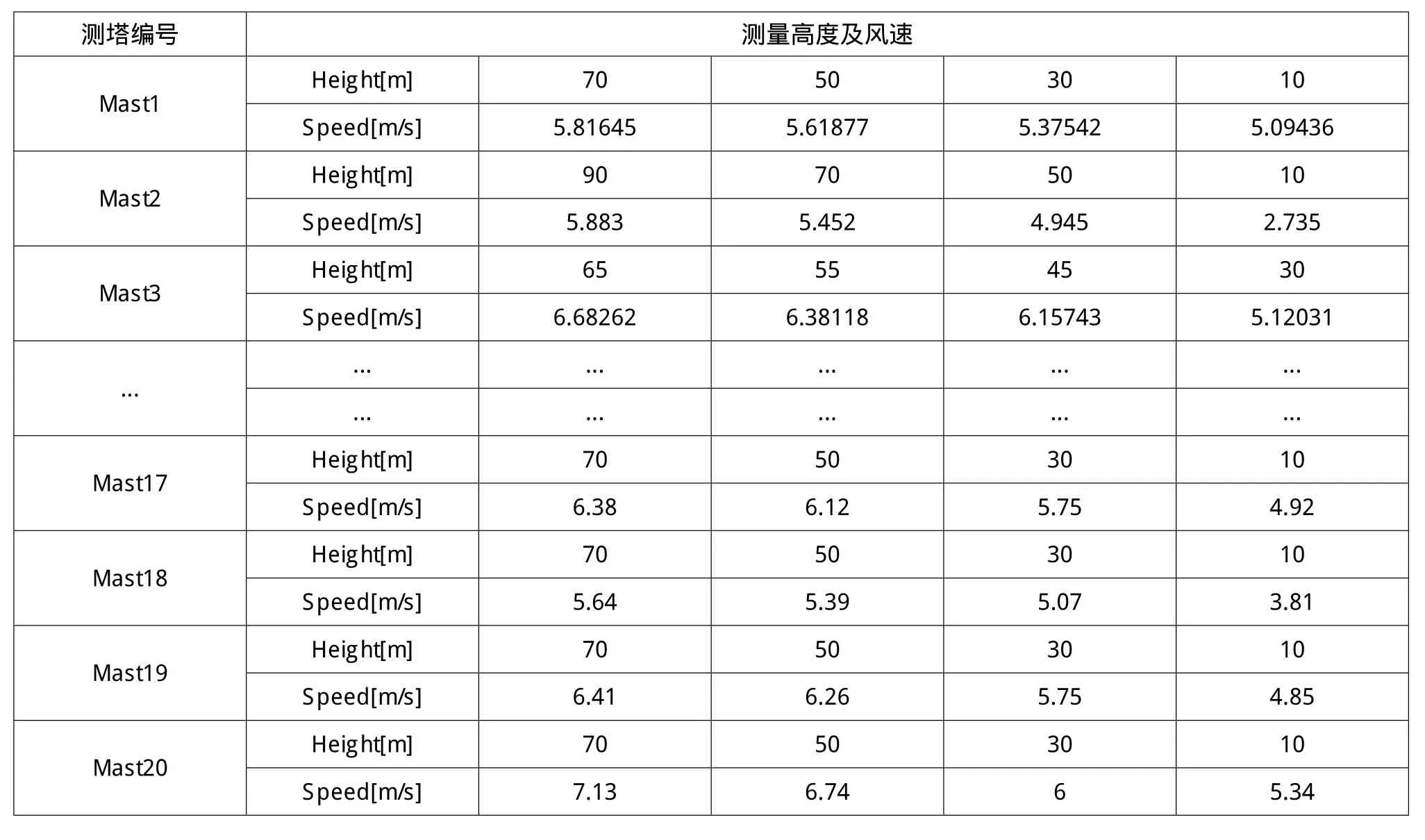
表2 测塔数据表
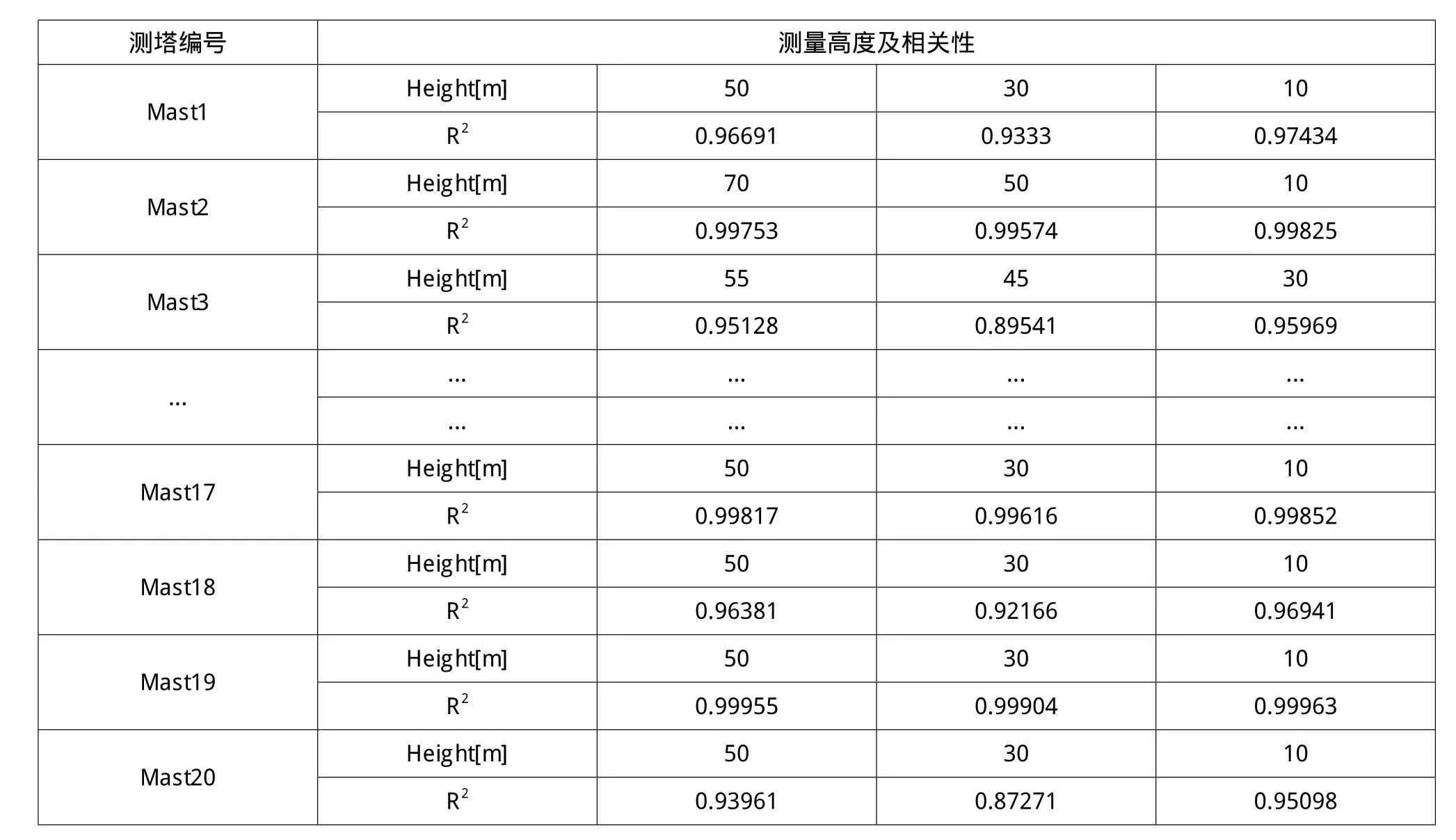
表3 拟合相关性

图1 误差分布图

表4 90%置信度误差表
通过表4可知,进行拟合计算时基准层宜选取距地面最远的高度层。对于统计结果中第二高度层误差最大的原因,经初步分析,可能是由于测塔周边植被对测塔处流场的影响,详细的分析则是下一步工作的重点。
3 结论
本文通过对审定律风切变公式的分析,提出使用全部测量高度层数据计算风切变指数的方法。通过对实际工程的对比可知,在实际使用该方法时,选取的基准层宜取距地面最远的测风高度层。以目前使用的测塔数据进行分析的结果看,新计算方法要总体结果要优于目前常用计算方法,在风电场工程前期工作中应用该方法,可提高工程计算的精度。

[1]施鹏飞,朱瑞兆.GB/T 18710-2002 风电场风能资源评估方法[S].北京:中国标准出版社,2002.
[2]IEC 61400-1.Wind turbines-Part 1:Design requirements,ThirdEdition[S].2005.
[3]John A.Rice ,Mathematical Statistics and Data Analysis, Third Edition [M].Berkeley, University of California,2007.
