伺服系统变增益速度控制策略研究

杨亮亮，熊琰，李叶松

（华中科技大学自动化学院，湖北武汉 430074）

1 引言

转矩扰动是影响伺服系统速度控制性能的主要因素。常见的扰动类型有瞬态常值负载扰动和周期性负载扰动两种，瞬态常值扰动的影响可以通过控制器快速调节消除；而对于周期性负载扰动的影响，则需要采用控制策略加以实时抑制。通常采用的扰动抑制方法有扰动观测器［1］补偿方法，该方法是一种闭环调节方法，可以有效抑制扰动的影响，但计算复杂，参数依赖性强，且设计缺乏明确的方法；高增益控制方法［2］是一种实现简单的设计方法，但要求系统有高速的电流环控制特性，因此参数设计上存在稳定性条件的限制。本文研究分析了一种新型速度伺服控制策略，在使用PI控制策略保证稳定性的前提下，利用变增益的方法动态改变控制器零点配置以加快系统对于扰动的调节作用，同时基于积分预测对控制器进行抗饱和处理，不仅可以改善系统稳态时的抗扰动特性，而且提高了系统的动态响应性能。

2 周期性扰动转矩及控制器特性分析

2.1 周期性扰动转矩（齿槽转矩为例）特性分析

在伺服电机运行时，除一般的负载扰动外，由于机械联接、承受变化负载以及电机内部结构等原因会产生周期性转矩扰动，这种扰动难以完全消除，会影响速度伺服控制的精度。这里以永磁同步电机内部齿槽转矩为例，分析其特性。

在永磁同步伺服电机内部，定子电枢铁心齿槽与转子永磁体之间产生相对运动时，永磁体两侧面跟与其对应的一至两个电枢齿槽之间的磁导变化较大，引起磁场储能变化，从而产生齿槽转矩。

若将整个圆弧面剖开为平面如图1所示，θ0为转子机械位移为零的位置，机械位移角为θ，坐标α为永磁体中心向两边延伸的气隙坐标。

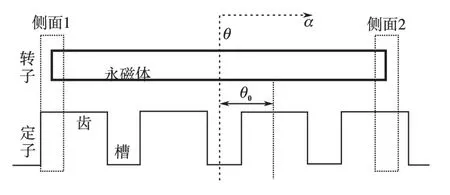
图1 永磁同步电机转子圆弧面的平面示意图Fig.1 Schematic plan view of the circular surface of PMSM rotor

使用能量法［3］推导齿槽转矩：

磁场能量：

利用傅里叶变换将式（2）展开并化简，带入式（1）中，可得：

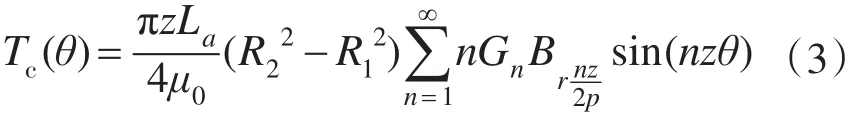
式中：R1为转子外半径；R2为定子内半径；La为电枢铁芯轴向长度；n为使zn/2p取整的整数。

从式（3）可以看出，齿槽转矩是转子位置角θ的函数，其频率与速度相关，另外频率还取决于极对数p和齿槽数z。这种周期性转矩扰动会引起速度的波动，是固有存在的，虽然通过槽极结构的设计可以减小，但是难以消除，对于高精度的速度伺服特性具有重要的影响，需要采取相应的控制措施加以抑制。

2.2 控制器特性分析

图2为速度控制环简化数学模型［3］（这里假设电流环具有足够快控制特性）。由于实际物理输出的限制，在控制器实现时必须对控制器输出进行限幅，因此会产生积分饱和现象［4］，影响PI控制性能。

速度传递函数Gω(s)与转矩传递函数GM(s)分别为

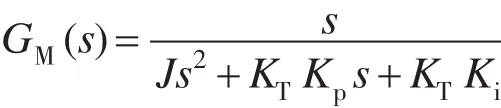
分析GM(s)的幅频特性可以看到，增大Kp，Ki都可以减小GM(s)幅频特性增益，抑制周期性负载扰动的影响。但是Kp增大会使速度传递函数Gω(s)的响应带宽显著加大，由于电流内环带宽的限制，会引起震荡，影响稳定性；Ki的变化不会显著增大Gω(s)的响应带宽，却能够有效减小GM(s)在低频段的幅频特性增益，因此采用变积分增益的方法可以在不影响伺服系统稳定性的基础上，使系统具有更宽泛的扰动抑制能力。

3 变增益及积分预测抗饱和速度控制策略

变增益速度控制结构框图如图3所示，通过变增益控制增强系统稳态时的抗扰动性，另外针对物理输出限幅，利用积分预测算法对控制器进行抗饱和处理，改善动态响应性能。

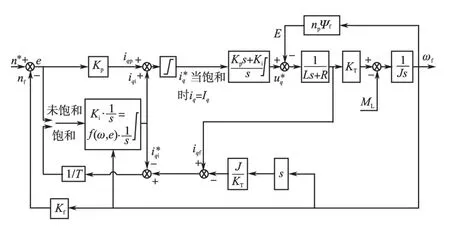
图3 控制策略结构框图Fig.3 Control strategy block diagram

3.1 变增益方法

通过对控制器特性分析可知，增大Kp，Ki能够有效提高系统的抗扰动性，提高伺服驱动系统的刚度。但Kp增大会显著加大速度控制环的响应带宽，由于实际物理限制，过大的Kp会引起系统震荡。图4为改变Ki时Gω(s)的幅频特性曲线，可以看到增大Ki能够有效减小低频周期扰动到速度输出的幅值增益。如果单独增大Ki，虽然增强了系统的抗扰动性，但Kp，Ki不能够协调配合，

图2 速度控制环的简化数学模型

Fig.2 Simplified mathematical model of the speed control loop可能会增大响应的超调量，影响瞬态运行性能。因此采用变积分增益的方法，动态配置控制器零点，以同时满足动态和稳态要求。

由下式可知|GM(jω)|是一个先递增后递减的函数，在频率ω=处取得最大值。

图4 Gω(s)幅频特性曲线Fig.4 Amplitude-frequency characteristic curves ofGω(s)

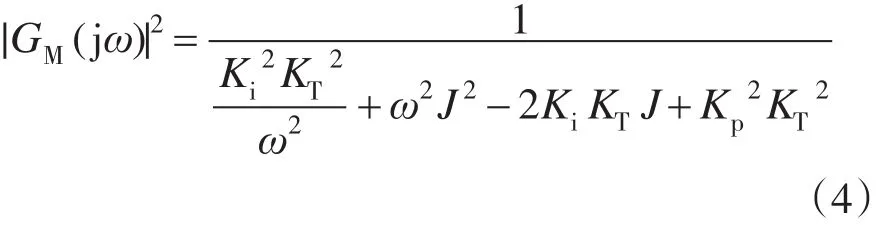
令KI为系统稳态时的积分增益、ki为满足动态响应性能的积分增益。若KI=Kω，则可以保证稳态时|GM(jω)|2≤1（/K2-2KiKTJ+），K根据扰动幅值与控制精度的要求适当取值，K越大则扰动抑制效果越好，但过大会导致系统不稳定。为简化计算，KI的取值根据频率分为2个阶段，当ω＜时，KI=Kω；当ω≥时，KI=保持不变。

变增益过程通过函数f实现，f要求系统接近稳态时，Ki的值能够迅速从ki增大到KI，这里通过误差绝对值|e|的倒数来实现变增益过程。周期性负载扰动的频率一般与转速成正比，以齿槽转矩为例，稳态转速恒定时θ=ωft，ωf为机械角速度，将其带入式（3）可知，扰动转矩的频率为nzωf。变增益函数为f（ωf，e），整个变增益过程函数表示如下：

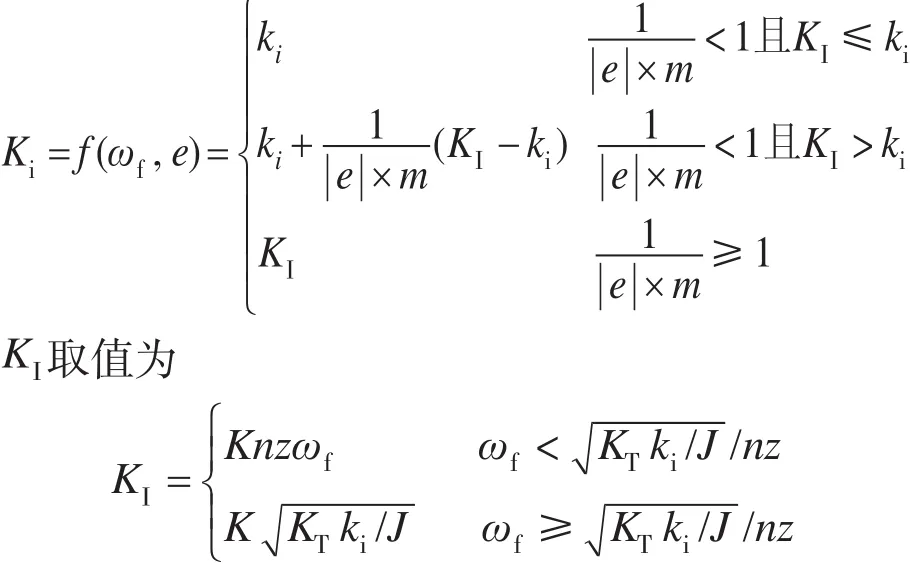
其中，Ki为在线性定常条件下设计的满足动态性能的积分增益；m用来调整Ki增大的数值范围；K的取值与周期性扰动幅值、速度控制精度要求、电机齿槽数以及极对数有关，在满足稳定性的前提下，K越大越能够增强系统稳态时的抗扰动性能。

3.2 基于积分预测的抗饱和处理

PI控制器参数是在线性区整定的，传统方法忽略饱和现象引起的非线性因素，控制性能比期望的差［5］。针对饱和问题，文献中有很多改进方法，例如采用智能PI控制限制积分器的作用［6］，或者采用反向计算抑制抗饱和［7］等，这些方法有的效果不理想，有的计算复杂，缺乏合理性。

本文利用积分预测进行抗饱和处理，在PI控制器处于饱和期间，使用积分项对负载力矩进行预测，代替对速度误差的积分，达到抗饱和的目的。

对于恒转矩负载，进入稳态后，控制器输出等于积分值。在控制器饱和阶段，指令力矩电流恒定，控制对象近似匀加速。预测的目的就是控制器退饱和时，积分值即为稳态时控制器的输出值。

控制器饱和状态下，iq=±Iqmax=Iq；稳定状态下，iq=，其中=ML/KT；实现对的预测，关键在于转动惯量J和转矩常数KT的估计，可通过离线或在线方式获得。

饱和状态：

稳定状态

将式（5）带入式（6）：

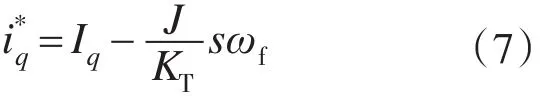
PI控制器由比例计算结果iqp和积分计算结果iqi两部分组成，控制器调节过程分为饱和、未饱和两种状态：未饱和时，iqp=Kpe，iqi=Kie(1/s)；饱和状态时，为实现iqi动态跟踪，利用积分作用，将其设计成闭环结构，iqi=(Ki/T)(1/s)(-iqi)，成为一阶惯性环节iqi=[1/(Ts/Ki+1)]，（见图3）。

前面推导中认为控制器饱和时电机近似匀加速，实际调节过程中，由于速度的变化使得反电动势动态变动，实际转矩电流不等于指令电流值，预测计算中用q轴电流反馈值iqf代替指令电流Iq，实现准确预测。

4 实验结果

实验在基于ARM Cortex M4的交流伺服驱动平台上完成。采用的永磁同步伺服电机参数为：Mo=6 N·m，Mn=4.5 N·m，nN=1 200 r/min，Io=5.5 A，nmax=2 000 r/min，J=17.6×10-4kg·m2，磁极对数为3。

图5所示为电机在相同PI参数，不同转速下，稳态时速度的频谱分析，可以看出，齿槽转矩引起的波动频率与转速成正比，幅值变化规律与前述分析相同。

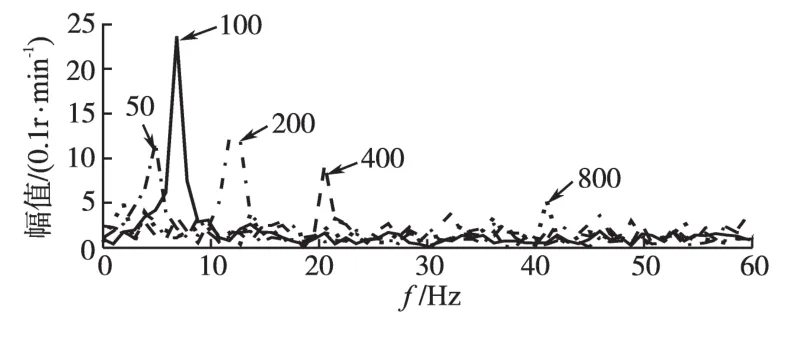
图5 稳态下不同转速频谱分析Fig.5 Spectrum analysis of the different speed in steady state

图6、图7分别为采用PI控制与变增益PI控制的速度响应结果，通过对比看出，在满足动态响应要求的情况下，进入稳态后，采用PI控制时速度会有较大波动，而采用积分变增益预测PI控制，波动能够得到很好的抑制。

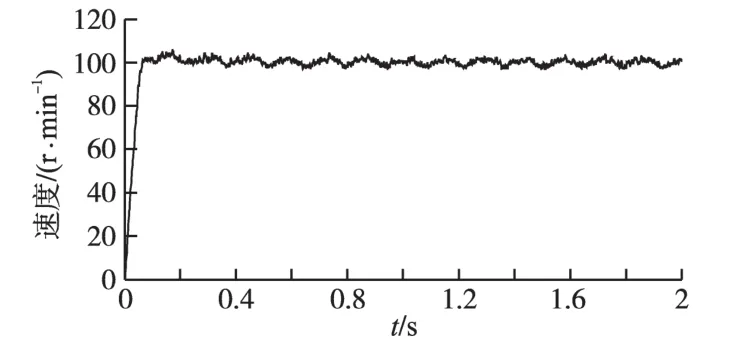
图6 传统PI控制速度响应曲线图Fig.6 Traditional PI control speed response curve

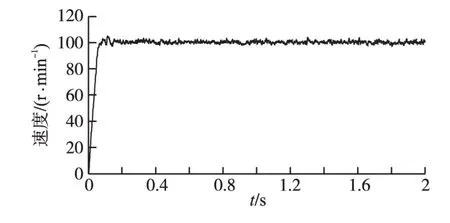
图7 变增益PI控制速度响应曲线Fig.7 Variable gain PI control speed response curve

图8、图9分别为给定速度1 200 r/min时，采用积分预测抗饱和处理的速度和q轴电流响应曲线，可以看出利用积分预测具有较好抗饱和效果。

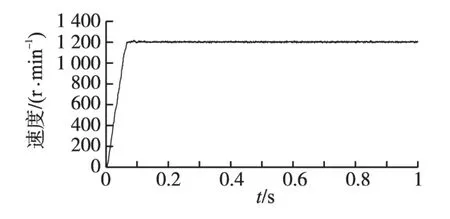
图8 1 200 r/min速度响应曲线Fig.8 1 200 r/min speed response curve

图9 1 200 r/minq轴电流响应曲线Fig.9 1 200 r/min q-axis current response curve

5 结论

本文对交流伺服系统应用中的周期性负载扰动以及伺服控制特性进行了深入分析，提出一种变积分增益速度控制策略增强系统抗扰动性的方法，通过动态配置控制器零点，在保证系统稳定以及较好瞬态响应性能的前提下，抑制周期性负载扰动的影响，提高稳态时速度控制精度，通过对控制器进行积分预测抗饱和处理，减小系统超调量，提高动态响应性能。实验结果表明，整个速度控制策略简单、有效。

［1］ Lee Kyo-Beum，Blaabjerg F.Robust and Stable Disturbance Observer of Servo System for Low-speed Operation［J］.IEEE Transactions on Industry Applications，2007，43（3）：625-635.

［2］ 秦忆，周永鹏，邓忠华，等.现代交流伺服系统［M］.武汉：华中理工大学出版社，1995.

［3］ 王秀和.永磁电机［M］.北京：中国电力出版社，2007.

［4］ 陈伯时.电力拖动自动控制系统［M］.第3版.北京：机械工业出版社，2003.

［5］ Zhang Da，Li Hui，Emmanuel G Collin.Digital Anti-windup PI Controller for Variable Speed Motor Drives Using FPGA and Stochastic Theory［J］.IEEE Transactions on Power Electronics，2006，21（5）：1496-1501.

［6］ 刘金琨.先进PID控制Matlab仿真［M］.北京：电子工业出版社，2004.

［7］ Ohishi K，Hayasaka E，Nagano T，et al.High-performance Speed Servo System Considering Voltage Saturation of a Vector Controlled Induction Motor［J］.IEEE Transactions on Industrial Electronics，2006，53（3）：795-802.

修改稿日期：2013-11-08