基于压缩感知的SAR-GMTI实现
2014-04-26张道成
张道成,彭 磊
(1.解放军92785部队,秦皇岛 066200;2.解放军91404部队,秦皇岛 066001)
0 引 言
压缩感知(CS)理论[1-4]指出只要信号在某个变换空间具有稀疏性,就可以突破奈奎斯特采样定律的限制以较低的频率采样信号,而且可以以高概率重构该信号。将该理论应用于宽带信号处理中,就可以大大缓解采样、存储、传输的压力。目前该理论已经广泛应用于雷达[5-6]、无线传感网络[7]、图像采集设备开发[8]、医学图像处理[9]、遥感图像处理[10]等领域中。对于合成孔径雷达-地面动目标指示(SAR-GMTI)问题来说,其观测场景较大,当场景中强反射点较少时,信号具有稀疏特性,此时可以将压缩感知理论应用于SAR-GMTI中,以解决系统中数据采集、存储与传输的问题。
1 压缩感知的基本原理
传统信号压缩理论框架如图1所示,首先对模拟信号进行奈奎斯特采样得到大量的采样数据,然后对采样数据变换得到少量的大系数和许多小系数,对其中较大的系数和对应位置进行编码、存储、传输,最后对接收信号编码反变换得到恢复信号,这种高速采样后再压缩的过程给硬件系统带来了很大的压力,浪费了大量的采样资源。

图1 传统信号压缩理论框架
不同于传统信号压缩过程,压缩感知理论在采样的同时实现压缩,避免了对采样资源的浪费,其理论框架如图2所示。
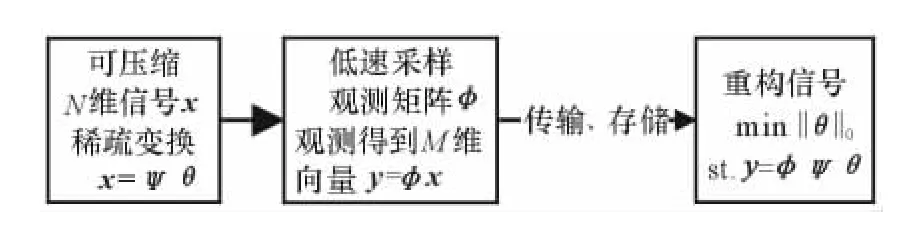
图2 压缩感知理论框架
首先,如果信号x∈RN在某个正交基Ψ上的投影是稀疏,即θ=ΨTx只有K(K≪N)个非零系数(或远大于零的系数)。则可以设计一个平稳、与变换基Ψ不相关的M×N(M<N)维观测矩阵Φ,对可压缩信号x进行降维观测得到M维观测值y=Φx=ΦΨθ。这个M维观测向量保持了重建信号所需的信息,可直接传输、存储。在恢复信号时,通过求解l0范数(非零元素的个数)意义下的优化问题,在满足y=ΦΨθ的条件下min‖θ‖0,得到变换系数的估计值,如有需要可以进行反变换=恢复原始信号。
目前,压缩感知理论研究主要集中在以下3个方面:
(1)信号的稀疏表示问题,即寻找变换基,使信号在该变换基上的投影是稀疏的。常用到的稀疏变换基有傅里叶变换基、小波基、chirplet基等。
(2)设计一个平稳、与变换基不相关的观测矩阵,以保证降维观测的过程原信号不被破坏,通常要求观测矩阵满足有限等距约束(RIP)条件[3-5]。常用的观测矩阵有高斯随机矩阵、伯努利随机矩阵、傅里叶随机矩阵、随机采样矩阵等。
(3)设计快速、高效的重构算法。由于l0范数优化问题的数值计算极不稳定,需要对该问题进行转化。当Φ和Ψ满足不相干特性时,可以将求解l0问题转化为l1问题,并能得到相同的解。目前主要恢复算法有基追踪方法、贪婪迭代方法、贝叶斯框架方法等。
在压缩感知的应用中,大部分是以对压缩信号精确重构为目标进行相关研究。但在很多场合是不需要对压缩信号精确重构的。例如,信号检测这样的任务,就不需要对其精确重构,只应用压缩感知得到的少量观测值即可得到信号有无的信息。文献[11]提出了一种直接应用压缩感知采样的信号,不对其重构,进行检测、分类、估计的算法。该方法直接应用统计信号处理中假设检验的方法,得到压缩感知采样后确定信号检测器的形式。在该算法的基础上,将其和广义似然比检验(GLRT)方法结合,来检测具有未知参数的确定性信号。
2 算法流程
未知参数确定性信号压缩感知后应用于不同类型的信号,以线性调频信号为例进行检测。将SAR回波信号分解为距离向和方位向2个一维信号,应用压缩感知后的GLRT方法分别实现距离向脉冲压缩和方位向参数估计。算法流程如图3所示。得到压缩感知采样数据后,先进行距离向脉冲压缩,在距离向将信号能量累积起来,增强信噪比,便于后续方位向处理。由于方位向信号的未知参数较多,在参数估计时运算量较大,因此在距离向能量聚集后,先检测各距离单元内是否有目标存在,对于有目标的距离单元再进行方位向信号参数估计。最后,通过估计的多普勒中心频率信息确定目标的运动状态。具体算法流程如图3所示。
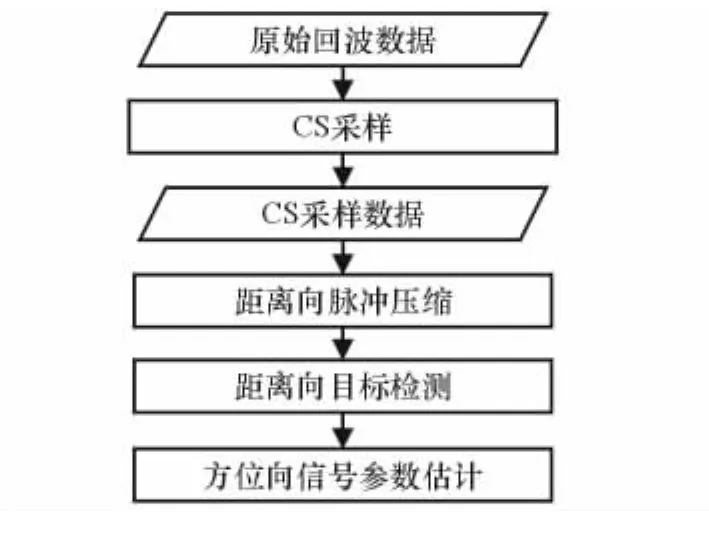
图3 基于压缩感知的SAR-GMTI算法流程
3 仿真实验
实验数据为仿真产生目标回波信号后,在回波信号基础上添加高斯白噪声,得到含有噪声的回波信号。本节应用文献[12]附带光盘中的RADARSAT-1数据作为背景数据,将光盘中数据和仿真生成的运动点目标信号合成作为实验数据。
光盘中数据场景覆盖范围较大,包括陆地、港口、水域等,选取其中水域部分作为背景。读取出水域部分数据后,计算其方差,根据一定的信噪比设定回波信号的幅度,将两部分数据叠加合成新的数据。背景数据的大小为1 024×1 024,仿真产生和背景数据大小相同的运动点目标数据,根据背景数据的标准差确定仿真点目标回波的幅度。在背景数据的基础上添加2个运动点目标,目标的运动参数如表1所示。分别对仿真数据幅度和背景数据标准差的比为-10dB、-15dB的情况进行仿真。

表1 仿真点目标运动参数
对背景数据和合成数据分别成像,当仿真数据幅度和背景数据标准差的比为-10dB时,成像结果如图4所示。图4(a)为背景数据成像结果,其中大部分为杂波(噪声),图4(b)为添加仿真数据后的成像结果,成像方法采用距离多普勒(RD)算法,图中右侧颜色标尺的单位为dB。由成像结果可见,在第200个距离单元,第150个方位单元附近有1个点目标,在第400个距离单元、第300个方位单元附近有1个点目标,这2个点目标分别对应目标1和目标2,由于中心频率的不匹配导致成像结果中产生方位偏移。
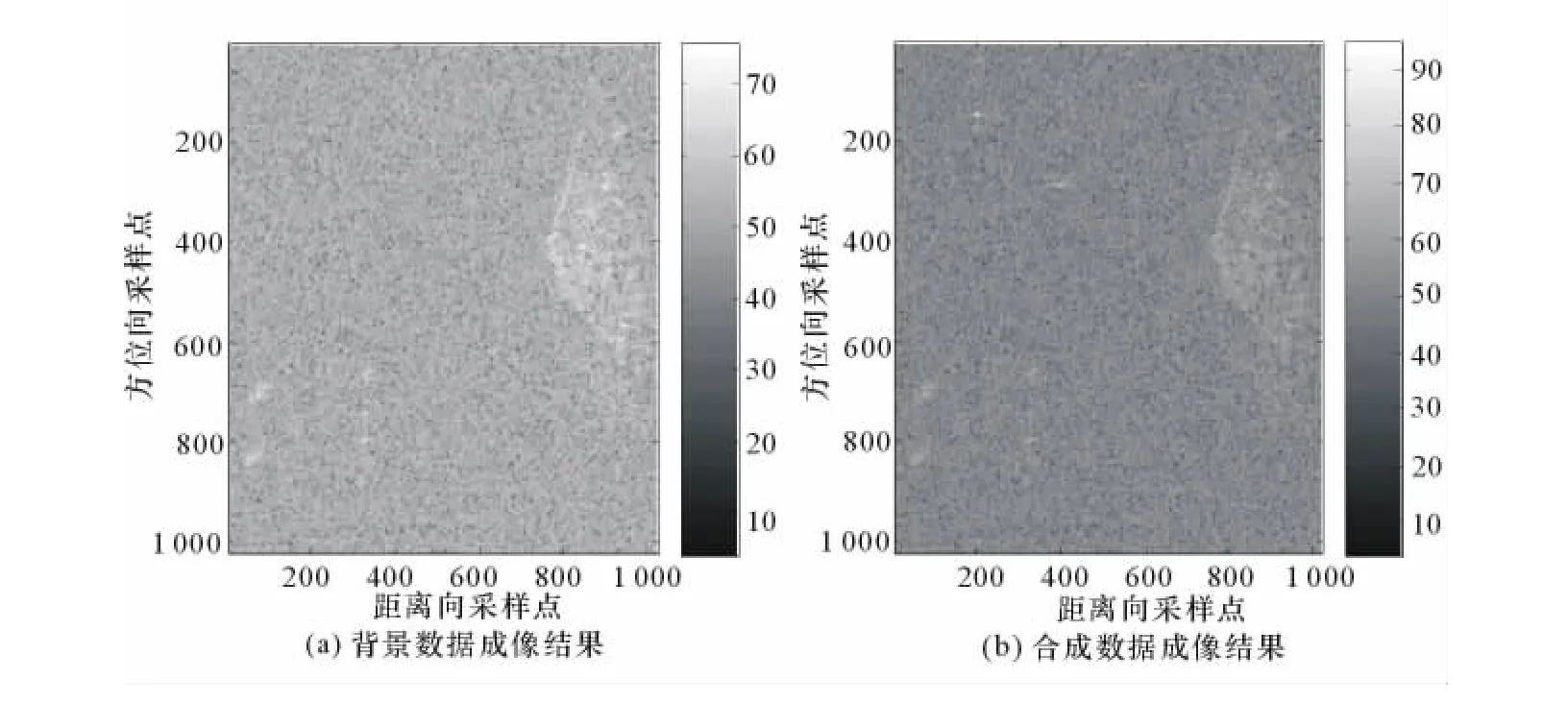
图4 背景数据及合成数据成像结果
对合成数据进行压缩感知采样,将距离向和方位向均压缩为128点,得到观测数据矩阵的大小为128×128。对于采样后得到的观测值应用上节所述运动目标检测方法处理,距离压缩和距离向检测的结果如图5所示,第1个检测门限的虚警概率为0.01。
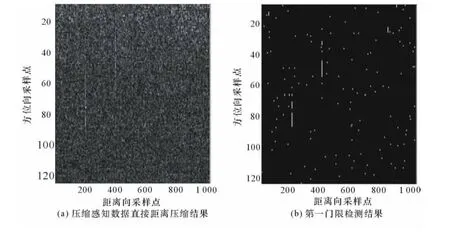
图5 距离压缩和距离向检测结果
对检测得到的所有大于门限的点进行二次门限检测,得到在第200、400个距离单元处存在目标。对该列数据进行方位向参数估计,得到不同延时和中心频率对应的计算值,如图6所示,图6(a)为目标1对应结果,图6(b)为目标2对应结果。其中目标1最大值对应的中心频率为324.07Hz,将中心频率换算成径向速度为9.17m/s;目标2最大值对应的中心频率为25.78Hz,将中心频率换算成径向速度为0.73m/s,由于径向速度过大使其对应的中心频率超出雷达的脉冲重复频率范围,产生速度模糊。

图6 方位向参数估计结果
当仿真数据幅度和背景数据标准差的比为-15dB时,合成数据成像结果如图7所示。在未进行压缩感知采样数据的成像结果中2个点目标仍可见,但应用大小为128×128的压缩感知采样数据在距离压缩后无法检测到这2个点目标。

图7 合成数据成像结果
4 结束语
由此可见,该方法能够在目标个数较少、信噪比较高的情况下,从少量的观测数据中检测出具有径向速度的目标,并在没有速度模糊的情况下,粗略估计目标径向速度。基于压缩感知的SAR-GMTI问题,将二维信号处理分解为距离向信号、方位向信号两个一维信号分别处理。以压缩感知采样信号检测理论为基础,应用上述检测器实现距离压缩、距离向检测、方位检测及参数估计,并通过仿真验证该方法的可行性,实验表明该方法能够在信噪比较高,目标数量较少的情况下,检测到目标的存在。
[1] Donoho D L.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.
[2] Donoho D L,Tsaig Y.Extensions of compressed sensing[J].Signal Processing,2006,86(3):549-571.
[3] Candes E J,Romberg J,Tao T.Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information[J].IEEE Transactions on Information Theory,2006,52(2):489-509.
[4] Candes E J,Tao T.Near-optimal signal recovery from random projections:universal encoding strategies?[J].IEEE Transactions on Information Theory,2006,52(12):5406-5425.
[5] Baraniuk R,Steeghs P.Compressive radar imaging[A].IEEE Radar Conference[C],Boston,2007:128-133.
[6] 方广有,余慧敏.压缩感知理论在探地雷达三维成像中的应用[J].电子与信息学报,2010,32(1):12-16.
[7] Bajwa W,Haupt J,Sayeed A,et al.Compressive wireless sensing[A].The Fifth International Conference on Information Processing in Sensor Networks[C],Nashville,2006:134-142.
[8] Takhar D,Laska J N,Wakin M B,et al.A new compressive imaging camera architecture using optical-domain compression[A].Computational Imaging IV[C].San Jose,2006:1-10.
[9] Lustig M,Donoho D,Pauly J M.Sparse MRI:the application of compressed sensing for rapid MR imaging[J].Magnetic Resonance in Medicine,2007,58(6):1182-1195.
[10]Mai J,Le Dimet F X.Deblurring from highly incomplete measurements for remote sensing[J].IEEE Transactions on Geoscience and Remote Sensing,2009,47(3):792-802.
[11]Davenport M A,Wakin M B,Baraniuk R G.Detection and estimation with compressive measurements[R].Houston,Texas:Rice University,2007.
[12]Cumming I G,Wong F H.Digital Processing of Synthetic Aperture Radar Data:Algorithms and Implementation[M].北京:电子工业出版社,2004.
