减速机鼓形齿联接材料的选择
2014-04-25王孝伟
王孝伟
1 前言
曲靖昆钢嘉华水泥建材有限公司5000t/d生产线于2009年2月投产,在四年的生产过程中,生料磨辊磨减速机(MLX420-01)鼓形齿齿轴、齿套三件套设备故障出现较多。2012年,鼓形齿轴及齿套传动齿轮轴及齿套损坏,给我公司生产带来了极大的损失。
该减速机单台自重106t,若返厂修复或按照正常程序订购备件,整机运输及齿轮备料按程序加工,工期至少需三个月。为了将损失降到最低,我公司一方面和设备制造厂家联系,另一方面想办法尽快修复齿轮轴及齿轮套,恢复生产。
我公司使用的此台减速机为南京高精齿轮集团有限公司2008年在当时的加工能力下开发的最大的减速机,全国只生产了两台,因此,伞齿损坏修复难度较大。为了保护伞齿,在设计时,有意降低了鼓形齿即三件套强度,此处为减速机薄弱环节,易损坏。2010年制造厂家已将MLX420-01辊磨减速机升级为MLXSD420辊磨减速机,MLX420-01辊磨减速机停产后,备件、毛坯均没有库存,修复工期压力更大。整机结构见图1。
在立足公司内部,确保修复后能够稳定生产,并能缩短修复工期,降低损失,在鼓形齿及齿套的具体材料规格未知的前提下,现已找到毛坯材质为42CrMoA的锻件。如果毛坯粗车至每个加工面留5mm余量后,调质处理,加工完成磨齿前对齿面进行高频淬火,能满足要求,就可以立即组织锻件并开始机械制造,既能节约设备原制造厂家按照正常生产程序所需要的大部分时间,又可节约对旧件取样、外送检测确定材质的时间,同时也可避免材质检测结果偏差带来的强度影响。经过查询生料磨及减速机的资料,对减速机鼓形齿三件套工作原理进一步分析,并对材质为42CrMoA的锻件进行强度设计校核。
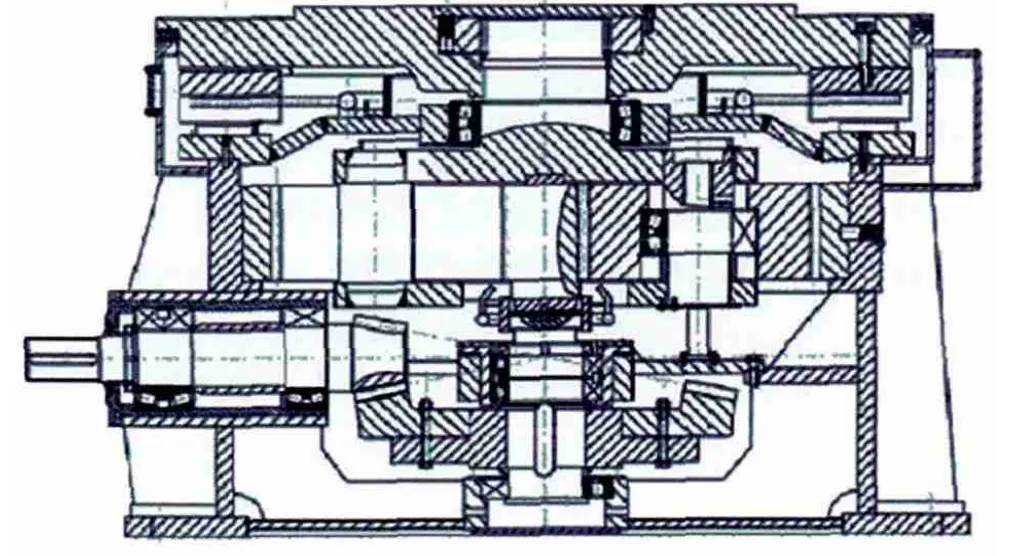
图1 整机结构
鼓形齿联接方式是以沿齿长方向齿厚呈鼓形的外齿轴套和直齿内齿圈组成的一种挠性联接,主要用于被联接的两轴或回转件,允许有一定的轴向位移和轴线偏角。这种联接方式已广泛运用于行星齿轮减速器的内部浮动结构。
采用鼓形齿联接一般具有如下特征:外齿轴套的齿厚呈鼓形,中间厚两端薄,可避免齿端棱角接触,因此允许两轴线有较大的角位移,一般设计为±0.5°;鼓形齿能有效地避免轮齿端部接触引起的应力集中,因此能承受较大的转矩和冲击载荷,过载能力大,工作平稳可靠,在出现同样的角位移情况下,比直齿联轴器的承载能力提高15%~20%,传动效率高达99.7%;鼓形齿不承受轴向力,结构上能补偿运转中的少量轴向位移;鼓形齿结构紧凑,重量和转动惯量较小,工作时产生的不平衡力矩较小。
2 基本原理
外齿轴套的轮齿按其在齿宽方向的截面形状不同可分为直齿和鼓形齿。它与直齿内齿圈的接触情况如图2所示。
直齿加工简单,但允许的偏摆角小,一般≤30′,工作时轮齿的端部容易受载,齿面磨损大,强度和寿命低。
鼓形齿允许的偏摆角较大,轮齿的受力情况好,偏转角变大,强度和寿命均较直齿有所提高。
齿廓为鼓形齿的外齿轴套,工作中当轴线出现相对角位移ω时,则每转一圈,外齿轴套的齿和内齿圈的齿之间就有相对运动,为齿的摆动运动和翻转运动,这两种运动在轮齿啮合的半周中会出现“纯摆动—复合运动—纯翻转—复合运动—纯摆动”的循环运动过程。若将轮齿沿啮合圆周展开,则各齿之间的相对位置如图3所示。
为避免轮齿摆动引起轴套外齿齿顶与齿圈内齿齿根的位置变化出现干涉,可根据相对角位移和外齿齿宽来确定外齿的齿顶圆弧Ra。
轮齿出现翻转运动时会产生切向位移,此位移所需要的空间由齿间侧隙来保证。一般取纯翻转的90°齿位的位移量为计算最小侧隙jnmin的依据。

图2 轮齿截面形状和接触状态
3 基本计算原理
3.1 几何尺寸计算
(1)曲率半径
鼓形齿的承载能力和允许的偏移量或摆角与齿的曲率半径有直接关系。从提高承载能力角度而言,曲率半径愈大愈好,而从加大允许摆角而言,曲率半径则愈小愈好。
为了保证鼓形齿外齿轴套的轮齿有良好的接触和弯曲强度,一般推荐工作长度的降低系数为0≤q≤0.5;当ω≤25°时,则R值等于分度圆半径,即R=r;当25°≤ω≤6°时,R=0.5r。根据0≤q≤0.5,则原始齿形移动半径R值为:
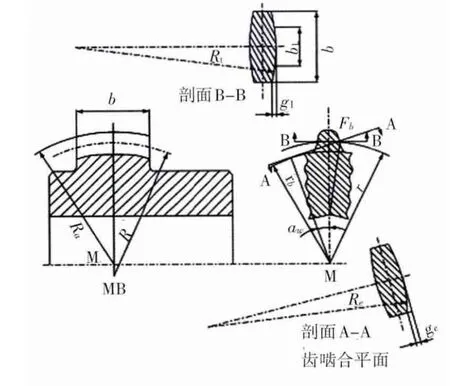
图4 圆弧形曲面的曲率半径
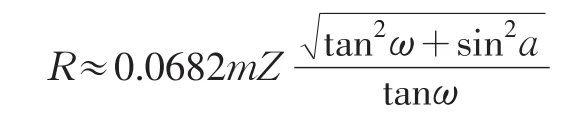
当R≤r时,轮齿端部的齿高大于中部齿高,滚刀铣切时可能会出现根切;在轮齿的摆动过程中轴套的外齿齿顶与齿圈的内齿齿根会出现干涉,此时需进行修顶或使顶圆半径Ra和齿形移动半径R同心。
滚齿加工时,分度圆切向曲率半径Rt见图4剖面BB所示。
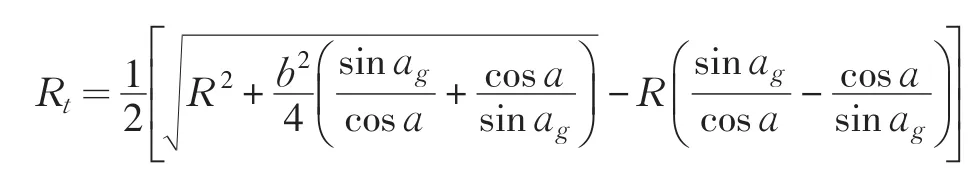
分度圆法向曲率半径Re见图4剖面A-A所示。

式中:
ag=a+a*
a*——加工角
令Rt=Φt·R,Re=Φe·R,Φt、Φe为曲率系数,数值见表1。
(2)其他尺寸
鼓形齿齿式联接的定心方式有外径定心和齿侧定心(齿形定心)两种,如图5所示。外径定心是以外齿轴套齿顶圆直径da1定心,它与齿圈的内齿齿根圆名义直径值相等(da1=df2),并做成半径Ra1=da1/2的球面。直径之间的配合一般采用F9/h8或F8/h7;齿侧定心时,直径da1和df2之间有较大间隙,外齿轴套的齿顶圆可以是球面的,也可以是圆柱的。齿侧定心有自动定心作用,有利于齿间载荷分布。
鼓形齿联结的内齿和外齿的啮合关系如图6所示。其齿形角α=20°~30°,最常用的是α=20°。可以采用变位啮合,内齿轮的变位系数x=0.3~0.5,外齿轮的变位根据保证摆角ω的最小侧隙而定。经变位后,内齿和齿根的抗弯截面较大,并使两者趋于等强度,有利于提高外齿套的齿根强度。对于齿数较少的内齿圈,变位还有利于避免插齿时的顶切现象。变位后齿顶厚度应保证Sa1≥0.4m。
分度圆直径:
d1=d2=mz
齿顶圆直径:
da1=mz1+2m(ha1*+x)
da2=mz2+2m(ha2*+x)
齿根圆直径:
df1=mz1-2m(1.25-x)
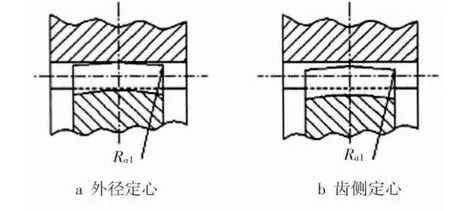
图5 定心方式

图6 啮合关系

表1 曲率系数Φt、Φe

表2 MLX420-01减速机技术参数

表3 MLX420-01减速机鼓形齿参数
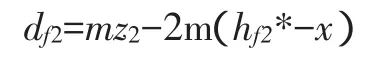
齿廓平均压力角:
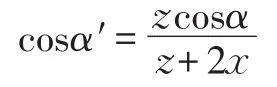
ha1*和hf2*按不同的定心方式确定。
外径定心:
ha1*=hf2*=0.8~1
齿侧定心:
ha1*=0.8~1,hf2*=1.25
ha2*与内齿圈的齿数有关,一般取ha2*=0.6~1,通常取0.8和1。
(3)齿侧间隙
鼓形齿联接的齿侧间隙应不受齿轮的加工、装配误差影响,保持轴线倾斜时轮齿翻转运动所需要的空间。因此,齿侧间隙主要由以下两部分组成:
jn=jnmin+δjn
分度圆切向最小间隙:
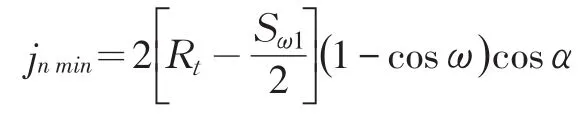
补偿制造误差的侧隙δjn可直接从相关手册中查得。
3.2 强度计算
鼓形齿齿式联接的失效形式主要是齿面磨损和点蚀,出现断齿的可能性较小。在设计时通常只需计算轮齿的齿面出现接触强度,对轮齿的弯曲强度可根据实际情况判断是否需要进行计算。
计算鼓形齿的接触应力和形变时,一般做无轴线偏移简化处理,简化算法依据传统的赫兹理论,即利用线接触的平行圆柱体代替某一具体啮合位置的实际齿面。鼓形齿的接触啮合方式不同于其他齿轮传动的接触啮合:在齿轮传动中,曲率半径为啮合点处的齿廓曲率半径,承载长度为沿齿长方向(齿宽)有效接触长度;鼓形齿曲率半径取分度圆法向切面曲率半径Re,承载长度为沿齿高方向有效接触高度h,如图7所示。
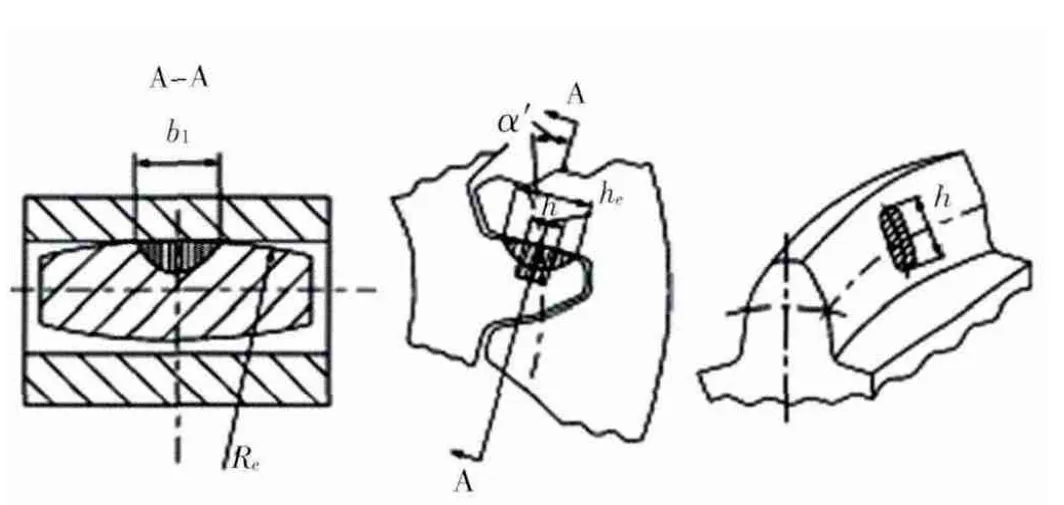
图7 鼓形齿的赫兹接触
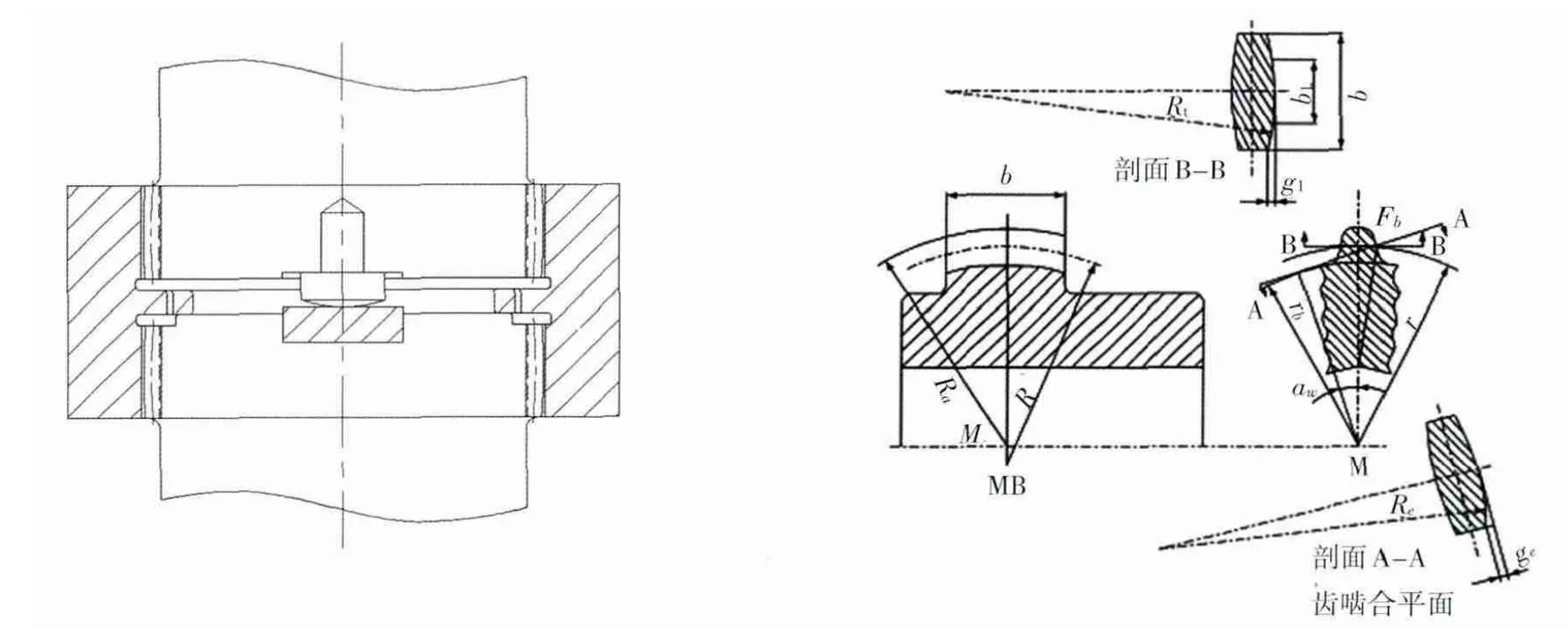
图8 鼓形齿联接示意图
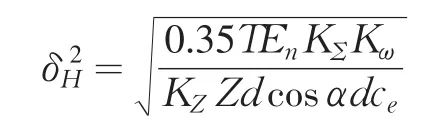
式中:
T——计算转矩
En——弹性模量
KΣ——综合系数,与使用工况、工作速度、制造精度等有关
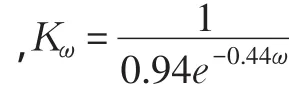
KZ——轮齿间的载荷不均系数,一般取0.75~0.8
鼓形齿接触状态复杂,通常在实际工程问题上采用简化算法计算其承载能力,必要时还可通过实验方法来确定附加载荷的影响。另外也可采用数值计算方法,常用的方法为有限元法和边界元法。
4 MLX420-01辊磨减速机相关技术参数
(1)MLX420-01减速机技术参数(表2)
(2)MLX420-01减速机鼓形齿参数(表3)
5 强度计算(参见《现代机械设计手册》)
(1)齿面接触强度应满足以下条件:
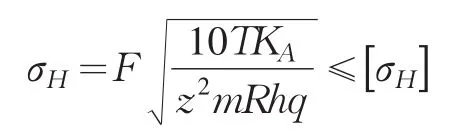
式中:
σH——计算接触应力,MPa
F—— 压力角系数,α=28°时,F=1174
T——传递扭矩,T=274350N·m
KA——使用系数,KA=2
z——齿数,z=40
m——模数,m=8mm
R——位移圆半径,R=600mm
h——实际接触齿高,一般取h=1.5~1.8m
q——轴线倾斜角系数,q=60
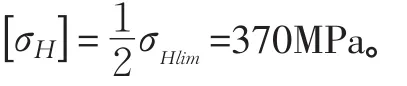
计算结果如下:
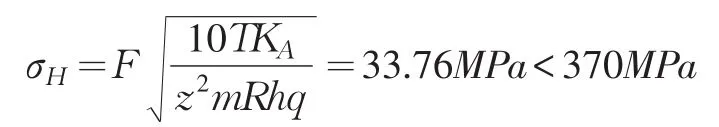
(2)剪切强度应满足以下条件:

式中:
τ——计算剪切应力,MPa
d——分度圆直径,d=320mm
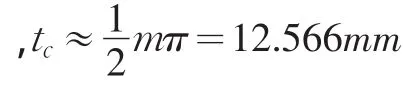
[τ]——许用剪切应力,42CrMoA材质,调质处理,[τ]=332.5MPa。
其他代号同前,计算结果如下:

(3)联接内齿套的齿面接触强度和轮齿剪切强度与鼓形齿轴相同,考虑到内齿套为直齿(无鼓形量),另外校核其齿面挤压强度。

式中:
σP——计算挤压应力,MPa;
Km——轮齿载荷分布系数,Km=1.5
Kw——轮齿磨损寿命系数,Kw=1.0
[σP]——许用挤压应力,42CrMoA材质,调质处理,[σP]=280MPa
其他代号同前,计算结果如下:
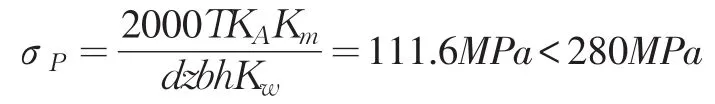
6 结论
综上可见,MLX420-01辊磨减速机的内部鼓形齿选用42CrMoA材质,调质处理,联接强度满足要求,按照破损件尺寸进行制造。现使用时间超过三个月,设备平稳运行。
[1]秦大同,谢里阳.现代机械设计手册[M].北京:化学工业出版社,2011.
[2]成大先.机械设计手册[M].北京:化学工业出版社,2007.
[3]彭文生,王均荣.机械设计[M].武汉:华中理工大学出版社,1996.
[4]黄华良,彭文生刘凯.机械设计基础[M].长沙:湖南科学技术出版社,1992.
[5]黄纯颖.工程设计方法[M].北京:中国科学技术出版社,1989.
[6]邓文英.金属工艺学(第三版)[M].北京:高等教育出版社,1991.
