气体钻井API钻铤螺纹多轴疲劳寿命研究

2014-04-23李群生王希勇林铁军朱化蜀谢晓永

石油钻采工艺 2014年3期

李群生王希勇林铁军朱化蜀谢晓永

（1.中石化西南油气分公司工程技术研究院，四川德阳 618000；2.西南石油大学油气藏地质与开发国家重点实验室，四川成都 610500）

国内外大量现场资料表明，钻柱破坏最常见的形式是疲劳破坏［1］。气体钻井在大钻压作用下，常发生钻铤螺纹疲劳断裂失效［2-3］。气体钻井中不论是钻杆还是钻铤都承受着拉压、弯扭等多种外力的综合作用，运用单轴疲劳理论研究其疲劳寿命不能完全考虑气体钻井中钻柱的运动特性和外载综合作用。因此，本文运用多轴疲劳寿命理论研究气体钻井中钻柱在拉压、弯扭共同作用下的疲劳寿命。

1 钻铤螺纹多轴疲劳寿命理论

多轴疲劳是多向应力或应变作用下的疲劳，在多轴循环加载条件下，有2个或3个应力（或应变）分量独立地随时间发生周期性变化［4］。近年来，多轴疲劳寿命理论在国内航空航天、核电、交通运输等行业工程中有大量应用［5-9］，而应用到气体钻井钻柱疲劳寿命领域还未见报道。

1.1 钻铤材料多轴循环应力应变关系

实际钻井过程中作用在钻柱上的循环作用力非常复杂，本文假设作用在钻柱上的拉压、弯扭循环载荷为一个比例加载，钻柱上的应力张量各分量成比例增大，应力主轴方向保持不变。由于多轴比例加载下的等效循环应力应变关系与单轴加载情况是一致的［4］，所以钻铤材料多轴比例加载作用下的循环应力应变关系式为

式中，Δσeq和Δεeq分别为Von-M ises等效应力幅、等效应变幅；E为材料弹性模量；n为钻铤螺纹材料循环应变硬化指数；K为钻铤螺纹材料循环强度系数；b为钻铤螺纹材料疲劳强度指数；c为疲劳延性指数；σf为钻铤螺纹材料疲劳强度系数；εf为钻铤螺纹材料疲劳延性系数［10］。

1.2 基于应变的疲劳破坏准则

钻铤用42CrMo钢满足Coffin-Manson方程［11］，该方程以塑性应变作为损伤参量来估算多轴疲劳拉压低周疲劳寿命，其表达式为

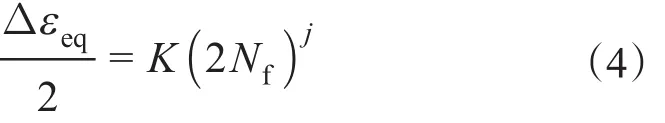
式中，K为材料的循环强度系数（疲劳延性系数），可由单轴低周疲劳实验得到；Nf为材料疲劳寿命；j为疲劳延性指数。

1.3 基于M ises屈服准则的多轴疲劳寿命预测方法

利用等效应变作为参量，结合Coffin-Manson方程得出寿命预测公式，估算出多轴状态下的疲劳寿命［4］，其表达式为

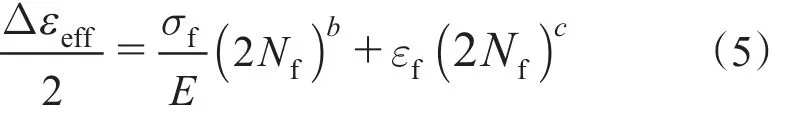
其中，等效应变为

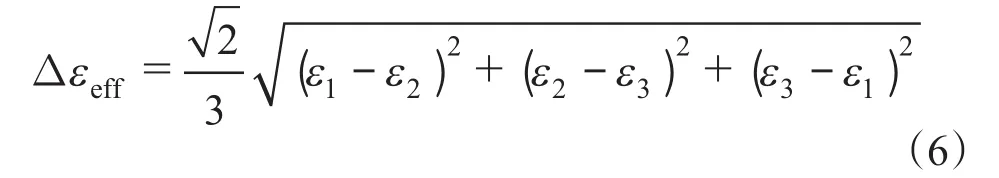
式中，ε1、ε2、ε3为主应变。

1.4 基于临界面法的多轴疲劳寿命预测方法

使用多轴疲劳寿命的临界面法预测疲劳寿命时，首先找出临界损伤平面，然后将其平面上的法向应力（应变）构造多轴疲劳损伤参量，建立疲劳寿命预测方程。Lohr通过对薄壁件进行拉扭复合比例加载实验［4］，得到多轴疲劳寿命预测表达式

式中，Δγ为法向最大剪应变幅；εn为法向应变。

2 API钻铤螺纹多轴疲劳寿命研究

根据气体钻井现场调研和钻柱动力学分析，受压弯曲的Ø177.8 mm钻铤承受周期出现的剧烈轴向振动和瞬时冲击作用力［2］，造成钻铤螺纹疲劳断裂失效事故常发。下面以Ø177.8 mm钻铤螺纹为研究对象进行API螺纹的多轴疲劳寿命研究。

2.1 建立钻铤螺纹有限元模型

根据文献［12］，把Ø177.8 mm API钻铤螺纹所受到的弯矩、扭矩及钻压波动数据作为钻铤螺纹多轴比例加载外载荷（图1）。根据中国石油天然气行业标准［13-14］，用Pro/E三维建模软件建立了Ø177.8 mm钻铤V-0.038R螺纹牙型的三维实体模型，并建立相应的有限元模型（图2）。模型中，首先在Ø177.8 mm钻铤施加70 kN·m的上扣扭矩［15］，再施加如图1所示的气体钻井周期压、扭、弯外载荷，从而得到API钻铤螺纹在气体钻井周期外载作用下的应力应变结果。

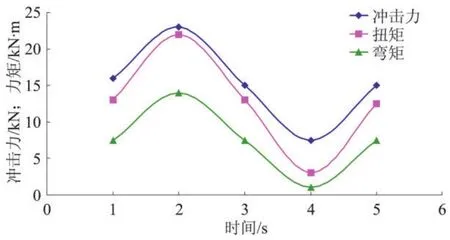
图1 气体钻井Ø177.8 mm钻铤周期多轴外载荷

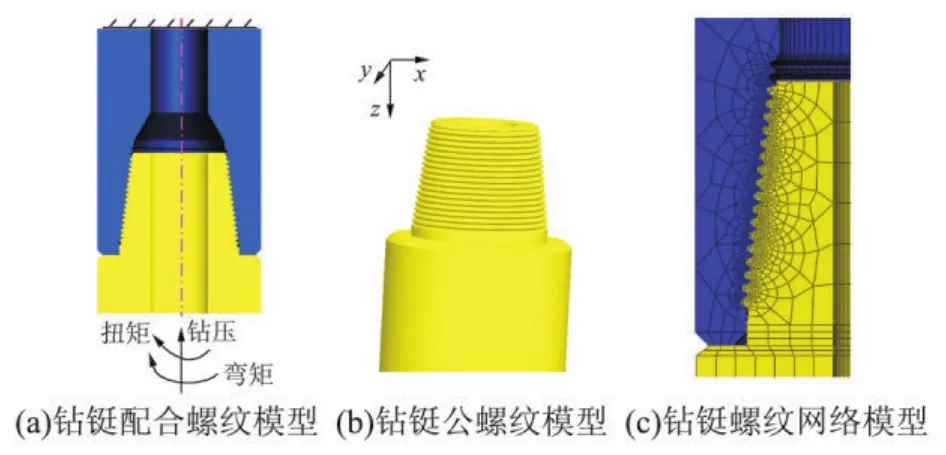
图2 钻铤螺纹有限元分析模型

2.2 钻铤螺纹在多轴载荷作用下的应力应变分布

根据有限元模型计算得到Ø177.8 mm钻铤存在周期最大外载和周期最小外载共同作用的循环应力应变。由图3可见，Ø177.8 mm钻铤API螺纹最大应力值为906 MPa，发生在母螺纹从台肩面开始的倒数第2扣螺纹根部；公螺纹最大应力值约为600 MPa，出现在公螺纹小端第1扣螺纹区域，公母螺纹各扣的应力分布极不均匀；周期最小气体钻井载荷作用下的公母螺纹应力分布云图与周期最大外载作用下相同，但母螺纹最大应力值约为820 MPa，公螺纹最大应力值约为530 MPa。

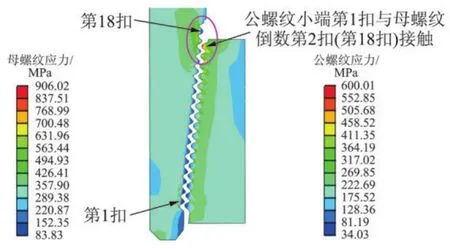
图3 钻铤公母螺纹在周期最大外载作用下的应力分布

2.3 钻铤螺纹多轴疲劳寿命预测

从图3可见，多轴疲劳寿命临界面在母螺纹倒数第2扣螺纹根部。因此，取母螺纹在气体钻井周期最大加载和最小加载作用下的临界面最大主应变、中间主应变和最小主应变，可得到API螺纹临界面的最大主应变幅、中间主应变幅和最小主应变幅；根据临界面3个主应变幅可计算得到基于Von-M ises等效应变法的等效应变幅值和基于Lohr临界面损伤模型的等效应变幅值的多轴疲劳损伤参量；进一步根据式（5）和式（7）计算得到钻铤母螺纹在拉压、弯扭周期作用下的基于Von-M ises等效应变法和基于Lohr临界面法的多轴疲劳寿命（见表1）。

表1 钻铤螺纹临界面应变幅和疲劳寿命值

从表1可见，API钻铤螺纹以Von-M ises应变法和Lohr临界面损伤模型计算得到钻铤螺纹疲劳寿命值都约为2×105次，多轴疲劳寿命很短，极易造成钻铤螺纹多轴疲劳断裂。据此可知，气体钻井API钻铤螺纹在大钻压下可能出现快速失效，建议开发适合于气体钻井的双台肩螺纹钻铤以提高钻铤多轴疲劳寿命。另外，Von-M ises应变法和Lohr临界面模型的多轴疲劳寿命预测方法在计算气体钻井钻铤低周疲劳时预测结果比较接近，而且Lohr临界面模型计算结果更趋安全。