辽宁电力系统冰区分级研究

司红代，朱义东，韩洪刚，郝建成

(1.沈阳工程学院，辽宁 沈阳 110136;

2.国网辽宁省电力有限公司电力科学研究院，辽宁 沈阳 110006)

辽宁电力系统冰区分级研究

司红代1，朱义东2，韩洪刚2，郝建成2

(1.沈阳工程学院，辽宁 沈阳 110136;

2.国网辽宁省电力有限公司电力科学研究院，辽宁 沈阳 110006)

将辽宁省近30年全部观冰站的覆冰厚度观测数据折算到标准状态下覆冰厚度进行高度和线径修正，利用克里格插值技术计算得到覆盖全省地理范围的覆冰厚度数据，对全省不同地区的覆冰数据利用极值模型进行重现期覆冰厚度计算，首次利用覆冰数据法得到不同重现期覆冰厚度分布图，并对基于不同气象参数的回归法覆冰分级进行了探讨。

覆冰数据;冰区分级;极值模型

输电线路在覆冰严重时容易造成倒塔、断线等严重事故，覆冰后的导地线在风力作用下还容易发生舞动进而形成停电故障或次生倒塔断线事故［1-2］。

目前辽宁省内电力设计部门在输电线路设计过程中往往依照整个地区粗略覆冰情况开展设计，并无详细的冰区划分数据可以参照。在覆冰较轻地区如采用过大的线路覆冰设计裕度将造成资源浪费，但如果覆冰设计偏低，则容易因设计标准过低引发事故［3］。基于此开展了省内冰区细化分级的研究，基于覆冰观测数据完成了电力系统冰区分级，并对气象回归法进行了计算和探讨。

1 数据资料选取

采用辽宁省内11座观冰站导线1980年以来年结冰资料，选取导线结冰发生前2日、前1日及当日的最高气温、最低气温、日照日总量、日平均相对湿度、日平均水气压、日平均气温、日平均风速、日20:00风向、日14:00风向、日08:00风向、日02:00风向、日降水量作为回归变量进行研究分析。

经过统计分析收集到辽宁省过去30年发生的有效雾凇观测450次，雨凇观测116次。同时为弥补观测资料不足，还参考国网辽宁电力近10年输导线路舞动频次分布图对冰区重现期进行修正。

2 重现期覆冰厚度计算

根据辽宁省导线积冰站点观测记录历史较长的特点 (观冰数据年代序列大于30年)，尝试采用覆冰数据法确定不同重现期设计冰厚。

2.1 标准冰厚计算

由于辽宁导线积冰资料观测中关于积冰重量的记录相对较少 (按文献《地面气象预测规范》，当积冰直径大于一定数值时才测定重量，故个别气象站历史上无冰重观测)，因此采取长短径尺寸计算公式进行标准冰厚计算，即:

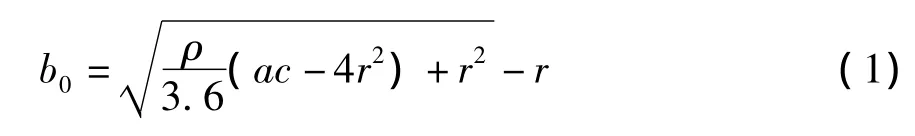
式中 b0——标准冰厚，mm;

ρ——实测或调查覆冰密度，g/cm3;

r——导线半径，mm;

a——覆冰长径，mm;

c——覆冰短径，mm。

ρ在雨凇和雪凇时可粗略选取不同数值，由于雨凇比其他形式冰粒坚硬透明，密度ρ取0.85 g/cm3，而和雨凇相似的雾凇密度ρ只有0.25 g/cm3。当覆冰重量数据较全时，精确计算ρ的公式:

式中G为冰重，g/m。

通过计算得出辽宁省11座观冰站历史最大冰厚及标准冰厚，最大冰厚如表1所示。

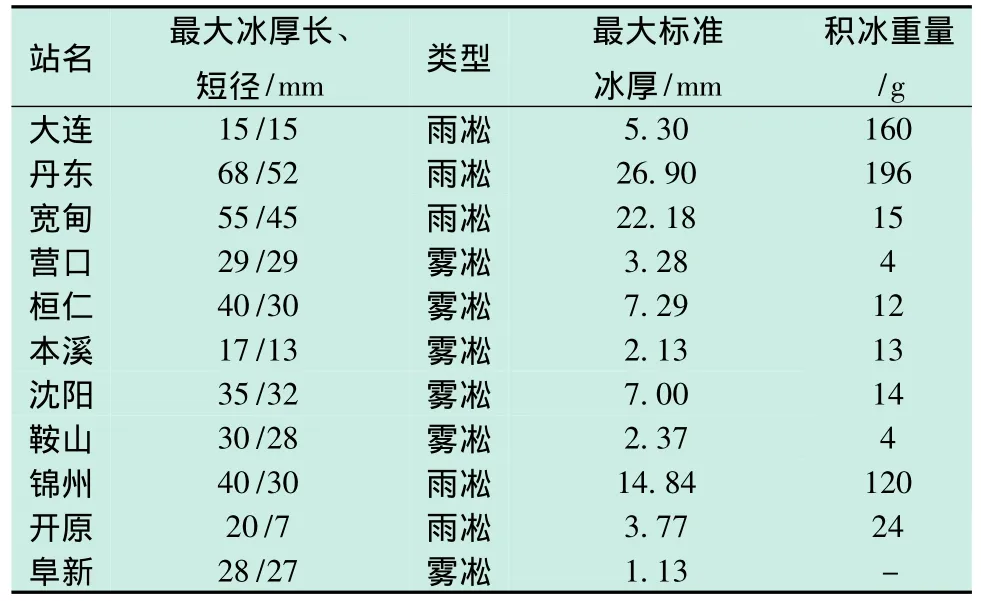
表1 辽宁省11座观冰站历史最大冰厚及标准冰厚

2.2 高度和线径修正

表1标准冰厚为测量得到的最大冰厚，为进行标准分析和具备可比性，需要考虑不同时期、不同站点悬挂测试导线的高度和线径的影响。按相关气象规范要求，将冰厚统一修正为离地10 m、直径为26.8 mm导线的覆冰冰厚。高度与线径修正系数计算公式:

式中 Z——设计导线悬挂高度，m;

Z0——实测或调查覆冰导线悬挂高度，m;

α——指数，与风速、含水量与捕获系数有关，无实测资料时α可取0.22。

辽宁地区悬挂的观冰导线离地高度为2 m，则辽宁地区高度修正系数为

Kh=(10/2)0.22=1.43

线径修正系数计算公式:

式中 φ——设计导线直径，mm;

φ0——实测或调查覆冰的导线直径，mm。

1980～2010年观冰导线线径为4 mm，则:

Kφ1=1-0.126ln(26.8/4)=0.76

2011年后，线径改为标准导线26.8 mm，则:

Kφ2=1-0.126ln(26.8/26.8)=1

经过高度与线径修正后的标准厚度为

2.3 计算不同重现期设计冰厚

将修正后的冰厚数据进行统计整理，根据概率分布模型计算不同重现期的冰厚。

概率分布模型采用极值Ⅰ型分布，计算公式:

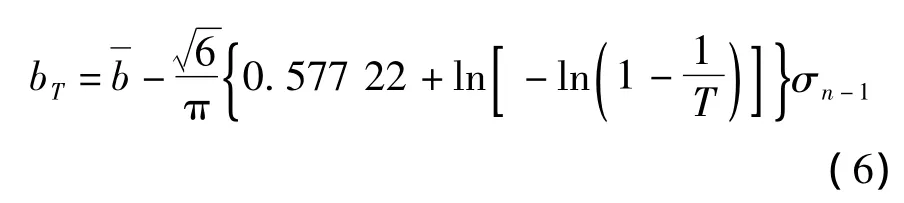
根据概率分布模型采用极值Ⅰ型分布，计算出已有导线积冰观测站的30、50、100年重现期冰厚。计算结果如表2所示。

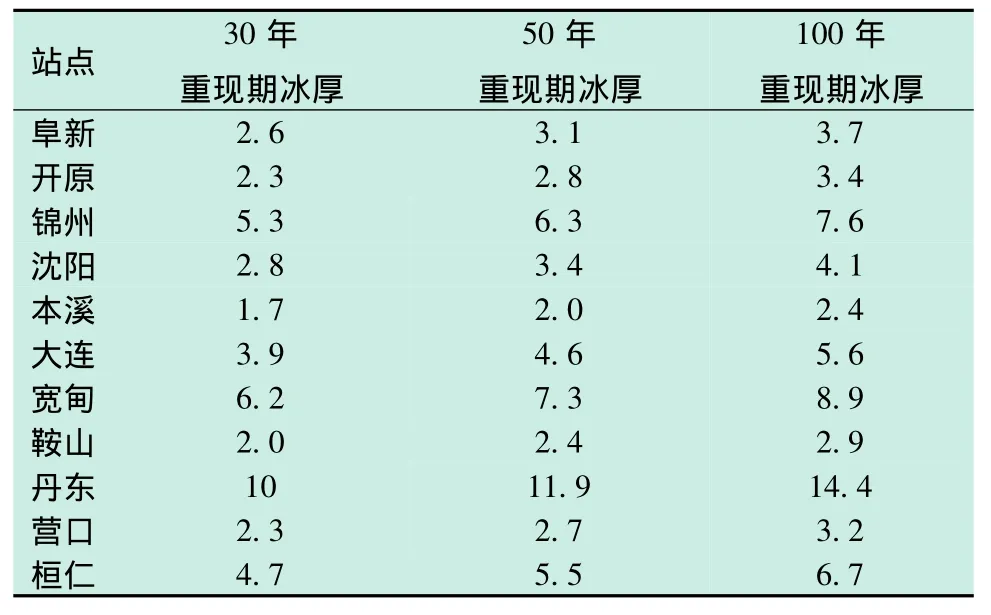
表2 辽宁省各监测站导线结冰标准冰厚 mm

2.4 微地形影响修正

对于风口、迎风坡等对线路覆冰有影响的特殊地形，应考虑不同地形的修正系数Kh，其取值应根据实测资料分析确定，本文按相关标准推荐值选用修正系数［4］。

使用绘图软件内置的克里格插值设计，将微地形冰厚计算结果进行空间插值，并绘制冰区图。根据线路设计和运行的实际经验，对所绘冰区图进行修正。

经过微地形修正及参考导线舞动分布图后修正得到的重现期冰厚如表3所示。

表3 地形修正后辽宁省各监测站导线结冰标准冰厚mm

3 辽宁省冰区分布特征及冰区分级

3.1 辽宁省导线积冰发生频次空间分布

通过统计辽宁省历史上 (1980～2011年)11座导线积冰观测站的导线积冰观测数据，可以看出辽宁地区导线积冰发生次数最多的是丹东地区，累计积冰次数达103次。导线积冰发生的高值区有两个，一个是东南沿海以及辽东半岛北部地区 (包括丹东、宽甸、营口、盖州、瓦房店等市县)，另一个是辽宁北部地区 (包括沈阳、铁岭的大部分地区)。近30年辽宁省导线积冰日数空间分布如图1所示。

图1 近30年辽宁省导线积冰日数空间分布

3.2 辽宁省导线积冰发生频次的时间分布

导线积冰日数年际间波动较大，没有明显的趋势性，波动范围为5～55 d。1993年是辽宁省导线积冰现象最多的年份，雾凇最多的年份同样发生在1993年，雨凇出现最多的年份为1992年、1993年。雾凇每年均有发生，而雨凇个别年份没有出现，除1987年外每年雾凇日数均多于雨凇日数。辽宁省导线积冰现象一般发生在10月至次年4月，1月最多，1、2、12月雾凇日数明显多于雨凇，3、10月相当，4、11月雨凇多于雾凇，特别是11月雨凇明显居多。

3.3 不同重现期冰区分级

由表3可见，通过ARCGIS地理信息平台中的克里格插值法，将11个观冰点的数据插值到全省，得到30年、50年、100年重现期冰区如图2～图4所示。

可见，主要冰区分布在辽宁东部山区、辽宁南部沿海、辽宁西部及西南部沿海地区，这些地区主要受地形及水体分布的影响，其中丹东地区是导线积冰严重地区。

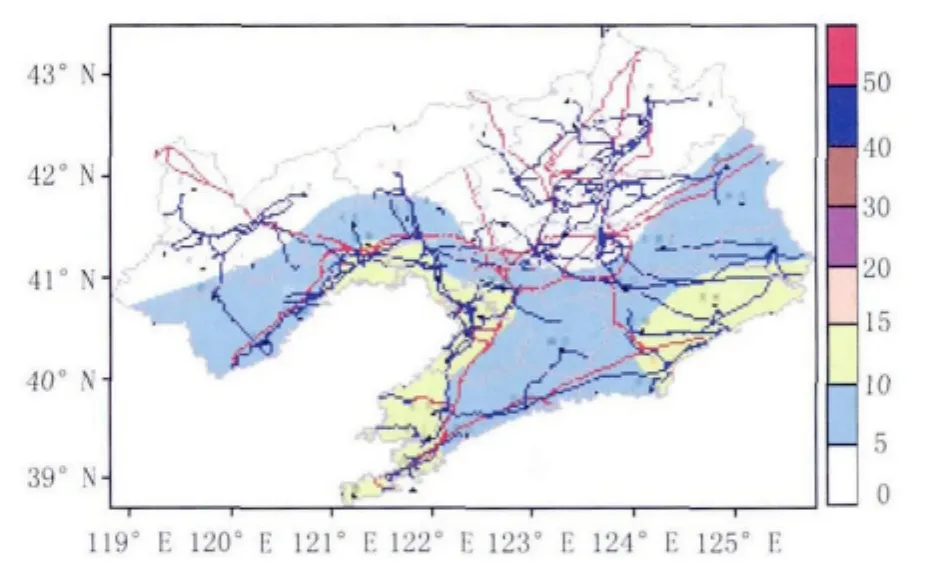
图2 经验修正后的30年冰区重现期分布

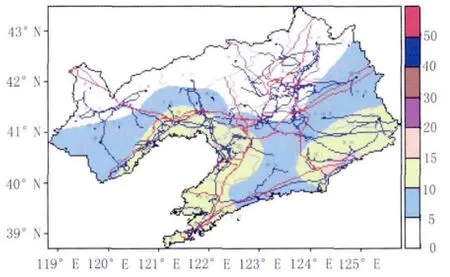
图3 经验修正后的50年冰区重现期分布

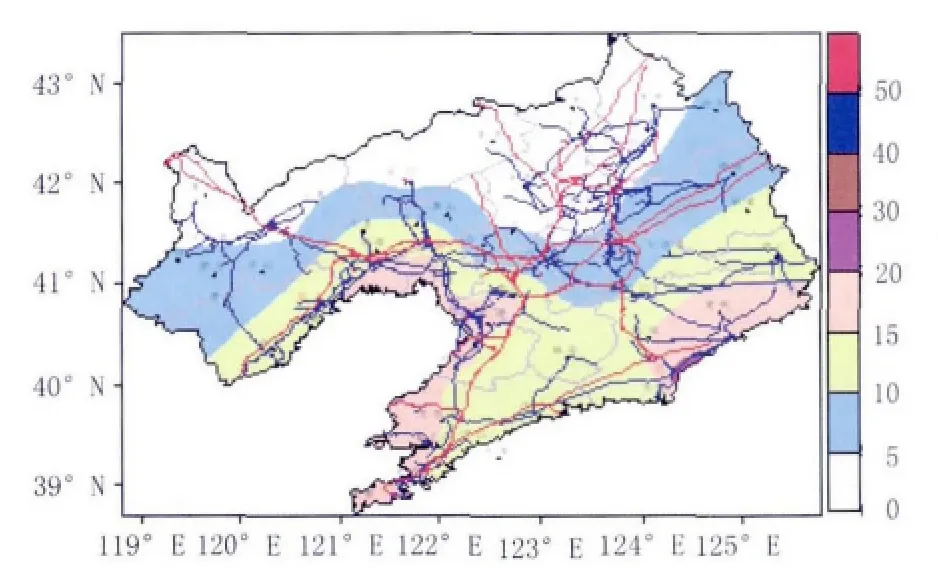
图4 经验修正后的100年冰区重现期分布

4 统计回归方法分析

当观测数据的年代序列较短，但具有较详细的与覆冰形成相关气象因子和地理因子资料时，可利用逐步回归法建立导线覆冰厚度与环境因子回归模型，并将确定的回归模型运用到本地区地面气象观测站，从而确定地面气象观测站所在位置的历史覆冰冰厚［5］。

气象预报中，常需要从可能影响预报量的许多因素中挑选一批关系较好的作为预报因子，逐步回归分析方法就是针对以上需要能够保证在已选定的一批因子中得到最优的回归方程的方法，包含以下方案。

a. 逐步剔除方案

从包含全部变量的回归方程中逐步剔除不显著的因子，即每次仅比较因子的方差贡献 (偏回归平方和)，记为

从Vk(k=1，2，…，p)中选出方差贡献最小者，记为Vmin，再做F检验。

b. 逐步引入方案

在一批待选的因子中，考察其对预报量y的方差贡献，挑选所有因子中方差贡献最大者，经统计检验显著的，引入回归方程。

c. 双重检验的逐步回归方案

逐步剔除计算量较大，逐步引入虽然计算量相对小一些，但不能保证最后的方程是最优的。而双重检验逐步回归方案则综合二者优点克服其缺点的方案。基本思路如下:将因子依次引入，引入因子的条件是该因子的方差贡献是显著的。同时，每引入一个新因子后，要对老因子逐个检验，将方差贡献变为不显著的因子剔除。该方案是利用求解线性方程中求逆同时并行的方法，使计算因子方差贡献和求解回归系数同时进行，计算比较简便，且每一步都做了检验，最后所得方差中所有因子都是显著的。

由于该方法简便可靠，故在此次电网冰区分布图绘制中采取该方案。利用Matlab作为统计分析工具，计算步骤如下。

显著性水平:α=0.10

引入变量的临界值:Fin=4.0剔除变量的临界值:Fout=4.0拟建立回归方程:

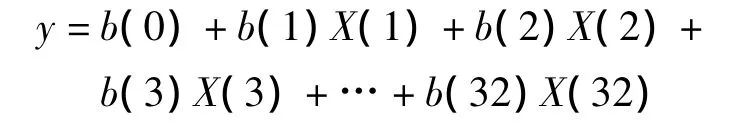
第1步准备工作:从标准化变量出发，建立求标准回归系数的标准方程组，合并预报量(y)与待选预报因子(X(1)，X(2)，X(3)，…，X(32))组成一个方阵，开始做逐步回归的计算。

第3步剔除或引入变量:只在引入3个变量后才考虑前2个引入因子是否贡献不大，同样利用公式分别找出已引入项中Vk绝对值最小者和未引入项中Vk绝对值最大者，分别引入两者检验值Fout(kin)、Fin(kout)，若Fout(kin)＞Fout，则已引入的第kin项不能剔除，反之则可剔除，而若Fin(kout)＞Fin则未引入第kout项可被引入。

最后筛选出3个引子分别为X(4)，X(15)，X(32)，建立回归方程:

2.328 41 × 10-6＜＜ 0.05，残差均方 RMSE=0.957 074，由于R2检验值偏小，且选出的预报因子数量偏少，此方法较预期有一定偏差。

因此，辽宁地区现有条件下不适合采用参量逐步回归分析方法。

5 结论

a. 基于30年全省观冰站的覆冰厚度数据，通过标准冰厚计算和地形、线径修正计算得到覆盖全省地理范围的覆冰厚度数据。利用极值模型进行重现期覆冰厚度计算，得到全省电力系统不同重现期覆冰厚度分布图。

b. 由修正后的冰区重现期分布图可见，主要覆冰区分布在辽宁东部山区、辽宁南部沿海、辽宁西部及西南部沿海地区，这些地区主要受地形及水体分布的影响。

c. 在利用覆冰数据法开展冰区分级的同时，还对利用不同气象参数回归方法的覆冰分级方法进行了探讨。但基于目前的数据暂难以建立理想的数学回归模型。

［1］ 蔡文彪.500 kV输电线路覆冰舞动跳闸原因与对策 ［J］.东北电力技术，2009，30(12):35-37.

［2］ 赵永生，王富荣，赵德奎，等.电网覆冰事故分析及应对措施 ［J］.电工技术，2009，30(4):24-26.

［3］ 杨靖波，李 正，扬风利，等.2008年电网冰灾覆冰及倒塔特征分析［J］.电网与水利发电进展，2008，24(4):4-8.

［4］ 孙 羽，王秀丽.冰灾天气下输电网覆冰闪络跳闸风险评估［J］.东北电力技术，2013，34(9):1-4.

［5］ 郎振国，刘 良，徐宝臣.通辽地区输电线路发生覆冰舞动原因及对策 ［J］.东北电力技术，2006，27(11):19-22.

Study on Icing-region Ranking for Liaoning Electric Power System

SI Hong-dai1，ZHU Yi-dong2，HAN Hong-gang2，HAO Jian-cheng2
(1.Shenyang Institute of Engineering，shenyang，Liaoning 111036，China;2.Electric Power Research Institute of State Grid Liaoning Electric Power Co.，Ltd.，Shenyang，Liaoning 110006，China)

30-year data from all the icing observation stations in Liaoning are collected，which is reduced to the standard state of ice thickness，and the height and line diameter correction is made.Kriging interpolation method is used to get the ice thickness data covering the whole province.For the ice data of different areas，extreme value model is used to calculate ice thickness of different return period.Based on ice thickness data，icing-region ranking map for Liaoning electric power system is obtained for the first time.And also based on regression of different meteorological parameters，icing region ranking is discussed in this paper.

Icing data;Icing ranking;Extream model

TM75

A

1004-7913(2014)03-0009-04

book=13,ebook=307

司红代 (1961—)，男，学士，高级工程师，主要从事电力系统控制工作。

2013-12-10)