亚波长谐振腔实现方法研究

郭立娟

（长沙航空职业技术学院，湖南 长沙 410124）

0 引言

谐振腔是微波电路中一个不可或缺的器件。现代微波集成电路的发展要求减小器件尺寸，而传统谐振腔的工作波长与腔体尺寸相当。本文从Maxwell方程和边界条件出发，理论上分析了实现亚波长谐振的条件。电磁特异性介质材料（Metamaterials简称MTMs）[1]是指人工合成的具有自然介质材料所不具备的电磁特性的新材料。其中典型的为负折射率介质（NIM）又称为双负介质（DNG）、左手征材料（LHM）或者后向波媒质（BW）。早在1967年，前苏联理论物理学家Veselage在他的经典论文 Substances with Simultaneously Negative Values of ε and μ中提出了双负介质的概念[2]，但因为自然界找不到这样的材料而被搁置。直到上个世纪末英国皇家学院院士Pendry提出了分别实现负介电常数和负磁导率的人工电磁结构[3－4]，即MTMs的构造理论，并于2001年由加州大学圣迭戈分校物理系的Smith等在微波实验中首次实现[5]。从此MTMs获得了广泛的认可，相关的研究也蓬勃开展起来。根据理论分析，如将单负介质（介电常数和磁导率其中一个为负）或者双负介质（介电常数和磁导率同时为负）部分填充于谐振腔中，将出现谐振频率与谐振腔尺寸无关的谐振模式，即亚波长谐振模式[6－7]。亚波长谐振腔的实现对缩减微波集成电路尺寸，构造新型微波器件有着重要的价值。

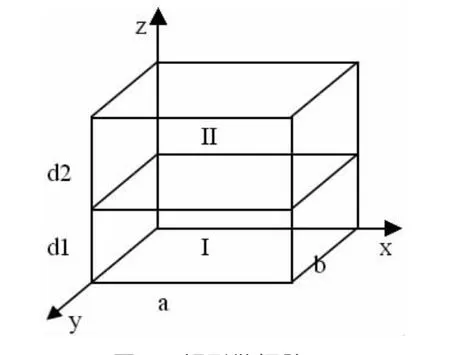
图1 矩形谐振腔

1 介质填充谐振腔的谐振本征方程

设一z向柱状谐振腔，xy平面内形状可以任意而不影响结论，为讨论方便，本文采用矩形。腔内沿z向分别填充两部分介质，如图1。对应I、II区域填充介质1和介质 2，厚度分别为d1、d2，电磁参数为 ε1、μ1；ε2、μ2。在假设腔内介质无耗、绝缘的情况下，根据 Maxwell方程组可以得到一组时谐Helholtz方程：

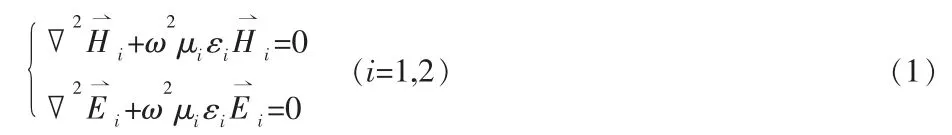
用分离变量法，先求出TE模和TM模的纵向分量，横向分量根据Maxwell旋度方程可以用纵向分量求出[8]。代入边界条件后得到TE和TM波对应的本征方程：

2 本征方程亚波长谐振模式解的讨论

简单的分析一下本征方程两边的函数性质我们可以得到这样的结论：两个填充区域介质的 ε1，ε2或者 μ1，μ2必须异号，相应的 TE 模、TM模本征方程才可能有解。由于tanh函数的单调性，本征方程满足亚波长条件的解只能有一个，以后我们用s下标来表示亚波长的某个模式，例如 TE10s、TM11s。

如确定了谐振腔的尺寸，本征方程（6）和（7）将在不同的介质填充条件下有不同的解。

（1）当 ε1=-ε2，μ1=-μ2时：

注意这里的εi，μi并没有规定符号，所以可能是电负媒质和磁负媒质，也可能是传统介质和双负介质。

则有lz1=lz2=lz，本征方程变为：

当且仅当d1=d2时lz有解，且lz可以为任意实数。由式（5）可知，此时任意频率均可谐振。

根据前面的本征方程有解条件可知此时只有TM模本征方程有解：

为方便讨论式（11）的解，令矩形波导a=b=d1+d2=1（cm），后面章节讨论时也采用这种尺寸的谐振腔，如无另外说明，所有长度单位均为厘米，且只讨论主模 TM11s模19.74×10-4。

图2所示为对应不同εr1的λ11S与d1关系曲线。图中由下至上εr1=1,1.2，…，2。

注意：为直观起见，横坐标使用的是谐振频率对应下的真空波长，单位为厘米。

b）ε1＞0，μ1＜0 即 I区填充磁单负介质

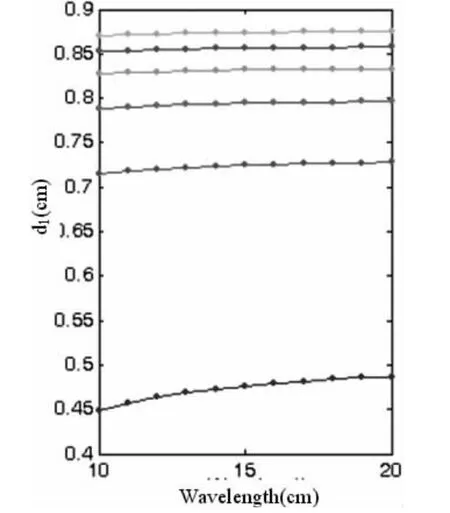
图2 λ11S与d1关系曲线随μr1变化图(由上至下 μr1=1,1.2，1.4，…，2)

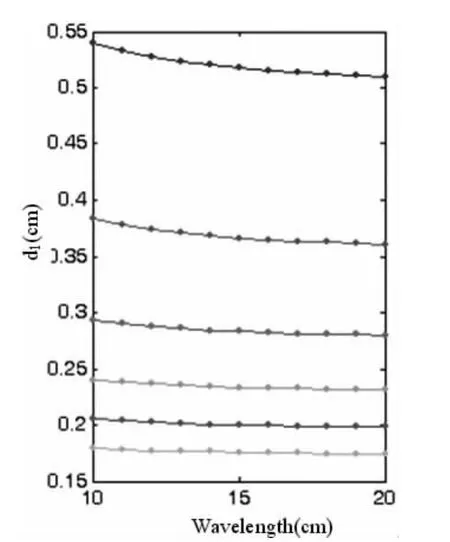
图3 λ11S与d1关系曲线随μr1变化图(由上至下 μr1=1,1.2，1.4，…，2)

注意：为直观起见，横坐标使用的是谐振频率对应下的真空波长，单位为厘米。

c）小结和推论

由a)和b)中的公式和数值模拟结果可知，使用单负媒质填充普通谐振腔可以实现亚波长谐振。填充的是磁负还是电负媒质，决定谐振模式是TE模还是TM模。改变填充比例可以得到不同的谐振波长。可以推论，如果在I区和II区分别填充电负和磁负媒质，也可以实现亚波长谐振，TE模和TM模均有解，且谐振波长主要与介质参数和填充比例相关。图4以II区真空I区填充电负介质为例给出了TM11S模在x=a/2 平面内的场型图。 计算时取 ε1=-1.2ε0，μ1=μ0，a=1m，d1=0.68m，d2=0.32m。

（3）εiμi＞0，ε1＜0，ε2＞0 即 I区填充双负介质，II区为传统介质；

此时，TE模和TM模本征方程均可能有解。

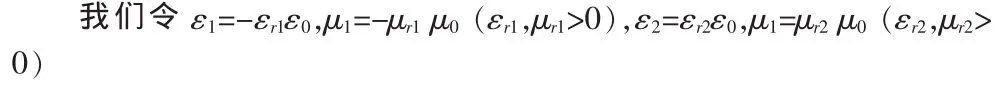
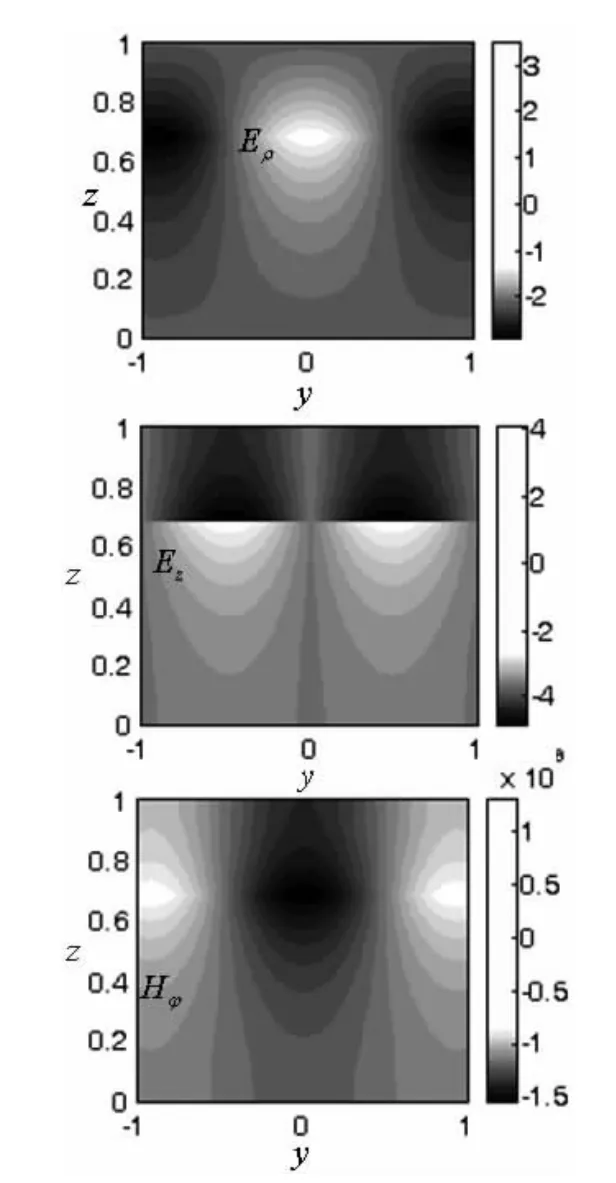
图4 TM11S模在x＝0平面内场型

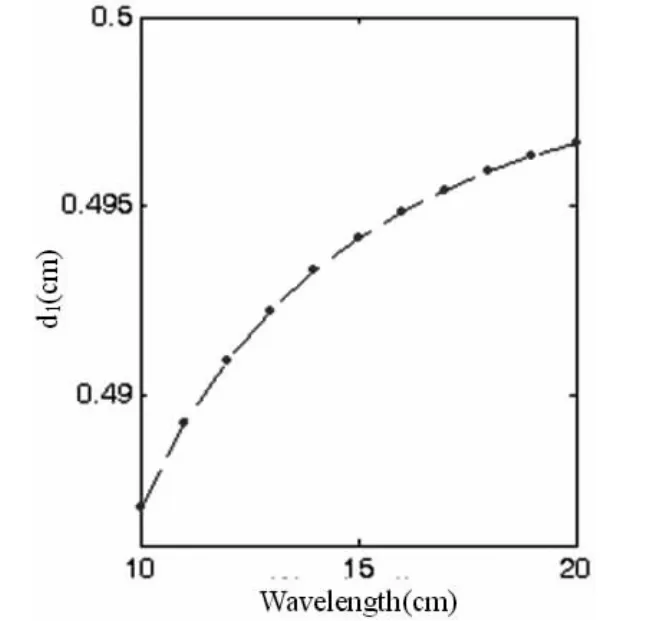
图5 λ10S与d1关系曲线

图6 λ11S与d1关系曲线

本征方程变为：

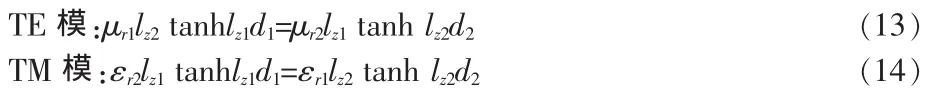
设 εr1=2，μr1=1，εr2=1，μr,2=1

图5为λ10S与d1关系曲线，图6为λ11S与d1关系曲线。可见，利用双负介质和传统介质同样可以实现亚波长谐振。

注意：为直观起见，横坐标使用的是谐振频率对应下的真空波长，单位为厘米。

3 亚波长谐振腔谐振波长的近似公式

假设谐振腔是立方体，a=b=d。我们以主模TE10s为例。

令：εi=εriε0，μi=μriμ0，d1=pa，d2=（1-p）a，p 为介质填充比例。

4 结束语

本文研究了亚波长谐振器的构造方法。研究表明，利用新型人工电磁介质进行部分填充，可以实现亚波长谐振腔，谐振波长主要与腔体内的填充介质和填充比例有关。本文的研究对于亚波长谐振腔的实现，缩减微波集成电路尺寸，构造新型微波器件十分有意义。

［1］Rokhesh S.Kshetrimayum,A brief intro to metamaterials[J].IEEE Potentials,Dec.2004/Jan.2005：44-46.

［2］V.G.Veselago,The electrodynamics of substances with simultaneously negative values ofand,Soviet Physics Uspekhi[J].Vol.10,No.4：509-514,January-February 1968.

［3］Pendry J B,Holden A J,Stewart W J,et al.Extremely low frequency plasmons in metallic mesostructures,[J].Phys.Rev.Lett,1996,(76),4 773-4776.

［4］Pendry J B,Holden A J,Robbins D J,et al.Magnetism from conductors and enhanced nonlinear phenomena,[J].IEEE Trans.Micr.Theory and Techniques,1999,(47)：2075～2084.

［5］Shelby R A,Smith D R,Schultz S.Experimental verification of a negative index of refraction,[J].Science,2001,(292)：77-79.

［6］Silvio Hrabar,Juraj Bartolic,Zvonimir Sipus,Waveguide miniaturization using uniaxial negative permeability metamaterial[J].IEEE TRANSACTIONS ON ANTENNAS AND PROPAGATION,VOL.53,NO.1,JANUARY 2005：110-119

［7］Nader Engheta,An idea for thin subwavelength cavity resonators using metamaterials with negative permittivity and permeability,IEEE ANTENNAS AND WIRELESS PROPAGATION LETTERS,VOL.1,2002：10-13.

［8］R.F.Harrington,Time-harmonic electromagnetic fields[M].McGraw-Hill Book Co.1961.