一题多解探讨二重极限的计算
2014-04-22徐泰燕
徐泰燕
(武昌工学院,湖北 武汉 430065)
二元函数为代表的多元函数的极限定义和一元函数的极限定义均可利用“ε-δ定义[1]”给出,表面上看,多元函数的重极限的复杂度只是由于变元个数的增加引起的,但实际上,相比一元函数在x0处的点极限仅要求x从x0的左、右两侧直线趋近于x0不同,多元函数的重极限对趋近路径有更高的要求,即满足任意性(既包括沿两个坐标轴方向的直线路径,也包括更复杂的任意函数曲线路径),因此,二元函数的极限求解问题相对复杂很多。
但有时题目不满足相应的条件,无法运用相应的方法,例如在实际教学过程中遇到的下面求二重极限在点(0,0)处无意义,进而不连续,从而本极限不能利用二元函数的连续性计算该极限,但可以结合相关二元函数的理论探讨其他求解方法。本文针对该题给出五种不同的解答方法,以供大家教学时参考。
求一元函数的极限有许多方法,如:四则运算求极限法、等价无穷小量代换法、有界量乘以无穷小量仍为无穷小量的结论、两类重要极限、利用连续性、洛必达法则等,上述方法在条件满足的情况下可以推广到二元函数为代表的多元函数的重积分计算中,也即重积分的计算可以选择恰当的变量代换转化成一元函数的极限求解,进而使问题变得简便。
在一元函数的极限求解中,当x→0时,sinx→0和ln(1+x)均为无穷小量,利用第一类重要极限可知 sinx~x,同理,ln(1+x)~x,在做极限的乘除法运算时,可将sinx用x代换,ln(1+x)用x代换,从而=1,可见恰当的进行等价无穷小代换可使极限问题变得简便。 而对于本题,当(x,y)→(0,0)时,sin(x3+y3)→0,可令 x3+y3=u,类似于一元函数的等价无穷小代换理论将sinu用u代换,即将方法进行探讨,以下不再对此再做一一单独说明。
1 先猜测极限,再用二重极限的“ε-δ定义”证明结论
极限的“ε-δ定义[1]: 设函数 z=f(x,y)的定义域为 D,P0(x0,y0)是 D的聚点,如果存在常数A,对于任意给定的正数ε(无论多么小),总存在正数 δ,使得当点 P(x,y)∈D∩ (P0,δ)总有<ε 成立,则称 A 为函数 z=f(x,y)当(x,y)→(x0,y0)(或 P→P0)时的极限,记作x,y)=A。
给定∀ε>0(无论多么小),利用放缩法,要使下面式子
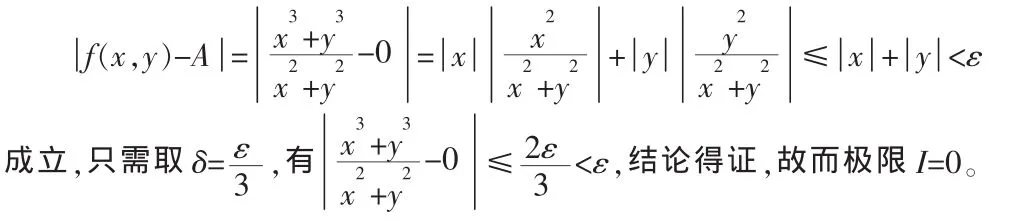
2 利用一元函数极限的 “有界量乘以无穷小量仍为无穷小量”结论求解
对于一元函数的极限,有下面定理:
定理1[1]在某一极限过程中,若 α(x)是无穷小量,f(x)是有界函数,则 α(x)f(x)仍是无穷小量。
对于上面定理,可将其推广到多元函数的重极限计算中,本例中,对函数做变形得:
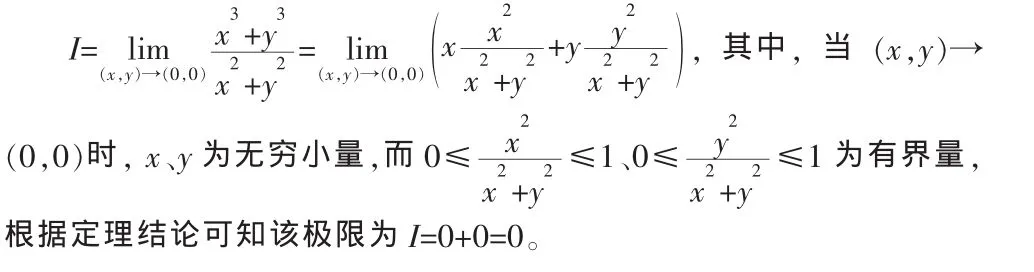
3 利用解析函数的L’Hospital法则求解
定理 2[2]设 f(z)=u(x,y)+iv(x,y),g(z)=w(x,y)+ih(x,y)是以 z0=x0+y0为零点的两个不恒等于0的解析函数,则有:

4 利用极坐标变换计算
在二重极限的计算中,当出现(x,y)→(0,0),且二元函数解析式中包含x2+y2的形式时,一般可考虑极坐标变换法。
利用上面结论,在本例中,x0=0,y0=0,可令 x=rcosθ,y=rsinθ,

5 利用二元函数的洛必达法则求解
定理 3[4]若二元函数 f(x,y)、g(x,y)满足:(1)在

6 结论
[1]黄立宏.高等数学[M].复旦大学出版社,2010.
[2]倪培溉.用L’Hospital法则求解某些二元函数的极限[J].中国民航学院学报,2003(7):6-7.
[3]沈彩霞.二元函数极限的计算[J].河池师专学报,2002(6):42-43.
[4]张立新.二元函数的微分中值定理及罗比达法则[J].辽宁教育学院学报,2001(9):21.
