分片铺设压电梁弯曲分析的无网格法
2014-04-21袁学帅
袁学帅
(内蒙古民族大学数学学院,内蒙古通辽028043)
分片铺设压电梁弯曲分析的无网格法
袁学帅
(内蒙古民族大学数学学院,内蒙古通辽028043)
由不同材料层合而成的层合压电结构中,各层之间的材料的不连续性使得采用无网格配点法处理此类问题时的精度降低.为解决这一问题,将整个问题区域根据材料属性划分成不同的子区域,在每个子区域内采用无网格配点法.为实现各子区域的“粘合”,在子区域的公共边界上分别施加力、电相容性条件和位移、电势连续性条件,导出子区域下的无网格配点法;并应用该方法对层合压电结构在不同铺设方式下的弯曲进行分析并比较.结果表明:分片铺设压电片时,对同样体积大小的压电材料,不同的压电布置会产生不同的对形变的控制效果;采用上下对称粘贴的的铺设方式能实现较好的控制效果.
层合梁;压电;分片铺设;配点法
0 引言
压电材料是一种智能材料,当压电晶体受外力作用发生形变时,在它的表面上出现异号极化电荷,从而形成电场;同样地,当对压电晶体施加一电场时,由极化电荷作用而产生应变和应力.基于上述特点,压电材料成为智能结构传感器、驱动器的首选材料.由于压电材料的力电耦合性,使解析求解压电结构问题时非常困难,故寻求合理的数值方法对于求解压电问题具有重要意义.
目前,利用无网格法在压电结构力学分析取得了一定的成果.Liu等[1]采用基于径向基函数插值的方法处理层合压电结构的静态挠度问题,Liew等[2]用无单元伽辽金方法在力电的共同作用下分析复合梁、板,上述都是基于弱式的方法. Chen等[3]采用局部径向基配点法,解决了由不同材料层合而成的板、梁在力的作用下的应力应变问题.然而,类似的思想却很少用在压电层合材料问题中.
基于径向基函数近似的配点法具有实现简单和指数收敛性等优点[4],然而在处理力电耦合的压电层合结构时,由于各层之间的材料属性不同而破坏了材料之间的连续性,光滑和全局的径向基函数在解决这类问题时所得到的数值解往往精确度不高、稳定性差.基于上述缺点,可对整个求解域根据不同材料属性划分成相应的子区域,在子区域内采用无网格配点法,然后在子区域的公共边界分别施加位移、电势连续性条件和力、电相容性条件.这样就使不同材料之间“粘合”起来,最后组装总刚度矩阵,得出了求解层合压电结构的子区域配点法,并已验证此方法增强了数值解的精确性和稳定性.本文继续应用该方法,在不同的铺设方式、铺设位置下,分析压电结构的弯曲效果.
1 径向基函数近似
考虑二维区域Ω内的一个场函数w(x),首先对整个区域进行离散.xQ为区域内计算点,其支撑域内有n个节点xi(i=1,2,…,n),可插值得到场函数w(x)在支撑域中的近似函数[5]

Ri(x)是关于x、xi的距离ri的径向基函数,Pj(x)为多项式基函数.多项式基的个数取决于对重构的要求,一般来说,二维线性基取

二维二次基取

其中ai,bj为待定系数,通过支撑域内的n个节点的插值确定.使式(1)满足计算点x周围n个节点xi(i=1,2,…,n)的值,将得到n个线性方程:

然而,方程组(2)具有n个方程,未知数的个数却有n+m个,因此可加入限制条件[6]
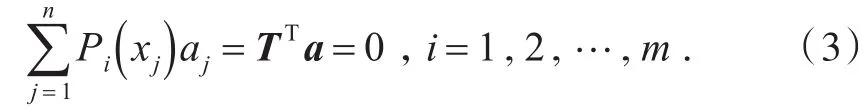
联立(2)、(3),可得到


将式(5)代入式(1),得到


式中φi(i=1,2,…,n)为Φ(x)的分量.
2 压电层合材料方程
2.1 子区域划分
在层合压电问题中,不同的材料有不同的材料属性,各微分算子在不同的材料中会有很大差异.若将压电结构作为整体考虑会引起计算精度的降低.基于此类问题,可将不同的压电材料分区域处理.为简便起见,以两个区域为例.考虑区域Ω(边界为∂Ω)由两个不同的开区域Ω1和Ω2组成,其边界分别为∂Ω1,∂Ω2,公共边界为S12,(如图1所示).定义闭区域:设位移、应力、电势、电位移边界分别为Su,St,Sϕ,Sω,则St∪Su= Sω∪Sϕ=∂Ω,St∩Su=Sω∩Sϕ=null.
2.2 压电控制方程
考虑平面压电问题,假设无外载电荷,极化方向沿厚度(Z轴)方向,在XZ平面下建立压电控制方程[7].在上述两个子区域组成的问题域中,每个子区域内均为连续的.因此在各子区域均满足力电耦合平衡方程、几何方程及本构方程,如式(8)~(10)所示.
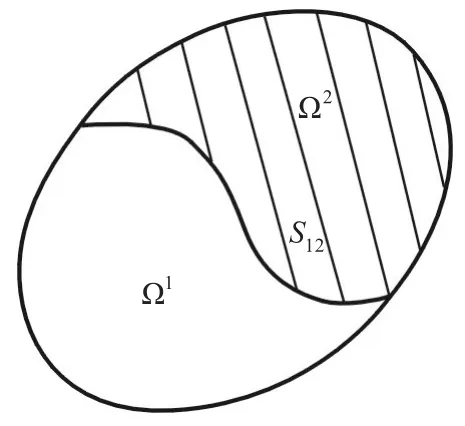
图1 不同材料的子区域Fig.1 Two sub-domain of a problem w ithmaterial heterogeneity
力-电耦合平衡方程
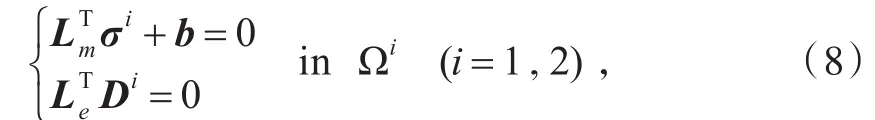
几何方程

力-电耦合的本构方程
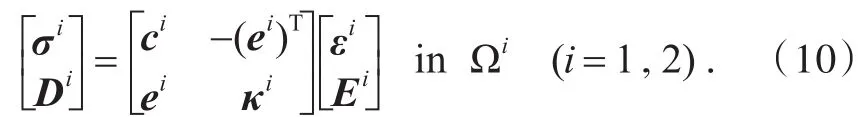
电场强度与电势的关系

其中,Lm,Le为微分算子,σ、ε分别为应力和应变向量,E、D、ϕ分别表示电场强度、电位移和电势.
边界条件及连续性条件阐述如下,
a.自然边界条件

b.本质边界条件

对于一般弹性体,我们可考虑其位移、电势的连续性和面力均衡的原则,且已证明同时考虑这两个原则收敛效果更好[3].因此,公共边界的条件可表示为:
其中,qis表示为电荷面密度边界上的给定面
电荷密度,t
i
表示力的自然边界上给定的力,
,
分别为力、电本质边界上给定的位移和电势.n
m
为力边界的法向分量,n
e
为电边界的法向分量.
由(8)~(13)可得相应的子区域力-电耦合问题的基本方程为


对力-电耦合问题可施加(14)~(17)式所示的四个边界条件,简单表示为:

3 配点法的实现
设以下符号i=1,2表示不同介质,用配点法对求解域进行离散.Npi为区域Ωi中的节点数;自然边界Sti上的节点数记为Nti;本质边界Sui上的节点数为Nui;NS是公共边界S12上的节点数.每个区域上的总结点数即为在每个子区域中,其场函数(u,w,ϕ)可由此区域中的形函数插值近似(6)式得到:
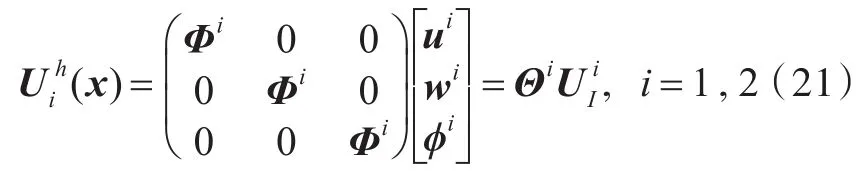
其中,Φi、UiI分别为第i个区域的形函数向量和广义节点位移向量.将(21)式代入(18)式可得到:

4 分片铺设压电结构的弯曲分析
图2为分片铺设情况示意图.考虑图2所示的分片铺设压电悬臂梁,对图中不同铺设情况下压电悬臂梁的弯曲进行分析.基体层是厚度较大的无极化性质的AS/3501 Gr/ep基体,基体长度为100 mm,厚度为10 mm.压电材料为PZT G-1195N,极化方向沿厚度方向.3种情况下压电片的厚度均为1 mm.图2中(a)压电片长度为60 mm,(b)、(c)中压电片的长度均为(a)中的一半.(b)中两压电片上下对称铺设,粘在基体表面,施加相反方向的电压;(c)中两压电片也为上下对称铺设,但其内嵌到基体里面,表面和基体水平,同样施以相反方向的电压[8].其材料属性见表1.

图2 分片铺设情况Fig.2 Situationsof distributed piezoelectric patches

表1 材料属性Table 1 Material property
首先对同样体积大小的压电材料,施加相同的电压,考虑不同的铺设方式对压电悬臂梁的弯曲程度的影响.设压电片左端到梁左边界的距离为l(mm),3种情况下均取l=20,施加电压均为100 V.图2(a)方式将基体和压电片分成两个子区域,基体均分成51×6个数据点,压电片均分成31×2个数据点,图2(b)、(c)均将基体和压电片分成3个子区域,上下压电片均分成16×2个数据点,图2(b)中基体均分成51×6个数据点,图2(c)中基体均分成51×7个数据点.在子区域内采用无网格配点法,子域的交界面上分别施加位移、电势连续性条件和力、电相容性条件,得到基体中轴线的弯曲情况如图3所示.可以看出,3种铺设方式下分析比较由压电片产生的基体中轴线的挠度,采用图3(b)、图3(c)方式铺设的效果均比图3(a)显著;采用图3(c)方式铺设时,执行器末端的挠度较大,对基体的变形影响较大;采用图3(b)方式铺设时,梁的挠度曲线较为光滑,弯曲效果较好,故能实现比较好的控制效果.
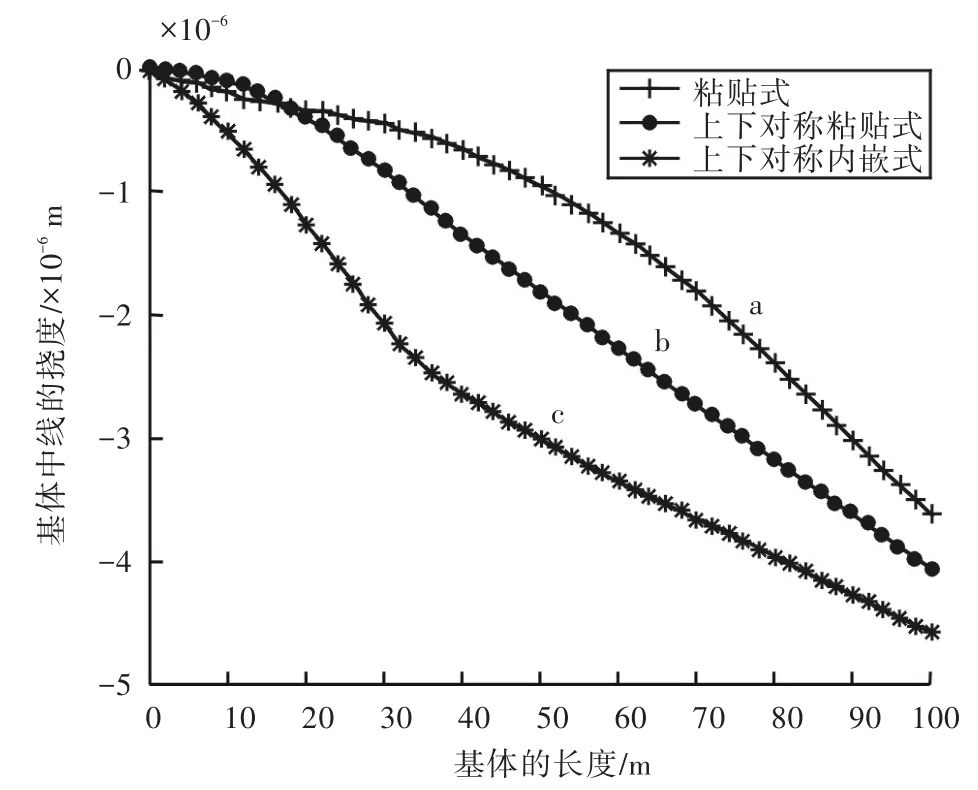
图3 不同铺设方式下基体中轴线的弯曲情况Fig.3 The bending ofmatrix axes for different distributed ways
然后分别取(l=2,6,10,14,18,22),在3种铺设方式下,分析压电片的不同位置对梁端点的挠度的影响,见表2.可以看出,同种电压下,压电片自基体左端向右移动时,产生的端点挠度逐渐增大.且采用图3(b),图3(c)方式铺设时,执行器末端的挠度增长较快,控制效果显著.

表2 相同电压下(100 V)压电片的铺设模式和位置对端点挠度的影响Table 2 Theend pointdeflection of piezoelectric patchesof layingmodeand the location under the same voltage(100 V)
5 结语
本文根据层合压电结构的不同材料属性,将求解域划分成相应的子区域,在子区域上应用基于径向基函数的无网格配点法,并在子区域的公共边界上分别施加位移、电势连续性条件和力、电相容性条件.最后组装总刚度矩阵,得出了求解层合压电结构的子区域配点法,并应用于层合压电结构中.通过数值算例结果表明,分片铺设压电片时,对同样体积大小的压电材料,不同的压电布置会产生不同的对形变的控制效果.采用上下对称粘贴式铺设时,能达到比较好的控制效果.此方法可进一步应用到分片铺设的压电层合板结构中.
致谢
感谢苏州大学姚林泉教授对论文撰写中提出的重要修改和建议.
[1]Liu G R,Dai K L,Lim K M,et al.A radial point interpolation method for simulation of two-dimensional piezoelectric structures[J].Smart M ater Struct,2003,12:171-180.
[2]Liew K M,Lim H K,Tan M J,et al.Analysis of lam inated com posite beam s and plates with piezoelectric patches using theel element-free Galerkin method[J].Com put M ech,2002,29:486-497.
[3]Chen JS,Wang L H,Hu H Y,et al.Subdomain radial basis collocation method for heterogeneous media[J]. International Journal for Numerical M ethods in Engineering,2009,80(2):163-190.
[4]Sharan M,Kansa E J,Gupta S.Applications of the multiquadric method for the solution of elliptic partial differential equations[J].Appl M ath Com put,1997,84:275-302.
[5]Nayroles B,Touzot G,Villon P.Generalizing the finite element method:diffuse approximation and diffuse elements[J].Comput Mech,1992,10(5):307-318.
[6]Liu G R.M esh free methods:Moving beyond finite elementmethod[M].Boca Raton:CRC Press LLC,2002.
[7]袁学帅,陈富军,姚林泉.压电层合结构的子域配点法[C]//2010全国压电和声波理论及器件技术研讨会,2010,441-446.
YUAN Xue-shuai,CHEN Fu-jun,YAO Lin-quan. Subdomain collocation method for multilayered piezoelectric material[C]//Proceedings of the 2010 Sym posium on Piezoelectricity,Acoustic Waves and Device Applications,2010,441-446.(in Chinese)
[8]姚林泉,俞焕然.具有压电材料薄板稳定性的有限元法[J].兰州大学学报,1999,35(1):44-48.
YAO Lin-quan,YU Huan-ran.Finite elementmethod of stability for thin plate of piezoelectric material[J]. Journal of Lanzhou University,1999,35(1):44-48.(in Chinese)
Analysis of piezoelectric beam with distributed patches using meshless method
YUAN Xue-shuai
(School of Mathematical,Inner Mongolia University for Nationalities,Tongliao 028043,China)
To improve the accuracy of meshless method for multilayered piezoelectric,the domain withproblem was divided into some sub-domains using point collocation method according to the materialproperties. On the interface of each sub-domain,the conditions of mechanical and electric reciprocity,displacement and electric potential continuity are imposed,which can be used to glue the two neighboringsub-domain solutions together. Then,a sub-domain point collocation method was presented to solve themultilayered piezoelectric problem and analyze the bending of piezoelectric patches distributed in differentways. The results show that different piezoelectric arrangements have different effects on deformation for thesame size of piezoelectric materials,and using the vertically symmetrical pasting can achieve better controleffect compared with the other ways.
multilayered beam;piezoelectric;distributed piezoelectric patches;point collocation method
O24
A
10.3969/j.issn.1674-2869.2014.01.015
1674-2869(2014)01-0074-05
本文编辑:龚晓宁
2013-10-25
袁学帅(1986-),男,山东济宁人,助教,硕士.研究方向:计算数学和计算力学.
