二元恒残液组成提馏式间歇精馏的捷算法
2014-04-21王为国段晓玲曾真王存文吴元欣
王为国,段晓玲,曾真,王存文,吴元欣
[1.武汉工程大学化工与制药学院,湖北武汉430074;2.绿色化工过程教育部重点实验室(武汉工程大学),湖北武汉430074;3.武汉工程大学机电工程学院,湖北武汉430074]
二元恒残液组成提馏式间歇精馏的捷算法
王为国1,段晓玲2,曾真3,王存文2,吴元欣2
[1.武汉工程大学化工与制药学院,湖北武汉430074;2.绿色化工过程教育部重点实验室(武汉工程大学),湖北武汉430074;3.武汉工程大学机电工程学院,湖北武汉430074]
探讨了二元恒残液组成提馏式间歇精馏在理想操作条件下汽化总量的数值计算方法.采用数值计算方法计算出二元恒残液组成提馏式间歇精馏,给定分离任务理论板数与汽化总量的对应关系,并通过关联计算结果得到其理论板数与汽化总量的近似关系式.对于给定的分离任务,如果已知汽化总量,用该近似关系式计算理论板数与精确解的最大正相对偏差为0.027 1,最大负相对偏差为-0.028 8,平均相对偏差为0.014 6;如果已知理论板数,用该近似关系式计算汽化总量与精确解的最大正相对偏差为0.041 8,最大负相对偏差为-0.035 1,平均相对偏差为0.016 5.因此,该近似关系式具有很好的计算精度.
间歇精馏;恒残液组成;提馏式;捷算法
0 引言
间歇精馏提馏式操作方式最早由Robinson和Gilliland[1]于1950年提出,其流程与操作方式见文献[2].Chiotti[3-4]等、Sørensen[5]等研究均得到,当原料中轻组分含量很低的时,较常规间歇精馏,提馏式操作方式能耗相对较低的结论.许松林等[6-7]研究了提馏式间歇精馏塔的设计方法及控制方法.张雪梅[7]等推导了二元恒再沸比提馏式间歇精馏过程的最小再沸比计算方法.笔者[9-10]分别对二元常规间歇精馏恒馏出液组成操作方法的理论板与再沸器汽化总量、恒回流比操作方法的理论板与回流比进行了关联,得到相应的捷算法.近来笔者[2]推导出二元恒残液组成提馏式间歇精馏,理想操作条件下最小汽化总量的计算公式,为其捷算法提出提供可能.本研究通过对二元恒残液组成提馏式间歇精馏的理论板与塔釜汽化总量进行关联,得到其捷算法.
1 再沸器汽化总量的数值计算方法
二元恒残液组成提馏式间歇精馏的流程见文献[2]图1.操作条件同文献[2],本研究称之为理想操作条件.基本方程见文献[2]式(1)~(8),式(20)~(23).理想操作条件下二元恒残液组成提馏式间歇精馏,在对塔顶贮槽内液体中轻组分浓度由xF变为xDe的精馏过程离散后,可用试差图解法求解出给定的分离任务理论板数与汽化总量的对应关系,但因其计算量非常大,用试差图解法大规模的计算几乎不可能.以下简要介绍用图解法原理,编程计算的方法.本研究所介绍的数值计算方法,主要满足本文关联N+1与nV的需要,其步骤及相关的(离散化)方程如下:
①输入:α、nF、xF、xW、ηh、N+1和k.
②计算xDe.
由文献[2]式(8)、(2)、(3)得

③i=0.
④确定x(i)D.

⑤计算R(i)b.
计算R(i)b的过程较为复杂,后文将详细说明.
⑥判断i+1>k是否成立.
如果不成立,i=i+1,转到④
如果成立,计算nV,输出计算结果.
由文献[2]式(23)得

上述计算过程步骤⑤是计算已知α、xD、xW和N+1时的Rb,具体过程(见图1示意,作图1的条件为:α=2.5、xD=0.50、xW=0.10、N+1=6,试差作出的操作线为-ba,此时,y1=0.68, Rb=2.22.)为:假定Rb的数值,从xW开始,交替使用文献[2]式(1)与式(4)(即:逐板计算法)计算出x0.如果x0>xD表明假定Rb的数值过大(图中的线-ba"所示).如果x0<xD表明假定Rb的数值过小(图中的线-ba'所示).如果x0=xD,表明假定Rb的数值就是所要求的(如:图中的线-ba所示).由图1可见,对于正常的精馏过程,当α、N+1和xW一定时,x0是Rb单调增函数,因此,数值法计算已知α、xD、xW和N+1时的Rb较为合理方法为:采用Newton法修正Rb迭代求解.

图1 Rb求解示意图Fig.1 schematic diagram of solving Rb
2 最少理论板数
二元恒残液组成提馏式间歇精馏过程中,再沸器汽化速率V为有限值,只有在塔底出料液速率W→0时,才有Rb=V W→∞.当Rb=V W→∞时,N+1→Nm+1.由塔顶贮槽内液体中轻组分浓度由xF变为xDe的精馏过程中,xW不变,xD在增大,所需的最少理论板数是变化的,瞬时最少理论板数由芬斯克方程得

精馏起始时,所需的最少理论板数最小为

精馏终了时,所需的最少理论板数最大为
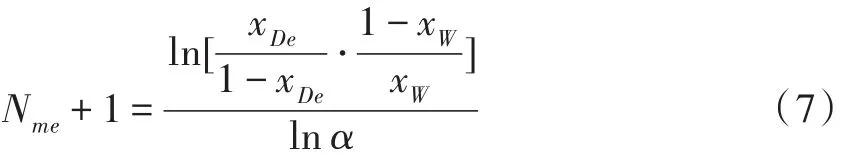
3 最小汽化总量
二元恒残液组成提馏式间歇精馏,当N+1→∞时,nV→nVm.塔顶贮槽内液体中轻组分浓度由xF变为xDe的精馏过程中,塔釜汽化总量用下式计算,见文献[2]式(25).

4 捷算法
获得二元恒残液组成提馏式间歇精馏N+1与nV复杂对应关系的近似计算式的具体步骤如下:
(1)确定分离任务对在理想操作条件下,确定二元理想混合物间歇精馏分离任务的4个独立变量(α,xF,xW,ηh)用5水平正交设计方案取值给定25个分离任务(见表1).
(2)由式(8)计算的各分离任务的nVm/nF.
(3)由式(6)、(7)计算的各分离任务的Nms+1、Nme+1.
(4)按N+1≈(1.3~1.5)(Nme+1)整数,选定各分离任务的N+1,用数值计算法计算对应的nV/nF.
(5)关联.对对应的数据进行变量组合,令
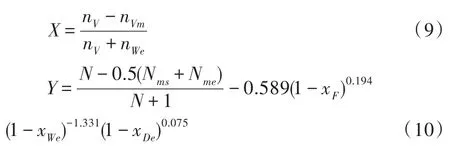
关联对应的X与Y得

由表1、图2可见,式(11)很好地表达了Y与
X的近似关系,如果已知X,用式(11)计算Ya与精确解的最大正偏差(Y-Ya)为0.018 1[见表(1)编号3分离任务],最大负偏差为-0.015 9[见表(1)编号21分离任务],平均偏差0.008 4.对于给定的分离任务,如果已知nVnF,用式(11)计算Na+1与精确解的最大正相对偏差[(Na-N)(N+1)]为0.027 1[见表(1)编号21分离任务],最大负相对偏差为-0.028 8[见表(1)编号3分离任务],平均相对偏差为0.014 6(见图3);如果已知N+1,用式(11)计算nVa与精确解的最大正相对偏差[(nVa-nV)nV]为0.041 8[见表(1)编号21分离任务],最大负相对偏差为-0.035 1[见表(1)编号3分离任务],平均相对偏差为0.016 5(见图4).此外,必须说明的是,关联出式(11)中N+1的取值范围为N+1≈(1.3~1.5)(Nme+1),应用式(11)计算,如果N+1的值过大(或过小),均可能引起较大的偏差.

表1 N+1和nV的关联数据表Table 1 Data of correlation N+1 w ith nV

图2 Y(Ya)和X的关系Fig.2 Relationship of Y(Ya)and X

图3 Na+1和N+1的偏差Fig.3 Deviation of Na+1 from N+1

图4 nVanF和nVnF的偏差Fig.4 Deviation of nVanFfrom nVnF
5 结语
a.介绍了二元恒残液组成提馏式间歇精馏,理想操作条件下,汽化总量的数值计算方法.
b.关联了恒残液组成二元提馏式间歇精馏时,给定的分离任务的理论板数与汽化总量,得其近似关系式(式(11)),该近似关系式具有很好的计算精度.
符号说明
Nm+1——瞬时最少理论板数(包括塔釜);
Nms+1——精馏起始时的最少理论板数(包括塔釜);
Nme+1——精馏终了时的最少理论板数(包括塔釜);
nF——原料量,kmol;
nDe——塔顶产品量,kmol;
nV——再沸器汽化总量,kmol;
nVm——再沸器最小汽化总量,kmol;
nWe——塔底产品量,kmol;
Rb——再沸比;
V——塔内汽相流率,kmol·h-1;
W——塔底出料液速率,kmol·h-1;
x——塔板上轻组分的摩尔分数;
xD——塔顶贮槽中轻组分的瞬时摩尔分数;
xF——原料中轻组分的摩尔分数;
xW——塔底出料中轻组分的摩尔分数;
α——相对挥发度;
ηh——塔底产品中重组分的收率;
上角标
a——近似计算结果;
(i)——数值计算时,各物理量第(i)段对应的数值.
致谢
感谢武汉工程大学化工与制药学院提供的实验平台.
[1]Robinson C S,Gilliland E R.Elements of fractional Distillation[M].4th ed.New York:M cGraw-Hill,1950.
[2]王为国,曾真,覃远航,等.恒再沸比提馏式间歇精馏的最小再沸流比与能耗分析[J].化工学报,2012,63(7):2106-2112.
WANGWei-guo,ZENG Zhen,QIN Yuan-hang,etal. Energy consumption analysis and m inimum reboil ratio of stripping batch distillation under constant reboil ratio[J].Journal of Chem ical Industry and Engineering,2012,63(7):2106-2112.(in Chinese)
[3]Chiotti O J,Iribarren O A.Simplified models for binary batch distillation[J].Computers&Chem ical Engineering,1991,15(1):1-5.
[4]Chiotti O J,Salomone H E,Iribarren O A.Selection of multicomponent batch distillation sequences[J]. Chem ical Engineering Communications 1993,119(1):1-21.
[5]Sørensen E,Skogestad S.Com parison of regular and inverted batch distillation[J].Chem icalEngineering Science,1996,51(22):4949-4952.
[6]XU Song-lin,Salomone H E,Iribarren O A.Shortcut procedure for inverted batch distillation column(I)multicom ponent ideal system[J].Chinese Journal of Chem ical Engineering,2001,9(1):28-33.
[7]Xu S L,Espinosa J,Salomone H E,et al.Operation of a batch stripping distillation column[J].Chinese Journal of Chem ical Engineering,2001,9(2):141-144.
[8]张雪梅,郭锦棠,张卫江.二元物系提馏式分批精馏过程[J].大津大学学报,2005,38(11):950-954.
ZHANG Xue-mei,GUO Jin-tang,ZHANG Wei-jian.Binary Stripping Batch Distillation[J].Journal of Tianjin University,2005,38(11):950-954.(in Chinese)
[9]王为国,曾真,张所信,等.二元混合物恒馏出液组成间歇精馏的捷算法[J].武汉化工学院学报,1999,21(3):5-9.
WANGWei-guo,ZENG Zhen,ZHANG Suo-xin,et al. Shortcut method for batch distillation of binary m ixture under constant distillate com position[J]. Journal of Wuhan Institute of Chem ical Technology,1999,21(3):5-9.(in Chinese)
[10]王为国,曾真,毕亚凡,等.二元混合物恒回流比间歇精馏的捷算法[J].武汉化工学院学报,2000,22(1):16-19.
WANG Wei-guo,ZENG Zhen,BI Ya-fan,et al. Shortcut method for batch distillation of binary m ixture under constant reflex ratio[J].Journal of Wuhan Institute of Chem ical Technology,2000,22(1):16-19.(in Chinese)
Shortcut method of binary stripping batch distillation under constantresidual fraction composition
WANG Wei-guo1,DUAN Xiao-ling2,ZENG Zhen3,WANG Cun-wen2,WU Yuan-xin2
[1.School of Chemical Engineering and Pharmacy,Wuhan Institute of Technology,Wuhan 430074,China;2. Key Laboratory for Green Chemical Process of Ministry of Education(Wuhan Institute of Technology),Wuhan 430074,China;3.School of Mechanical and Electrical Engineering,Wuhan Institute of Technology,Wuhan 430074,China]
The numerical method for calculating total vapor capacity of binary stripping batch distillationunder constant residual fraction composition and ideal operation conditions was explored. The correspondingrelationship between the theoretical trays and the total vapor capacity of binary stripping batch distillationunder constant residual fraction composition was figured out by the numerical method for given separationtasks,and an approximate relationship between the theoretical trays and the total vapor capacity was set upthrough correlating the calculated results. For a given separation task,if the total vapor capacity was known,the maximum positive relative deviation and the maximum negative relative deviation between the calculatedtheoretical trays based on the approximate relationship and the exact solution were 0.027 1 and -0.028 8,respectively,and the average relative deviation was 0.014 6. If the theoretical trays were known,themaximum positive relative deviation and the maximum negative relative deviation between the calculatedtheoretical trays based on the approximate relationship and the exact solution were 0.041 8 and -0.035 1,respectively,and the average relative deviation was 0.016 5. Therefore,the approximate relationship has agood calculation accuracy.
batch distillation;constant residual fraction composition;stripping;shortcut method
TQ015
A
10.3969/j.issn.1674-2869.2014.01.003
1674-2869(2014)01-0009-05
本文编辑:张瑞
2013-06-03
王为国(1963-),男,江苏建湖人,副教授,硕士.研究方向:间歇精馏基础理论.
