浅析工业机器人的坐标转换矩阵算法
2014-04-20殷卓
殷 卓
(北京光电技术研究所,北京, 10010)
浅析工业机器人的坐标转换矩阵算法
殷 卓
(北京光电技术研究所,北京, 10010)
本文主要阐述笔者在使用史陶比尔六轴工业机器人进行激光加工的过程中总结出的一种计算方法,该方法基于线性代数理论对机器人的关节坐标和笛卡尔坐标进行相互转换。这种方法易于理解,既不要求机器人编程者掌握高深的数学知识,也不要求编程者购买价格昂贵的机器人模拟软件,可以实现六轴工业机器人位置的笛卡尔坐标与关节坐标的相互转换求解。通过实例验证,用此方法计算出的机器人关节坐标值,和史陶比尔机器人得出的关节坐标值相差在千分之一以内。
工业机器人,坐标转换
0 概述
工业机器人是面向工业领域的多关节机械手。关节坐标系和世界坐标系是工业机器人的两个基本坐标系,两者之间相互转换的算法是机器人算法的基础。各机器人厂家有各自的算法,但不会向使用者详细介绍,所以机器人使用者往往不易更加深入了解机器人的内部算法,这在某种程度上对机器人的编程使用造成了一定的难度。本文浅显地论述了一种矩阵算法,可以加深机器人使用者对机器人工作原理的理解,对其在进行机器人编程、选型购买、方案设计等工作时起到一定的帮助作用。此方法获得的结果与实际机器人自身的运行结果高度吻合,验证了此方法的正确性。
1 机器人坐标系
1.1 关节坐标系
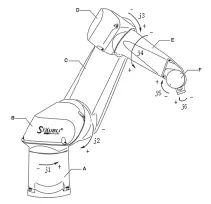
图1 关节坐标系
关节坐标是工业机器人最基本的坐标系。如图1所示的工业机器人具有六个自由度,j1,j2,j3,j4,j5,j6这六个自由度给定六个关节的角度值(单位为°,旋转方向如图1中箭头方向所示)。习惯上将这六个自由度叫作机器人的六个轴。
1.2 世界坐标系
世界坐标系如图2所示,是一种笛卡尔坐标系,它类似于一般数控机床的机床坐标系。它包括原点和符合右手定则的XYZ三个坐标轴。其中,原点是机器人底座的中心点,X轴正向指向机器人的正前方,Z轴指向机器人的正上方,Y轴由右手定则规定,即指向如图2所示的右方。世界坐标系同样具有六个自由度。这六个自由度包括三个位置x,y,z和三个角rx,ry,rz。在机器人尚未夹持工具的情况下,x,y,z代表第六轴法兰盘圆心相对于原点的位置偏移量。rx,ry,rz代表第六轴法兰盘的轴线角度,由初始姿态即竖直向上绕z轴旋转rz度,再绕y轴旋转ry度,再绕x轴旋转rx度得到。
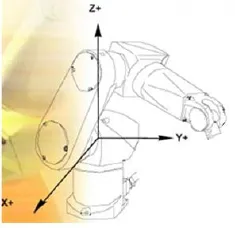
图2 世界坐标系
1.3 工具坐标系

图3 机器人第六轴法兰盘
工具坐标系类似于数控机床的刀补。首先,在机器人尚未夹持工具(如焊枪、油漆喷头等)的时候,机器人默认第六轴法兰盘的中心位置(如图3所示)为工具坐标原点,相应的X轴、Y轴在法兰盘平面内,Z轴由右手定则决定,即为第六轴的轴线。如果机器人手臂末端需要安装工具的时候,使用者不再关心机器人第六轴法兰盘的位置和角度,而更关心焊枪、油漆喷头等工具最终的位置和角度,这时,就需要对工具坐标系进行赋值。工具坐标系记录执行工具的尺寸信息,其中包含toolx,tooly,toolz三个位置偏移信息和toolrx,toolry,toolrz三个角度旋转信息。这即说明,最终工具的工作点相对于图3所示的原点的位置偏移量为toolx,tooly,toolz,工具的工作轴线是绕相对于图3坐标系中的z轴旋转rz度,再绕y轴旋转ry度,再绕x轴旋转rx度得到。例如,本项目使用激光头作为工具,如图4所示,激光头的几何尺寸如图5所示。激光头的几何尺寸经过计算,激光头对应的工具坐标即为:toolx=-15.097;tooly=0;toolz=307.405;toolrx=0;toolry=35; toolrz=0。(实际中,机器人厂家可以通过五点示教的方法对工具坐标进行赋值,在此不再赘述)。

图4 机器人与工具(激光头)
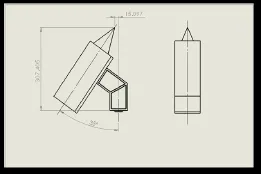
图5 激光头的关键几何尺寸
2 线性代数理论基础
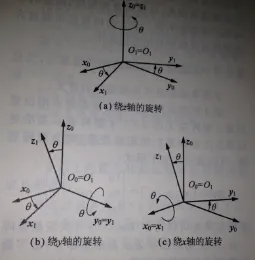
图6 坐标系旋转
3 已知关节坐标求解世界坐标
3.1 机器人尺寸和关节坐标与直角坐标
不带工具坐标系的机器人初始状态,即各关节j1,j2,j3,j4,j5,j6(单位为度)为0度位置,如7所示(图中长度数据单位为mm)。
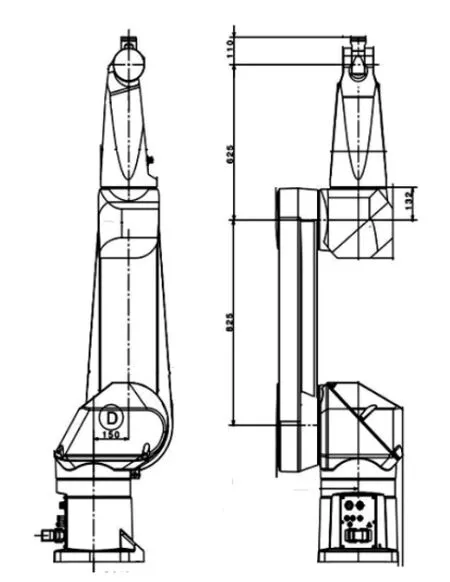
图7 机器人关键尺寸和初始姿态
当关节坐标j1,j2,j3,j4,j5,j6不为零时,机器人的工作状态如图8所示。
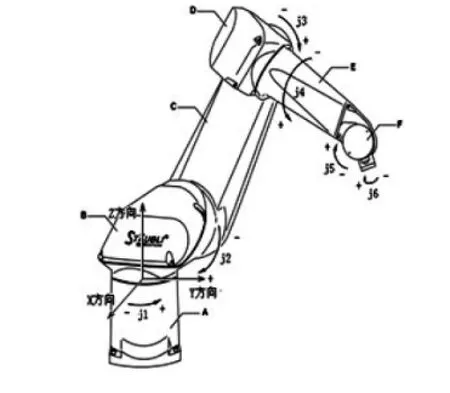
图8 机器人的一般工作姿态
3.2 不带工具坐标系的角度公式
对于图7所示的初始位置,机器人的第六轴竖直向上,指向Z轴正方向,用向量表示此方向为。而对于某个工作位置(图8),是由第一二三四五六各轴旋转角度为j1,j2,j3,j4,j5,j6得到的。
六个轴的旋转分六步。第六轴先旋转j6角度,相当于绕Z轴逆时针旋转j6度后,第六轴Z轴指向变为,同理,第五轴旋转j5角度后,第六轴Z轴指向相当于向量再绕X轴顺时针再旋转j5角度,用向量表示

第四轴的旋转j4角度相当于上述向量再绕Z轴逆时针旋转j4角度,第三轴的旋转相当于再绕X轴逆时针旋转j3角度,第二轴的旋转相当于再绕X轴逆时针旋转j2角度,第一轴的旋转相当于绕Z轴逆时针旋转j1角度,最终向量表示为
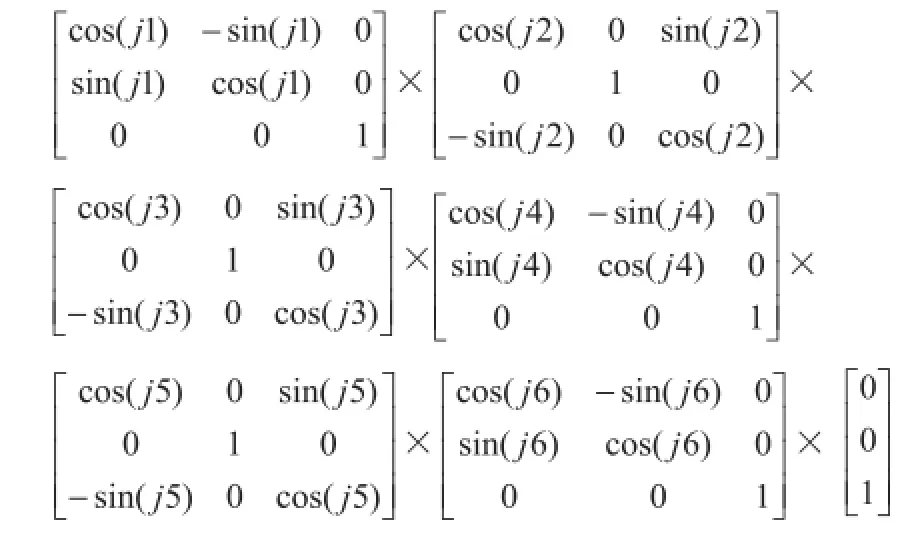
为了方便起见,不妨采用以下简化记法:


[j2矩阵]!= [j1矩阵]× [j2矩阵]
[j3矩阵]!= [j1矩阵]× [j2矩阵] × [j3矩阵]
[j4矩阵]!= [j1矩阵]× [j2矩阵] × [j3矩阵]× [j4矩阵]
[j5矩阵]!= [j1矩阵]× [j2矩阵] × [j3矩阵]× [j4矩阵]× [j5矩阵]
[j6矩阵]!= [j1矩阵]× [j2矩阵] × [j3矩阵]× [j4矩阵]× [j5矩阵] × [j6矩阵]
在7不带工具坐标的情况下,对于关节坐标为(j1,j2,j3,j4,j5,j6)的位置时,第六轴Z轴指向为
[j6矩阵]!×。

而在世界坐标系中,角度rx、ry、rz代表第六轴法兰盘轴线先后绕Z轴、Y轴和X轴旋转的角度。记:

[r矩阵]=[rx矩阵] ×[ry矩阵]×[rz矩阵]。
即,对于世界坐标(x,y,z,rx,ry,rz),是指第六轴轴线指向变为:
因此,已知关节坐标(j1,j2,j3,j4,j5,j6)求世界坐标系中的角度问题,即求rx、ry、rz的公式为:
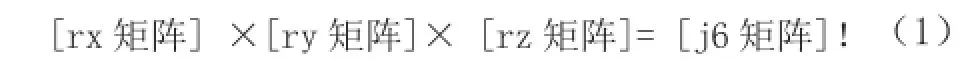
例如,当关节坐标为(10,20,30,40,50,60)时,求其世界坐标角度值rx、ry、rz。
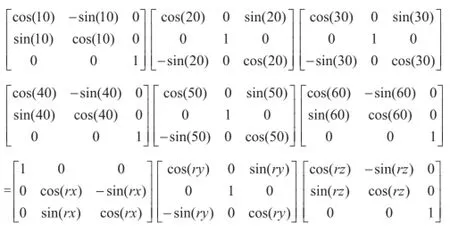
此方程展开后含有rx, ry, rz三个未知数及三个方程,因而可求。
3.3 不带工具坐标系的位置公式
机器人由六个关节组成,末端手臂的位置向量是这六个关节位置向量的矢量和。对于项目中的史陶比尔机器人,各关节的尺寸已知,如图7所示,不妨记x1=150,z2=825,z3=132,z4=625-132=493,z5=110。
第一关节:在j1角度为0的情况下,位置向量是在X轴正向偏移x1距离,而j1角度不为零时,位置向量则为[j1矩阵]×。
第四关节: j1,j2,j3,j4不为零时,位置向量为
第五关节: j1,j2,j3,j4,j5不为零时,位置向量为
第六关节:对于最终位置没有影响,位置向量为零。
综上所述,如果设世界坐标的位置为x、y、z,则已知关节坐标求解世界坐标(不带工具坐标系情况下)的位置公式为:

等式含三个方程,右侧皆已知,等式左侧含三个未知量x、y、z,因而可求。
因此,对于无工具坐标的情况,根据公式(1)和公式(2),如果已知关节坐标(j1,j2,j3,j4,j5,j6),则世界坐标(x,y,z,rx,ry,rz)可求。
3.4 带工具坐标系的角度公式
在实际工作中,机器人往往需要在第六轴上加装工具,即需要考虑工具坐标。本项目工具以激光头为例,工具坐标为:
toolx=-15.097,tooly=0,toolz=307.405,
toolrx=0,toolry=35,toolrz=0。
记:

[tool矩阵]= [toolrx矩阵] ×[toolry矩阵]× [toolrz矩阵]
则已知关节坐标求解世界坐标(带工具坐标系情况下)的角度公式为:

其中含有三个方程,三个未知数,[tool矩阵],[J6矩阵]!已知。方程可解。
3.5 带工具坐标系的位置公式
对于位置问题,可以认为前五个关节的向量相对于不带工具时没有变化,而由于工具坐标系位置向量的引入,使得第六关节的向量从0变为[j6矩阵]!×,最终已知关节坐标求解世界坐标(带工具坐标系情况下)的位置公式为:

(其中等式右侧均已知,x,y,z可求)
因此,对于带工具坐标的情况,根据公式(3)和公式(4),如果已知关节坐标(j1,j2,j3,j4,j5,j6),工具坐标(toolx,tooly,t oolz,toolrx,toolry,toolrz)则世界坐标(x,y,z,rx,ry,rz)可求。
4 已知世界坐标求解关节坐标
已知关节坐标,求解世界坐标是比较直观和简单的,而且实际意义不大,因为实际过程中往往是已知世界坐标而反求机器人的关节角度,所以下面论述已知世界坐标反求关节坐标的过程。
4.1 论题
举例来说,随意指定一世界坐标,如某一点A的世界坐标如下:x=1044.02,y=-89.64,z=984.62,rx=16.82,ry=77.02,rz=-16.73。工具坐标系已知如下:toolx=-15.097,tooly=0,toolz=307.405,toolrx=0,toolry=35,toolrz=0。机器人的必要尺寸已知:x1=150,z2=825,z3=132,z4=493,z5=110。求解为到达这一世界坐标点所需的各关节角度,即(j1,j2,j3,j4,j5,j6)的值。
4.2 求解方法
利用上述带工具坐标的两组方程,最终角度方程公式(3)和最终位置方程公式(4)求得。
4.3 求解过程
根据已知数据,计算出如下矩阵:

所以[j6矩阵]!与[j5矩阵]!的第三列是相等的,故第五关节向量中可以用 [j6矩阵]!代替[j5矩阵]!(这是很关键的一步简化,正是由于这步替代才使得方程最终可解)于是最终位置方程变成:
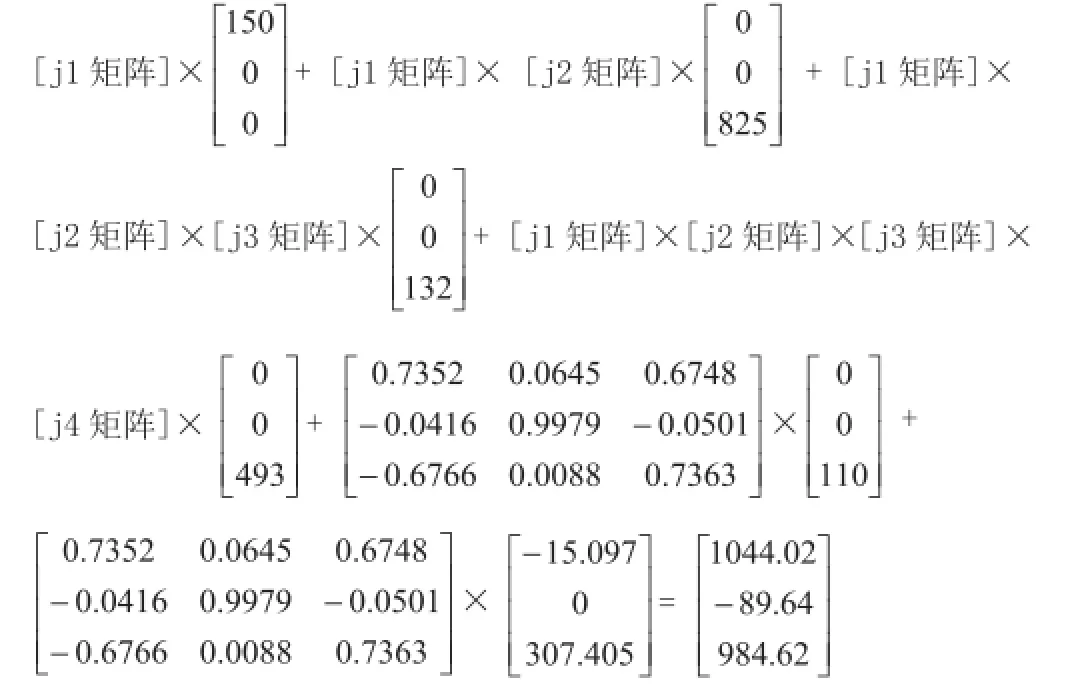
此含有三个方程,但是j1、j2、j3、j4共4个未知数,本不可解,但同样因为[j4矩阵]!与[j3矩阵]!第三列相同,所以j4这个未知数被消掉,上述方程变为含有3个未知数j1,j2,j3和三个方程,即:
150×cos(j1)+825×cos(j1)×sin(j2)+625×cos(j1)×cos(j2)× sin(j3)+625×cos(j1)×sin(j2)×cos(j3)+ 270.5762=1044.02 150×sin(j1)+825×sin(j1)×sin(j2)+625×sin(j1)×cos(j2)× sin(j3)+625×sin(j1)×sin(j2)×cos(j3)- 20.2935=-89.64 825×cos(j2)-625×sin(j2)×sin(j3)+625×cos(j2)× cos(j3)+317.5398=984.62
解此方程可以用通用的数学计算软件,如MATLAB编写程序求解,编写下列语句:
[j1,j2,j3]=solve('150×cos(j1)+825×cos(j1)×sin(j2)+625×cos(j1) ×cos(j2)×sin(j3)+625×cos(j1)×sin(j2)×cos(j3)+270.5762 =1044.02',
'150×sin(j1)+825×sin(j1)×sin(j2)+625×sin(j1)×cos(j2)× sin(j3)+625×sin(j1)×sin(j2)×cos(j3)-20.2935=-89.64', '825×cos(j2)-625×sin(j2)×sin(j3)+625×cos(j2)×cos(j3)+ 317.5398=984.62','j1','j2','j3')
MATLAB软件计算出j1,j2,j3的解,并转换成角度值得:

可见,每个角度的解并不唯一,各有四组解,但根据机器人使用常识可知,一般情况下有:
-90<j1<90,0<j2<90,0<j3<90故只有第二组解符合条件:
j1=-5.12340,j2=1.51080,j3=103.09769
再代入最终角度计算公式,可求j4,j5。同样,利用MATLAB软件编写下列语句:
[j4,j5]=solve('(-0.2512×cos(j4)+ 0.0893×sin(j4))×sin(j5)+ 0.9638×cos(j5)=0.6748','(0.0225×cos(j4)+ 0.9960×sin(j4))×sin(j5)- 0.0864×cos(j5)=-0.0501','j4','j5')
MATLAB软件计算出j4,j5的解,并转换成角度值得:
j4=179.32785,j5=62.03025
同理继续可求J6:
[j6]=solve('0.6766×cos(j6)+ 0.0114×sin(j6)=-0.6766','j6')
得: j6=-178.28299
故最终解为:
j1= -5.1234,j2=1.5108,j3=103.0976,j4=179.3278,j5=62.0302, j6=-178.2829。
4.4 验证过程
实际操作史陶比尔机器人,其带动激光头按照世界坐标移动到点(x=1044.02;y=-89.64;z=984.62;rx=16.82;ry=77 .02;rz=-16.73),如图9所示。之后,机器人的控制器切换到关节坐标模式,读取当前的关节坐标,如图10所示,(J1=-5.1239,J2=1.5119,J3=103.097,J4=179.328,J5=62.0318 ,J6=-178.30)。
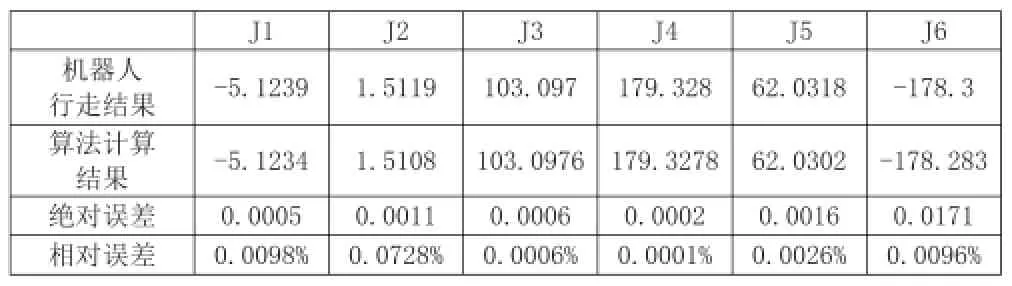
表1:机器人实际行走结果与本文算法结果的对比
表1为机器人实际行走结果与本文算法结果的对比,可以看出:机器人实际行走得到的结果与应用本文中的算法计算结果基本一致,误差低于千分之一。
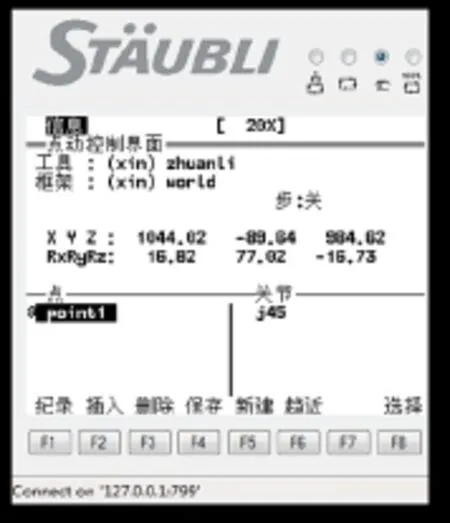
图9 机器人实际世界坐标
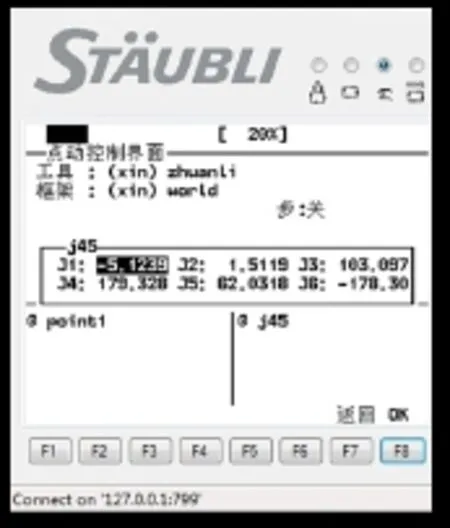
图10 机器人实际关节坐标
结 论
本文介绍的基于线性代数矩阵计算理论的求解机器人关节坐标和世界坐标的转换问题的方法,计算出的结果与机器人实际运行产生的结果一致。通过本算法,可以使机器人使用者更加深入地领会机器人的算法实质,不仅做到知其然,而且做到知其所以然。对于机器人选型,模拟仿真等工作也可以起到一定的帮助作用。
