基于可靠度的输变电设备检修策略优化
2014-04-20刘长银侯艳权姚越陈友李德煜李业勇
刘长银,侯艳权,姚越,陈友,李德煜,李业勇
(1.国网黑龙江省电力有限公司七台河供电公司,黑龙江七台河154600;2.山东大学电气工程学院,济南250001)
·专题论述·
基于可靠度的输变电设备检修策略优化
刘长银1,侯艳权1,姚越1,陈友1,李德煜1,李业勇2
(1.国网黑龙江省电力有限公司七台河供电公司,黑龙江七台河154600;2.山东大学电气工程学院,济南250001)
提出基于可靠度的输变电设备状态检修优化决策模型。首先,讨论计及检修策略的设备可靠度表达,并基于此对前瞻时间内设备可用度进行求解,从而在给定设备检修策略的前提下,对电网整体的故障风险和检修风险进行量化,最后,以电网总风险最小为目标,计及状态检修的约束条件,形成电网状态检修的数学模型,并采用遗传算法进行求解,通过IEEERTS79系统算例分析表明模型的可行性、有效性。
电力系统;状态检修;可靠度;故障风险;检修风险
0 引言
状态检修依据设备在线监测及预测技术获得的设备状态信息,在设备发生故障前实施检修。相比传统的定期检修、以可靠性为中心的检修方式,状态检修可以显著提高电网整体运行的可靠性和经济性,目前已经成为研究的热点问题[1-3]。
就设备状态检修而言,现有研究倾向于从设备个体角度出发制定其检修策略[4-6],然而,该类研究未能考虑电网运行中设备间的关联性(经济关联、随机关联、功能关联),以及设备和系统之间的协调性。因此,做出的决策结果较容易引起较大的系统损失,有必要将设备的检修策略从系统整体的角度予以重新审视[7-10]。对此,文献[11]提出电网状态检修的概念,建立了电网状态检修风险和故障风险的表达,对电网运行中设备间存在的功能关联、经济关联以及随机关联等进行了较为深入的分析。电网状态检修决策极具复杂性,研究目标为对前瞻时间内的电网检修风险和故障风险进行折中,但仅针对设备的单个检修计划进行检修决策,未研究设备实施不同检修策略对电网运行风险的影响。将就设备检修策略与电网运行风险间的关系展开。
在已有研究基础上,给出前瞻时间内计及检修策略时设备可靠度和可用度的函数表达式,并基于此对不同检修策略引起的电网故障风险和检修风险进行量化,然后以二者之和最小为目标,计及电网状态检修的约束条件,建立状态检修的数学模型,给出其具体求解步骤,通过对各种情况进行分析,验证了研究方法的可行性和有效性。
1 设备状态表达
1.1 设备的可靠度
输变电设备在运行过程中,随机因素和自然老化都有可能使设备发生故障。随机故障不能预测,无法通过预防性检修改变其故障率;老化故障可以通过预防性检修减小设备老化故障概率,提高其可靠性。据此考虑老化的影响,通过威布分布描述设备可靠度,则自设备初始投运时起,设备可靠度表达为[12-13]
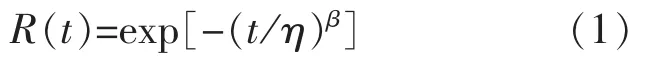
式中:β和η分别为威布分布的形状参数和尺度参数。
前瞻时间内,通过计划检修,可以延长设备的使用寿命,提高其可靠度,检修引起的设备可靠度变化取决于所采用的检修策略,通过役龄回退模型[14]可以定量描述计划检修对设备可靠度的影响。图1为前瞻时间内计及检修策略时设备的可靠度变化曲线,图中0为前瞻时间初始时刻,t0为设备上一次检修对应的时刻,tk(k≥1)为前瞻时间内第k次检修时刻,τk(k≥0)为前瞻时间内第次检修对应的设备停运持续时间。

图1 设备可靠度变化曲线
前瞻时间内,对应某一检修策略,在设备初始性能给定前提下,其可靠度表达为

式中:tact为时刻t0设备检修之后的等效役龄;θj为设备第j次检修的役龄回退因子;Tk为设备第k次检修之后的等效役龄。
1.2 前瞻时间内设备可靠度求解
前瞻时间内,计及检修策略求取设备的可靠度,要考虑设备运行历史对当前状态的影响。因此,设备可靠度应表示为条件概率,针对以下3种情况讨论前瞻时间内设备可靠度表达。
1)前瞻时间内设备不检修。
该情况发生时,在给定设备初始可靠度前提下,令变量Rc,i(t)表示设备可靠运行至前瞻时间内时刻t的概率,由条件概率公式,得
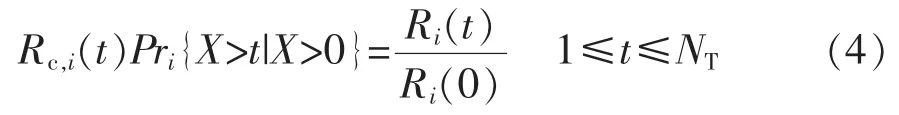
式中:X为设备i的寿命;NT为前瞻时间划分的时段数目。
2)前瞻时间内只考虑设备单个检修计划。
该情况发生时,在计划检修时刻t1到来之前,设备可靠工作的概率与情况1类似,表达式为

计划检修时段[t1,t1+τ1)内,设备检修停运,此时,其可靠工作的概率为

计划检修完成后,设备i重新投入运行,此时,设备可靠工作的概率表示为该计划检修事件的条件概率,表达式为
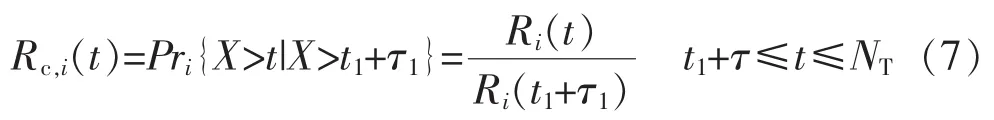
综上所述,前瞻时间内时刻t设备i可靠工作的概率如式(8),该函数表达式与计划检修起始时间t1和持续时间τ1有关。
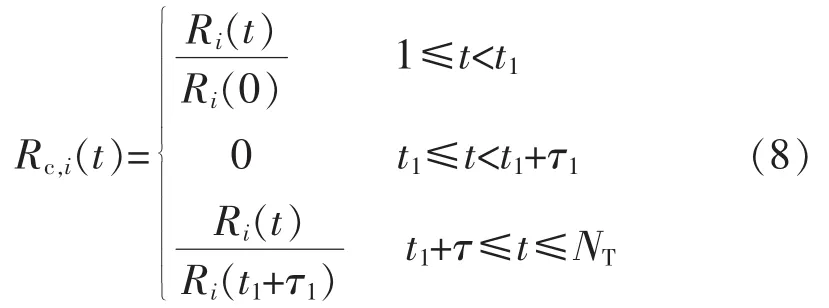
3)综合以上2种情况,前瞻时间内当考虑设备多个检修计划时(记为n个),根据数学归纳法可得设备i可靠工作的概率表达为
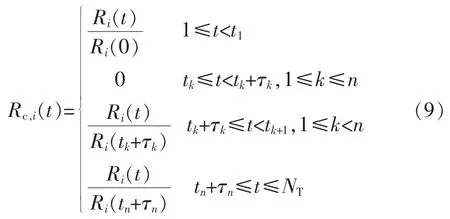
在式(9)基础上,得前瞻时间内任一时段设备的故障概率为
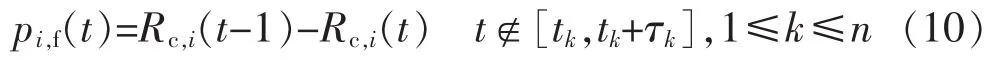
1.3 前瞻时间内设备可用度求解
上节求取设备可靠度只考虑了设备计划检修停运,前瞻时间内为得到设备的可用度函数,还要考虑设备故障后维修。下面讨论设备的可用度函数表达式。分为2种情况。
1)时段t设备i未安排计划检修。
在已知时段t设备未进行计划检修前提下,该时段设备i的平均无故障工作时间为[15-16]

时段设备的平均故障修复时间为

式中:τi,f表示设备i故障后维修时间。
由此,可得时段t设备的可用度函数为
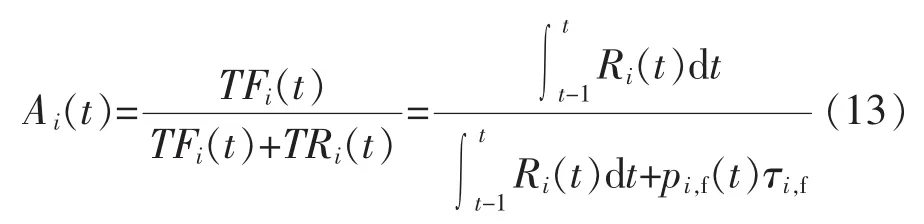
2)时段t设备i计划停运。
该情况发生时设备i的可用度为

2 电网检修风险和故障风险
2.1 电网故障风险
前瞻时间内,给定输变电设备检修策略前提下,计算电网故障风险要利用上文的设备可靠度和可用度指标,从概率和后果的角度综合度量,电网故障风险具体表达为

式中:RIF,1(t)和RIF,2(t)分别为时段t的设备个体损失和电网损失;NM为电网中输变电设备总数目;Ci,f为设备故障费用;S(t)为时段t计及设备检修停运的电网事故集合;Ps(t)为时段t事故s发生的概率;sevs(0,t)为时段t不考虑设备检修停运,事故引起的电网失负荷量;cf为电网单位失负荷损失。
时段t事故s发生的概率为

式中:N(t)-Nf(t)和Nf(t)分别为时段t事故s中可用和不可用的设备数目。
2.2 电网检修风险
前瞻时间内,检修风险与故障风险相互牵制,表示输变电设备检修引起损失,与故障风险类似,包括设备个体检修损失和电网检修损失,二者统一的数学表达为

式中:RIM,1(t)和RIM,2(t)分别为时段t输变电设备检修引起的设备个体损失和电网损失;Xi,t为时段t设备i的状态变量,Xi,t=0表示时段t设备i不检修,Xi,t=1表示时段t设备i进行检修;Ci,m为设备i的预防性检修费用;sevs(m,t)为时段t计及设备检修停运事故s引起的电网失负荷量。
3 电网状态检修决策的数学模型
前瞻时间内,针对电网中全部设备,以电网检修风险和故障风险二者之和最小为目标,建立电网状态检修的数学模型。表示为

满足如下约束。
1)检修资源约束。
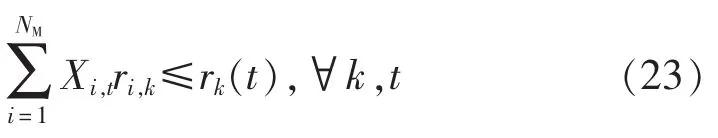
式中:ri,k为设备i检修时对资源k的需求量;rk为时段t资源k的可用量。
2)设备同时检修约束。对导致电网重复停电的设备同时进行检修有利于减少系统损失,满足

4 模型的求解
电网状态检修决策可以分解为一个主问题和一个子问题。主问题选择设备的检修策略,目标是使前瞻时间内电网检修风险和故障风险二者之和最小,因此它是一个含有离散变量的复杂的组合优化问题,借助遗传算法实现;子问题在各时段内,根据主问题给定的设备检修策略,求取每一事故对应的电网最优切负荷,以确定各时段电网的检修风险和故障风险,可采用直流优化潮流模型求解。借鉴文献[11]给出模型的求解方法。
1)形成初始种群,种群中每个个体采用矩阵编码,如式(25)所示。

式中:gi对应前瞻时间内设备i的检修策略。
2)校验种群中任一个体是否满足电网状态检修的约束条件,若满足,则计算该个体对应的电网检修风险和故障风险作为其适应度值;否则,直接赋一较大数值作为该个体对应的适应度值。
3)判断是否满足终止条件,若满足,则将适应度值最小的个体作为问题的解;否则,个体间进行交叉、变异,重新生成新的种群,返回步骤2。
5 算例分析
为验证模型的有效性,本算例采用IEEE-RTS79系统进行分析。该系统为一个24节点的可靠性测试系统,包含26台发电机,38条输电支路和5台变压器。为侧重机理分析,前瞻时间内仅对设备3~24和设备9~12进行检修决策,设备状态相关信息见表1,算例其它原始数据可见文献[17]。前瞻时间为1年,划分为52个时段,各设备检修持续时间为1周,电网单位失负荷损失cf为1.053万元/(MW·h)。
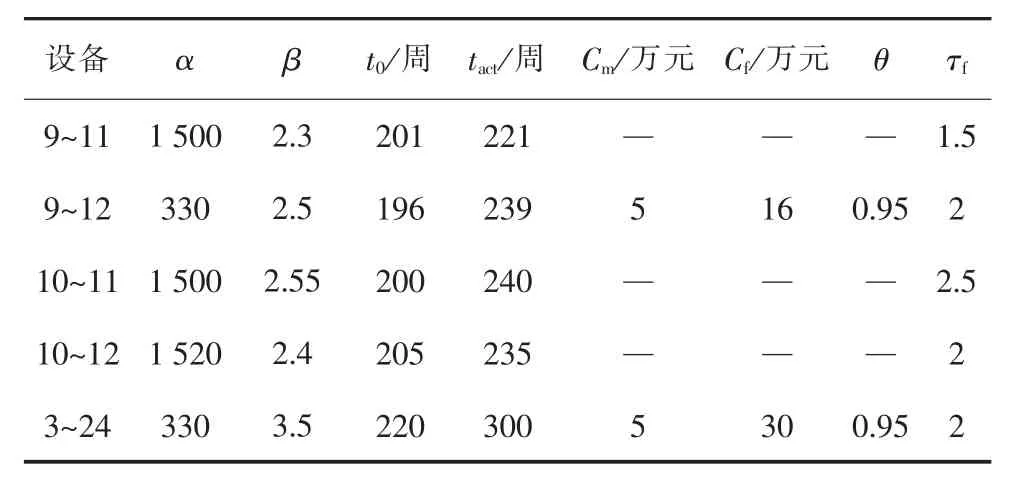
表1 IEEE-RTS79系统设备状态信息
5.1 设备检修策略与电网运行风险间的关系
为对设备检修策略与电网运行风险间的关系进行量化,根据设备所实施的检修策略不同,该算例对4种方案进行了分析。方案2中设备均采用事后检修策略,方案2中设备均采用定期检修策略,方案3按设备个体性能进行检修决策,方案4为本文模型。
对上述4种方案进行求解,表2给出了4种方案下的设备检修时机、电网的检修风险和故障风险。
方案1。前瞻时间内电网设备均不检修,因此,该方案下电网检修风险为0,但由于前瞻时间内电网故障损失较大,因而该方案对应的电网总风险最高。
方案2。在定期检修框架下,前瞻时间内设备3~24和设备9~12均安排1次计划检修,设备检修时机选择电网负荷较低的时段,分别为第12周和42周,由表2的计算结果可以看出,方案2相比方案1,检修风险的增加程度小于故障风险的降低程度,二者之和降低35.5%。
方案3。当仅考虑设备个体性能时,设备个体的检修风险、故障风险成为检修决策的主要矛盾,由结果可以看出,设备3~24性能较差,在前瞻时间初始时段开始检修,降低了设备状态劣化的可能性;设备9~12性能较好,前瞻时间内不检修,此时,设备个体检修风险与故障风险之和是最低的。
方案4。在方案3基础上,计及设备间关联性以及电网运行方式的影响,该方案就如何降低电网运行风险较设备个体检修风险与故障风险而言,是检修决策的主要矛盾,从表2的结果可以看出,前瞻时间内设备3~24安排2次计划检修,其中第1次计划检修从第1周延后到第12周,第2次检修时机为第42周,设备9~12在第13周安排1次计划检修,设备检修时机均向电网负荷较低的时段偏移。
结果表明:不同检修策略对电网运行风险的影响不同,对比方案4和方案2,定期检修无法考虑设备性能变化规律,导致协调设备检修与电网运行间关系的能力大幅降低,前瞻时间内电网总风险较大;方案4相比方案3,检修风险和故障风险均有所降低,电网总风险降低34.9%,说明方案4可以有效协调设备个体间、设备个体与电网运行间的关联性,这也体现了研究的意义。
5.2 设备性能变化对检修时机的影响
进一步分析设备性能变化对检修时机的影响,假设设备3~24前瞻时间内可靠度有所提高,相应的威布分布参数α=405,β=3.5,其它设备状态信息见表1,重新求解本文电网状态检修决策模型,记为方案5,表3给出对应的计算结果。
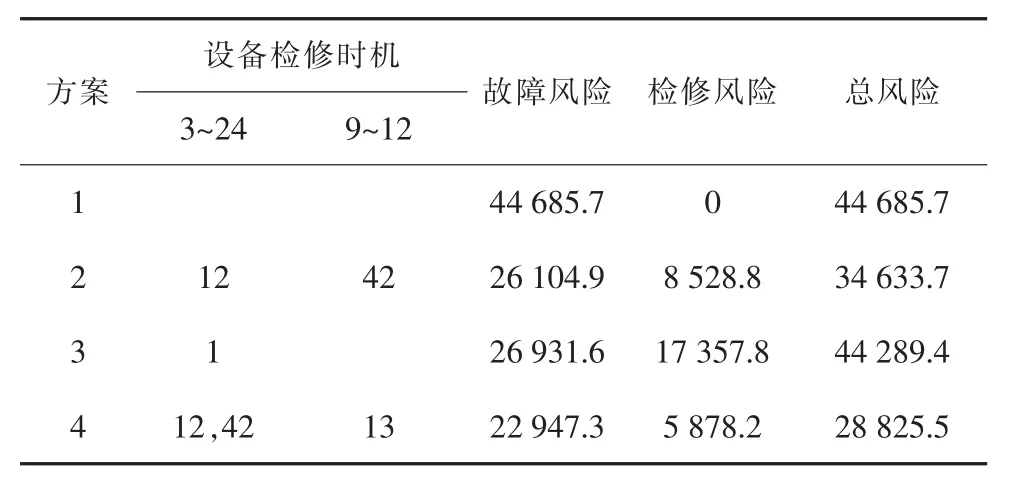
表2 IEEE-RTS79系统设备检修策略对比
方案5相比方案4,设备3~24个体性能有所提高,由于设备3~24不可靠工作引发的停电可能性大大减少,前瞻时间内设备3~24只在第15周安排1次计划检修,而设备9~12检修时机不变,电网总风险有所降低。

表3 设备性能变化对检修计划的影响
5.3 约束条件对设备检修时机的影响
进一步分析约束条件对设备检修时机的影响,假设前瞻时间内由于电网检修资源的限制,时段12以前无法对电网中的设备实施检修,在此基础上,对设备3~24和设备9~12进行检修决策,记为方案6,表4给出检修资源受限情况下设备检修开始时段以及电网的风险指标。可以看出,相比方案4,方案6中设备3~24第1次检修的时机从第12周延后到第13周,设备9~12的检修计划取消,数据表明方案6对应的电网总风险高于方案4。

表4 约束条件对设备检修计划的影响
6 结语
研究的电网风险计算方法可以有效地协调设备检修与电网运行之间的矛盾和冲突。就所述模型而言,待检修的设备集合可以自动确定,有利于提高电网运行的可靠性、灵活性和经济性。实现了设备状态检修与电网运行决策间的进一步融合,具有良好的应用前景。
[1]刘建胜,酆达,张凡.一种用于变电站高压触点温度在线监测的新方法[J].电力系统自动化,2004,28(4):54-57.
[2]韩学军,刘滨涛,陈永辉,等.基于无线通信的高压断路器温度在线监测系统[J].电力系统自动化,2006,30(8):84-88.
[3]李明,韩学山,王勇,等.变电站状态检修决策模型与求解[J].中国电机工程学报,2012,32(25):196-202.
[4]廖瑞金,王谦,骆思佳,等.基于模糊综合评判的电力变压器运行状态评估模型[J].电力系统自动化,2008,32(3):70-75.
[5]吕超,于洪梅,王立欣.基于人工免疫网络的断路器在线自学习故障诊断[J].中国电机工程学报,2010,29(34):128-134.
[6]Chen Dongyan,Kishor S.Trivedi.Optimization for condition-based maintenance with semi-Markov decision process[J].Reliability Engineering and System Safety,2005,90:25-29.
[7]赵明欣,鲁宗相,吴林林,等.基于风险评估的输变电设备维修技术[J].电力系统自动化,2009,33(19):30-35.
[8]潘乐真,鲁国起,张焰,等.基于风险综合评判的设备状态检修决策优化[J].电力系统自动化,2010,34(11):28-32,66.
[9]张大波,李文沅,熊小伏.基于状态监测的多目标双层优化待修架空线选择模型[J].电力系统自动化,2013,37(2):23-27.
[10]Camci F.System maintenance scheduling with prognostics information using genetic algorithm[J].IEEE Transactions on Reliability,2009,58(3):539-552.
[11]李明,韩学山,杨明,等.电网状态检修概念与理论基础研究[J].中国电机工程学报,2011,31(34):43-52.
[12]Tsai Y,Wang K,Tsai L.A study of availability-centered preventive maintenance for multi-component systems[J].Reliability Engineering and System Safety,2004,84:261-270.
[13]YanJihong,HuaDingguo,WangZimo.Reuseorientedgroup maintenance scheduling based on Hybrid Genetic Algorithm and Tabu Search[C].IEEM 2011:1 524-1 528.
[14]Levitin G.Lisnianski A.Optimization of imperfect preventive main tenance for multi-state systems[J].Reliability Engineering and System Safety,2000,67:193-203.
[15]Lapa C.M.F.,Pereira C.M.N.A.,de Barros M.P.A model for preventive maintenance planning by genetic algorithms based in cost and reliability[J].Reliability Engineering and System Safety,2006,91(2):233-240.
[16]Mijailovic V.Optimal spares availability strategy for power trans former components[J].Electric Power System Research,2010(80):987-992.
[17]Billiton R,Kumar S,Chowdhury N,et al.A reliability test system for educational purposes-basic data[J].IEEE Transactions on Power Systems,1989,4(3):1 238-1 244.
Decision-making of Condition-based Maintenance for Power System Based on Equipment Reliability
A methodology for condition-based equipment maintenance optimization is presented based on equipment reliability. Firstly,equipment reliability expression is given considering maintenance strategy during the maintenance scheduling period. Then,equipment instantaneous availability function is obtained.Maintenance strategy,power system failure risk and maintenance risk are calculated.Finally,with constraints of the maintenance taken into account,system maintenance model which is solved by genetic algorithm is established to minimize total power system risk.The IEEE-RTS79 test system is used to verify feasibility and effectiveness of the proposed model.
power system;condition based maintenance;reliability;failure risk;maintenance risk
TM72
:A
:1007-9904(2014)06-0021-05
2014-08-08
刘长银(1960),男,高工,研究方向为信息化建设;
侯艳权(1983),男,助理工程师,研究方向为信息化建设;
姚越(1986),男,助理工程师,研究方向为电力系统调度自动化;
陈友(1979),男,工程师,研究方向为电力系统调度自动化;
李德煜(1971),男,工程师,研究方向为电力系统调度自动化;
李业勇(1990),男,硕士研究生,研究方向为电力系统可靠性与检修研究。
