玩不厌的数字游戏

李开国

玩不厌的数字游戏

>>帕斯卡

李开国

【二项式定理】

二项式定理又叫牛顿二项式定理，是指(a+b)n=Cn0an+C1nan-1b1+Cn2an-2b2+…+Cnran-rbr+…+Cnnbn这样一个展开式的公式。它是(a+b)2=a2+2ab+b2，(a+b)3=a3+3a2b+3ab2+b3等展开式的一般形式。

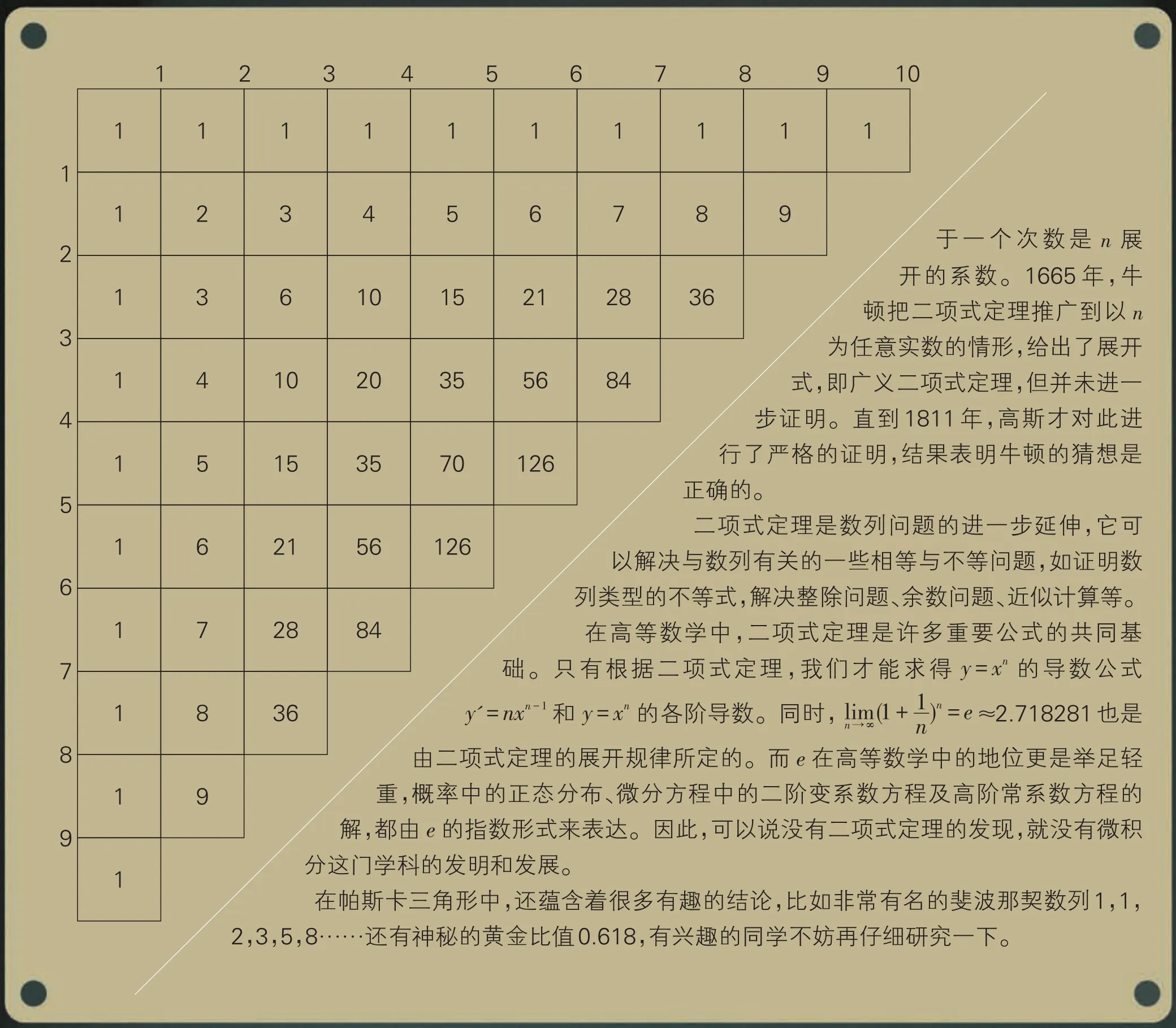
很多同学都玩过找规律的数字游戏吧？这个图就是有名的帕斯卡三角形，是帕斯卡在玩数字游戏时发明的。一天，帕斯卡在纸上用1、1、1、1……写下了水平和垂直的数列，使之成一个倒L字图形。接着，他在第二行第二列，写上第一行第二位数加上第二行第一位数的和2，即1+1=2；在第二行第三列，写上之前那个数加上第一行第三位数的和3，即2＋1=3。这样依次下去，到9为止。然后，他在第三行第二列，写上第三行第一位数加上第二行第二位数的和3，即1+2=3；在第三行第三列，写上之前那个数加上第二行第三位数的和6，即3+3=6……一直进行这种锯齿形的加法，最后得到的图形就是帕斯卡三角形。

其实，类似的数字三角形并非是帕斯卡最先发明的，只是起初没有被广泛流传罢了。1527年，德国数学家阿皮安努斯出版了自己的著作，其封面上就刻有此图，而帕斯卡在1654年才得出了这个图形。

仔细观察帕斯卡三角形，我们会发现从右上角到左下角的对角线所经过的数字，恰好是二项式定理对

【小链接】

二项式定理左边是两项和的幂的形式，右边共有（n+1）项；右边既可以看成是字母a的降幂排列，次数由n递减到0，又可以看成是字母b的升幂排列，次数由0递增到n，每一项都是n次的齐次式。

对称性

与首末两端“等距离”的两个二项式系数相等，这一性质可直接由公式Cmn=Cnn-m得到。

增减性与最大值