CFE条件下基于循环维纳滤波的单通道分离算法

宋 阳，王 翔，马忠正，王丰华，黄知涛

(国防科技大学电子科学与工程学院，长沙 410073)

0 引言

航天测控与通信系统，按照国际惯例统称为C＆T系统，即通信与跟踪系统，包含空间段和地面段设备两部分，两部分相互配合工作，以完成测量运载火箭的轨迹和航天器入轨后的轨道，并将运载器和航天器(S/C)上各分系统的工作状况传回地面。通信则负责将航天器上测量、观察仪器所获得的信息和数据传回地面地球站，其中含话音(audio)、视频(video)、静止图像等CCSDS(空间数据系统协商委员会)提出的统一数据流。数传信息则包括由遥测信息，测角信息、测速信息、测距信息和通信信息等组成的一系列下行数据信息，在数据信号接收的过程中经常会出现多个信号同时被接收机主瓣波束接收进来，造成信号时频域混叠的现象。因此，在未知源信号和混合参数的情况下，研究单通道的盲信号分离方法，具有良好的实际意义。

信号处理中可以通过设计各种形式的带通滤波器进行频域滤波从而逐个分离单通道频域不重叠的平稳随机信号;也可以通过时域数据分段截取处理的方法(类似于短时开关)逐个提取单通道时域不重叠的信号。然而实际中，单通道接收到的混合信号一般是时频重叠的，传统的时域频域滤波法已经无法对这种信号分离提取。James R.Hopgood［1］进一步推广了时域频域理想滤波的概念，提出了广义谱域的概念，并指出，如果存在一个广义谱域，且源信号相互不重叠，通过构造广义谱域上的线性时变维纳滤波器(广义理想带通滤波器)就能完成多信号分量的分离。因此，单通道时频重叠信号的分离问题可以转换为寻找一个新的变换域，并构造该域上的理想滤波器来完成，由于实际中，除了目标信号(SOI，signal of interest)的循环频率作为先验信息，其余信号的循环频率未必事前已知，无法通过多次滤波逐个提取，针对这种情况可以采用对消的方法对观测信号进行消除源信号提取剩余源信号。

实际中已经验证大多数航天测控数传、通信信号表现了很强的循环平稳特性，在源信号时频重叠的情况下，如果其循环频率相互之间互素，信号的循环谱就会不发生重叠。已有的滤波方法主要是经典的LCL-FRESH滤波理论［2］，依据的是循环平稳信号的瞬时谱平移特定值后得到的瞬时谱与原信号谱仍然相关，通过对原信号瞬时谱与信号平移后的瞬时谱进行适当的加权处理，就能增强或减弱特定频率分量的信号。然而由于信号和干扰的循环频率(CF，cycle frequency)是在一些特定的频率上离散分布的，只有经过特定频移的信号才具有相关性，这就导致了LCL-FRESH滤波器的性能对CFE十分敏感。目前有关LCL-FRESH滤波器的研究文献通常都基于接收机准确指导信号或干扰CF已知的假设，这是理想情况下的LCL-FRESH滤波，针对存在CFE时的LCL-FRESH滤波器性能研究较少。文献［3］提出CFE的校正算法，该算法利用文献［4］提出的TA-MSE作为代价函数，采用固定的J个输入样点对TA-MSE进行估计，然而并未对 J个输入样点的选取进行约束，未充分利用全部观测样本数据，CFE校正时存在一定的偏差。基于LCL-FRESH滤波器对复杂航天数传通信信号干扰抑制的模型，首先从循环频域理想滤波的角度出发，分析了线性-共轭-线性频移滤波器用于单通道盲信号分离的可行性，简单给出了CFE对LCL-FRESH滤波器性能的影响，提出了一种改进的CFE校正条件下，基于循环频移滤波及Schmidt正交化对消算法，并通过仿真验证本文算法的有效性。本文的结构是:第2节介绍信号、系统模型，进行问题描述。第3节分析LCL-FRESH滤波的可行性及给出CFE对LCL-FRESH滤波性能的影响;第4节提出一种改进的CFE校正算法;第5节给出CFE下LCL-FRESH滤波器性能的数值仿真结果;第6节对所研究的工作进行总结。

1 信号及系统模型

1.1 循环平稳信号概述

所谓循环平稳信号是一类非平稳信号，但是其统计特性随时间周期性的变化，即:如果［x(t)］为二阶的循环平稳信号是指其时变均值和自相关函数都为时间的周期函数，这类信号称为“循环平稳”信号［2］。如果一个随机过程x(t)是二阶广义循环平稳的，意味着其自相关函数具有周期性，即满足

对 Rx(t，τ)进行 Fourier级数展开，得

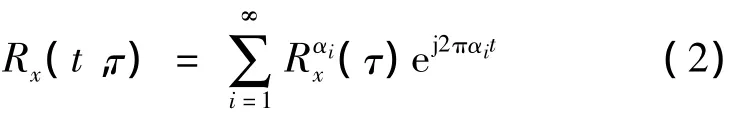
第i个Fourier系数为

式中，(·)*表示取共轭;表示求时间平均;αi称为循环频率。(τ)也称为循环自相关函数。信号的循环谱定义为(τ)的Fourier变换，即

特别地，当αi=0时，循环谱退化为信号功率谱，即

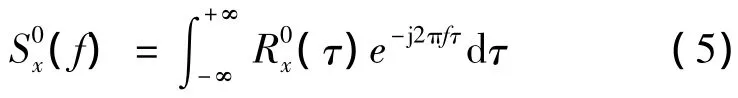
W.A.Gardner教授［2，5］揭示了循环平稳信号的本质特征，即将信号的瞬时谱在频率上分别上下搬移一定值后的两个信号具有相关性，而搬移的频率值就是信号的循环频率，并进一步指出，利用这种谱相关性可以实现信号分离。

1.2 循环维纳滤波结构

考虑一个单通道输入信号x(t)的情况，它由源信号信号s(t)和白噪声n(t)组成，单通道的混合信号模型可以写为

式中，x(t)表示观测信号;s(t)=［s1(t)，…，sN(t)］T是N 个窄带源信号;a=［a1，a2…，aN］T表示混合系数。单通道盲信号分离就是在未知混合系数a和源信号s(t)的情况下，仅利用x(t)估计出源信号。由于白噪声是非循环平稳信号，文献［6］指出在源信号循环频率不为零的地方，白噪声谱频率分量影响相对较小，特别是当信号积累实践足够长时，这种影响完全消失。假设接收信号的数据长度为L，那么它需要利用L个已知量去估计L×N个未知量。本研究只针对两个源信号的情况进行分析。此时，式(6)可以简化为

本算法采用线性共轭线性-频移(LCL-FRESH)滤波器，滤波器结构如图1所示，由于实信号的线性时变滤波等效于对其复包络(或解析信号)及其复包络的复共轭分别进行线性时变滤波。因此对于复信号，最佳的自适应时变滤波则是将信号与其共轭联合滤波，再加权求和，即线性-共轭-线性(LCL，linear-conjugate-linear)滤波器。输入信号的频谱表达为

最佳的LCL-FRESH滤波问题就等效于多变量的维纳滤波器系数求解问题。该滤波算法通过循环维纳滤波的方式分离频谱交叠信号，叠加有用倍频信号能量，再经过一组线性时不变滤波器加权求和，有效提高了接收信号的信干比。在通信系统抗干扰设计中，基于复信号的算法具有实用价值。根据最小均方误差准则，最优滤波器响应可表示为

1.3 Schmidt正交对消结构

接上节的信号处理，如果利用s1(k)的频率和符号速率就能设计出对应s1(k)的LCL-FRESH的滤波器hopts1(k)，从混合信号中提取s1(k)。设(k)表示LCL-FRESH滤波器提取的s1(k)的估计，则有

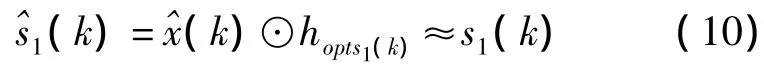
由于在实际情况中并不是所有的源信号都能估计出其频率和码速率，因此无法使用FRESH滤波器一个个将信号滤除出来，针对这种情况，现有的文献［7］采用基于Schmidt对消的思想，如果能从观测信号中消除LCL-FRESH滤波器提取的源信号，则剩余信号即为另一个源信号。该算法流程如下。

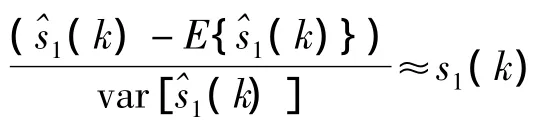
2 误差条件下循环频域滤波可行性分析

在实际的信号接收处理中，信号在传输、接收的过程中不可避免的会带来一定的系统误差，这种误差最明显的表现在循环频率上，文献［3］已证明LCL-FRESH滤波对循环频率非常敏感，当存在CFE时，假设FRESH滤波器循环频率为αm的支路上存在循环频率误差ΔF，则该支路的输入信号矢量可以表示成

当ΔFm＜＜αm且n较大时

考虑式(14)，当存在CFE时对源信号

比较式(10)和式(15)可以发现，存在CFE时源信号支路输出与不存在CFE之间产生了一个相移因子，该相移值的大小和CFE与时间的乘积有关，在CFE固定的情况下，相移值大小随时间的增加而线性增加，由于信号的循环频率是在一些特定的频率上离散分布的，只有经过特定频移的信号才具有相关性，致使该支路的输出逐渐偏离其正确的相位，与FRESH滤波器其他支路不再满足严格的同相叠加关系，从而使滤波器的输出估计误差增加，性能下降。

可见当CFE很小时，相位偏离随时间的增加而增加得十分缓慢，由于相位偏离很小，对该支路的影响也就很小，在滤波器自适应调整开始的一段时间内，该支FIR滤波器的调整过程与无CFE的理想情况很接近，其FIR滤波器的抽头系数将趋向于无CFE时该支路FIR滤波器的最佳抽头系数，即

这时该支路与理想输出间的误差为

对应的均方误差为

可见，当存在CFE时，该支路的输出受到ΔFm的影响，ΔFm越大，均方误差加权因子也就越大，该支路FIR滤波器的输出与理论值的偏差也就越大，从而使FRESH整体估计误差增加，这就导致了滤波性能的下降。

3 一种改进的CFE校正算法

通过上面的分析表明，FRESH滤波器的性能对CFE十分敏感，当CFE很小时，其性能与没有CFE的理想情况相接近，但是随着CFE的增大，FRESH滤波器的性能迅速变差，为了对盲分离的效果进行评估，采用信干比SIR作为恢复出的信号波形与源信号波形之间的差异性的评价。SIR定义为

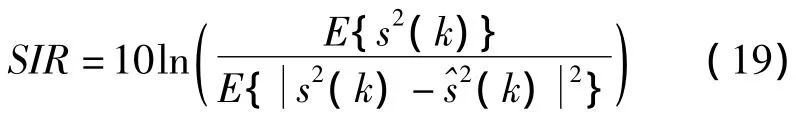
s2(t)在s1(t)的循环频率2R1和2f1+2R1处的循环谱，如图2和图3所示。从图中可以看出，s2(t)与s1(t)在循环频率α处的循环谱主瓣峰值相差20 dB以上，因此可以对上述信号进行分离，接着考虑CFE对滤波性能的影响，观察信号s1(t)在自身循环频率附近的循环谱。

信号s1(t)在循环频率为α1=2f1+2R1，循环频率误差ΔF=10 Hz处的循环谱，如图4所示。由图4可见二者相差不大，与前文分析一致，当CFE较小时对滤波器性能的影响较小。信号s1(t)在循环频率为 α1=2f1+2R1，循环频率误差 ΔF=3.245 MHz处的循环谱，如图5所示。由图5可见信号s1(t)的循环谱主瓣峰值已有将近10 dB的差异，这对滤波器的性能将会产生很大的影响。

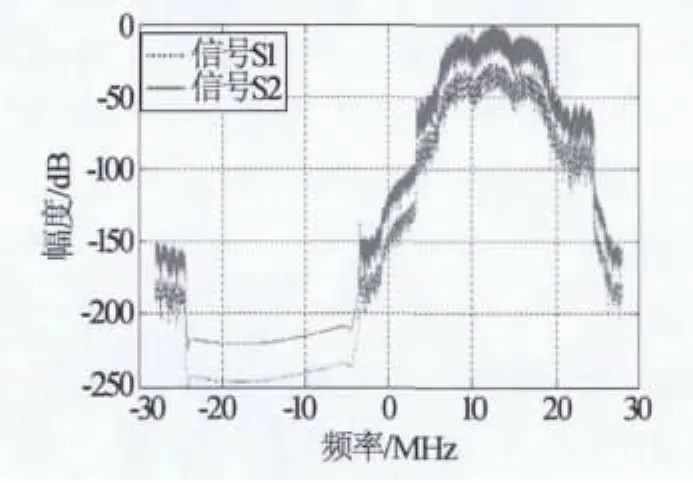
图2 源信号在2R1处的循环谱

图3 源信号在2f1+2R1处的循环谱

4 源信号在循环频率ΔF=10 Hz处的循环谱

图5 源信号在循环频率ΔF=3.245 MHz处的循环谱

文献［4］以MSE作为代价函数，通过修改最陡下降算法，提出了一种CFE的自适应校正方法，该算法表示为

式中，γ表示用作FRESH滤波器频移的信号或干扰的CF;μγ表示迭代步长，控制收敛速度和稳态精度;sign(·)是符号函数;ε(n)是基于当前最近的J个样点对MSE的估计。这种算法的思想简单，通过调整CFE的大小，使MSE向着减小的方向变化，然而该算法采用的是最近的J个样点作为估计量，并没有充分利用观测量，如果CFE较小的情况下，前文已分析较小CFE下对信号的MSE改变影响较小，致使干扰样点和噪声的输入会对MSE变化产生更大的影响，算法的梯度方向会发生改变，致使无法收敛。针对这种情况本文提出了对这种算法的改进，代价函数仍然采用MSE最小代价函数，但是在迭代的过程将本次观测的所有N个样点全部统计进来用于函数的迭代计算，相当于利用全部的输入样点对MSE进行训练，使每次的迭代过程ε(n)的变化完全是由CFE的改变而引起。改进算法表示为

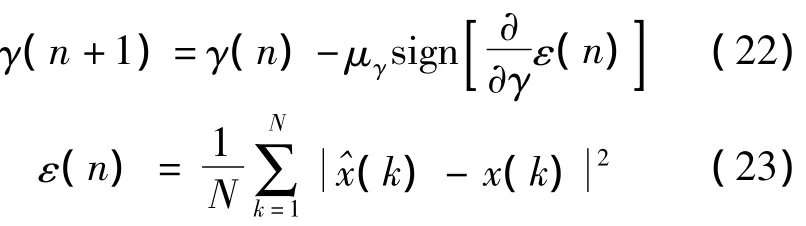
4 算法步骤

综上所述，算法流程如图6所示。具体步骤可总结如下。

(1)把观测信号进行Hilbert变换，得到解析信号;

(2)根据其中一个源信号s1(k)的循环频率，确定非共轭部分频率{αi}N和共轭部分频率{βi}M，在共轭循环频率中引入循环频率误差ΔF;

(3)根据式(22)、式(23)迭代修正循环频率误差，根据式对观测信号x(k)进行LCL-FRESH滤波求解最优滤波器系数，得到s1(k)的估计(k);

(5)根据式(12)，利用Schmidt正交化公式从观测信号中消去(k)，以求得另一个源信号，即

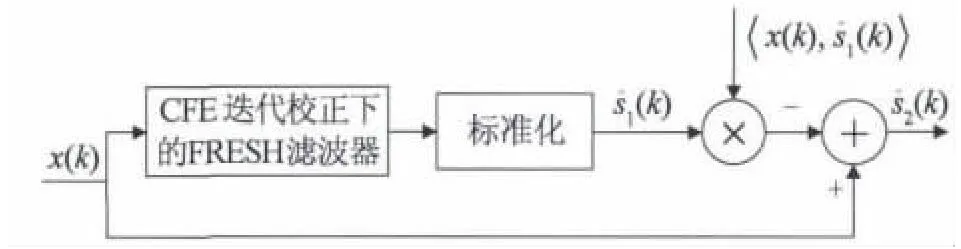
图6 本文算法流程

5 仿真分析

5.1 评价准则

采用式信干比SIR作为评价标准。其中，s(k)表示源信号(k)表示源信号的估计。SIR越大说明估计的信号越接近源信号，估计性能越好，反之，则说明估计的信号与源信号相差越大。

5.2 仿真实验

首先验证本算法用于单通道盲信号分离的有效性，并在不同循环频率误差下进行比较，然后仿真不同循环频率误差对信号分离性能的影响。

仿真实验1:验证本文算法的分离性能

假设 s1(k)是频率为 8.571 MHz、符号速率为3.447 Mbps的BPSK通信信号，s2(k)是频率为12.547 MHz，符号速率为 5.647 MHz的 QPSK 数传信号。LCL-FRESH滤波器阶数取10，非共轭循环频率和共轭循环频率分别取

(1)设置信噪比变化范围为－10～6 dB，分别针对干信比(QPSK信号能量与BPSK信号能量之比定义为干信比)为0、2、4、7 dB时，仿真不同信噪比条件下LCL-FRESH滤波的分离性能，蒙特卡洛仿真次数为50。

(2)设置信噪比变化范围为－10～6 dB，针对干信比为0 dB时，仿真不同信噪比条件下LCLFRESH滤波的分离性能和传统最小均方误差维纳滤波器的比较，蒙特卡洛仿真次数为50。

BPSK通信信号和QPSK数传信号功率谱，如图7所示，图7(a)为BPSK信号和QPSK信号的功率谱，图7(b)为混合后信号的功率谱，可以看出此时两个信号在时域完全重叠，频域上主瓣部分重叠，此时传统的维纳滤波方法已无法实现有用信号的提取和干扰抑制，进而无法进行后续的解调数据处理;不同信噪比条件下LCL-FRESH滤波的分离性能，如图8所示。从图8中可以看出，随着信噪比的增大，系统的信干比输出增大，分离效果越好。

图7 BPSK通信信号和QPSK数传信号功率谱

图8 FRESH滤波分离效果随信噪比变化的结果

所研究的LCL-FRESH滤波与传统维纳滤波在不同信噪比条件下的分离性能，如图9所示。从图9中可以看出LCL-FRESH滤波可以在频谱重叠的条件下(循环频域未重叠)实现信号分离，相比维纳滤波，在较高信噪比的情况下，输出BPSK信号的信干比提高了8 dB以上;LCL-FRESH滤波后的BPSK信号和Schmidt正交化对消后的QPSK信号的功率谱，如图10图示。由图10可以看出本算法可有效地从混合信号中分离出源信号，并且保持源信号的原有特征，进而进行后续的信号处理。该仿真实验验证了LCL-FRESH滤波算法的有效性，可将时频混叠的信号(循环频率互素的源信号)进行分离。

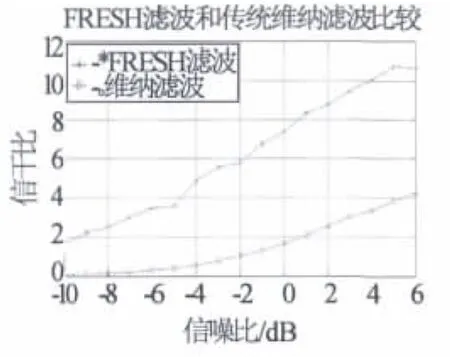
图9 FRESH滤波与维纳滤波比较

图10 分离后BPSK和QPSK信号的功率谱

仿真实验2:不同循环频率误差对分离效果的影响及与现有算法的比较。

(1)仿真场景设置同实验1。为了比较不同循环频率误差对分离效果的影响，分别采用下列不同的循环频率误差，这里考虑的是相对误差(相对载频的误差ΔF/fc后面不在强调循环频率误差均是指相对误差)，在信噪比变化范围为－10 dB～6 dB条件下，进行校正和未校正的仿真分析:

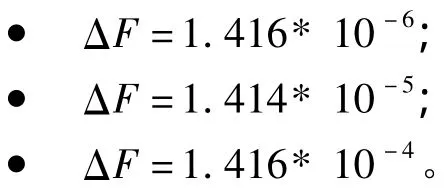
不同循环频率误差下，系统信干比输出情况，如图11所示。结果显示，循环频率误差越大，信噪比越低，LCL-FRESH滤波器的性能越差，当循环频率相对误差大于1.414*10－5时，即使在较高信噪比处已经不具有分离性能，在循环频率误差为1.414*10－4时，输出信干比仅有5 dB，和无误差的情况相比，输出信干比低了将近8 dB，这已经无法进行后期的信号处理、参数估计。采用本文的校正算法后的FRESH滤波信干比，如图12所示。相比未校正前的FRESH滤波器信干比输出在 ΔF=1.416*10－4提高了4 dB，达到10 dB输出。验证了本文算法的有效性。与此同时本文还针对较大的循环频率误差进行了仿真，仿真效果发现，较大的误差下本文的校正迭代算法不再适应，系统信干比输出改善不再这么明显，也是后文需要继续研究改进的地方。

(2)仿真场景设置同实验1。仿真分析典型信噪比和典型干信比条件下，循环频率误差对分离效果的影响，并与现有文献的校正滤波算法进行算法对比。实验中采用典型干信比为0 dB，信噪比为10 dB，循环频率误差(相对载频频率误差)为［1.65*10－6，1.65*10－5，1.65*10－4，2.65*10－4，3.65*10－4，1.65*10－3，1.65*10－2，1.65*10－1，0.5］，这里考虑的是相对误差(相对载频的误差)，采用典型干信比0 dB，蒙特卡洛仿真次数为50，仿真分析如图13所示。

图11 不同循环频率误差下分离效果的影响

图12 不同循环频率误差校正后分离效果的影响

图13 典型条件下不同循环频率误差校正后分离效果的影响

仿真结果更加明显的表明本算法在一定的循环频率误差(相对误差小于10－4)条件下，和现有的算法相比改善信干比输出将近2 dB，和未校正误差时相比改善信干比输出将近4 dB，但是当循环频率误差(相对)大于10－3时，本算法虽然较现有算法有更好的校正效果，但是系统信干比输出也在急剧恶化，LCL-FRESH滤波不在适应系统输出。由此，本算法是以MSE作为代价函数，通过修改最陡下降方向，提出的一种CFE的自适应校正方法，充分利用了观测样本数据，以全部的输入样点对MSE进行训练，使每次迭代误差的变化完全是由CFE的改变而引起，减少了噪声以及干扰源的误差引起的MSE输出变化，并且通过仿真分析表明较传统的校正算法能够有2 dB的信干比输出改善，但是当循环频率误差过大，仿真结果表明循环频率误差大于10－3时，校正算法失效，这是因为循环频率误差过大，迭代算法的代价函数只是针对误差较小的情况下提出的，不再适应大误差条件下的校正，需要寻找更加新的代价函数进行迭代运算，进而校正循环频率误差，这也是后续文章需要研究的地方。

6 结语

研究了在循环频率误差条件下循环频域最优滤波器(频移滤波器)的单通道通信数传信号盲分离的可行性，提出了一种CFE条件下基于循环频域LCL-FRESH滤波和Schmidt正交化对消的信号分离算法。在存在CFE误差的条件下利用LCL-FRESH滤波提取有先验信息的一个源信号之后，通过Schmidt正交化对消法从观测信号中提取出剩余的源信号。仿真结果表明，在各个源信号循环频率互素的情况下，LCL-FRESH滤波可以在存在CFE的条件下进行迭代校正，能够有效实现单通道时频重叠信号的分离，其分离效果明显优于传统的基于最小方差的维纳滤波法。此外，分离出的的源信号利用Schmidt正交化对消方法可以获取另外一个源信号，因此本文仅利用观测信号和已经提取的源信号，就能实现混合系数和剩余源信号的估计，进而进行后续的信号处理。

［1］ JAMES R H，PETER J W RAYNER.Single Channel Nonstationary Stochastic Signal Separation Using Linear Time-Varying Filters［J］.IEEE Transactions on Signal Processing，2003，51(7):1739-1752.

［2］ GARDNER W A.Cyclic Wiener Filtering:Theory and Method［J］.IEEE Transaction on Communications，1993，41(1):151-163.

［3］ 魏安全，沈连丰.CFE下FRESH滤波器性能分析及CFE 校正［J］.电子与信息学报，2008，30(4):853-858.

［4］ GELLI G，LAURA L，AND TULINO A M.Cyclostationaryity-Based Filtering for Narrowband Interference Suppression in Direct-Sequence Spread-Spectrum Systems［J］.IEEE Journal on Selected Areas in Communication，1998，16(9):1747-1755.

［5］ GARDNER W A，NAPOLITANO A，PAURA L.Cyclostationarity:Half a Century of Research［J］.Signal processing，2006，86:639-697.

［6］ 黄知涛，周一宇，姜文利.循环平稳信号处理与应用［M］.北京:科学出版社，2006.

［7］ 王翔，黄知涛，周一宇.基于循环频域滤波及Schmidt正交对消的单通道信号分离算法［J］.国防科学技术大学学报，2012，34(4):120-126.