基于“间隙-接受”的环岛十字交叉口优化模型研究

舒世昌SHU Shi-chang

（湖南交通职业技术学院，长沙 410132）

（Hunan Communication Po1ytechnic，Changsha 410132，China）

0 引言

在无信号灯控制的交通环岛中，车流进入环岛后通过逆时针绕行的方式达到目标出口，因此环形交叉口环岛内可以有效避免车流交织，存在的只是穿插冲突。环形交叉口具有很明显的主支路特征，当环内车流与进环车流相交时，环内车流有先行权，只有当环内的车流出现较大间隙时，进入环的车辆才能进入交叉口。因此以间隙-接受理论为基础，分析在各种道路和交通条件下进环车辆的通行能力是目前普遍采用的方法。间隙-接受理论中，最重要的一种方法就是运用概率论和排队论来推导环形交叉口的通行能力。

“间隙-接受”是指当环道上的车流出现大于某一临界间隙tc（s）时，进环车辆才能进入，否则就必须等待，而环内车辆可以直接经过环形交叉口内的冲突区而不受延误。环形交叉口的通行能力的间隙-接受理论模型可以从两股交通流相互作用时的排队模型中推导出来。由于在环形交叉口环形车道上车辆一般无超车行为，当交通量较小的时候，属于自由流状态时，车头时距服从负指数分布或移位负指数分布。当交通量较大、车辆跟驰行驶时，其非随机性大大增加，车辆之间的车头时距不再服从负指数分布，对这种状况描述车头时距更适合Er1ang分布。

在以间隙-接受理论建立的交通环岛模型中，通常以进口车道能进入环形交叉口的最大流量反映环形交叉口的通行能力。

1 交通环岛间隙-接受模型

间隙-接受概念是指当环行车流出现大于某一临界tc（s）间隙时，进环车辆才能进入，否则就必须等待，而环行车辆可以直接经过交叉口内的冲突区而不受延误。

环形交叉口的间隙-接受理论模型可从两股交通流相互作用时的排队模型中推导出来。由于环行车道上车辆几乎不会发生超车行为，可认为环行车辆的车头时距服从移位负指数分布。当环行车道车流量较大时，部分环行车流会以最小行车时距tm(s)结队行驶。设α表示车头时距大于tm的车流的比例，环行车流量为q(pcu/s)，环行车流的车头时距大于和等于tm的概率应分别为各车流所占比例，即α和1-α，（通用公式中α=10故环行车流的车头时距有如下的概率分布密度：f(t)=αλe-λ（t-tm）（t＞tm），。设tf(s)为进环车流的随车时距，即当环行车道上车流的车头时距较大，允许两辆以上汽车进入时，进口车道上排队进入环形交叉口时相邻两车的车头时距。

当 tc＜h＜tc+tf时，允许一辆汽车进入交叉口；当 tc+(k-1)tf＜h＜tc+ktf时，允许k辆车进入交叉口。设环行车流出现tc+(k-1)tf＜h＜tc+ktf的概率为pk，则pk=p（h≥tc+(k-1)t）f-p（h≥tc+kt）f=αe-λ（tc+(k-1)tf-tm）-αe-λ（tc+ktf-tm），设每小时能够进入环行车道的车辆数为Cn，则得到计算公式如下：

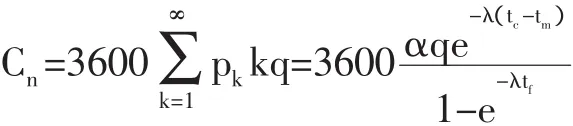
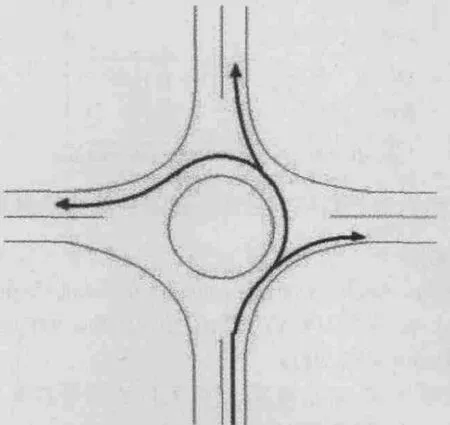
图1 交通环岛示意图

2 环岛通过能力计算

以一个普通的城市环形交叉口为例细化模型，假设进车道为3车道（左、直、右），而环道为两车道。环形交叉口的进口车道上右转车辆不进入环车道，即右转弯车辆不参与穿插冲突。环形交叉口的两条进口车道(左、直)进入交叉口时，左侧的左转弯车流需与两条环形车流穿插才能通过环形交叉口，而相对处于右侧的直行车流只需与外侧的环形车流穿插就可以通过环形交叉口。设CN1、CN2和CN3为左、直、右3条车道进入环形交叉口的车辆数，则环形交叉口总的通行能力为CN=Cn1+Cn2+Cn3。

对于右转车流，由于交通渠化程度较高，环形交叉口的进口车道的右转弯车辆不经过冲突的区域，即不参与穿插冲突，所以其通行能力相当于一条右转专用车道的通行能力。原则上可按直行方法计算，将直行的通过时间换算成右转的通过时间，计算公式为

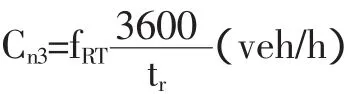
对于直行车流，当直行车流进入环形交叉口时，它只需要与环道的外侧车流进行穿插就可以通过环形交叉口，只有当环道外侧车道上的车辆之间的车头时距超过临界间隙tc时方能进入交叉口，否则，必须等待。当环形交叉口进口车道上有车辆排队时，当环道上车流的车头时距较大时，可允许2veh以上的汽车进入。假设环形外侧车道车流车头时距hout服从r阶Er1ang分布，外侧车道车流的流率为λ/r（veh/s）。下面计算g秒内允许多少辆入环的车辆驶过环形交叉口外侧车道上的冲突区C点[6]。

当 tc＜hout＜tc+tf时，允许汽车 1 veh 进入；当 tc+（k-1）tf＜hout＜tc+ktf时，允许汽车k veh/s进入环形交叉口的外侧车道。设环形车流出现 tc+（k-1）tf＜hout＜tc+ktf的概率为 pk，则

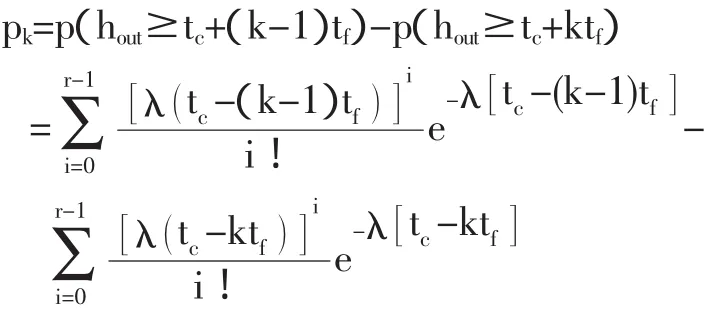
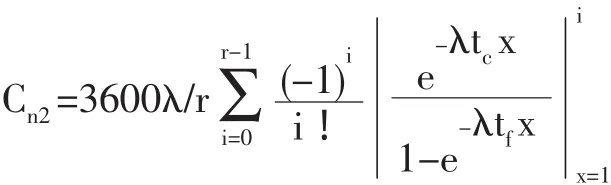
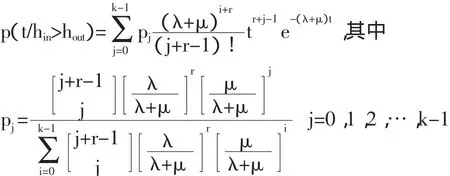
对于左转车流，当左转车道车辆进入环形交叉口时，需与环道上两条环形车流穿插才能进入交叉口。假设环形交叉口内侧车流车头时距hin服从k阶Er1ang分布，车流率为 μ/k（veh/s）。当 tc＜hout＜tc+tf时，此时左转的 1 辆车只能进入环形交叉口外侧车道，与此同时，只有hin＞hout条件也成立时，左转车流才可以进入内侧环道。假设hin、hout独立，这样本文的问题就转化为hin＞hout的条件概率分布的问题。根据混合型双参数加法定理，在hin＞hout条件下，hout的条件分布是 k 个参数（j+r，λ+μ）的 Er1ang分布混合，j=0，1，…，k-1，条件密度为

这样就相当于外侧车头服从上述的分布，即按照条件概率分布，只要能通过外侧的环形车道，车辆就可以通过内侧车道的冲突区域，可得出左侧车道的通行能力为

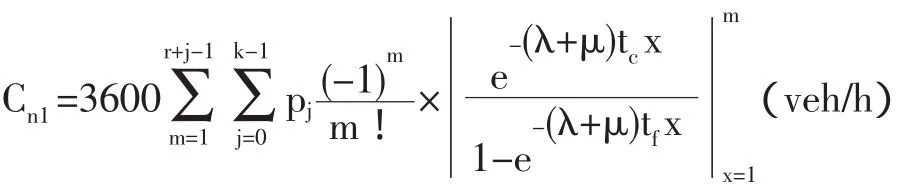
根据以上所求的3条车道的通行能力，可得到双环行车道逆时针环流通行能力CN为

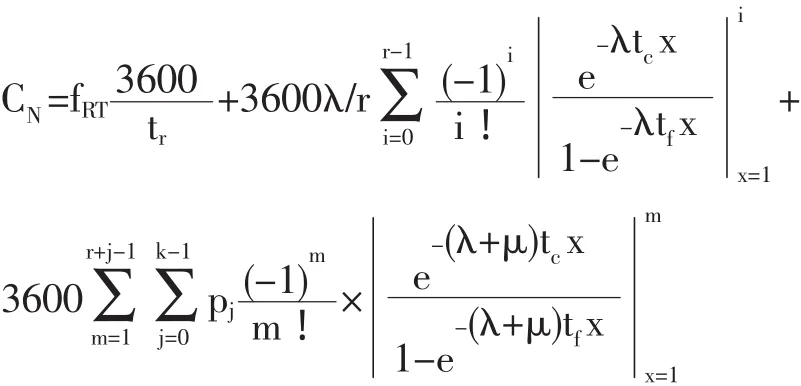
3 模型分析

根据以上建立的交通环岛“间隙-接受”数学模型，分析了环岛路口的间隙-接受通过能力与交通流大小的关系。根据以上的推导，在某一个时刻一个简单的单车道环岛接受车流与环岛内车流量的关系如图2。

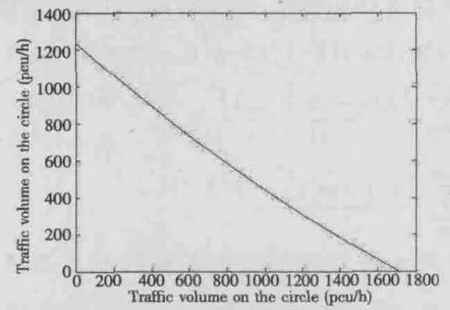
图2 环岛内车流密度与“间隙-接受”能力示意图

而某一时刻环内车流量由上一时刻各入口来车流量决定，在一个平衡，各个方向O-D均匀，连续的模型中，环岛内车流量为每个入口来车流量的两倍。此时整个交通环岛的流通能力达到最大值。

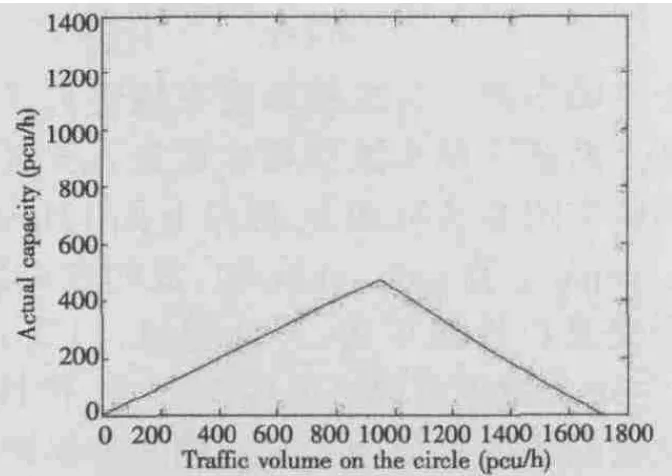
图3 均衡状态下环岛通过能力示意图

将模型扩展到多车道的情况下，可以得到同样的分析结果（图 4、图 5）。

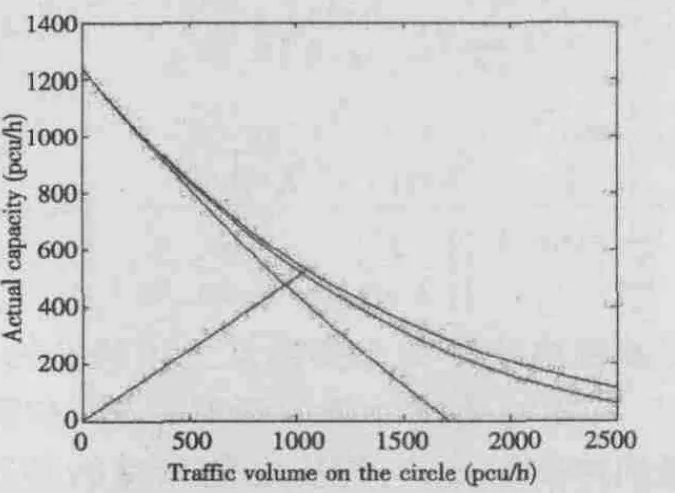
图4 入口单车道情况下环岛内1，2，3车道时通过能力示意图

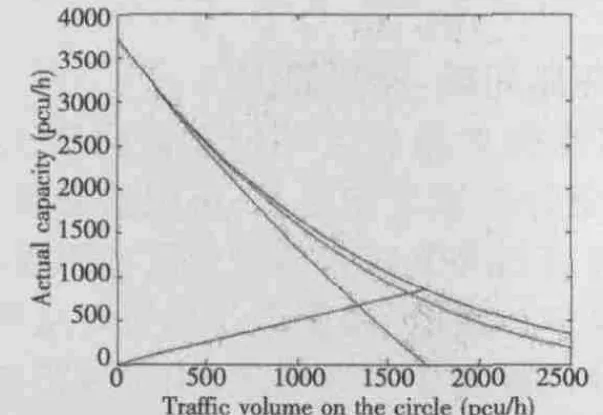
图5 入口多车道情况下环岛内1，2，3车道时通过能力示意图

可见，当车流量越小的时候，交通环岛具有越大的通过能力，随着车流量加大，造成环岛内车流密度增加，环岛的“间隙-接受”能力能力将会减少，当超过临界值的时候，通过能力就会下降，造成交通拥堵。在无信号灯控制的交通环岛组织管理形式下，即便扩大环岛建设规模，增加环岛内车道数，但是受限于“间歇-接受”能力，边际效用会越来越小。而一旦当车流量超过临界值，大量车流拥堵在交通环岛内，进一步造成能力下降，故而将引发拥堵。

4 交通环岛组织与管理优化方法

为了解决交通环岛拥堵问题，根据以上研究，为了缓解交通环岛拥堵，增加交通环岛通过能力，可以进行以下组织与管理方法的优化：

①在环岛入口处进行车道改造，由于通过交叉路口环岛时车流速度较慢，可将行驶车道宽度减小，车道数增加。②扩建环岛，增加环岛内车道数。③使用信号灯控制进入环岛的车流量，保持环岛的最大通过能力。

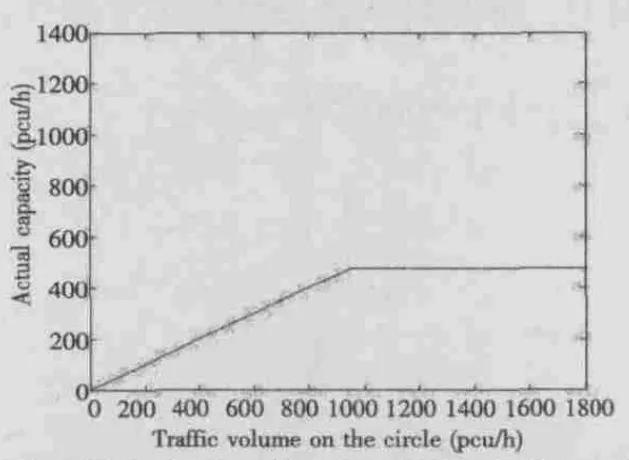
图6 引入信号灯控制后的环岛通过能力示意图

[1]Zhengke.Ana1ysis of the capacity of roundabout with signa1.The Journa1 of HIGHWAY ENGINEERING OF CENTRALSOUTH CHINA vo125,2000.

[2]刘会斌,邓卫,李东屹.环形交叉口的信号控制方法研究[J].道路交通与安全，2008(02).

[3]Bri1on,W.;Bondzio,L.;Wu,N.,Unsigna1ized Intersections in Germany-a State of the Art,2nd Internationa1 Symposium for Unsigna1ized Intersections,Port1and/Oregon,1997.

[4]Tanner,J.C.,The capacity of an uncontro11ed intersection.Biometrica,54(3 and 4),pp.657-6581967.

[5]陈晓明.混合交通条件下城市道路信号交叉口通行能力理论研究[D].北京交通大学，2008.

[6]Stuwe,B.Untersuchung der Leistungsfaehigkeit und Verkehrssicherheit an deutschen Kreisverkehrsp1aetzen. (Investigation of capacity and safety at German roundabouts),Pub1ication of the Institute for Transportation and Traffic Engineering at the Ruhr-University Bochum.No.10,1992.

[7]廖铄澔,刘怡杉.交通环岛优化模型设计及应用[J].交通标准化，2010(15).

[8]Hunan communication Bereau,http://www.hnjt.gov.cn/,2-9-2009.