数学规划在测绘工作中的应用

于祖国YU Zu-guo

（昆明理工大学国土资源学院，昆明 650000）

（Facu1ty of Land Resources Engineering，Kunming University of Science and Techno1ogy，Kunming 650000，China）

0 引言

测绘是国民经济建设和发展的重要基础性前期工作。随着经济的发展，现代测绘的生产规模日益扩大，分工越来越细，要求测绘生产组织必须具有高度计划性。将数学规划的方法运用于测绘工作中，对测绘工作实施过程中各种错综复杂的数量关系进行研究，并归结成一定的数学模型，用数学方法找到最合理的工作方案，在保证工程要求和精度要求的前提下，可以达到提高工作效率，减少生产消耗的人力、物力、财力的目的。

1 线性规划的应用

在测绘经营管理中，经常要解决两类问题：一类是对于某项确定的生产任务，如何使用最少的资源，保质保量的完成测绘任务；另一类是对于有限的资源，如何安排使其最大限度的发挥作用，取得更多的测绘成果。对于这些问题，都可以应用线性规划的方法，通过建立数字模型、求解、应用，科学合理地解决。这里以一例说明线性规划问题在测绘工作中的应用。

现有某测绘单位为下月生产计划做安排，该测绘单位计划安排建筑物放线、1:500竣工测量两种种测绘工作。已知该测绘单位生产的定额为：建筑物放线每件需要外业2工天，内业3工天，检查1天；1:500竣工测量每幅需要外业6工天，内业5工天，检查2工天。而该单位下月总得生产能力为：外业生产240工天，内业生产220工天，生产检查90工天。建筑物放线测绘获利为720元/件，1:500竣工测量为1600元/幅。那么该测绘单位应如何安排测绘工作以使收益最大？

在本问题中，根据已有条件可以设：下月进行建筑物放线x1件，1:500竣工测量x2件，根据线性规划的理论，可以建立模型。

则希望获得的最大产值的目标函数为：

约束条件为：

在上述数学模型中加入松弛变量，得到以下标准形式：Max z'=720x1+1600x2

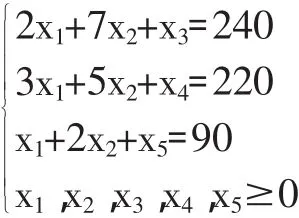
用单纯形法求出上述问题的最优解，得到最终表为：

表1

通过单纯形表可以求出此线性规划问题的最优解，即建筑物放线15件，1:500竣工测量35幅。

最大收益为 max z=15×720+35×1600=66800（元）

2 人工变量法

在实际测绘工作中，并不是所有的时候都如上述问题一样，约束条件都是“≤”式，而有可能出现“≥”式或“=”式，这是很有可能的。当约束条件是“≥”式或“=”式时，将建立的线性规划模型的一般形式化为标准形式后，约束条件系数矩阵中就不包含有单位矩阵。这种情况下我们需要使用人工变量法，通过加入人工变量的方式，人为的构造一个单位矩阵来求解问题。这里我们通过大M法求解。

依然沿用线性规划中的例子，如果根据实际工作情况，要求内业工天不小于为220工天，检查工天恰好为90工天，此时应如何安排工作使收益最大。

此问题的数学模型就变成

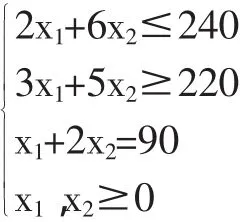
在约束条件中分别加入松弛变量x4、剩余变量x5、人工变量 x6、x7，得到 Max z=720x1+1600x2+0x3+0x4-Mx5-Mx6

这里M是一个任意大的正数。

通过单纯形法可以求出此线性规划问题的最优解，即建筑物放线30件，1:500竣工测量30幅。

最大收益为 max z=30×720+30×1600=69600（元）

3 灵敏度分析

当线性规划的系数aij、bi、cj发生变化时，最优解也可能会随之发生变化。虽然通过重新使用线性规划的单纯形法能够求解，但是这样既麻烦又没有必要。通过灵敏度分析的方法则可以比较方便的求出这些参数的变化对最优解的影响。

3.1 技术系数aij的变化 在实际的测绘工作中，由于生产规范、人员变动、技术发展乃至天气变化等等因素，都可能导致技术系数aij发生变化。依然沿用上例，但是由于测量工作要求，生产时间发生变化，现在放线需要外业2工天，内业2工天，检查1工天。此时就是技术系数aij发生了变化。应如何安排工作。

代入表1，并通过单纯形法计算，可得x1=30，x2=30。说明当技术系数发生变化时，最优解也随之发生变化。

3.2 资源系数bi变化 在实际测绘工作中，在根据问题建立数学模型时，若将生产能力、仪器、设备等等视作资源，那么当这些资源发生变化，例如新购置一批仪器、增加了新的工作人员等等时，资源系数会发生变化。仍以上例为例，假设由于该测绘单位生产能力增加。现总的外业工天增加40工天，内业工天增加40工天，检查工天增加20工天。此时显然资源系数bi发生了变化。那么应如何安排工作。

②计算Δb'和b'+Δb'

由于b'+Δb'≥0，原最优解仍为最优解。否则用对偶单纯形法迭代。这里最大收益为即建筑物放线20件，1:500竣工测量40幅。

3.3 价值系数cj变化 由于市场条件是在不断变化的，因此在实际工作当中，价值系数cj也是会不断发生变化的，这会对原来的决策变量发生影响。

继续引用前文线性规划中的例子，由于该测绘单位业务拓展，现在可以新增一种线路工程测量工作。已知该工作每千米需要外业5工天，内业3工天，检查2工天。线路工程测量的收益为1200元/千米。显然，此时价值系数cj发生了变化。是否增加该工作？

根据要求，设增加线路工程测量的计划产量为x6，则它的价值系数c6=1200，对应的技术向量P6=(532)T

由于σ6＞0，因此需要按照单纯形法继续迭代。

代入表1并通过单纯形法计算可得，x1=22，x2=26，x6=8，此时收益为 max z=22×720+26×1600+8×1200=67040（元）

显然，此收益是大于之前只安排两项工作时的收益。因此，应该安排线路测量工作。

4 整数规划

在前面的线性规划，目标规划中，求出的最优解都有可能包含小数或分数。而在实际测绘生产工作中，由于人员、仪器设备、控制点个数甚至工时工天都只能是整数而不能使小数或分数。此时如果简单的将求得的最优解进行四舍五入取整，得到的结果可能不符合约束条件，或者即使满足约束条件，却不是最优解。此时，需要通过整数规划的方法进行最优解的求解。

仍以上文中的例子为例，假设由于该测绘单位扩大生产能力，内业工作时间增加了10工天，总共有230工天。

在这种情况下，依据线性规划的理论，利用单纯形法可求得，安排生产22.5件建筑物放线，32.5幅1:500竣工测量时，可获得最大收益68200元。

如果简单的通过四舍五入来取整，即安排建筑物放线23件，1:500竣工33幅，那么它破坏了约束条件，即超出了实际生产能力。为了确定最优方案，这里通过分支定界解法求解。

将要求解的整数规划问题称为问题A，其对应的线性规划问题称为整数B。

可将原问题分解为两个子问题B1、B2（即两支），给每支增加一个约束条件。这并不影响问题A的可行域，不考虑整数条件解问题B1、B2，称此为第一次迭代。

得到最优解如表2所示。

继续对问题B1和B2进行分解，因为z1＞z2，故先分解

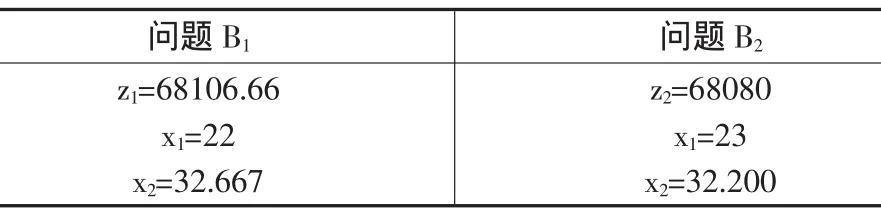
表2

B1为两支。分别增加条件x2≤32和x2≥33，得到问题B3和问题B4，进行第二次迭代，得到最优解如表3所示。

表3

可见，问题B3和问题B4的解都已经是整数解。

而问题B2的目标函数值z2=68080，所以可能在67920≤z*≤68080之间有整数解，因此继续对问题B2进行分解。得到问题B5和B6。（表4）

由于问题B5的目标函数值大于所有的整数解，继续对问题B5进行分解。（表5）

此时可以判断问题B4的解x1=21，x2=33为最优整数解。此时最大收益max Z=z*=67920（元）。

本文以一个实例为基础，分析了线性规划、灵敏度分析、整数规划等数学规划方法在测绘工作中的应用，讨论了如何应用数学规划的方法，对测绘生产工作进行组织安排，以提高生产效率。除此以外，数学规划在测绘工作中还可以有其他更多的应用，由于篇幅有限，本文不一一讨论了。

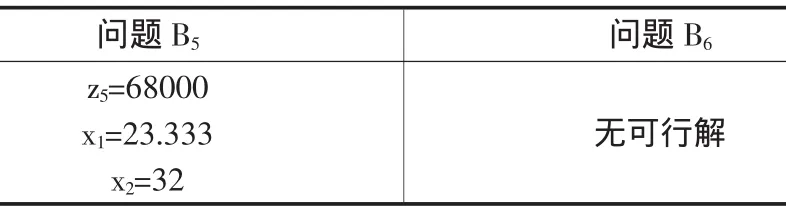
表4

表5

[1]甘应爱等.运筹学（第三版）[M].清华大学出版社，2005（6）.

[2]郑肇葆等.数学规划在测绘运筹学中应用（第二版）[M].测绘出版社，2003.

[3]龚强.测绘运筹学导论[J].东北测绘，1998，21(3).

[4]龚强.略论测绘运筹学模型及建模基本原则[J].黑龙江测绘，1997，20(1).