流域水循环系统多维调控方案的评价与优选

徐 凯，汪 林，甘治国，季海萍

(中国水利水电科学研究院流域水循环模拟与调控国家重点实验室，北京 100038)

自然状态下，流域水循环系统具有资源与生态属性。随着人口的增长与经济社会的发展，水循环系统呈现出明显的“自然—社会”二元特性［1］。水循环过程发生改变，系统衍生出社会、经济与环境属性，并导致原有的资源属性削弱、生态属性衰退［2］。探究水资源合理高效利用模式，引导水循环系统良性发展，保障水资源可持续开发利用，是当前水资源研究的热点问题［3］。流域水循环系统多维调控是促使水循环系统五维(资源、经济、社会、生态、环境)属性协同演化的有效手段［4］。合理准确的调控方案评价与优选方法，对获取较优的调控方案至关重要。有关调控方案评价与优选方法的研究很多，Chen等［5］将模糊理论应用于Tseng-Wen和Kao-Ping River流域水资源调配方案评价与决策制定;Srdjevic等［6］将流域模拟与调控方案评价技术相结合 利用基于熵权的 法评价 流域调控方案 等 综合了水文模型 水库调度模型与流域需水预测模型，以流域水资源短缺量为指标评价了Pinios River与Lake Karla流域水资源管理措施;Lahloh等［8］利用遗传算法对水污染修复措施进行优化引导，完成对措施方案的优选;吴泽宁等［9］提出了流域可持续发展评价准则，利用人工神经网络模型评价水资源利用效果;Okeola等［10］基于层次分析法(AHP)的多重决策分析理论，对尼日利亚Kwara州城市供水方案进行评价，指出公共持有与管理是最适宜的供水策略;贾仰文等［11］采用GDP、粮食产量等7项评价指标对海河流域多维调控情景方案进行了定量评价与优选;丁勇等［12］将D-S证据理论方法应用于多水库联合调度方案评价，通过融合不确定性信息，获取方案评价的确定性指标;Gan等［13］等采用有序度熵对流域多维调控方案进行评价与优选，并应用于海河流域多维调控方案评价。

上述方法主要针对某一水平年的方案进行评价与优选，对各水平年推荐方案则按时间组合得到跨水平年系列组合调控方案。有研究表明:调控方案简单组合得到的结果未必是最优的。基于线性理论的叠加方法得到调控方案存在一定不足［14］，原因在于水循环系统本身是非线性的，对社会经济发展的影响与响应也是非线性的。本研究基于熵理论与协同学理论，以系统协调度与有序度综合距离对单一水平年方案和跨水平年组合方案进行评价与优选，充分考虑时间因素对水循环系统多维调控的影响，以海河流域为例，验证本调控方案评价方法的合理性、可行性。

水循环系统多维调控的目标是调整系统五维属性间的竞争协同作用，实现系统整体有序演化，这与协同学的研究目标一致，因此，将协同学理论应用于水循环系统多维调控是可行的［15］。协同学理论认为系统性质的改变源于各子系统的协同作用，而子系统的有序程度可利用序参量的协调度来反映［16］。本研究基于协同学理论，引入协调度来量化系统要素间的协同作用，强调时间因素，利用有序度综合距离反映跨水平年组合调控方案中水循环系统与期望状态的接近程度。

1 流域多维调控方案的评价

1.1 建立有序度函数

序参量是子系统发展演化的控制因素，协调作用状态影响到子系统的有序程度。现实中，水资源开发受到多种因素限制，序参量取值只能分布在一定范围内。序参量有序度计算公式为

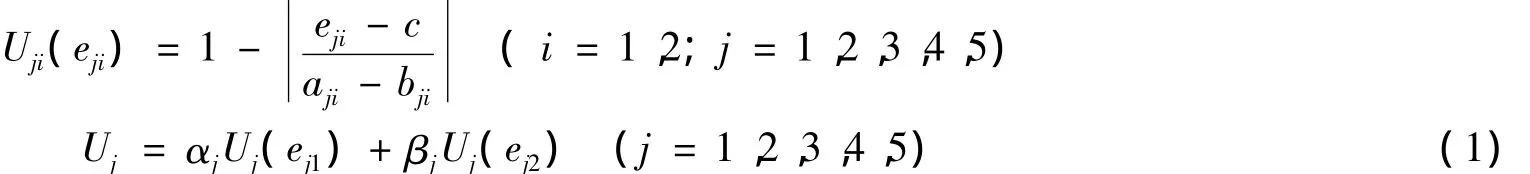
式中:Uji(eji)—— 第j维属性第i个序参量有序度;eji—— 第j维属性第i个序参量取值;aji、bji——eji可取的最大值、最小值;c——eji取值范围内的期望值，c∈［aji，bji］，可基于水循环系统整体协调的期望情景确定;Uj—— 各维属性有序度;αj、βj—— 第j维属性序参量的权重。

根据公式，若eji取值在可行阈值范围［aji，bji］内，有序度Uji(eji)∈［0，1］，取值越接近c，Uji(eji)越接近1。

1.2 系统协调度函数的建立与单一水平年方案的评价

调控方案的评价与比选标准是水循环系统的整体协调程度，因此选取系统协调度作为调控方案评价指标。利用几何平均法，确定系统协调度计算公式为

式中:H(t)——系统协调度;θ—— 参数，保证系统每一维属性有序度均为正时，系统协调度才为正。

系统协调度H(t)∈［-1，1］。针对某一特定时间段t，水循环系统的H(t)越大，五维属性越协调，单一调控方案的效果越好。

1.3 有序度综合距离函数的建立和跨水平年组合方案的评价

当调控方案涉及多个水平年时，各水平年都有相应的系统协调度H(t)，缺少一个综合指标来评价跨水平年组合方案效果。本研究引入有序度综合距离指标解决跨水平年组合方案的评价比选问题。有序度综合距离是指调控跨水平年组合方案后 水循环系统的实际状况与期望状态的差距

假设组合方案涉及N个水平年，有序度综合距离计算公式为

式中:ρ——跨水平年组合方案的有序度综合距离;Un，j—— 第n个调控时段水循环系统第j维属性的有序度。

根据定义，ρ越小，水循环系统整体越趋近于期望状态，跨水平年组合调控方案的效果越好。

流域多维调控方案评价流程见图1。

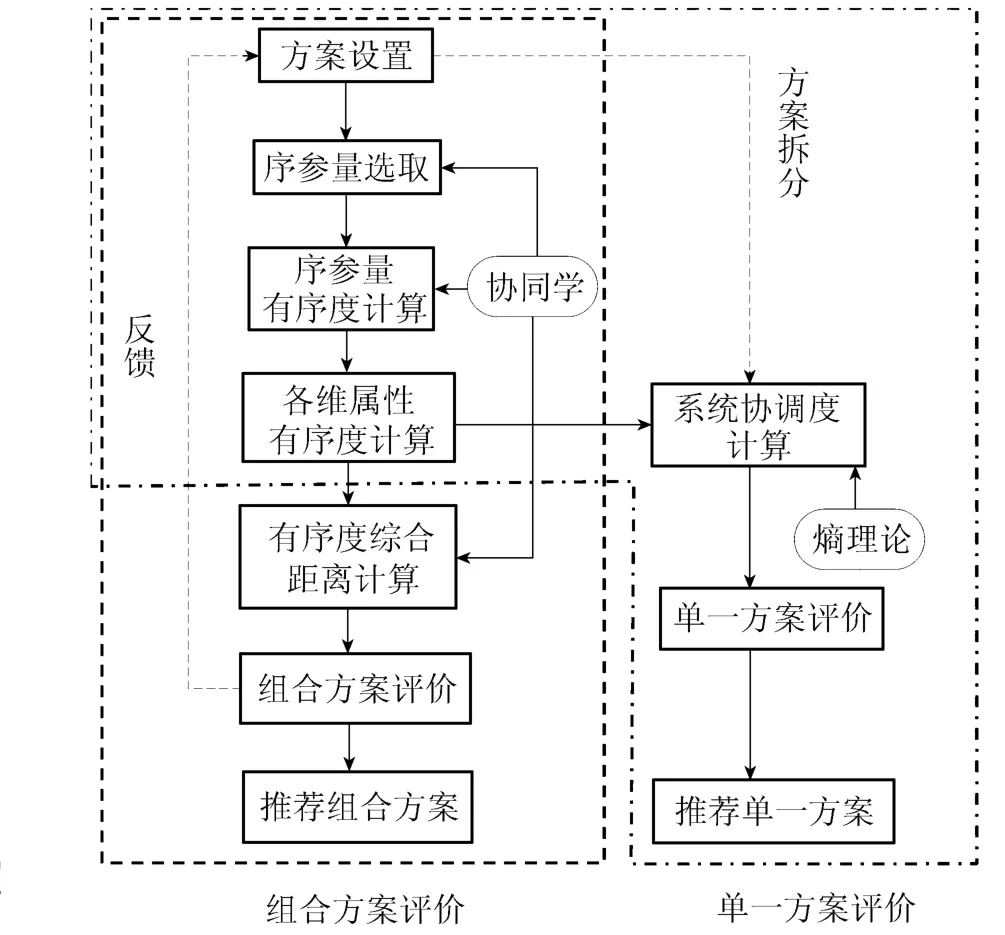
图1 流域多维调控方案评价流程Fig.1 Process of scenario evaluation for multidimensional regulation

2 流域多维调控方案评价方法的应用

2.1 研究区域

海河流域位于华北地区，流域面积约31.8万km2，属半干旱半湿润气候，年降水量较少，且时空分布不均，多年平均降水量539 mm，水资源总量约372亿m3，人均水资源量305 m3，仅为全国人均水资源量(2 151 m3)的 1/7，世界人均水资源量(8549 m3)的1/28，是全国乃至全世界水资源供需矛盾最尖锐的地区之一。评价与优选海河流域多维调控方案，对指导流域水循环多维调控有重要实践意义。

2.2 调控方案的设置和评价指标的建立

根据一定的水文条件(降雨、径流等)设置多维调控方案。以海河流域1956—2000年系列水文条件为基础，2007年为基准年，进行不同水平年边界条件(调水量、地下水超采量等)情景组合。选取其中7个情景组合方案(表1)说明本研究所用评价方法的有效性。

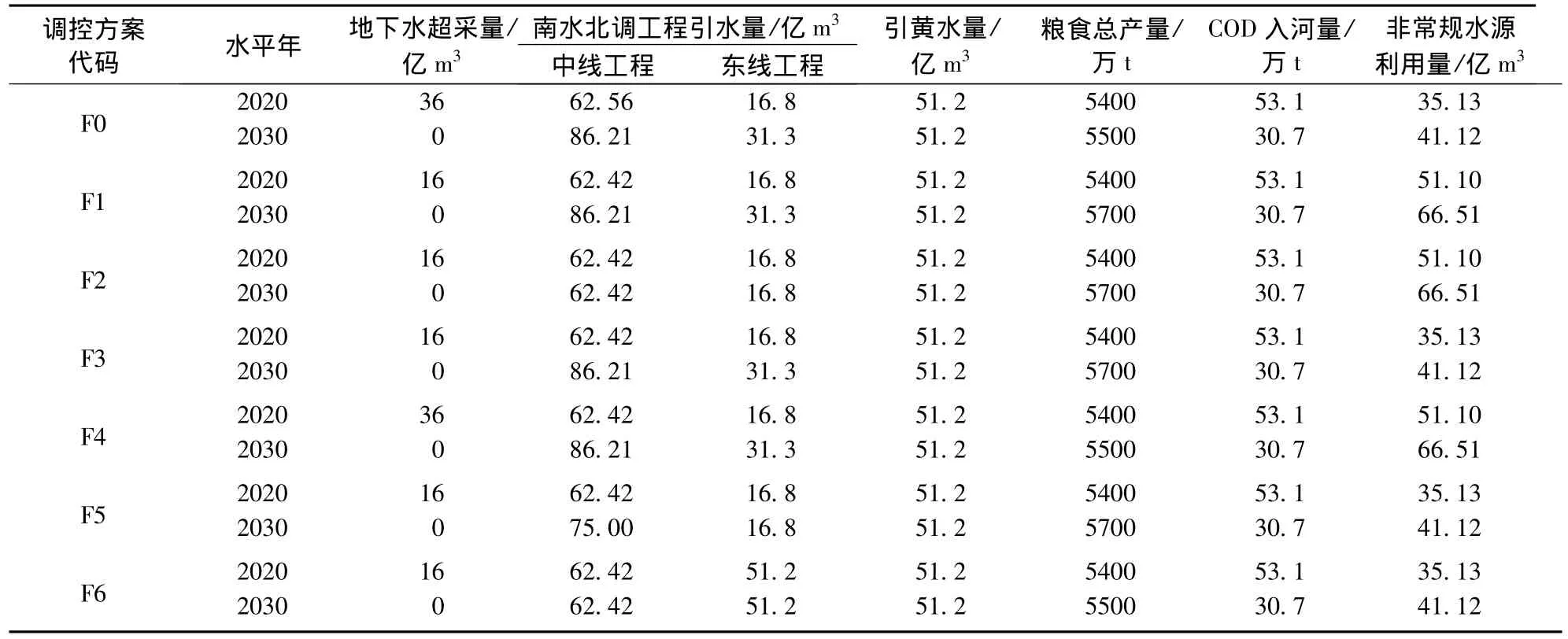
表1 调控方案的设置Table 1 Settings of regulation scenarios

考虑海河流域水资源开发利用特点及生态环境特性，确定10项调控方案评价指标(序参量)。资源维属性考虑水循环稳定和可再生性维持，选用地表水开发利用率和地下水超采量为主要评价指标;经济维属性以人均GDP和万元GDP用水量为评价指标，来反映经济发展水平和水资源利用效率;社会维属性以保障粮食生产安全与社会公平稳定为主要目标，选用人均粮食产量和人均生活用水比(农村/城镇)为评价指标;生态维属性以入海水量与河道生态用水量为指标，表征生态环境用水满足程度;环境维属性要求污染物排放达标 因此以 入河量和水功能区达标率为指标 从正反两方面反映水环境质量

利用多目标分析决策模型(DAMOS)［17］模拟计算各组合方案的调控结果，评价指标(序参量)模拟计算结果见表2。

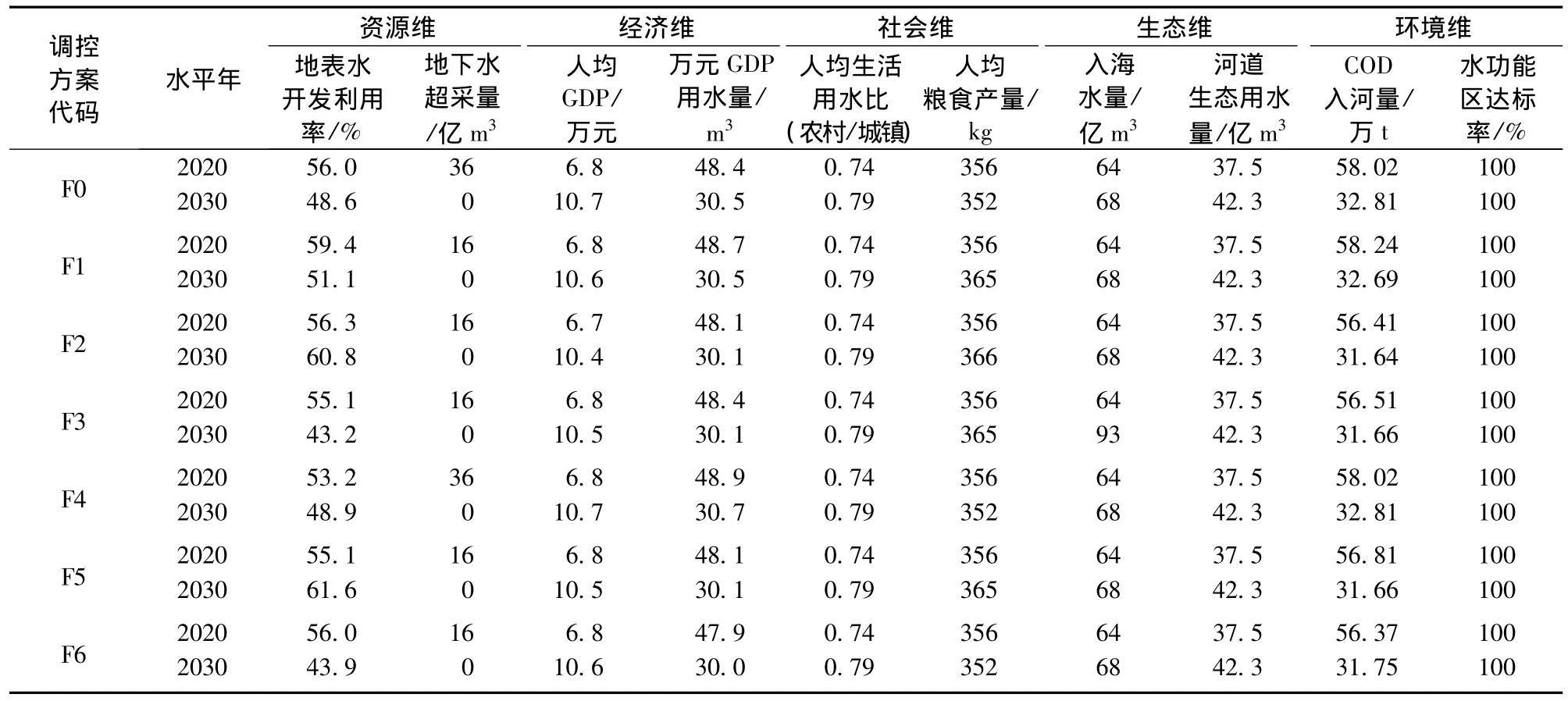
表2 调控方案评价指标模拟计算结果Table 2 Calculation results of evaluation indices of regulation scenarios

2.3 方案评价

2.3.1 评价指标理想点、阈值及权重的确定

考虑海河流域水循环条件与经济社会发展的基本定位，结合海河流域水资源综合规划，分析各指标间的相关性，利用交换比［18］等方法，确定评价指标的理想点及阈值，指标权重则采用专家打分法确定，各指标权重分别为:地表水开发利用率0.4，地下水超采量0.6，人均GDP 0.4，万元GDP用水量0.6，人均生活用水比(农村/城镇)0.3，人均粮食产量0.7，入海水量0.4，河道生态用水量0.6，COD入河量0.5，水功能区达标率0.5)。评价指标的理想点、阈值见表3。

表3 评价指标(序参量)的理想点、阈值Table 3 Ideal values，thresholds of evaluation indices(order parameters)

海河流域水资源综合规划给出了河道生态用水量、COD入河量和水功能区达标率的分时段目标，本研究将这些目标值作为评价指标的理想点和阈值。地下水超采量、入海水量、地表水开发利用率、人均粮食产量、人均GDP同国民经济用水量密切相关，基于DAMOS模型的多次模拟结果，采用交换比方法建立这些指标与国民经济用水量的统计关系，并参考海河流域水资源综合规划中的国民经济用水分时段指标，确定这些指标的理想点与阈值。人均GDP、人均粮食产量采用GDP、粮食产量除以海河流域水资源综合规划设定的人口得到。万元GDP用水量指标通过国民经济用水量与GDP的比值来计算。人均生活用水比(农村/城镇)的理想点与阈值则参考海河流域基准年(2007年)城乡人均生活用水定额、规划年(2020年、2030年)人均生活用水定额和流域内发达地区人均生活用水定额来制定。基准年农村与城镇人均生活用水定额的比值约为0.6，北京等发达地区可以达到为0.8，规划年农村人均生活用水定额约为城镇的0.78。

2.3.2 单一方案评价

根据序参量有序度及系统协调度计算公式(1)和(2)，计算水循环系统协调度，结果见表4。

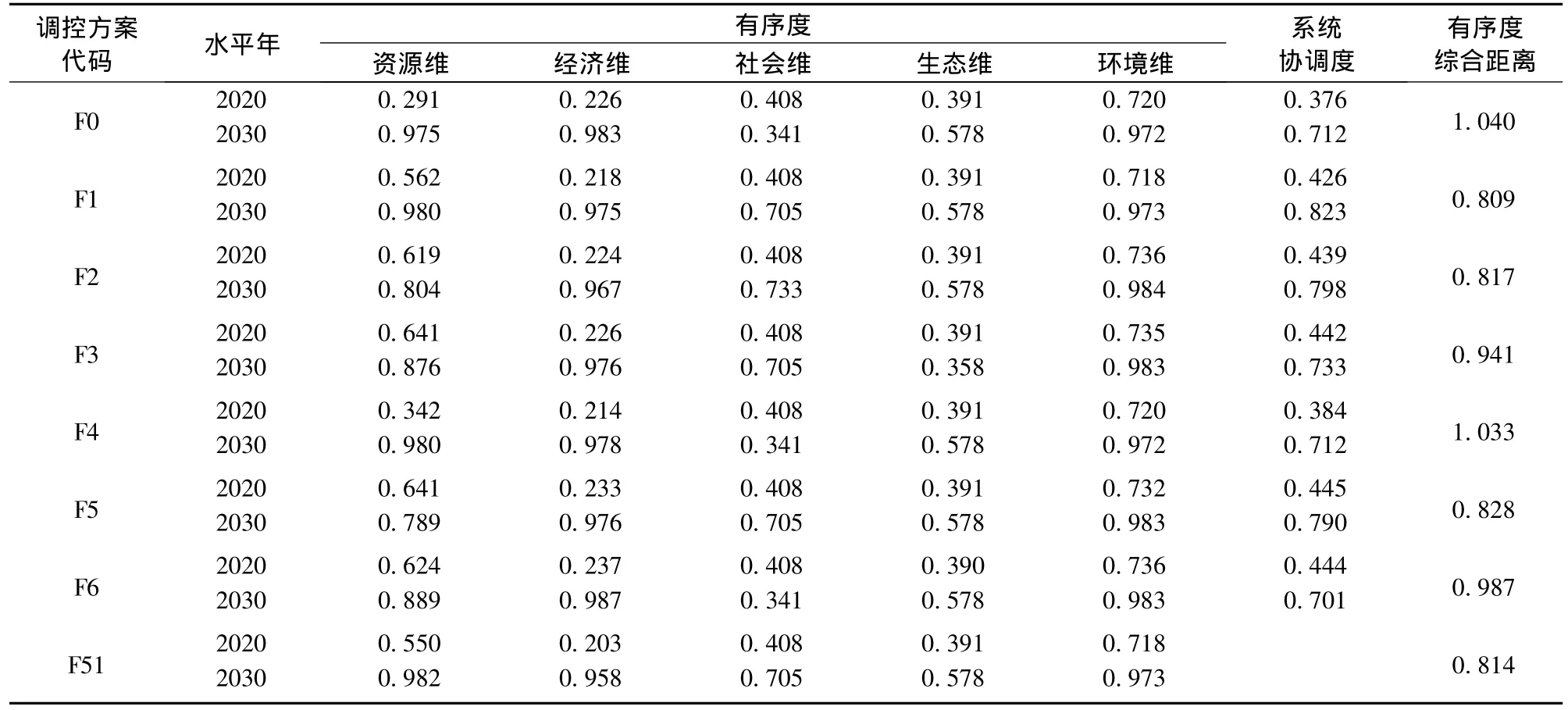
表4 各调控方案的有序度、系统协调度及有序度综合距离Table4 Order degrees，coordination degrees，and integrated distances of order degreesin various regulation scenarios

从表4可知，经过方案调控，海河流域水循环系统协调度均呈增加趋势。水平年2020年F5方案系统协调度最高，2030年F1方案系统协调度最高，说明从单一水平年看，两者的调控措施最有效。

在2020年的调控方案中，F5方案降低了地下水超采量，提高了经济产出，COD入河量略有增加，流域较高的地表水开发利用率得到控制，用水效率提高，因此F5方案的环境维有序度出现一定下降，资源维、经济维的有序度则显著提升;就水循环系统总体而言，其协调度最好。F1方案在2030年增加了调水量与非常规水源利用量，提升了粮食产量与人均GDP，控制了地表水开发利用率，实现生态维、环境维的有序度稳定的前提下，资源维、经济维与社会维的高度有序，系统五维属性协调度最好。

2.3.3 组合方案评价

将系统协调度最高的方案(2020年的F5和2030年的F1)相组合，构成F51方案，并参与调控方案的比选。根据有序度综合距离计算公式，计算各调控方案有序度综合距离，结果见表4。

计算结果表明，在综合考虑2020—2030水平年的多维调控下，F1方案的流域水循环系统最接近期望状态，是8个调控方案中的较优方案。尽管F51是单一水平年系统协调度最高的方案的组合，但F51方案有序度综合距离为0.814，大于F1方案的有序度综合距离0.809，说明F51方案水循环系统的整体协调性不及F1方案。说明非线性条件下，简单叠加方法存在一定的不足。

3 结 语

本研究提出的基于系统论思想的水循环系统多维调控方案的评价与比选方法，充分考虑了时间因素对水循环系统多维调控的影响，较好地比选了海河流域水循环系统多维调控单一方案和组合方案，说明由单一调控方案简单叠加形成的组合调控方案，其调控效果未必是最好的。结论可为其他流域的水循环系统多维调控方案的评价与优选提供参考。

［1］［1］LIU Jiahong，QIN Dayong，WANG Hao，et al. Dualistic water cycle pattern and its evolution in Haihe Ｒiver basin［J］. Chinese Science Bulletin，2010， 55( 16) : 1688-1697.

［2］GAN Hong，WANG Lin，CAO Yinbai， et al. Multi-dimentional overall regulation modes and threshold values for water cycle of the Haihe Ｒiver Basin［J］. Chinese Sciences Bulletin， 2013，58( 27) : 3320-3339.

［王浩，严登华，贾仰文，等. 现代水文水资源学科体系及研究前沿和热点问题［J］. 水科学进展，2010，21 ( 4) : 479-489.( WANG Hao，YAN Denghua，JIA Yangwen，et al. Subject system of modern hydrology and water resources and research frontiers and hot issues ［J］. Advances in Water Science，2010，21( 4) : 479-489. ( in Chinese) )

［4］王浩，秦大庸，王建华，等. 区域缺水状态的识别及其多维调控［J］. 资源科学，2003，25( 6) : 2-7. ( WANG Hao，QIN Dayong，WANG Jianhua，et al. State identification and multiple regulation of regional water resources shortage［J］. Ｒesources Science，2003，25( 6) : 2-7. ( in Chinese) )

［5］CHEN Howen，CHANG Nibin.Using fuzzy operators to address the complexity in decision making of water resources redistribution in two neighboring river basins［J］.Advances in Water Resources，2010，33(6):652-666.

［6］SRDJEVIC B，MEDEIROSY D P，FARIA A S.An objective multi-criteria evaluation of water management scenarios［J］.Water Resources Management，2004，18:35-54.

［7］LOUKASA，MYLOPOULOSN，VASILIADESL.A modeling system of the evaluation of water resources management strategies in Thessaly，Greece［J］.Water Resources Management，2007，21:1673-1702.

［8］LAHLOH M，LARRY WC.Alternatives evaluation and selection in development and environmental［J］.Environ Impact Assess Rev，1993，13:37-61.

［9］吴泽宁，左其亭，丁大发，等.黄河流域水资源调控方案评价与优选模型［J］.水科学进展，2005，15(5):735-740.(WU Zening，ZUOQiting，DINGDafa，et al.Assessment and optimization model of water resources control alternatives for the Yellow River basin［J］.Advances in Water Science，2005，15(5):735-740.(in Chinese))

［10］OKEOLA O G，SULE B F.Evaluation of management alternatives for urban water supply using multicriteria decision analysis［J］.Journal of King Saud University-Engineering Sciences，2012，24:19-24.

［11］贾仰文，王浩，甘泓，等.海河流域二元水循环模型开发及其应用-Ⅱ:水资源管理战略研究应用［J］.水科学进展，2010，21(1):9-15.(JIA Yangwen，WANG Hao，GAN Hong，et al.Development and application of dualistic water cycle model in Haihe River Basin-Ⅱ:Strategic research and application for water resources management［J］.Advances in Water Science，2010，21(1):9-15.(in Chinese))

［12］丁勇，梁昌勇，方必合.基于D-S证据理论的多水库联合调度方案评价［J］.水科学进展，2007，18(4):591-597.(DING Yong，LIANG Changyong，FANG Bihe.Application of multi-reservoir flood control systems based on evidence theory［J］.Advances in Water Science，2007，18(4):591-597.(in Chinese))

［13］GAN Hong，ZHU Qilin，YOU Jinjun，et al.Alternative avaluation and selection based on order degree entropy:a case study of the Haihe River basin in China［J］.Journal of Food，Agriculture ＆ Environment，2010，8(2):1062-1066.

［14］朱启林.流域水循环多维调控方案评价研究［D］.北京:中国水利水电科学研究院，2010.

［15］肖燕，刘凌.流域复合系统协调度的评价方法研究［J］.水电能源科学，2009，27(3):15-17.(XIAO Yan，LIU Ling.Study on evaluation method of basin complex system coordinating degree［J］.Water Resources and Power，2009，27(3):15-17.(in Chinese))

［16］刘丙军，陈晓宏.基于协同学原理的流域水资源合理配置模型与方法［J］.水利学报，2009，40(1):60-66.(LIU Bingjun，CHEN Xiaohong.Water resources deployment model for river basin based on synergetic theory ［J］.Journal of Hydraulic Engineering，2009，40(1):60-66.(in Chinese))

［17］甘治国，蒋云钟，沈媛媛.以ET(蒸发蒸腾)为核心的水资源配置模型［C］//中国水利学会青年科技工作委员会.中国水利学会第三届青年科技论坛论文集.郑州:黄河水利出版社，2007:118-125.

［18］GAN Zhiguo，GAN Hong，WANG Lin，et al.Tradeoff approach of multiple objective analysis in the Haihe River Basin［J］.Journal of Food，Agriculture ＆ Environment，2010，8(3/4):991-995.