Large Deformation Dynamic Three-Dimensional Coupled Finite Element Analysis of Soft Biological Tissues Treated as Biphasic Porous Media

R.A.Regueiro,B.Zhang,S.L.Wozniak

1 Introduction

It is well-known that soft biological tissues are multiphase(oftentimes treated as a biphasic mixture of solid and fluid phases(Holmes,1986;Suh,Spilker,and Holmes,1991;Almeida and Spilker,1998;Levenston,Frank,and Grodzinsky,1998))and can undergo large deformations.Few researchers have considered inertia terms in the biphasic theory in studying wave propagation through soft biological tissues(Zhu and Suh,2000,2001).The flow of pore fluid relative to solid skeleton deformation(such as squeezing a saturated sponge)must be handled properly within a finite strain context,as well as considering inertia terms for dynamic loading when necessary,and implemented properly within a mixed Lagrangian finite element(FE)formulation,or other large deformation numerical method.For typical physiological dynamic loading such as encountered during normal athletic activities(e.g.,running,jumping),the relative acceleration of the fluid phasewith respect to solid phasemay be approximated as zero:At higher strain rates,however,such as encountered during shock loading and head impact(e.g.,leading to traumatic brain injury(TBI)),the relative acceleration of the fluid phase with respect to solid phase may not be zero(6= 000),requiring reformulation of the balance equations originally formulated for lower rate loading(such as normal athletic activities).Such extension is discussed in the paper,but all FE results currently assume≈.The mixed FE formulation and three-dimensional(3D)Q27P8 hexahedral FE implementation(27 solid skeleton displacement nodes,8 pore fluid pressure nodes,Fig.4)leads to a stable finite element method even for undrained loading conditions,such as those encountered at the initial transient of dynamic loading.A stabilized mixed formulation(Brezzi and Pitkaranta,1984;Truty and Zimmermann,2006;White and Borja,2008;Sun,Ostien,and Salinger,2013)Q8P8 hexahedral element is also implemented within the coupled dynamics framework,and results are compared with the Q27P8 element.The formulation for biphasic mixture theory at finite strain naturally calculates the build up of pore fluid pressure,and thus properly calculates,through the effective stress principle,the change in solid skeleton stress(i.e.,the“effective”stress)over time,when a biphasic soft tissue is subjected to dynamic loading.Also,after the initial transient,the variation of solid skeleton stresses will be naturally calculated as the fluid phase pressure dissipates over time.This is important for developing physiologically relevant degradation/damage hyperelastic,anisotropic constitutive models for soft biological tissues(Pena,2011;Balzani,Brinkhues,and Holzapfel,2012)within the context of biphasic mixture theory.The 3D FE implementation is conducted in Tahoe(tahoe.sourceforge.net),an opensource C++FE code,with more details provided in Ebrahimi(2007);Regueiro and Ebrahimi(2010),and formulation details in Li,Borja,and Regueiro(2004).

An outline of the remainder of the paper is as follows:Section 2 presents a brief overview of the theory of biphasic solid- fluid mixtures at finite strain,including kinematics,balance equations(linear momentum,and mass),and thermodynamics for constitutive equation forms.Section 3 also presents the stabilization term on the balance of mass for stabilized Q8P8 implementation.Section 4 presents numerical examples to test the performance of the Q27P8 versus Q8P8 elements,and also to study the importance of including inertia terms for simulating dynamic loading of soft biological tissues treated as porous media.Section 5 summarizes the results,conclusions,and future work.

Index notation will be used wherever needed to clarify the presentation.Cartesian coordinates are assumed,so all indices are subscripts,and the partial spatial derivative is the same as covariant spatial derivative(Eringen,1962).Some symbolic/direct notation is also given,such that(IJ=FiIFiJ,whereis the deformation gradient.Boldface denotes a tensor or vector.Subscript(•),iimplies a partial spatial derivative.Lowercase subscriptidenotes a leg of the tensor in the current configuration B,and capital subscriptI(s)denotes a leg of the tensor in the reference configurationof the solid skeleton.Superposed dot()Ds(2)/Dtdenotes material time derivative with respect to the solid skeleton motion.The symbolimplies a definition.

2 Biphasic(solid- fluid)mixture theory at finite strain:overview of theory and 3D FE implementation

The background for the theory of porous media at finite strain may be found primarily in Bowen(1980,1982);Coussy(2004);de Boer(2005),and originally in Truesdell and Toupin(1960).For other details on nonlinear solid mechanics,refer to Holzapfel(2000)and references therein.We follow the notation of Holzapfel(2000);de Boer(2005),and to some extent also Bowen(1980,1982).

2.1 Concept of volume fraction and mixture theory

The concept of volume fraction is illustrated in Fig.1 for the lung parenchyma(alveolar tissue for solid skeleton).The volume fractionsnαfor a biphasic mixture(solid(s)and fluid(f))relate “real”quantities with respect to the differential volumedvαof constituent α in the current configuration,versus the smeared quantity over the total differential volumedv,wherenα=dvα/dv,ordvα=nαdv.For example,the partial mass density of the α constituent is calculated as ρα= ραRnα(see Fig.1),where ραRis the real mass density of constituent α.Similarly,mass of constituent α,mα,over the total body B can be defined(see Fig.1).

2.2 Motion and kinematics,material time derivative

The kinematics of a biphasic solid- fluid mixture theory are shown in Fig.2.The vectoris the spatial position vector,which is simultaneously occupied by all

Likewise,the volumetric deformation of a solid- fluid mixture,that is smeared in the current configuration at spatial position vector,is shown in Fig.3.The differential

Figure 2:Kinematics of a biphasic(solid- fluid)mixture theory,showing solid skeleton composed of alveolar tissue.The continuum assumption of mixture theory is evident in the assumption that solid(s)and fluid(f)constituents coexist at the current position,although their velocitiesandmay be different;i.e.,6=,in general.

volumesdVfanddVsin their respective reference configurationsandboth map to the same differentialdvin the current configuration B,through their deformation gradients

The Jacobian of deformation for the two constituents is written as,

where we will typically drop the s superscripts and subscripts because the theory of porous media assumes we follow the motion of the solid skeleton.

Figure 3:Volumetric deformation of solid and fluid constituents in a biphasic mixture(solid skeleton composed of alveolar tissue of the lung parenchyma).

We convert all material time derivatives with respect to the solid phase motionsuch that for phase α,the material time derivative is,

whereis the relative velocity vector of the α phase with respect to the solid(s)phase motion.The material time derivative will be used in deriving the balance equations in the following sections.

2.3 Balance of mass(spatial and material descriptions)

For the balance of mass of the mixture,we write separately the balance of mass of each constituent,solid and fluid,expressing all material time derivatives in terms of the solid skeleton motion,and then add the two equations together to obtain the balance of mass of the mixture.The total mass of constituent α in B is written as(cf.Fig.1)

Taking the material time derivative of this spatial fieldmαwith respect to the motion of constituent α ,we can express the balance of mass of constituent α as

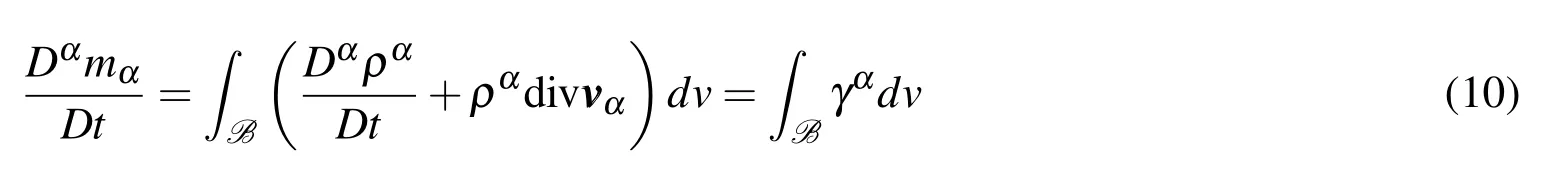
where γαis the mass supply rate for constituent α.If we assume compressibility of constituent α,assuming temperature is constant,we may write(Li,Borja,and Regueiro,2004)

wherepαis the mean Cauchy stress of constituent α,andKαis the bulk modulus.Then balance of mass for constituent α becomes:

We assume that the solid constituent is nearly incompressible,such thatns/Ks→0,and also that there is no supply of solid mass,such that γs=0.Using these assumptions,we can solve for the volume fraction of the solid phase asns=/Jsin closed form from the balance of mass equation for the solid phase by itself(Li,Borja,and Regueiro,2004).The volume fraction of fluid is then solved asnf=1−ns.The simplified form of the balance of mass of the biphasic(solid- fluid)mixture(to solve for Cauchy pore fluid pressurepf)then results as,when adding Eq.(12)for α=f,s,

We can map Eq.(13)back to the reference configuration of the solid phaseto obtain the following,

For a Total Lagrangian FE implementation,this is the equation from which we derive our variational equation for the weak form.

2.4 Balance of linear momentum(material and spatial descriptions)

Here,the balance of linear momentum of the biphasic solid- fluid mixture is presented.Carrying out the material time derivative of the linear momentum with respect to the α phase motion,applying the balance of mass of constituent α ,and using the divergence theorem on the traction term,we can localize the integral to obtain the balance of linear momentum for phase α in the current configuration as,

It is now relevant to discuss a principle that allows us to distinguish stress acting on the solid skeleton,and the pressure acting on the pore fluid(assuming the fluid is nearly inviscid,such as water).We apply the effective stress principle,which can be credited to Terzaghi(1943)(pg12)for saturated condition of soils,that states1The application of the effective stress principle to soft biological tissues has not been completely tested to date,but it is applied here for theoretical and numerical convenience.This is a topic of further research.

assume a nearly inviscid(no shear stress)isotropic fluid(e.g.,water),where then

Thus,we note that the partial solid stressis not equal to the effective stress=,unless the pore fluid pressurepf=0.The effective stress principle is useful for introducing constitutive equations for the solid skeleton separate from the pore fluid.

Starting with Eq.(15),we can map the balance of linear momentum of phase α back to the reference configuration of the solid phase.The partial first Piola-Kirchhoff stress α with respect to solid phase reference configuration is written as,

where subscript s denotes the reference configurationto which thejleg ofis mapped.It is then possible to arrive at the balance of linear momentum in the reference configuration of the solid phase(s)for phase α as,

Starting with Eq.(20),we can write each balance of linear momentum equation for solid(s)and fluid(f)phases,and use the following information to derive the balance of linear momentum of the solid- fluid mixture(s)+(f)in the reference configuration of the solid phase:

1.total Cauchy stress,and first Piola-Kirchhoff stress with respect to:

2.effective stress equation for Cauchy stress:

3.assume solid and fluid phase accelerations are nearly the same(for now):which may be appropriate for longer period motions like earthquakes and athletic activities, but likely not appropriate for high impact events experienced during car crash,or blast loading

4.assume all mass supplies are negligible:γα=0

5.assume body forces per unit mass are only due to gravity:is the acceleration vector of gravity

The resulting balance of linear momentum of the solid- fluid mixture(s)+(f)in the reference configuration of the solid phaseis then written as,

Eventually,for the Total Lagrangian finite element formulation,we will drop the s designation because the reference configuration will always be that of the solid skeleton(phase),such that,

where the superficial fluid velocity vector(nf)(a.k.a.,the Darcy velocity)is defined constitutively in Eq.(41).Then,upon substituting Eq.(29)into Eq.(28),we can write the balance of linear momentum for the fluid phase as,

Then,Eq.(30),upon mapping back to the solid skeleton reference configuration,including Eqs.(14),(23),we have three coupled balance equations to solve for three unknown fields:solid skeleton displacement, fluid phase displacement,and Cauchy pore fluid pressurepf.A similar procedure was followed for small strain by Jeremic,Cheng,Taiebat,and Dafalias(2008).This is left for future work.

2.5 Thermodynamics( first and second laws,constitutive equation forms)

Before we introduce constitutive equations,we briefly present the thermodynamics for a biphasic mixture.Using the first and second laws of thermodynamics,and assuming the existence of a Helmholtz free energy per unit mass of the α phase ψα,we derive the Clausius-Duhem inequality,which will be useful for defining constitutive model forms.

Applying the material time derivative to the total internal energy of phase α,using the balance of mass for α,divergence theorem on the traction term,and balance of linear momentum on α,and localizing the integral,we can derive the balance of energy of phase α in the current configuration B as,

whereeαis the internal energy per unit mass of α,is the heat flux vector,rαis the heat input rate per unit mass,andis the power density supply to phase α by other phases.The second law of thermodynamics for phase α is written in the current configuration B as,

where ηαis the entropy per unit mass,and θαis the temperature of phase α.To obtain the Clausius-Duhem inequality in the current configuration for phase α,we consider the existence of the Helmholtz free energy per unit mass for phase α in the current configuration ψαas,

Taking the material time derivative of Eq.(33),using the first law in Eq.(31),and substituting into the second law in Eq.(32),we arrive at the Clausius-Duhem inequality for phase α as,

We assume the solid constituent is nearly incompressible(is constant)and the fluid phase is compressible,such that the Helmholtz free energy per unit mass for the solid skeleton(s)inand fluid phase(f)in B are written as,

We write the Clausius-Duhem inequality for each phase(α=s,f)in Eq.(34),add them together,account for the functional forms of the Helmholtz free energy functions in their respective configurations in Eq.(35)(and B,respectively),and then derive the Clausius-Duhem inequality for the solid- fluid mixture as(all termspushed forward to the current configuration B,and localizing the integral),

The remaining terms in Eq.(37)comprise the reduced dissipation inequality as,

Furthermore,we assume thermodynamic conjugacy through proportionality parameters(permeability,and thermal conductivitieskθsandkθf),such that the following constitutive forms hold for generalized Darcy’s law,and Fourier’s law(assuming local thermal equilibrium such that mixture temperature θ =θs=θf):generalized Darcy’s law:

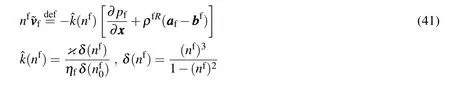
where κ is the intrinsic permeability, ηfis the fluid viscosity,and δ(nf)is the Cozeny-Karman relation for porosity dependence of(as a function of solid skeleton volume changeJsasnf=1−ns,ns=/Js),withthe initial porosity(Coussy,2004).

Fourier’s law:

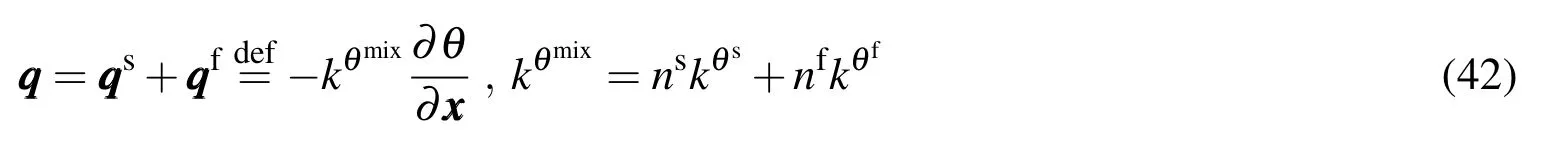
We now consider specific equations for the Helmholtz free energy functions:

Fluid:we assume the following form for the Helmholtz free energy function for the fluid:

wheregf(θf)is a temperature-dependent term,if needed.We assume homogeneous temperature,isothermal conditions for now.Using Eq.(38)2,we can derive the constitutive equation for the real mass density of the fluid ρfRin terms of the Cauchy pore fluid pressurepfas,

Solid skeleton:we assume the following form for the Helmholtz free energy function for the solid skeleton(neo-Hookean compressible isotropic elasticity(Ogden,1984)):

where(θs)is a temperature-dependent term.Using Eq.(38)1,we then derive the constitutive equation for the effective Second Piola-Kirchhoff stress as,

试验研究工作通过岩矿鉴定、化学多元素分析，确定了该矿矿石类型和相关元素含量。主要矿物成份由石膏、硬石膏及方解石、石英、长石、粘土质矿物及少量金属矿物等组成，根据化学分析结果和矿物学研究，该石膏矿有害组分含量低，符合加工水泥用缓凝剂用料标准。为了延缓硅酸盐水泥的缓凝时间，水泥生产企业便加入一定量的硬石膏于水泥熟料共同混合粉磨，以便水泥的凝结时间符合施工要求。石膏作为水泥的缓凝剂，用于调节水泥的凝结时间，同时也可增加水泥的强度，特别对矿渣硅酸盐水泥作用显著。矿石工业利用性能试验，是在内蒙古某公司水泥厂完成，该水泥生产线采用新型干法回转窑水泥生产工艺。

3 Stabilized Finite Element Implementation

The nonlinear finite element formulation and implementation(Newton-Raphson nonlinear solution, Newmark time integration) is discussed in Li, Borja, and Regueiro(2004);Ebrahimi(2007);Regueiro and Ebrahimi(2010),and thus details are not presented.We will focus on the stabilized term to be added to the variational equation for the balance of mass of the solid- fluid biphasic mixture as discussed in the references.

3.1 Stabilized term

For stabilizing the tri-linear hexahedral Q8P8 element near the undrained condition(upon transient loading,with low permeability,and assuming nearly incompressible fluid phaseKf→∞),we follow the approach of Truty and Zimmermann(2006),which is based on the method of Brezzi and Pitkaranta(1984).We attempted to apply the stabilization procedure of White and Borja(2008)for projecting pore fluid pressurepfby integral-averaging over an elemente,along with its weighting function value η,but based on our implementation,it was ineffective for our particular applications of soft tissues at finite strain.Sun,Ostien,and Salinger(2013)apparently were successful in extending the approach of White and Borja(2008)to finite strain,and they combined it with an assumed enhanced strain approach for the solid skeleton deformation gradient(for near incompressibility of the solid skeleton),which is an additional step we did not take in the paper.For our purposes,the Brezzi and Pitkaranta(1984)approach appears effective,and we will use it in the numerical examples.

After applying the method of weighted residuals to Eq.(14)(Hughes,1987),substituting Darcy’s law from Eq.(41),dropping the(•)sor(•)sdesignation,we obtain the variational equation of the mixture balance of mass in the reference configuration(of the solid skeleton)B0as,

where α is the stabilization parameter,andQfisnormal component of the pore fluid flux(positive inward)across the boundary.In Truty and Zimmermann(2006),an analysis was conducted to determine estimates of α for 3D problems,based on permeability, solid skeleton stiffness, pore fluid unit weight, time step, and finite element size,but since various assumptions were made on other factors,we ended up estimating α by a trial-and-error approach.Further investigation may be needed to more efficiently estimate α in the context of dynamic loading of biphasic soft tissues at finite strain.We note that although we have implemented theterm,it makes little difference in the results,and then may be left out of future simulations.

3.2 Element

For the mixed formulation,we use a Q27P8 hexahedral element as shown in Fig.4(Regueiro and Ebrahimi,2010).The stabilized Q8P8 hexahedral element just uses the vertex nodes 1-8.

4 Numerical examples

Three numerical examples are presented to demonstrate the Q27P8 and Q8P8 elements(no stabilization,and stabilized).The stable Q27P8 formulation is implemented in the FSSolidFluidMixT class in Tahoe,and the stabilized Q8P8 element is implemented in the FSSolidFluidMixQ8P8T class in Tahoe(stabilization is turned off by setting α=0).

4.1 Uniaxial strain compression using 3D FE

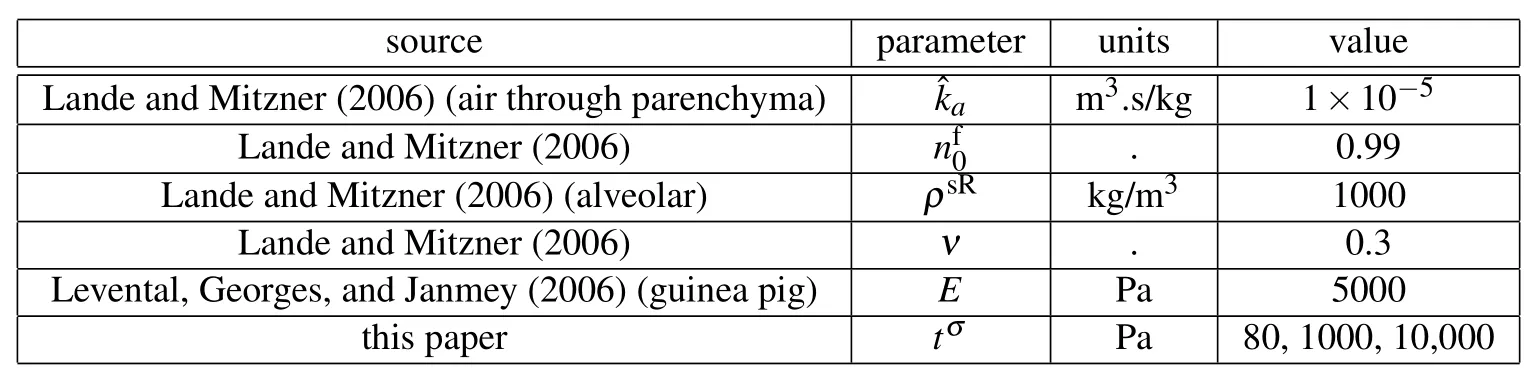
Table 1:Parameters for lung parenchyma examples.

To calculate the hydraulic conductivityfor water,we consider the intrinsic permeability calculated from the hydraulic conductivity for air(Lande and Mitzner,2006)κ=ηa=(1×10−5m2/Pa.s)(1.83×10−5Pa.s)=1.83×10−10m2.Then,we use the viscosity of water to calculate=κ/ηw=1.83×10−10m2/1×10−3Pa.s=1.83×10−7m2/Pa.s.The bulk moduli of air and water areKa=1×105Pa andKw=2.2×109Pa,respectively,at 20◦C.

Referring to Fig.5,we will consider three types of loadings and solutions:(1)drained(quasi-static,pore fluid pressurepf=0,tσ=1,000Pa),(2)consolidating(coupled pore fluid flow and solid skeleton deformation,tσ=1,000Pa),and(3)dynamic impulse loading(coupled pore fluid flow and solid skeleton deformation with inertia terms,tσ=10,000Pa).For each loading case,we keep the solid skeleton parameters the same for the lung tissue,and then assume the saturating fluid is either(a)air,or(b)water,with parameters given in Table 1.

Figure 5:Ten hexahedral element column mesh for the three analysis cases:(a)drained,(b)consolidating,(c)dynamic impulse.

For pore air,the solid skeleton vertical displacement upon traction loading is shown in Fig.6(a).It can be seen that given the low viscosity of the pore air,the drained and consolidating solutions are nearly the same,meaning the pore air pressure dissipates as the column is loaded over 0.1s,as illustrated in Fig.6(b).Nodes 8 and 91 are the locations where the solutions are plotted in Fig.5.In Fig.6(b),in addition to the pore fluid pressurepfbeing plotted with time,the mean effective Cauchy stressp0,and effective vertical stressare plotted.Recall thatandp0are positive in tension,andpfis positive in compression.Gravity is ignored,and the problem is uniaxial strain,soandare not zero,and thusp06=

Figure 6:(a)Vertical displacement,and(b)Stress for drained and consolidating solutions with pore air flow.

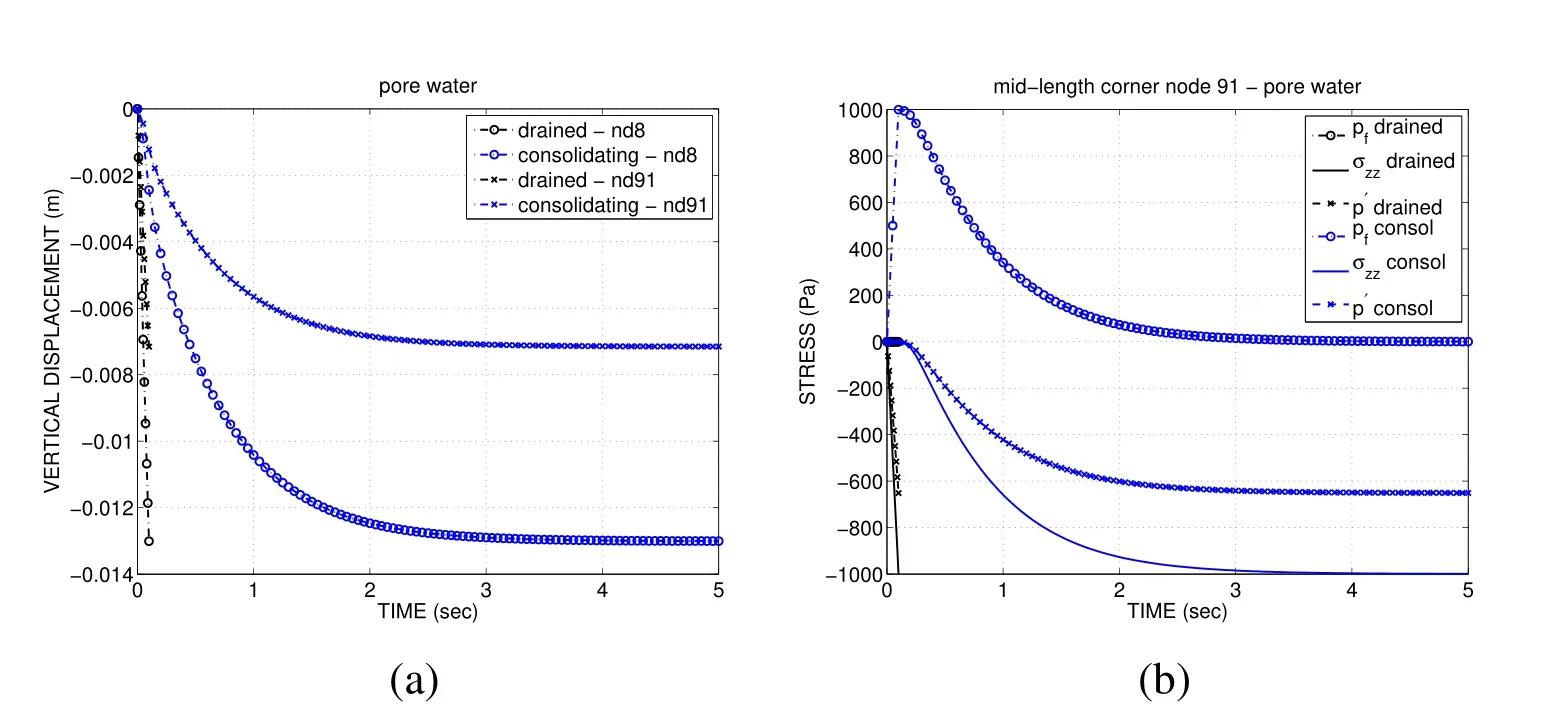
Figure 7:(a)Vertical displacement,and(b)Stress for drained and consolidating solutions with pore water flow.

Next,we conduct the same simulations,but switch out the pore fluid from air to water properties(viscosity,compressibility).The solid skeleton vertical displacement upon traction loading is shown in Fig.7(a).It can be seen that given the higher viscosity of the pore water,the drained and consolidating solutions are now different,as it takes longer for the pore water pressure to dissipate with time,as illustrated in Fig.7(b).

Now,to investigate the significance of inertia effects,a traction load oftσ=10,000 Pa is applied over 0.1s and then released over the next 0.1s for the pore air case(Fig.5),and loaded over 0.01s and unloaded over 0.01s for the pore water case.The effect of pore fluid(air and water) is investigated. We also study the effect of globally undrained BC as compared to the ends of the column being drained.In Fig.8(a),we plot the vertical displacement versus time for nodes 8 and 91 for drained and undrained BCs for the coupled dynamic simulations with pore air.Recall that the bulk modulus of air at ambient temperature is relatively low(Ka=1×105Pa),thus in Fig.8(a)there is compressive vertical displacement even for the undrained BC case(as opposed to when there is pore water,which is nearly incompressible,and thus the displacement will be zero for the undrained BC case in Fig.9(a)).Also,in Fig.8(a),note that for the case with drained BC,there is compressibility of pore air and also relative flow of pore air,reaching a displacement near 0.06m,which for an initial column length of 0.1m,is nominally=0.06/0.1=60%axial strain,which is clearly a large strain(see Fig.8(c)for actual deformed mesh andpfcontour).In Fig.8(b),we see that for the undrained BC case,the pore fluid pressurepfspikes up to nearly 10,000Pa as expected(the applied traction load),while because of the compressibility of air and relative fluid flow even during globally undrained BCs,there is a small buildup of effective stress.

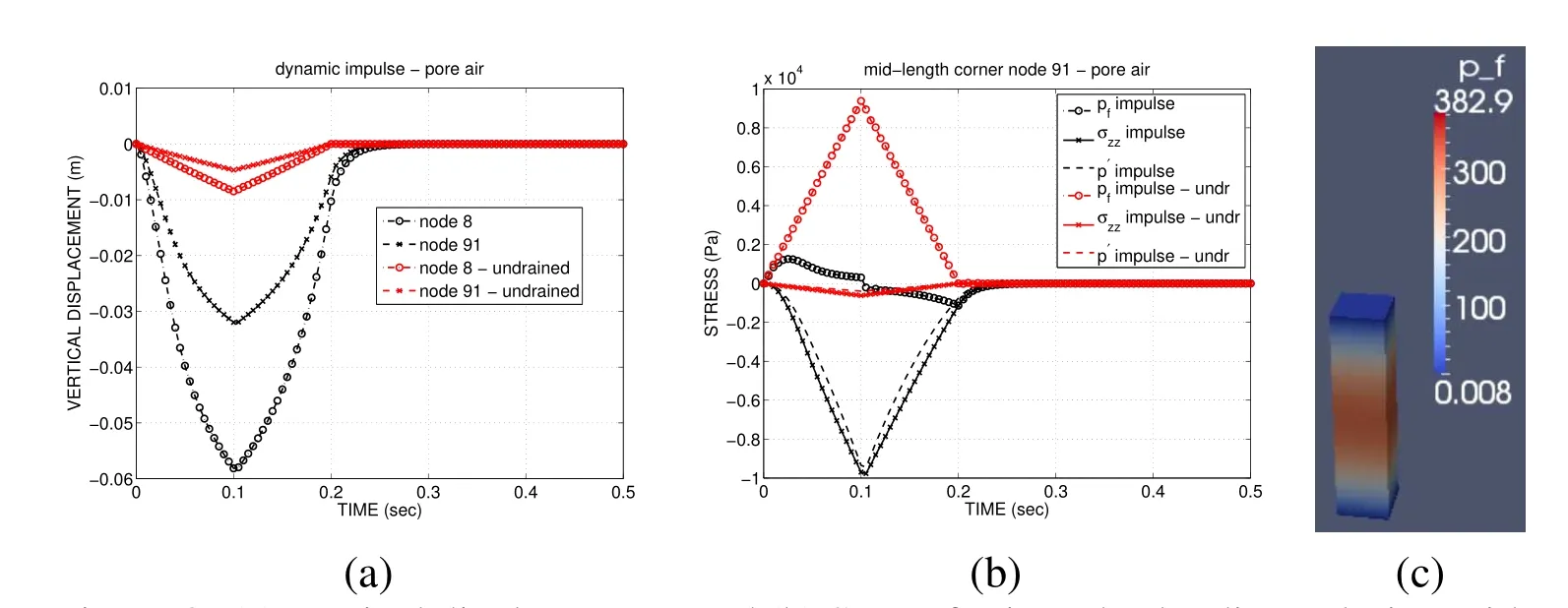
Figure 8:(a)Vertical displacement,and(b)Stress for impulse loading solution with pore air flow.(c)Actual deformed mesh for impulse loading with pore air flow,with drained BCs.Displacement magnification 1×.Note the large deformation.Note the original aspect ratio in Fig.5 for comparison.

Next,we run the simulation for pore water with 10,000Pa traction over 0.01s,with displacement results for drained and undrained BCs shown in Fig.9(a).We note now what we expect for undrained BC,that the displacement of the solid skeleton is zero because the pore water is nearly incompressible and the boundaries are impermeable.For the drained BC,we observe oscillation of the solid skeleton vertical displacement at nodes 8 and 91,which eventually damps out due to the relative fluid flow effect.Likewise,in Fig.9(b),we observe similar expected behavior,where for the undrained BC,the traction is completely taken up by the pore fluid pressurepf(tσ=10,000Pa),while the effective stress is zero.For the drained BC,pore fluid pressurepfbuilds up and oscillates,until it damps out to near zero at about 0.2sec.

Figure 9:(a)Vertical displacement,and(b)Stress for impulse loading solution with pore water flow.

Lastly,we compare the impulse solution as if the material were completely solid(no relative fluid flow;locally drained),with results shown in Fig.10.Since the real mass densities of solid and fluid(water)are the same for the lung alveolar tissue(ρsR= ρfR=1000kg/m3),the initial total mass density is also ρ0=1000kg/m3.We can compare the axial wave speed estimated from the curve in Fig.10(a)to the small strain theoretical solution as follows:

Figure 10(b)demonstrates the stress solution versus time,showing that for the solid dynamic solution(no pore fluid coupling),we get the expected oscillatory response,with little algorithmic damping for the Newmark time integration method used,with integration parameters β =0.3025,γ=0.6,unconditionally stable,with high frequency dissipation(pg534 of Hughes(1987)).Note that there is a clear difference between solid deformation analysis(locally drained material points,black curves)and coupled pore fluid flow with solid skeleton deformation analysis,for both undrained BC(red curves)and drained BC(blue curves).The drained BC(blue curve)would be closest to the actual experimental condition in the lab,whereas the undrained BC(red curves)could be replicated if the lung parenchyma tissue were completely sealed along its boundaries with an impermeable membrane.Clearly,the solid analysis (black curves) is not a reasonable assumption for the transient behavior of a soft biological tissue treated as a biphasic(solid- fluid)mixture at finite strain.

Figure 10:(a)Vertical displacement,and(b)Stress for impulse loading solution with pore water flow,compared to solid(locally drained)case.

4.2 Uniaxial strain compression,with stabilization

We now re-run the simulations for pore water consolidation and impulse loading,but decrease the permeability to=1×10−10m2/Pa.s to test the stabilization term in Eq.(47)for α =1× 10−6m3s2/kg.Results are presented in Fig.11 for pore fluid pressure contours,and Fig.12 for pore fluid pressure and vertical displacement versus time.We see in the contour plots the stable solution for Q27P8 element,with near uniform pore fluid pressure of 1000Pa in the middle of the mesh in Fig.11(a),and the unstable solution with the Q8P8 element,showing oscillatory pore fluid pressure along the depth of the mesh in Fig.11(b).In Fig.11(c),the solution is stabilized.The instability is evident in Fig.12 too,showing apparent consolidation,when the near undrained condition caused by low permeability should show slow decrease in pore fluid pressurepfand displacementdz,as is the case for the Q27P8 element and the stabilized Q8P8 element.

4.3 Pressure impulse loading of slab of lung parenchyma

The second numerical example considers a Neo-Hookean isotropic poroelastic slab loaded with a pressure pulse to observe transient response of effective stress and pore fluid pressure(Fig.13).The slab is initially assumed to be saturated with water.The top face of the slab is assumed drained,and the other faces are impermeable.

The dynamic loading of the slab as biphasic soft tissue is shown in Fig.13.The load-time schedule functions for drained,consolidating(same as load and hold for dynamic simulation),and dynamic load and release(impulse)are also illustrated in Fig.13.For constitutive parameters,we use the same as in Table 1.For the Q27P8 element,50 and 200 element meshes are considered.For the Q8P8 element,a 1350 element mesh is considered.

First,consider the drained and consolidating deformed meshes in Fig.14.This gives a general deformation pattern for the deformed meshes.Note nearly the same deformation is obtained with the 3 meshes.Next,consider the deformed meshes for dynamic simulation for hold and impulse loadings in Fig.15 for pore water,for the 50 Q27P8 element mesh.The hold loading generates more deformation and also higher peak pore fluid pressure than the impulse loading,as shown in Fig.16.

Figure 12:(a)Pore water pressure pfversus time at middle section of the mesh,comparing result of Q27P8 mesh(stable,blue lines)and Q8P8 meshes(nonstabilized(red)and stabilized(green)).(b)Displacement in z direction dzversus time at top and middle sections of the mesh,comparing result of Q27P8 mesh(stable)and Q8P8 meshes(non-stabilized and stabilized).

In Fig.16,we compare the pore fluid pressurepfat the corner node for the various analysis types.We see that for the dynamic hold loading,pfis much larger than for dynamic impulse loading.For all drained solutions,pf=0,and for the consolidating solution,there is a small negativepfbefore immediate consolidation(the solid skeleton at the bottom impermeable face is in tension).The 200 Q27P8 element mesh gives almost the exact same result as in Fig.16(a)(and is thus not shown),and the non-stabilized 1350 Q8P8 element mesh gives nearly the same result as in Fig.16(a),with result shown in Fig.16(b).Thus,for some soft biological tissues with higher permeability(such as the lung parenchyma,not the case for the low permeability vertebral disc),stable results can be achieved with the non-stabilized Q8P8 element implementation.In Fig.17,we compare displacementdyat the corner node for the various analyses,plotting over 0.1sec and 1sec.We see that the excited displacement frequencies are different for the dynamic hold and impulse simulations,the hold one having a higher frequency partly due to stiffening by enabling geometric nonlinearity.We see in Fig.17(c),the 1350 Q8P8 element mesh result is nearly the same as the 50 Q27P8 element mesh result in Fig.17(a).Given the small pore pressurepfgenerated during impulse loading(red curves in Fig.16),there is no noticeable difference between “dynamic impulse”and “dynamic impulse drained”displacement time histories in Fig.17,whereas for“dynamic hold”and “dynamic hold drained,”there is a small difference in displacement amplitude.

Figure 13:(top)Schematic of pressure loading of cantilevered poroelastic slab.(bottom)Various load schedule functions applied.

Figure 14:The deformed mesh for drained loading,and end of consolidation(no inertia terms)for pore water.Displacement units in meters,with displacement magnification 1×.(a)50 Q27P8 elements,(b)200 Q27P8 elements,(c)1350 Q8P8 elements.

Figure 15:The deformed meshes for dynamic simulation with pore water for hold(a)and impulse(b)loadings(with inertia terms).pfunits in Pa.

Figure 16:Plot of pore water pressure pfversus time for the various analyses.(a)50 Q27P8 element mesh results,(b)1350 Q8P8 element mesh results without stabilization.

Figure 17:Plot of displacement dyversus time for the various analyses((a)up to 0.1sec,(b)up to 1sec for 50 Q27P8 element mesh)for pore water.(c)1350 Q8P8 element mesh results without stabilization.

Next,we consider the deformed meshes for dynamic simulation for impulse and hold loadings in Fig.18 for pore air.In this case for pore air,the peak pore air pressures are not noticeably different between dynamic hold and impulse loadings,as also shown in Fig.19(a)forpfversus time.In Fig.19(b),we compare displacementdyat the corner node,plotting over 0.1sec for pore air.We see that the dynamic hold and impulse simulations have nearly the same frequency,while there is a small poromechanical effect noticeable for the dynamic impulse simulation(difference in curves after 0.05sec).For the Q8P8 element mesh,the results are similar as shown in Fig.20.

Figure 18:The deformed meshes for dynamic simulation with pore air for hold(a)and impulse(b)loadings(with inertia terms).pfunits in Pa.

Figure 19:50 Q27P8 element mesh results:(a)Plot of pore air pressure pfversus time for the various analyses.(b)Plot of displacementdyversus time for the various analyses.

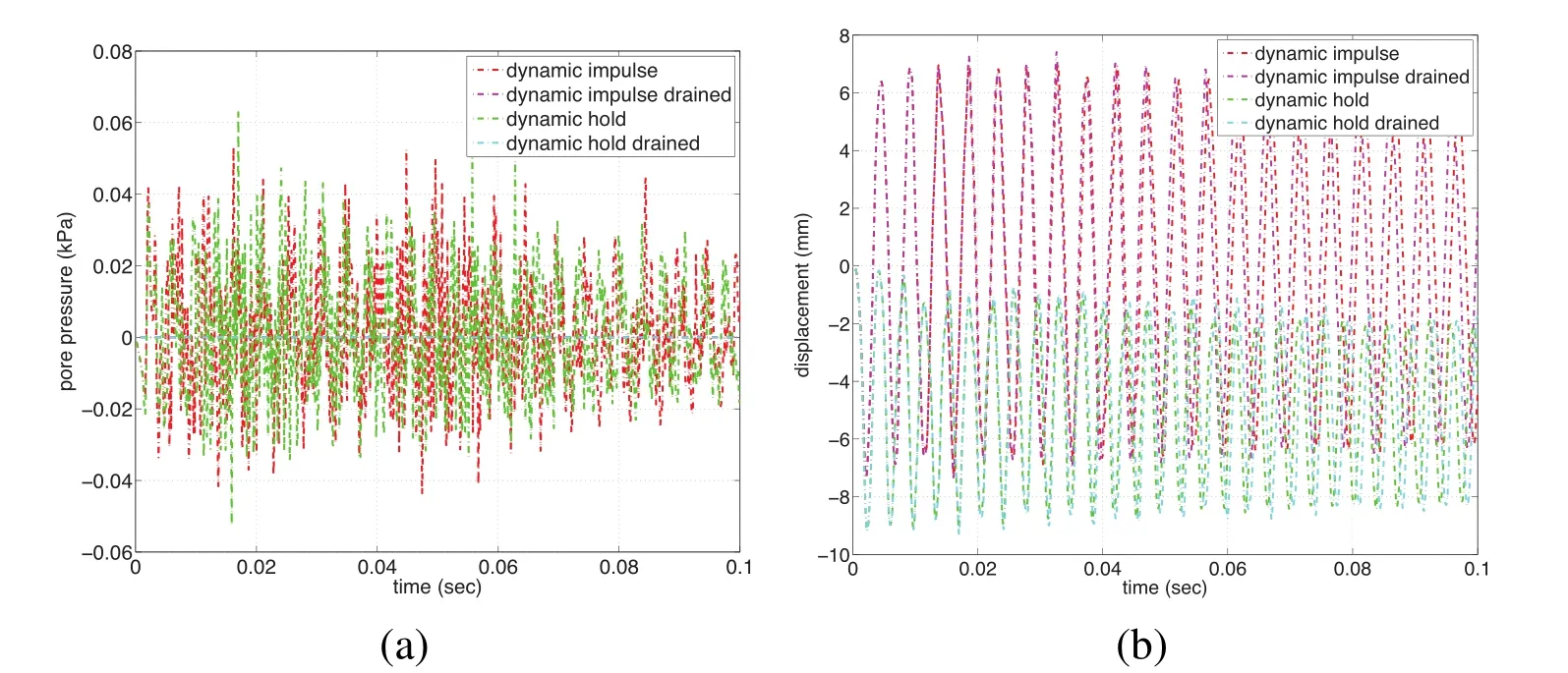
Figure 20:Non-stabilized 1350 Q8P8 element mesh results:(a)Plot of pore air pressure pfversus time for the various analyses.(b)Plot of displacement dyversus time for the various analyses.

In summary,for longer duration loadings(in this case,up to 0.1 sec),the pore water pressure can build up and thus affect the solid skeleton deformation,and in turn the effective stresses.When the pore water is substituted with pore air,differences in results are observed between the two pore fluids.For pore water(higher mixture mass density),different loadings(dynamic impulse,dynamic hold)trigger different modes of vibration at different frequencies.On the other hand,for pore air(lower mixture mass density),different loadings(dynamic impulse,dynamic hold)trigger the same mode of vibration(with slightly different frequencies due to geometric nonlinearities).For pore air,the overall mixture is less dense,thus the frequency of free or forced vibration is higher than when saturated with pore water;the permeability is 55×higher than for pore water,thus there is little build up of pore air pressure during dynamic loading of the thin slab.

Also,it was noted that there is no distinguishable difference between a 50 element and 200 element mesh for Q27P8 implementation,and likewise for a 1350 element Q8P8 mesh without stabilization.Because of the higher permeability of the lung parenchyma,the stabilizing term Hstabis not needed.We will see in the next example for the vertebral disc that has a much smaller permeability,the stabilizing term is needed to obtain meaningful,stable results.

4.4 Vertebral disc compression loading

Vertebral disc compression using the Q27P8 element,and Q8P8 element with and without stabilization,is simulated with parameters in Table 2(taken from Tables 1 and 2 of Williams,Natarajan,and Andersson(2007))and coarsest mesh in Fig.21;two finer Q8P8 meshes are shown in Fig.22.The geometry of the lumbar spine disc was simplified for the simulations.The annulus fibrosus was modeled as an ellipse with a major axis of 0.02646 m and a minor axis of 0.02016m with a height of 0.00945 m(minus the nucleus volume).The nucleus pulposus was modeled as an ellipse with a major axis of 0.02016 m and a minor axis of 0.01386 m with a height of 0.00945 m.The permeabilitiesˆkare averaged from the values reported in different directions in Williams,Natarajan,and Andersson(2007),assuming anisotropy in that paper;we assume isotropic permeability in this paper,which can be generalized for anisotropy in the future.A downward traction load of 0.5 MPa(Ferguson,Ito,and Nolte,2004)is applied,with similar time histories as shown in Fig.5 for drained,consolidating,and dynamic impulse.We do not verify that the material properties in Williams,Natarajan,and Andersson(2007)for annulus and nucleus of the disc,nor the compressive loading of 0.5MPa by Ferguson,Ito,and Nolte(2004)are physiologically correct or not.The purpose of the paper is to investigate the difference in results in assuming a drained versus consolidating versus dynamic(with inertia terms)coupled poromechanical analysis.All analyses use stabilization parameter α =1×10−6m3s2/kg.

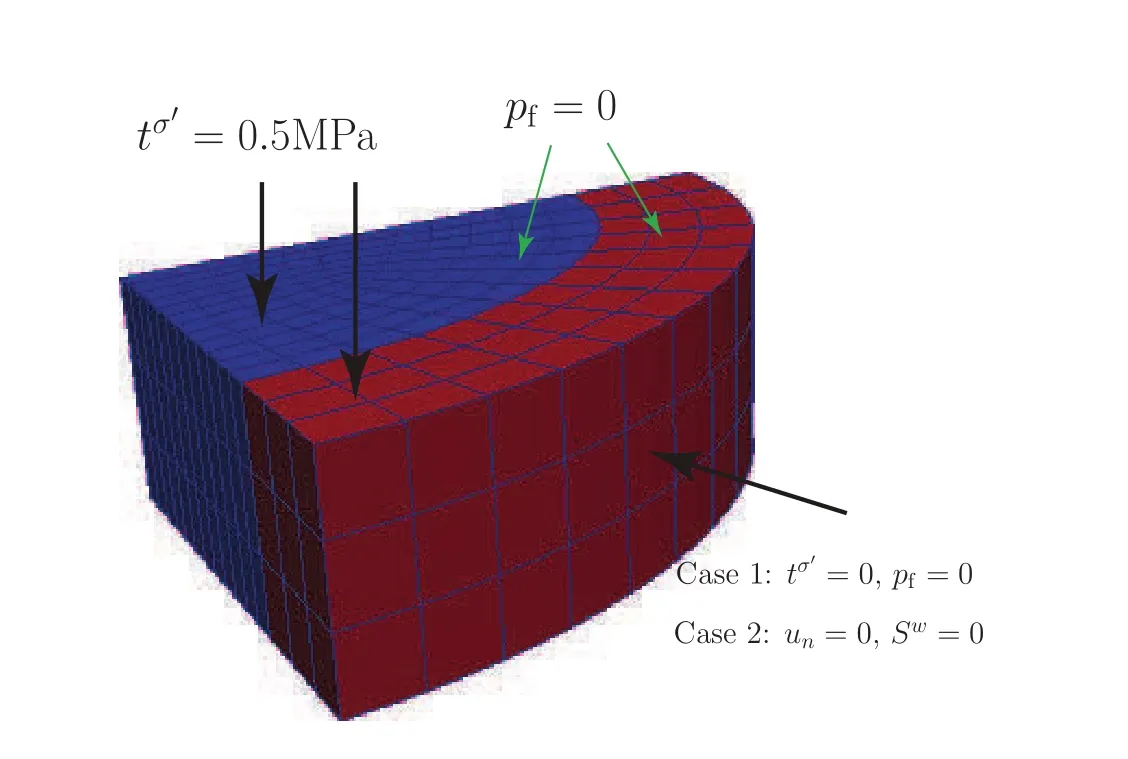
Figure 21:Coarsest mesh(432 elements)used in analyzing vertebral disc compression,showing applied effective traction tσ0and drained pf=0 boundary at top,and Cases 1 and 2 BCs on the curved surface of the annulus.The nucleus(blue)and annulus(red)sections are modeled as distinct materials.The symmetry planes are impermeable with fixed normal displacements.

4.4.1Vertebral disc compression loading with lateral expansion and drainage-Case 1

For the Case 1 BCs(tσ0=0,pf=0 on curved annulus surface)shown in Fig.21,we present the time histories of displacementdz(vertical,in direction of traction loading)anddx(lateral,along long axis),and pore fluid pressurepf,in Fig.25 for the three nodes shown in Fig.23.The time histories in Fig.25 provide a comparison between drained,consolidating,and dynamic impulse results,as well as various meshes(Q27P8 and Q8P8 element types).Unless otherwise indicated,it is assumed the result is that of the coarsest mesh(432 elements)with Q27P8 element type.In Fig.24,we see contour plots ofpfwith deformed meshes for the consolidating analysis.Note from Fig.25,that upon end of traction loading at 0.1s,the displacementsdzanddxand pore fluid pressurepfremain nearly constant,where in fact there is a slow consolidation process ongoing(note the small permeability values in Table 2 for nucleus and annulus).Another observation is that the Q27P8 mesh provides a higherpf,yet with nearly the same displacement as the stabilized Q8P8 meshes(see Fig.25).It is likely that in the stabilized Q8P8 mesh results,there is added diffusion of pore fluid leading to lowerpfvalues as observed in Fig.24.Mesh refinement on the Q27P8 mesh is required for further study,but given the expense of this element type,and the lack of parallel execution for the Q27P8 currently,we do not present finer mesh results for the Q27P8 element.The Q8P8 element can be executed in parallel computation.For the dynamic impulse analysis,given the three-dimensional nature of loading and pore fluid flow,the disc essentially damps out the impulse wave completely,with small oscillation after release of the impulse at 0.02s,as shown in Fig.25(a),(b)displacements.The drained results(no consolidation,and no inertia terms)are provided as a benchmark for deformation comparison.

Figure 22:Two finer Q8P8 meshes used in the disc compression analysis,showing nodes where analysis results are compared.Left mesh has 3,465 elements,and the right mesh has 16,875 elements.

Figure 23.Q27P8 deformed mesh for drained analysis of Case 1 BC(tσ′=0,pf=0).Observe the undeformed mesh for comparison.Displacement magnification 1×.

Figure 25:(a)Vertical displacement dz.(b)Lateral displacement dxalong long axis.(c)Pore fluid pressure pf.(d)Pore fluid pressure pfwithout Q27P8 result.

Figure 26:Q27P8 deformed mesh for drained analysis of Case 2 BC(un=0,Sw=0).Observe the undeformed mesh for comparison.Displacement magnification 1×.

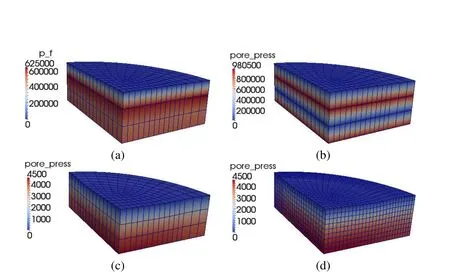
Figure 27:Deformed meshes(displacement magnification 1×),with contour of pore fluid pressure pf,for the following meshes:(a)coarse Q27P8 mesh(432 elements),(b)non-stabilized coarse Q8P8 mesh(432 elements),(c)stabilized coarse Q8P8 mesh(432 elements),(d)stabilized fine Q8P8 mesh(3465 elements).

Figure 28:(a)Vertical displacement dz.(b)Pore fluid pressure pf.(c)Pore fluid pressure pfwithout Q27P8 result.

4.4.2Vertebral disc compression loading in uniaxial strain-Case 2

For the Case 2 BCs(un=0,Sw=0 on curved annulus surface)shown in Fig.21,we present the time histories of displacementdzanddx,and pore fluid pressurepf,in Fig.28 for the same three nodes shown in Fig.23,with drained deformed mesh solution shown in Fig.26.Here,the higher pore fluid pressurepfgenerated in the Q27P8 element mesh indicates a near locking behavior because of the low permeability,that stiffens the overall compressibility of the disc such thatdzis less for the Q27P8 mesh versus the Q8P8 meshes with stabilization(see Fig.28(a)).The two stabilized Q8P8 meshes compare well with each other as seen in Fig.28(a),(c).Also note for non-stabilized Q8P8 coarse mesh,the classical oscillating pore fluid pressure is observed in Fig.27(b),which the stabilized term alleviates in Fig.27(c).Similar to Case 1,there is only a small oscillation in solid skeleton displacement upon release of the impulse traction,implying that the forced solid skeleton compression and driven pore fluid flow almost completely damps out the impulse load.

5 Conclusions

The paper presented finite strain three-dimensional finite element analysis(FEA)of coupled pore fluid flow and solid skeleton deformation of soft biological tissues at finite strain,including wave propagation(i.e.,inertia terms).Compressibility of the pore fluid is considered,as well as porosity dependent permeability.The FEA results of a full mixed formulation Q27P8(triquadratic in displacement,trilinear in pore fluid pressure)hexahedral element is compared to an equal order interpolation mixed formulation Q8P8(trilinear in displacement,trilinear in pore fluid pressure)hexahedral element with stabilization.It was shown that the stabilization method of Brezzi and Pitkaranta(1984)is effective for finite strain coupled FEA of biphasic mixtures of soft tissues with small permeability(such as the vertebral disc),and is not needed for higher permeability tissues(such as the lung parenchyma).It is useful to have the Q27P8 element implementation(even though computationally expensive),as a benchmark for comparison to the Q8P8 element implementation(non-stabilized,and stabilized).

Two soft biological tissues are considered:(1)lung parenchyma,and(2)vertebral disc.For(1),it was observed that switching out the pore fluid between water and air leads to different dynamical results,where the less viscous and lighter(but more compressible)pore air can nearly damp out any applied impulse wave,but also lead to different excited mode shapes as a result of the lower mass density.For the pore water case,some waves can be observed after application of an impulse traction load,but they are damped quickly due to the dissipation associated with relative pore fluid flow and solid skeleton deformation.For(2),given the low permeability of the disc,and assuming saturation by pore water,application of traction dynamic impulse load leading to large compressive solid skeleton deformation(and corresponding relative pore fluid flow)does not allow any significant waves to propagate in time,providing a near fully damped response,but with observable change in pore fluid pressure.

It is clear that there is an interplay of solid skeleton deformation(and,in turn,solid skeleton effective stress)and build-up of pore fluid pressure over time,that would not be properly accounted for by a more simple finite strain viscoelastic constitutive model,without treating the soft tissue as a biphasic mixture.The effective stress governs the constitutive response of the solid skeleton,which is influenced by the changing pore fluid pressure with time.Thus,if appropriate anisotropic,damage constitutive models are to be considered for soft biological tissues loaded dynamically(such as during impact or blast loading),the biphasic nature of the soft tissue should be taken into account.With that said,the paper provides a glimpse into how such biphasic dynamic (with inertia terms) analyses may be conducted,benchmarking against drained and consolidating FEA results,with further research needed:(i)consider physiological BCs and tissue geometries for in-vivo conditions;(ii)more study of the stabilization parameter α and how to select it for various tissue elastic moduli,geometries,etc.;(iii)anisotropic permeability and solid skeleton constitutive models appropriate for fibrous soft biological tissues;(iv)inclusion of pore fluid acceleration vector different than solid skeleton accelerationand modification of the coupled governing equation solution algorithm(see Remark 1 in Sect.2.4);and(v)extension to dynamic explicit analysis capability for high rate dynamic loading.

Acknowledgements

The work was funded by grant W81XWH-10-1-1036 from the United States Army Medical Research and Materiel Command(USAMRMC).RAR was also funded through the U.S.Army Research Office Scientific Services Program administered by Battelle Memorial Institute,under contract W911NF-011-D-0001.SLW was funded through contract W911QX-09-C-0057 from the U.S.Army Research Laboratory.RAR acknowledges support from a UPS Foundation visiting professorship in the Department of Civil and Environmental Engineering at Stanford University during the writing of the article.

Almeida,E.;Spilker,R.(1998): Finite element formulations for hyperelastic transversely isotropic biphasic soft tissues.Comput.Methods Appl.Mech.Engrg.,vol.151,pp.513–538.

Balzani,D.;Brinkhues,S.;Holzapfel,G.(2012):Constitutive framework for the modeling of damage in collagenous soft tissues with application to arterial walls.Computer Methods in Applied Mechanics and Engineering,vol.213-216,pp.139–151.

Bowen,R.(1980):Incompressible porous media models by use of the theory of mixture.Int.J.Engrg.Sci.,vol.18,pp.1129–1148.

Bowen,R.(1982): Compressible porous media models by use of the theory of mixtures.Int.J.Engrg.Sci.,vol.20,pp.697–735.

Brezzi,F.;Pitkaranta,J.(1984): On the stabilization of finite element approximations of the Stokes problem.In Hackbusch,W.(Ed):Efficient Solutions ofElliptic Problems,Notes on Numerical Fluid Mechanics,volume 10,pp.11–19.Vieweg,Wiesbaden.

Coleman,B.D.;Noll,W.(1963):The thermodynamics of elastic materials with heat conduction and viscosity.Arch.Ration.Mech.Anal.,vol.13,pp.167–178.

Coussy,O.(2004):Poromechanics.John Wiley&Sons.

de Boer,R.(2005):Trends in Continuum Mechanics of Porous Media:Theory and Applications of Transport in Porous Media.Springer.

Ebrahimi,D.(2007):Three-dimensional finite element implementation for a dynamic solid- fluid mixture at finite strain.MS Thesis,University of Colorado at Boulder,2007.

Eringen,A.(1962):Nonlinear Theory of Continuous Media.McGraw-Hill,1 edition.

Ferguson,S.;Ito,K.;Nolte,L.-P.(2004): Fluid flow and convective transport of solutes within the intervertebral disc.Journal of Biomechanics,vol.37,pp.213–221.

Holmes,M.(1986): Finite deformation of soft tissue:Analysis of a mixture model in uni-axial compression.Journal of Biomechanical Engineering,vol.108,no.4,pp.372–381.

Holzapfel,G.A.(2000):Nonlinear Solid Mechanics:A Continuum Approach for Engineering.John Wiley&Sons.

Holzapfel,G.A.;Gasser,T.C.(2000):A new constitutive framework for arterial wall mechanics and a comparative study of material models.J.Elast.,vol.61,pp.1–48.

Hughes,T.J.R.(1987):The Finite Element Method.Prentice-Hall:New Jersey.

Jeremic,B.;Cheng,Z.;Taiebat,M.;Dafalias,Y.(2008):Numerical simulation of fully saturated porous materials.Int.J.Numer.Anal.Methods Geomech.,vol.32,pp.1635–1660.

Lande,B.;Mitzner,W.(2006): Analysis of lung parenchyma as a parametric porous medium.J.Appl.Physiol.,vol.101,pp.926–933.

Levenston,M.;Frank,E.;Grodzinsky,A.(1998): Variationally derived 3-field finite element formulations for quasistatic poroelastic analysis of hydrated biological tissues.Comput.Methods Appl.Mech.Eng.,vol.156,no.1-4,pp.231–46.

Levental,I.;Georges,P.;Janmey,P.(2006):Soft biological materials and their impact on cell function.Soft Matter,vol.2,pp.1–9.

Li,C.;Borja,R.;Regueiro,R.(2004):Dynamics of porous media at finite strain.Comp.Meth.App.Mech.Engr.,vol.193,no.36-38,pp.3837–70.

Ogden,R.W.(1984):Nonlinear Elastic Deformations.Chicheste,Ellis Horwood.

Pena,E.(2011):Prediction of the softening and damage effects with permanent set in fibrous biological materials.Journal of the Mechanics and Physics of Solids,vol.59,no.9,pp.1808–1822.

Regueiro,R.;Ebrahimi,D.(2010): Implicit dynamic three-dimensional finite element analysis of an inelastic biphasic mixture at finite strain.Part 1:application to a simple geomaterial.Comp.Meth.App.Mech.Engr.,vol.199,pp.2024–2049.

Suh,J.-K.;Spilker,R.;Holmes,M.(1991): A penalty finite element analysis for non-linear mechanics of biphasic hydrated soft tissue under large deformation.Int.J.Numer.Methods Engrg.,vol.32,pp.1411–1439.

Sun,W.-C.;Ostien,J.;Salinger,A.(2013):A stabilized assumed deformation gradient finite element formulation for strongly coupled poromechanical simulations at finite strain.Int.J.Numer.Anal.Meth.Geomech.,DOI:10.1002/nag.2161,2013.

Terzaghi,K.(1943):Theoretical Soil Mechanics.John Wiley and Sons.

Truesdell,C.;Toupin,R.(1960):The classical field theories.Handbuch der Physik,Springer,Berlin.

Truty,A.;Zimmermann,T.(2006):Stabilized mixed finite element formulations for materially nonlinear partially saturated two-phase media.Comput.Methods Appl.Mech.Engrg.,vol.195,pp.1517–1546.

White,J.;Borja,R.(2008): Stabilized low-order finite elements for coupled solid-deformation/ fluid-diffusion and their application to fault zone transients.Comp.Meth.App.Mech.Engr.,vol.197,no.49-50,pp.4353–4366.

Williams,J.;Natarajan,R.;Andersson,G.(2007):Inclusion of regional poroelastic material properties better predicts biomechanical behavior of lumbar discs subjected to dynamic loading.Journal of Biomechanics,vol.40,pp.1981–1987.

Zhu,Q.;Suh,J.-K.F.(2000): Dynamic finite element analysis of biphasic poroviscoelastic model for hydrated soft tissue..Annals of Biomedical Engineering,vol.28,no.SUPPL.1,pp.S–50.

Zhu,Q.;Suh,J.-K.F.(2001):Dynamic biphasic poroviscoelastic model simulation of hydrated soft tissues and its potential applications for brain impact study.InAmerican Society of Mechanical Engineers,Bioengineering Division(Publication)BED,pp.835–836.Snowbird,UT,United states.