Optimal Analysis for Shakedown of Functionally Graded(FG)Bree Plate with Genetic Algorithm

H.Zheng,X.Peng,3,4and N.Hu

1 Introduction

The rapid development of aircraft and space technologies requires materials to work in more and more severe environments,such as high and varying temperature with large temperature gradients.With the distributions of the thermal and mechanical properties properly designed according to the requirements in practical applications,functionally graded materials(FGMs)play an irreplaceable role in improving the performance of the composite materials.The gradient distribution of the thermal and mechanical properties in composites,induced by the change in the distribution of the reinforcement phase,endues FGMs with excellent adaptability to severe loading and environment conditions[Lee(1994)].

The development achieved in recent years implies the great potential of FGMs in a wide range of thermal,biomedical and structural applications[Sureshet al.(1998);Watariet al.(2004);Reddy(2011);Qiuet al.(1999);Taniet al.(2001)],and the plate structures made of FGMs have also been widely used in practical engineering.Great progress has been made in the research in the mechanical properties of Functionally graded plates(FGPs),such as buckling,bending and vibration[Feldomanet al.(1997);Na and Kim(2006);Aghabaei and Reddy(2009);Altenbach and Eremeyev(2009);Wu and Huang(2009)],crack and thermal fracture[Wanget al(2000);Guoet al.(2005)],transient thermal stress[Chenget al.(2000);Velet al.(2002,2003);Andrewet al.(2010)],static and dynamic responses[Zhonget al.(2003);Elishakoffet al.(2005);Gilhooleyet al.(2007)],shakedown analysis[Penget al.(2009a,b)],etc.

On the other hand,the concept of FGMs also provides possibilities for optimizing the microstructure parameters of composites to achieve high performance and better utilization of materials[Noda(1990)].The design of the distributions of the thermal and mechanical properties in FGMs has always been an important topic of research since the concept of FGMs was proposed.It is largely due to the excellent and unique advantages of FGMs,for instance,the combination of the advantages of different materials,the compatibilities between different materials and the good adaptability to various environments[Parashkevova(2004)].In the past decade,considerable attention has been devoted to FGM representations(Computer-Aided Design),design validation(Computer-Aided Engineering),fabrication(Computer-Aided Manufacturing)and material heterogeneity optimization[Kou(2012)].

In the development of modern structures,optimization is one of the most essential topics in the development of FGMs.Markworth and Saunders(1995)optimized the ceramic/metal composition with certain constraints to maximize or minimize the heat fl ux through the materials,where the normal thermal stress pro files were calculated and some unusual behavior was found.Ootaoet al.(1999)optimized the composition in an inhomogeneous hollow sphere with arbitrarily distributed and continuously varying material properties with a neural network approach.Cho and Ha(2002)optimized the volume fraction of Al2O3particles in a Ni/Al2O3composite to minimize the steady state thermal stress,in which the interiorpenalty-function method and the golden section method were employed,together with finite differential method for the sensitivity analysis and an appropriate material property estimation for calculating the thermo-mechanical properties in the graded layer.Chen and Tong(2005)presented a systematic numerical technique to perform sensitivity analysis of coupled thermo-mechanical problems.General formulations were presented based on finite element model by making use of the direct and the adjoint methods.

The initial progress in the analysis of the shakedown of the FG Bree plate,which is subjected to the coupled constant mechanical loading and cyclically varying temperature loading,has been reported in the authors’previous papers[Penget al.(2009a,b);Zhenget al.(2012)].Different from our previous work,in this paper we focus on the optimal distribution of the reinforcement particles in the FG Bree plate,for the purpose to enhance the capability of the FG plate to bear cyclic thermal loading.In order to achieve a more accurate result,we characterize the distribution of the material properties in the thickness of a FG Bree plate with a piecewise exponential distribution[Guoet al.(2007)],and the effective mechanical property of a material element of the FG plate is evaluated with a double-inclusion mean field approach[Juet al.(1994)].Recent developments of"Computational Grains"also enable a direct simulation of a large number of inclusions for composite or FGM,without FEM meshing of inclusions/matrix[Dong,et al.(2012a,b;2013)].In order to achieve the best shakedown capability of the FG plate,the distribution of reinforcement particles is optimized with the Genetic Algorithm(GA)[Cavalcantiet al.(1997);Chenet al.(2000);Choet al,(2004);Huanget al.(2002);Khalilet al.(2004);Kouet al.(2006,2009);Praveenet al.(1998);Wadleyet al.(2003);Williamset al.(2005)].The optimization model for the shakedown of the FG plate is programmed in MATLAB.Two numerical examples are presented to demonstrate the validity of the proposed approach.

2 Constitutive model,static and kinematic shakedown theorems

Assuming small deformation,for initially isotropic and plastically incompressible materials,the constitutive model adopted can be expressed as

where εijis strain,are its elastic,plastic and thermal components,respectively,which are determined with

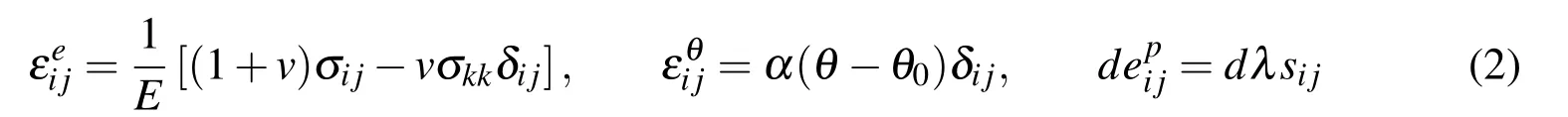
whereE,ν and α are the Young’s modulus,the Poisson’s ratio and the coefficient of linear expansion,respectively,σijandsijare stress and its deviatoric component,θ andθ0are temperature and reference temperature,respectively,δijis the Kronecker delta,and[Penget al.,(1996)]

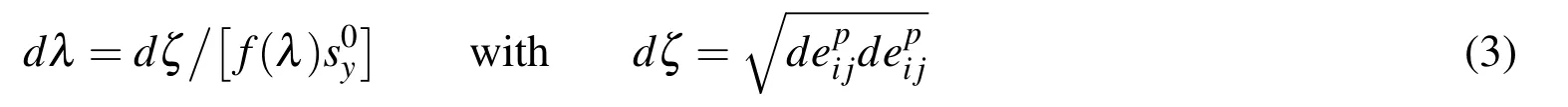
s0yis a material constant related to initial yield andf(λ)＞0 is a function describing the hardening of material.It can be seen thatdλ is non-negative in any plastic deformation process.The following hardening function is adopted in analysis,

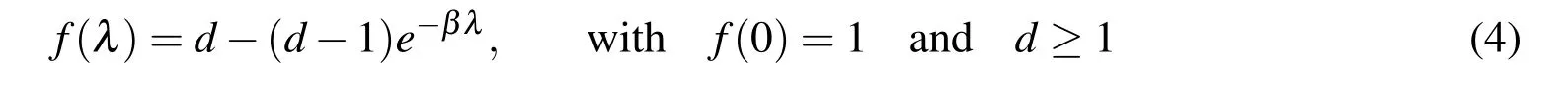
It can be seen in Eqs.(3)and(4)thatf(λ)increases with the development of plastic deformation and tends to an asymptotic valuedcorresponding to the ultimate strength σy=d·σ0yas plastic deformation fully develops when λ →∞,indicating a saturated state of hardening.Substituting Eq.(3)into Eq.(2)3yields the following Mises-type yield condition

Introducing the following loading function

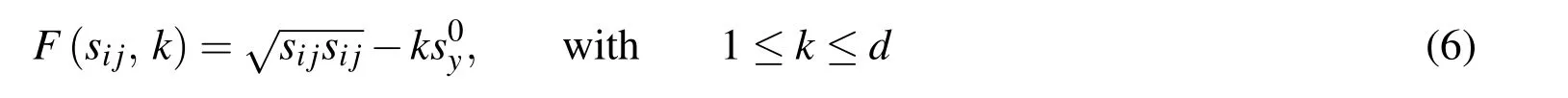
It can be seen that any state of stress should satisfyF(sij,k)≤0,andF(sij,k)=0 de fi nes a loading surface.

Given a set of actual stress and hardening states,sijandk,and a set of allowable stress and hardening states,s∗ij,k∗,which satisfy

And making use of the following inequality

One can prove that[Penget al.(1993)]

2.1 Static Shakedown Theorem[Peng et al.(2009a)]

If there exist a time-independent residual stress fieldρ¯ijand a time-independent fieldk∗such that for all the load variations within a given load domain Ω,the following condition holds

then the total energy dissipated in any allowable load path is bounded.

In Ineq.(10),sEijis the purely elastic solution of the deviatoric stress determined by external loads and 1≤k∗≤d.

2.2 Kinematic Shakedown Theorem[Peng et al.(2009a)]

If there exist over a certain time interval(t1,t2),a history of load resulting in a history of purely elastic stresssEij(x,t),and a history of plastic straine¯ij(x,t)resulting in a kinematic ally admissible increment such that

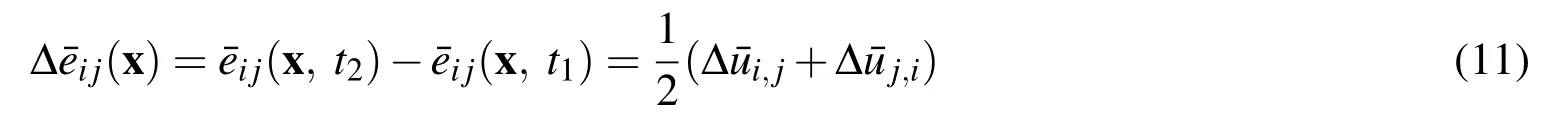
with∆¯ui=0 onSu(the boundary where displacement is prescribed),and if shakedown occurs in the given structure,the condition as Ineq.(12)should be satisfied for all kinematically admissible plastic strain cycles.

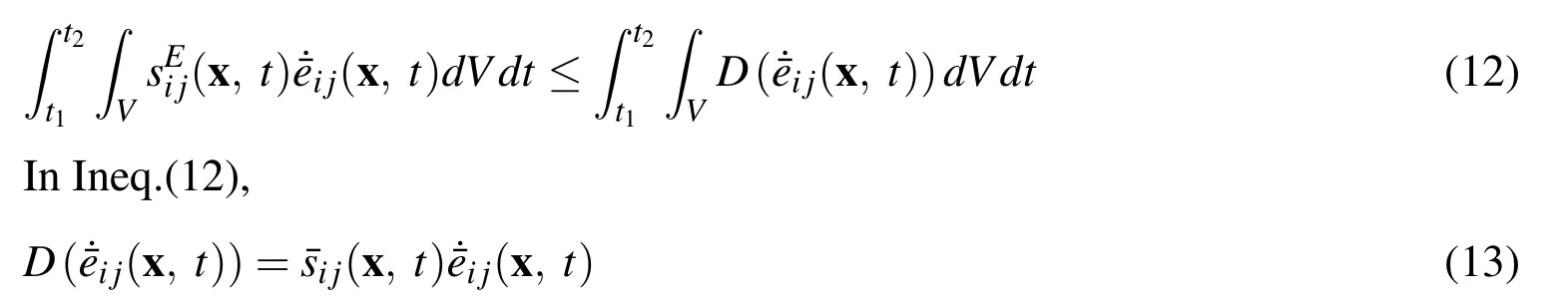
is a dissipation function.

The following relationship can be obtained for practical application by substituting Eq.(2)3and Eq.(3)into Ineq.(12)by following the definition by König(1987),

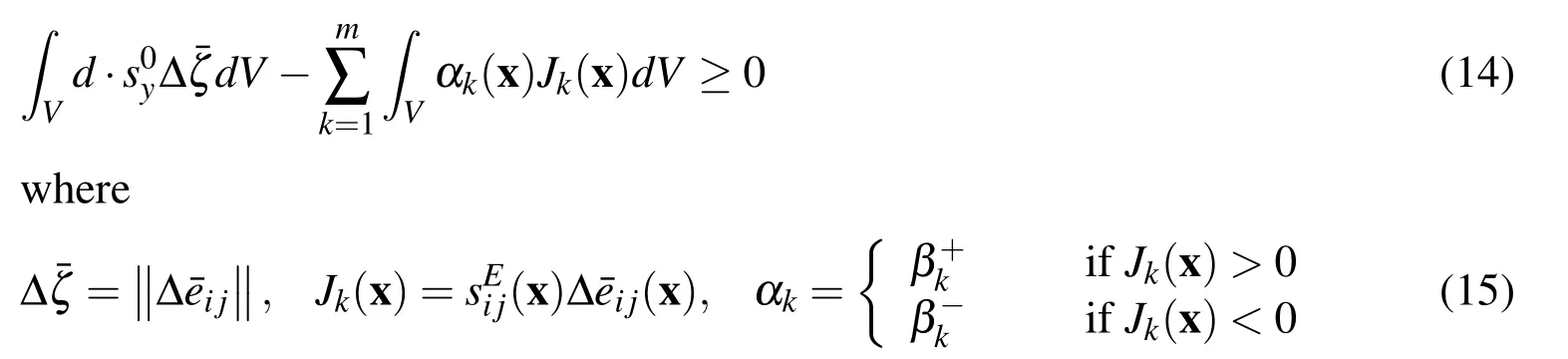
and a set of inequalities βk-≤βk≤βk+(k=1,2,...,m)de fi nes the domain Ω of loads.

3 Optimal model

3.1 The Bree plate

A plate(Figure 1)of thicknesshis subjected to loads(Px,Py)per unit length in two mutually orthogonal directions.The surfaces of the plate are subjected to temperatures θ2and θ1which vary cyclically,as shown in Figure 1.The cycle time ∆tis assumed large compared with characteristic heat conduction time,and the change,between θ0(a reference temperature)and θ0+∆¯θ,is assumed to take place sufficiently slowly for steady state conditions of prevail.The strain εxand εyare assumed to be uniform throughout the thickness of the plate.This problem is a simulation of the behavior of a thin walled tube,in the context of a nuclear fuel can design problem by Bree(1967)for homogeneous material and perfect plasticity.

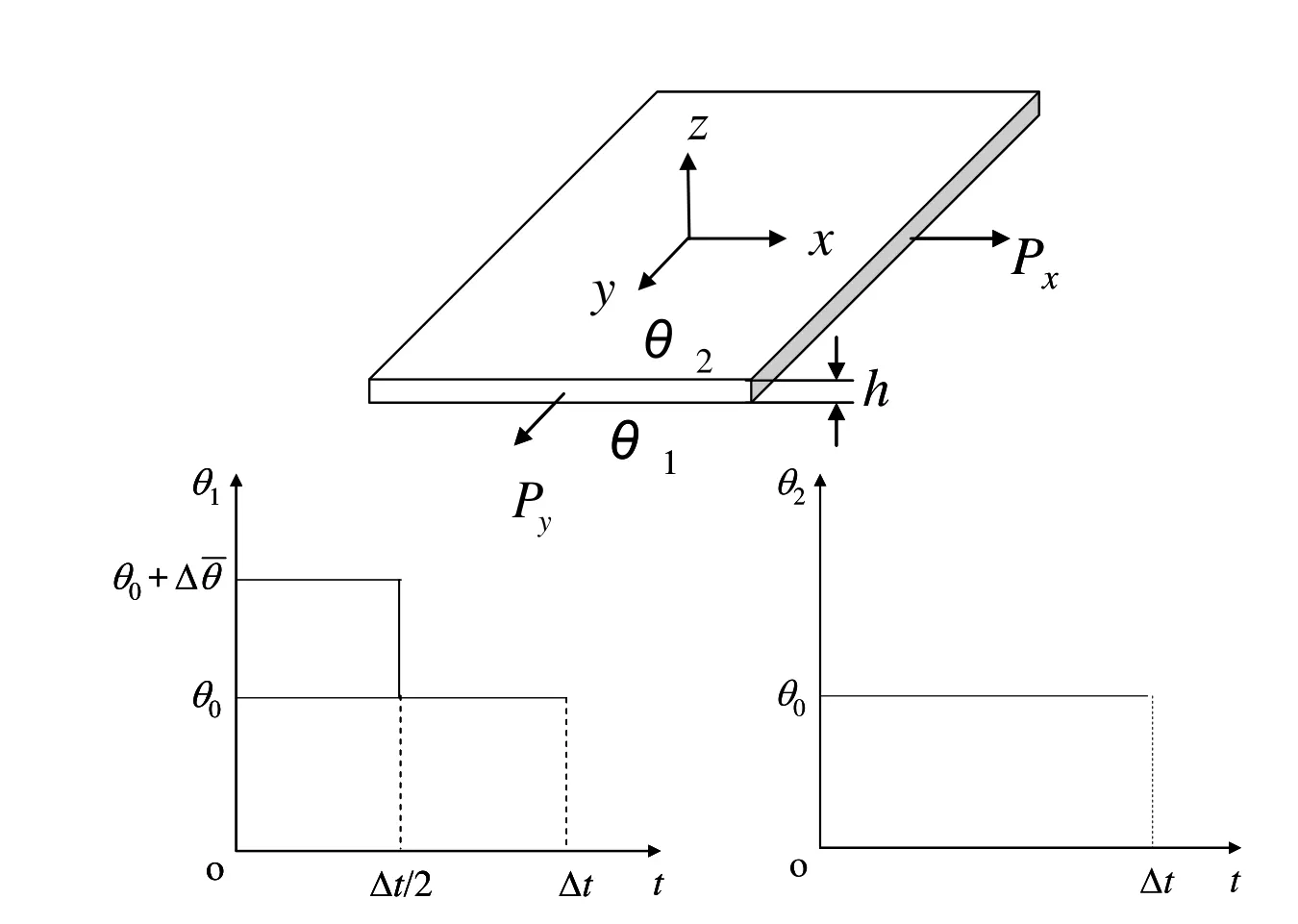
Figure 1:The Bree plate.

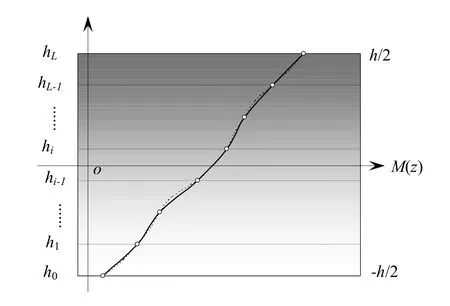
Figure 2:Piecewise-exponential distribution model for FG plate with arbitrarily distributed properties.

3.2 PWED model and material properties

The piece-wise exponential distribution model(PWED model)[Guoet al.(2007)]is adopted for the distribution of the material properties in an FG plate,as shown in Figure 2.The plate is assumed to be divided intoLparallel layers in the direction of thickness,in each of which the thermal-mechanical properties vary exponentially in the direction of thickness.By this way,the actual thermal-material properties of the plate can be approximated with a set of exponential functions.At both surfaces of a layer the properties are identical with the actual properties of the material.Therefore,the properties of an FG plate can be approximated with sufficient accuracy if the thickness of each layer is sufficiently small.

The plate of thicknesshis assumed to be divided intoLparallel layers,each of which is marked with subscripti(i=1,2,...,L)counting from the bottom surface of the plate,thei-th layer is located betweenz=hi-1andz=hiand at the bottom surfaceh0=-h/2,while at the top surfacehL=h/2.SupposefM(z)is the real distribution of a thermal/mechanical property in a layer,we can approximatefM(z)withM(z),i.e.,

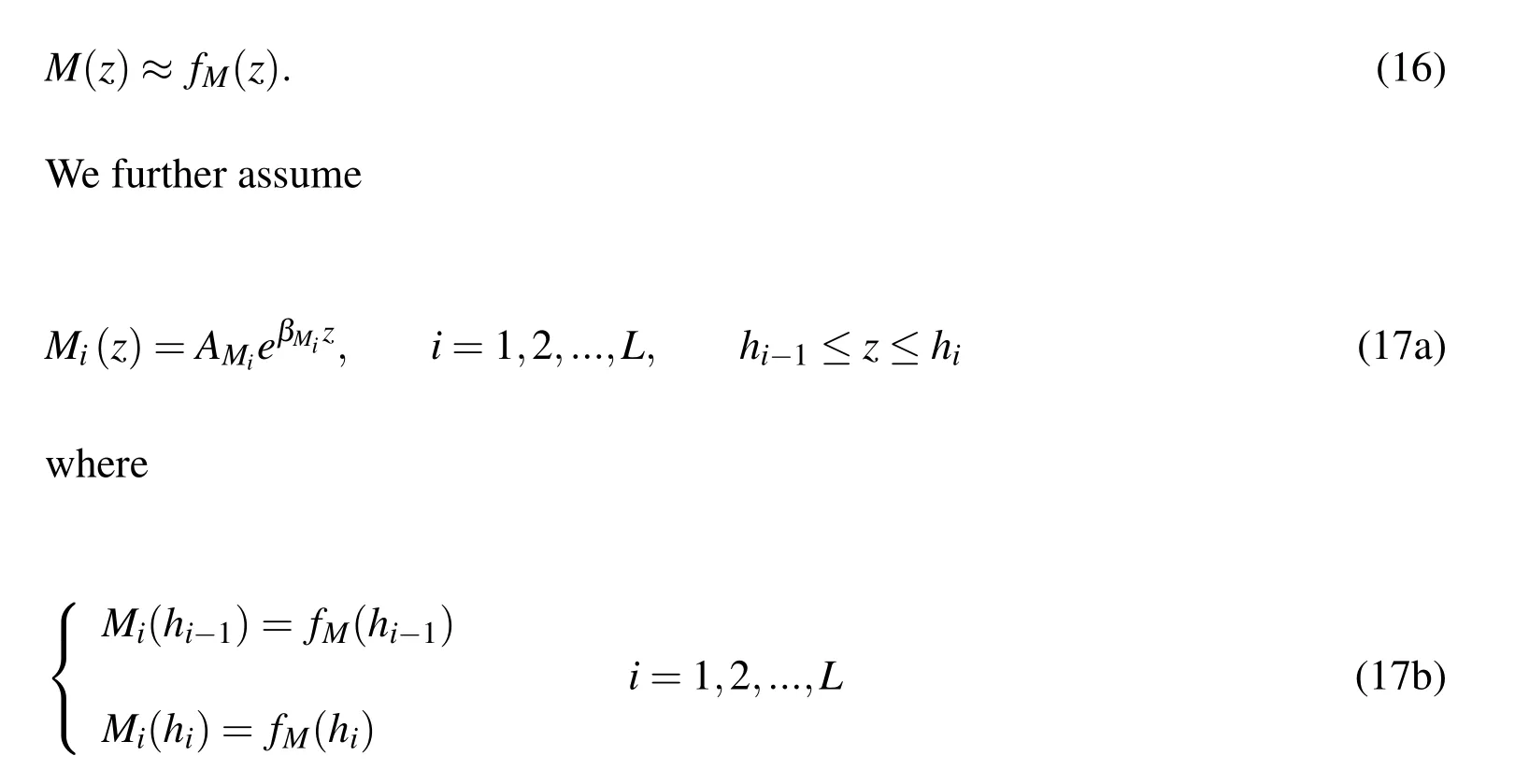
Given a set of actual values of a thermal/mechanical property,fM(hi),i=1,2,...,L,for each segmentAMiandBMican be solved from Eqs.(17a,b)as

whereMcan be replaced respectively with the Young’s modulusE,the coefficient of thermal expansion α ,thermal conductivity λ ,and yield stress σ0y,etc.,therefore,

Considering that the variation of the Poisson’s ratio in each layer is insignificant and in order to simplify the analysis,we assume the Poisson’s ratio in each layer is a constant taking the mean of the Poisson’s ratio over the thickness,i.e.,

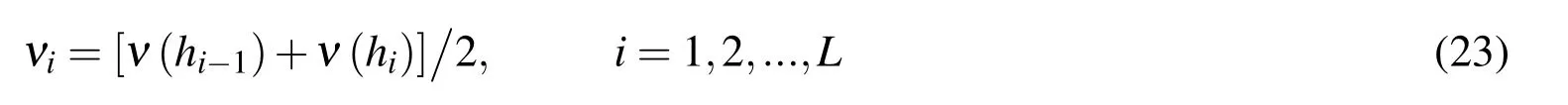
If the volume fraction of particles athiis ξ (hi),thenfE(hi),fα(hi)andfλ(hi)can be obtained as[Juet al.(1994);Shen(1998)]

Here the subscript“m”and “c”denote matrix and inclusion,respectively;Km,KcandKare the bulk moduli of the matrix,the inclusion,and the composite,respectively;µm,µcand µ are shear moduli of the matrix,the inclusion,and the composite,respectively.

Combining the mean field scheme[Juet al.(1994)]and the constitutive model mentioned in section 2,one can obtainfy(hi).

3.3 Distribution of temperature

Assuming steady-state heat transfer,the distribution of the temperature in a structure can be described with the following equation of heat conduction,without considering source heat,

For uniaxial heat transfer,as shown in Figure 3,Eq.(32)can be simplified as

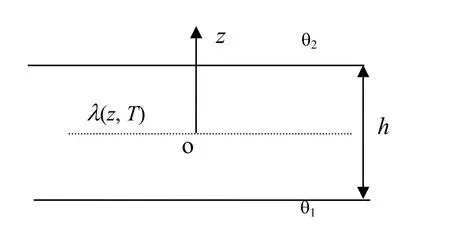
Figure 3:Heat tran ree plate

Making the boundary condition shown in Figure 3,we obtain

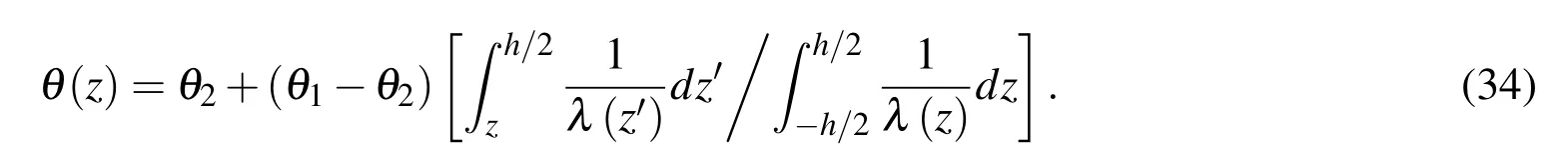
Letting∆˜θ=θ1-θ2,∆θ(z)=θ(z)-θ2,Eq.(34)can rewritten as

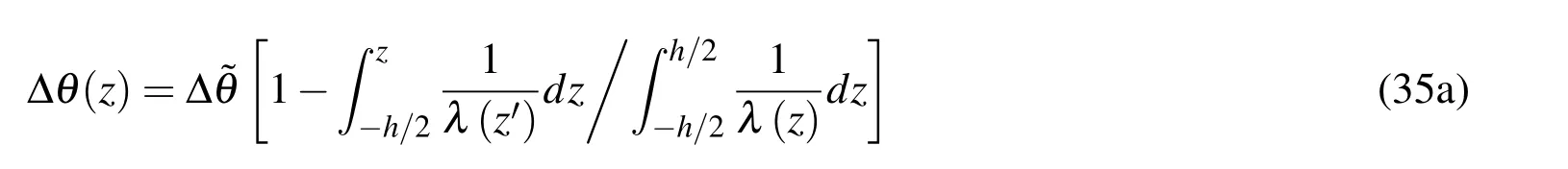
For the distribution of the temperature in the Bree plate shown in Figure 1,

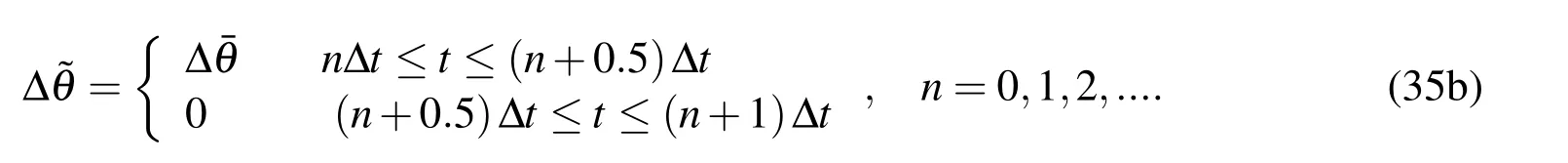
Substituting Eq.(21)into Eq.(35a),there have been

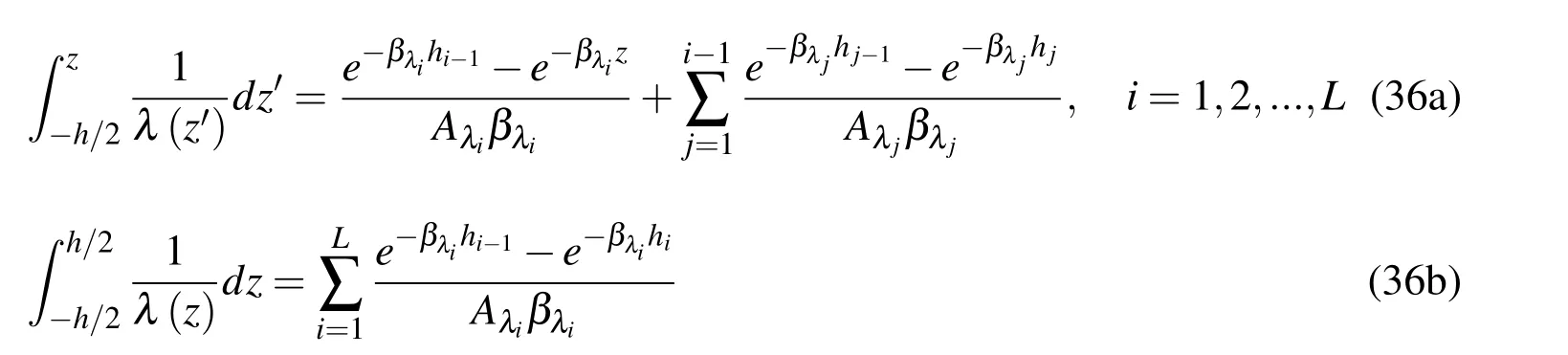
And then∆θi(z)can be obtained as

Here

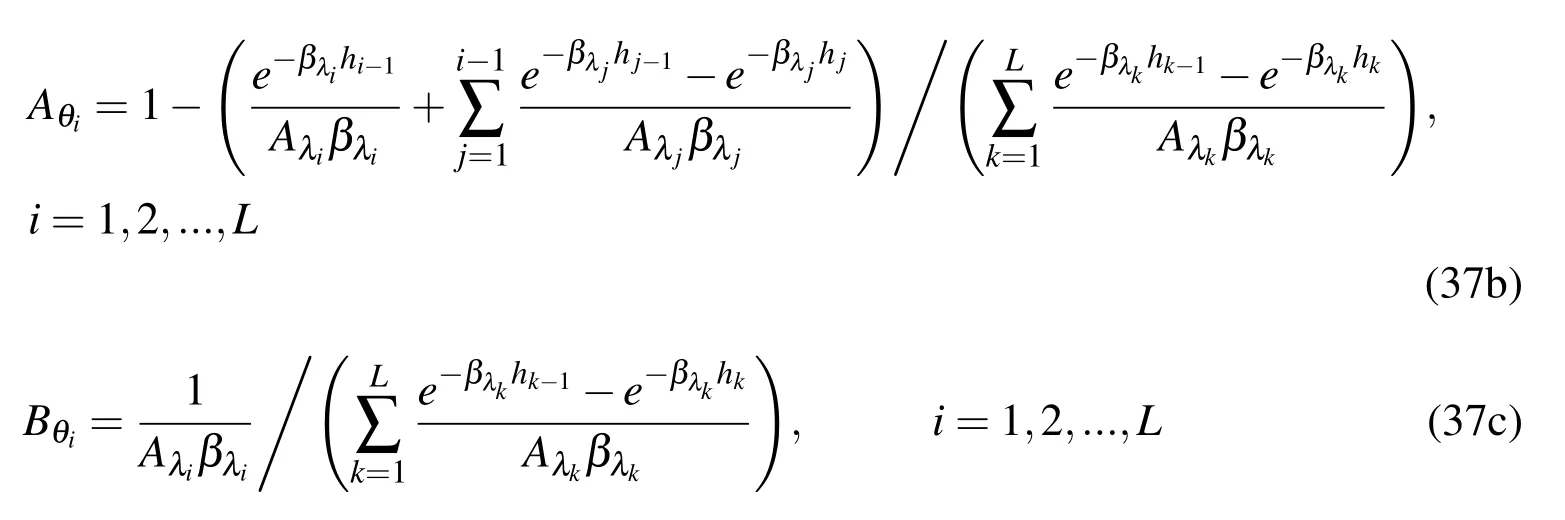
3.4 Purely elastic solution

For the FG Bree plate,we will be concerned with the solution when the displacement iny-direction is fixed,i.e.,εy=0,for simplicity.In this case,we need not be concerned with the yield condition iny-direction[Bree(1967)].The components of the strain in the plate subjected to stress σx,σycan be expressed as

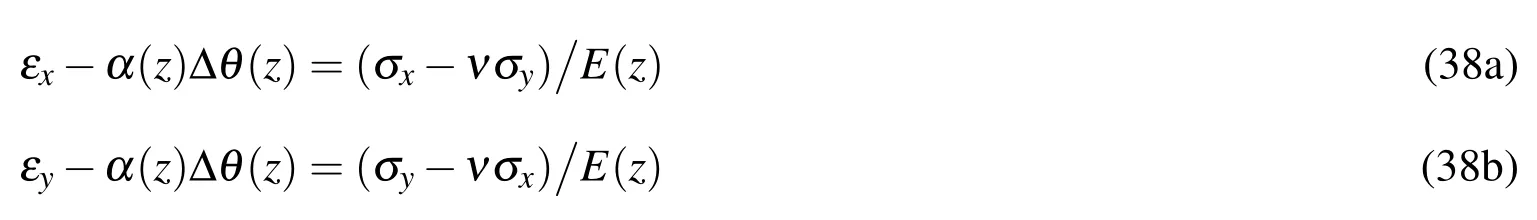
where ∆θi(z)is the temperature change atz.Keeping in mind that εy=0,it can be solved from Eq.(38)that

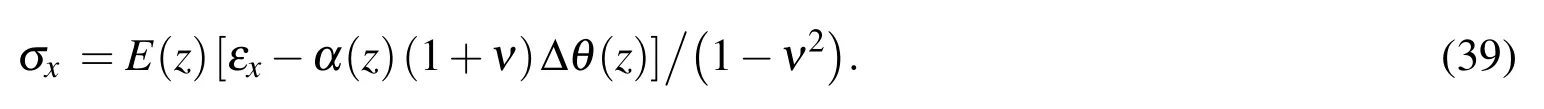
(1)Purely elastic solution of the stress distribution σPcaused byPx

WhenPxis applied individually,i.e.,∆θ(z)=0,the equilibrium inx-direction gives

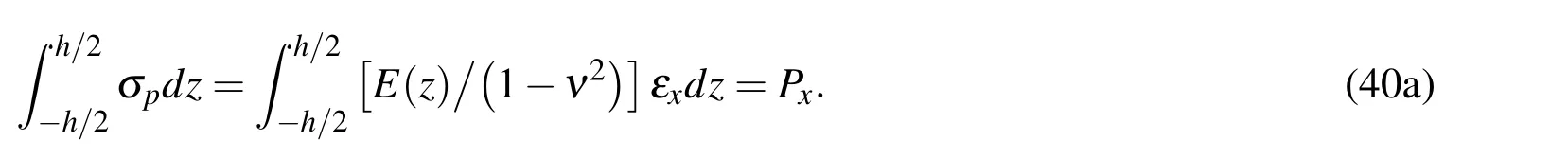
Substituting Eq.(39)and∆θ(z)=0 into Eq.(40a),one obtains

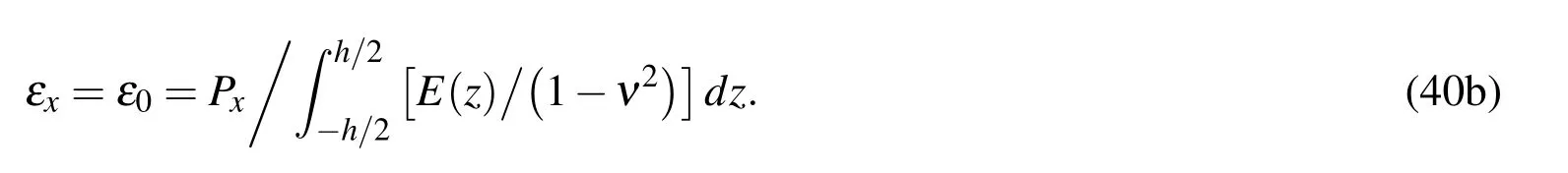
Keeping in mind that ν is treated as a constant(Eq.(23))and using Eq.(39),we obtain the purely elastic solution of the stress distribution σpcaused byPxas

Making use of the PWED model,the denominator on the RHS of Eq.(41a)can further be expressed as

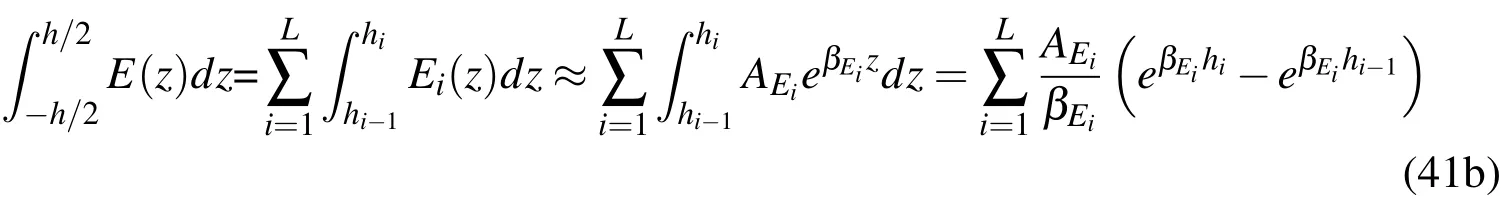
Thus,Eq.(41a)can be expressed in the following discrete form

(2)Purely elastic solution of the stress distribution σθcaused by∆¯θ

When∆¯θ is applied individually,one has the following condition of equilibrium

Keeping in mind that

And substituting Eq.(39)into Eq.(43)yields

Combining Eq.(45)with Eq.(39),the distribution of the thermal stress can be determined as

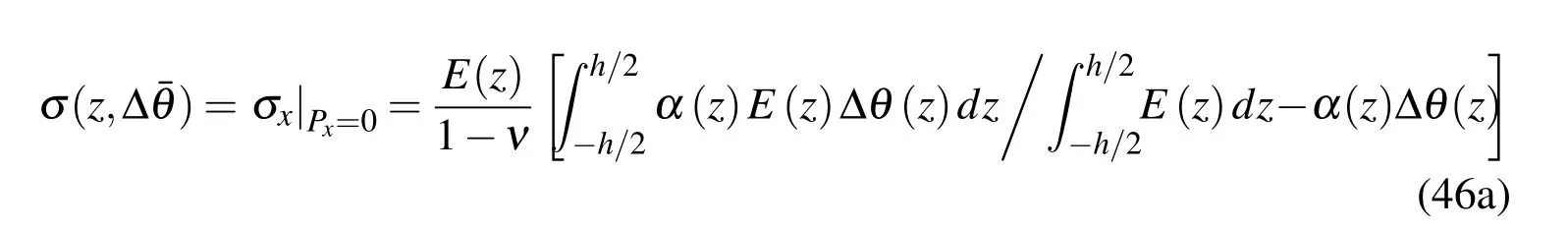
Making use of the PWED model,we obtain the following discrete form

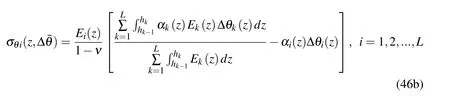
Substituting Eqs.(19)-(21)and Eq.(37a)into Eq.(46b),we can obtain

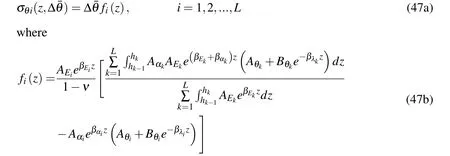
Compared with Eq.(43),there isHere,the fi rst term in the square bracket on the right side of Eq.(47b)can be expressed as

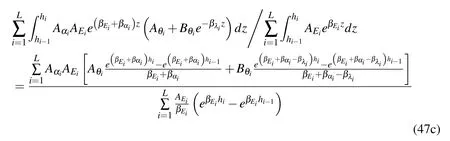
3.5 Static shakedown analysis

The analysis for the shakedown of the Bree plate includes the determination of the boundary of initial yield,the boundary between the areas of shakedown and incremental collapse,and the boundary between the areas of shakedown and reversed plasticity.

The plate contains two parts,in one partfi(z)≤0 and in the other partfi(z)≥0.For the thermal and mechanical loading shown in Figure 1,we can obtain the following shakedown boundaries.

(1)Initial yield

No plastic deformation takes place on the condition that

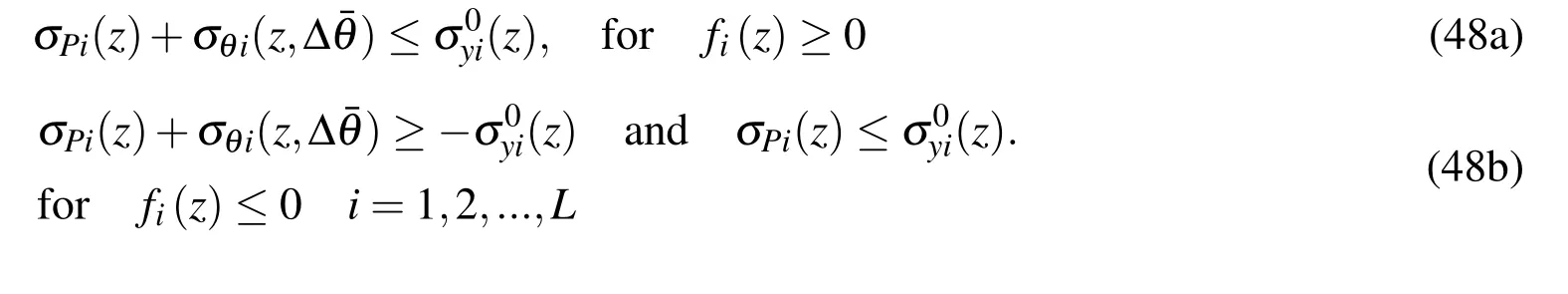
(2)Static shakedown boundaries

Suppose there are a time-independent residual stress field ρ¯xi(z)and a time-independentfieldk∗(1 ≤k∗≤d),the shakedown will occur to the plate if the following condition is satisfied in one temperature change cycle

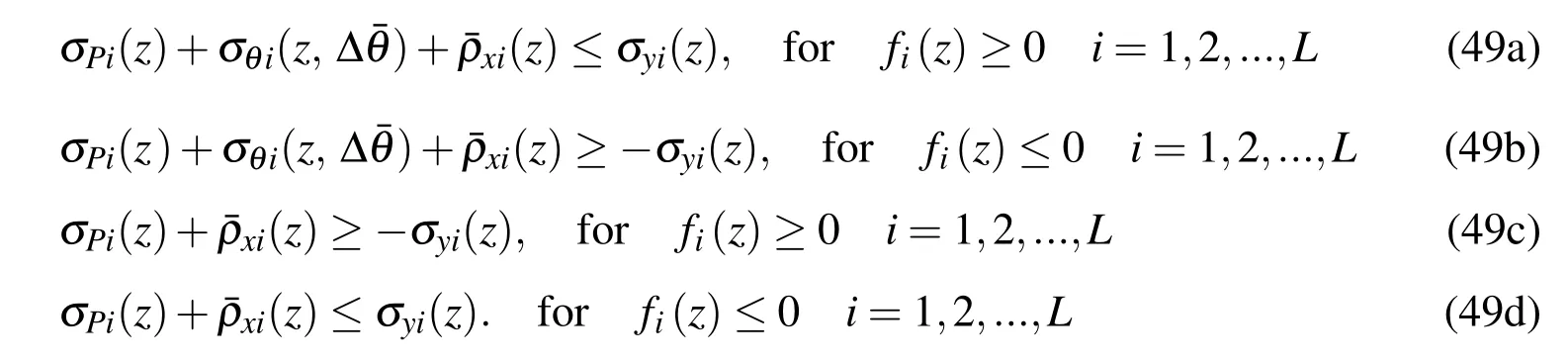
where σyi(z)=k*σ0yi(z)andk*=d.

The shakedown boundaries of the plate contain two parts:the boundary between the area of shakedown and that of incremental collapse,and the boundary between the area of shakedown and that of reversed plasticity.

(a)Shakedown boundary corresponding to reversed plasticity

It can be obtained fromIneq.(49)that

The equality of both sides of anyone in Ineq.(50)at any point in the cross section implies the equality of both sides of Ineqs.(49a)and(49c),or the equality of Ineqs.(49b)and(49d),indicating that reversed plasticity occurs at this point in the cross section.

(b)Shakedown boundary corresponding to incremental collapse

Making use of the given time-independent residual stress field¯ρxi(z)and noticing that∆˜θ=∆¯θ asn∆t≤t≤(n+0.5)∆t,Ineqs.(49a,b)can be rewritten in this duration as

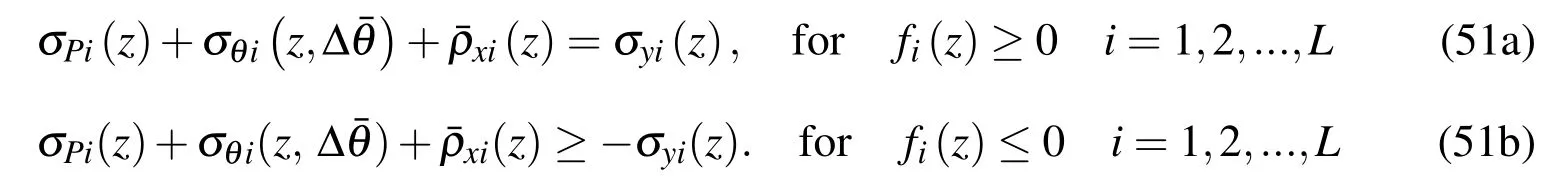
Since∆˜θ=0 as(n+0.5)∆t≤t≤(n+1)∆t,in this duration Ineqs.(49c,d)will be reduced to

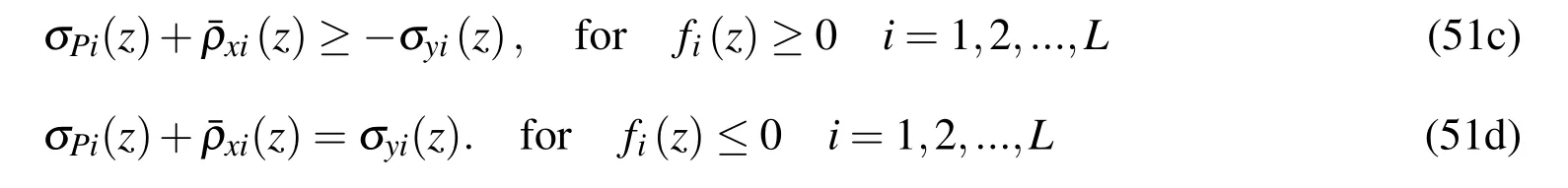
Ineq.(51)indicates that at each point in the region wherefi(z)≥0 of the cross section,the stress σ+=σPi(z)+σθi(z,∆¯θ)+¯ρxi(z)reaches σyi(z);while at each point in the region wherefi(z)≤ 0 of the cross section,the stress σ-= σPi(z)+¯ρxi(z)reaches σyi(z).That is,duringn∆t≤t≤(n+0.5)∆t,σ+in a part of the Bree plate reaches σyi(z),and during(n+0.5)∆t≤t≤ (n+1)∆t,σ-at the in the rest part of the Bree plate reaches σyi(z).The two parts of the cross section may flow forward alternatively.

3.6 Objective of optimization

To theorize objective function is the key in GA approach.In this paper the objective of the optimization is the maximization of∆¯θ in the FG Bree plate under the condition of shakedown.The temperature∆¯θ can be solved from Ineqs.(50a,b)and Eq.(47a)as

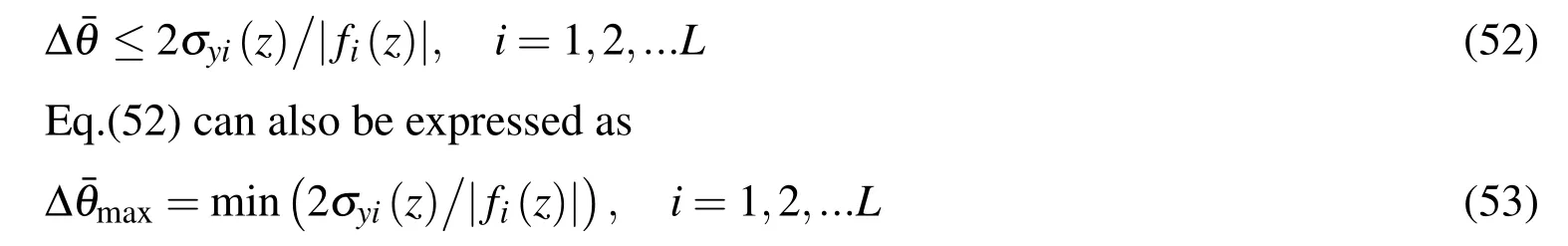
The objective of the optimization is to find∆¯θmax.

3.7 Variables and constraint of optimization

The objective to be optimized is the distribution of volume fraction of the reinforcement particles in a FG Bree plate.The distribution function is assumed as

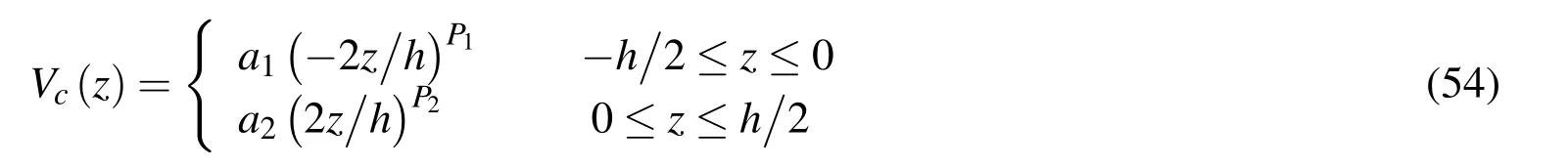
whereh=60mm is the thickness of the plate,and the variables to be optimized are

a1,a2,P1andP2.The boundaries of these variables are assumed as

Opt_0.3:a1,a2∈[0.0,0.3];P1,P2∈[0.0,2]

Opt_0.4:a1,a2∈[0.0,0.4];P1,P2∈[0.0,3]

Opt_0.5:a1,a2∈[0.0,0.5];P1,P2∈[0.0,3]

The constraint to the optimization is that the gross volume fraction of the reinforcement particles in the plate is 15%,i.e.,

The shakedown of the plate is determined with Ineqs.(48)-(51),and the best distribution of the volume fraction of the reinforcement particles is obtained by optimization calculation.

3.8 Computing process of GA approach

In this paper,the fi rst important thing is to program subroutines in matlab language about the constraint function and the fitting function which is related to the objective function.The computer process of the optimization is depicted in Figure 4.

The parameters in GA approach are given as follows.The population type is double vector and the population size is 100.The numerical value of generations is 100.The crossover fraction is 0.8 and mutation fraction is 0.01.The constraint function is solved by penalty function method and the penalty factor is 100.

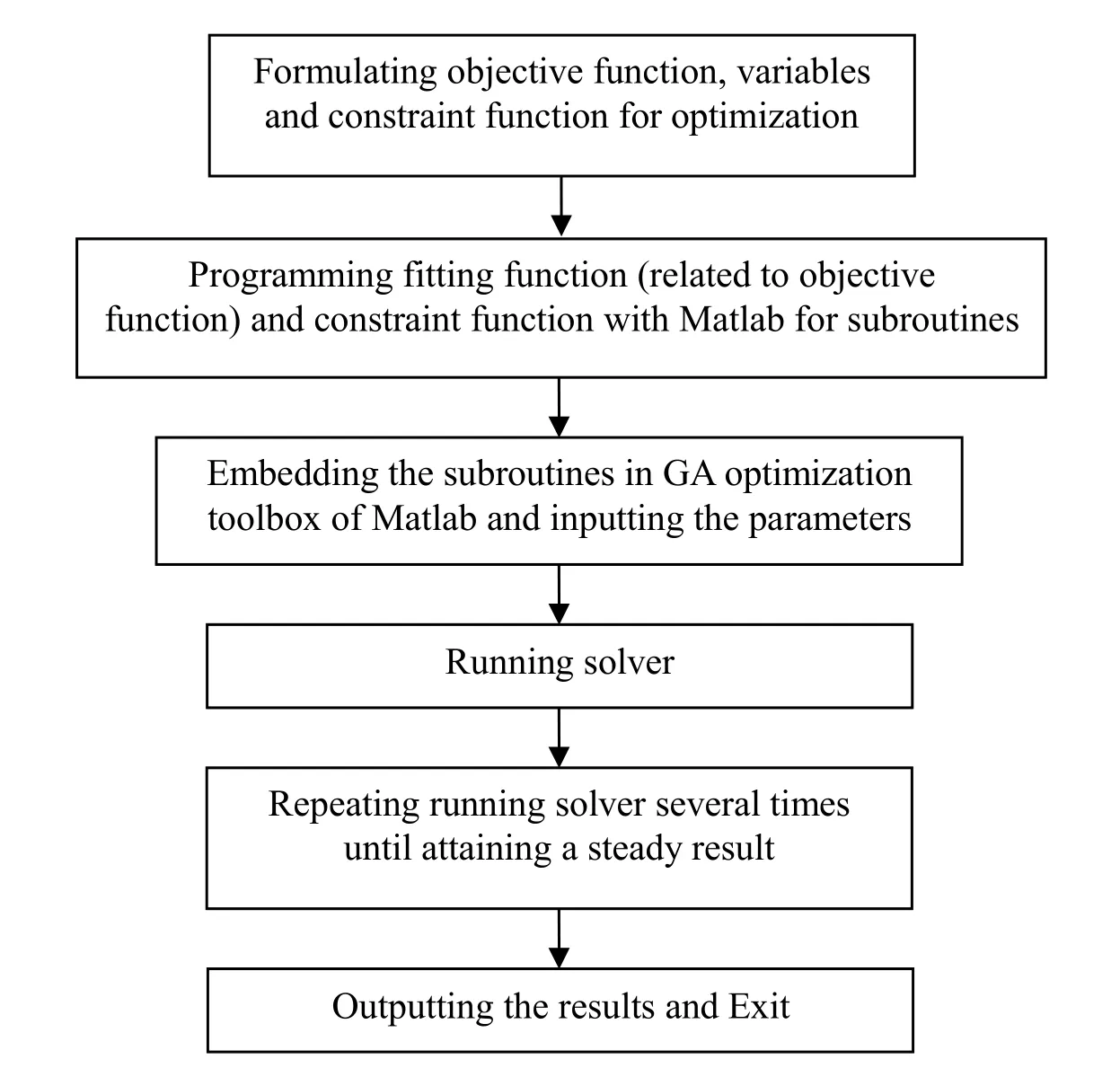
Figure 4:Computer process of the optimization.

4 Numerical examples

4.1 Optimal design of Al/SiC FG Bree plate

The first example is the optimization of an Al/SiC FG Bree plate.The reinforcement phase is SiC,and the total volume fraction of the SiC particles keeps 15%in the optimization process.The material properties of Al and SiC[Shen(1998)]are listed in Table 1.

Table 1:Material properties of Al and SiC.

The optimal design results of the Al/SiC FG plate are

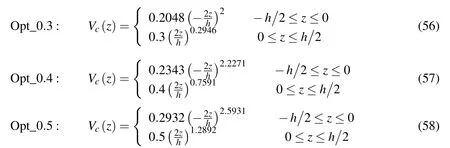
The shakedown boundaries of Al/SiC FG Bree plates,with the volume fraction distribution functions of the SiC particles given above,are shown in Figure 4 with the curves marked with curve Opt_0.3,curve Opt_0.4 and curve Opt_0.5,respectively.For comparison,the shakedown boundaries of the Al/SiC FG plates with the volume fraction distribution functions given in Eqs.(59)-(61)are also shown in Figure 4,respectively,denoted as Linear 1,Linear 2 and Homo_0.15.

The distributions of the stress in the plates corresponding to points E1through E6are shown in Figures 6-11,respectively,where¯ρxdenotes the residual stress,σθthe thermal stress,σPthe mechanical stress, σythe yield strength,σ+the stress σθ+σP+¯ρxand σ-the stress σP+¯ρxin the plates.

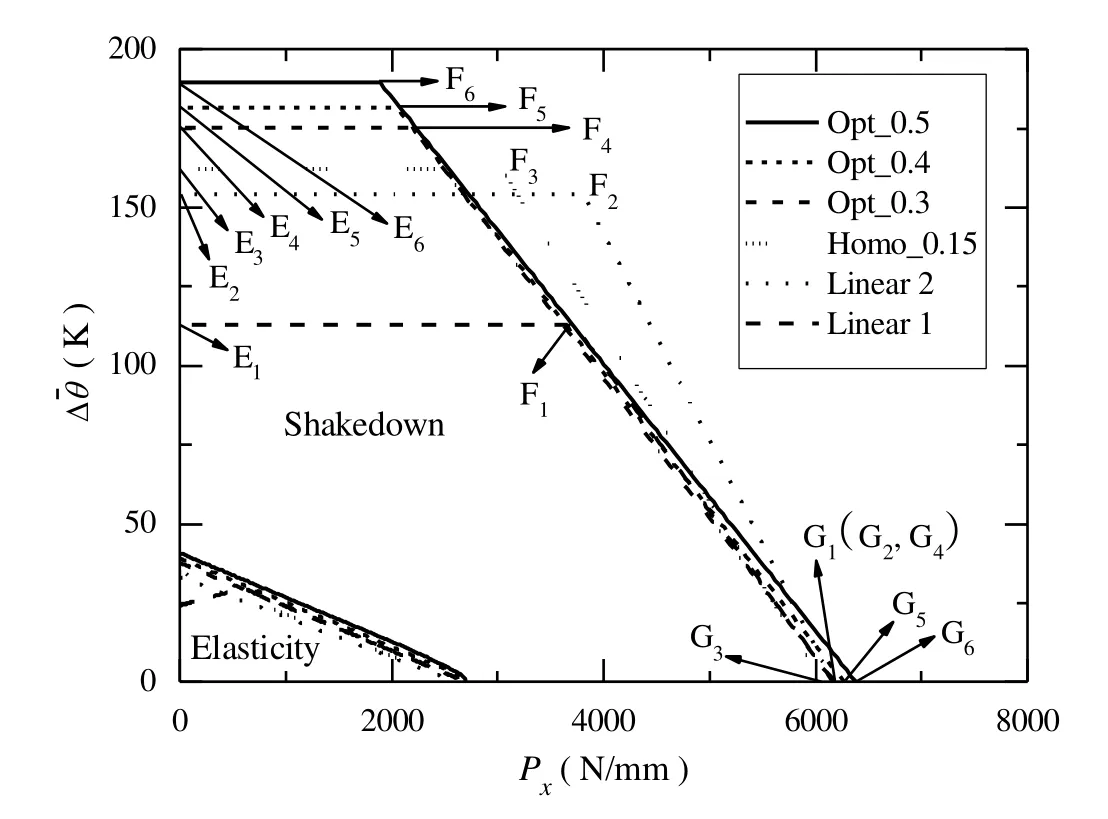
Figure 5:Shakedown area of different Al/SiC FG Bree plate after optimization.

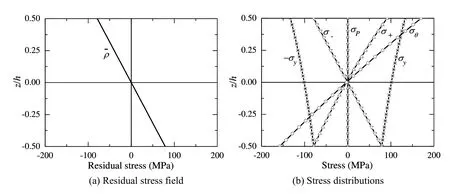
Figure 6:Stress distributions in Al/SiC FG plate corresponding to point E1.

Figures 6 and 7 show respectively the stress distributions in the Al/SiC FG plates corresponding to the points E1(withVcdetermined by Eq.(59))and E2(withVcdetermined by Eq.(60))in Figure 5.It can be seen in Figure 5 that the∆¯θ at E2is larger than that at E1.The comparison between the stress distributions shown in Figures 6 and 7 indicates that the difference in∆¯θ can be attributed to the difference between the distributions of stress,and the difference between the material properties,for example,the yield strength.One can find in Figure 6 that,the weakest point where both σ+and σ-reach the yield strength,is located at the lower surface of the plate,where the yield strength of the material is the lowest.While in Figure 7 the weakest point, where bothσ+andσ-reach the yield strength,is located at the upper surface of the plate,where the yield strength of the material is the lowest.

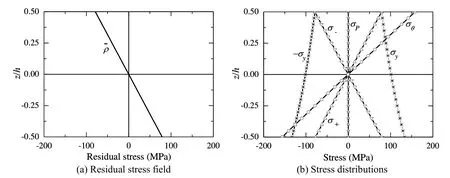
Figure 7:Stress distributions in Al/SiC FG plate corresponding to point E2.

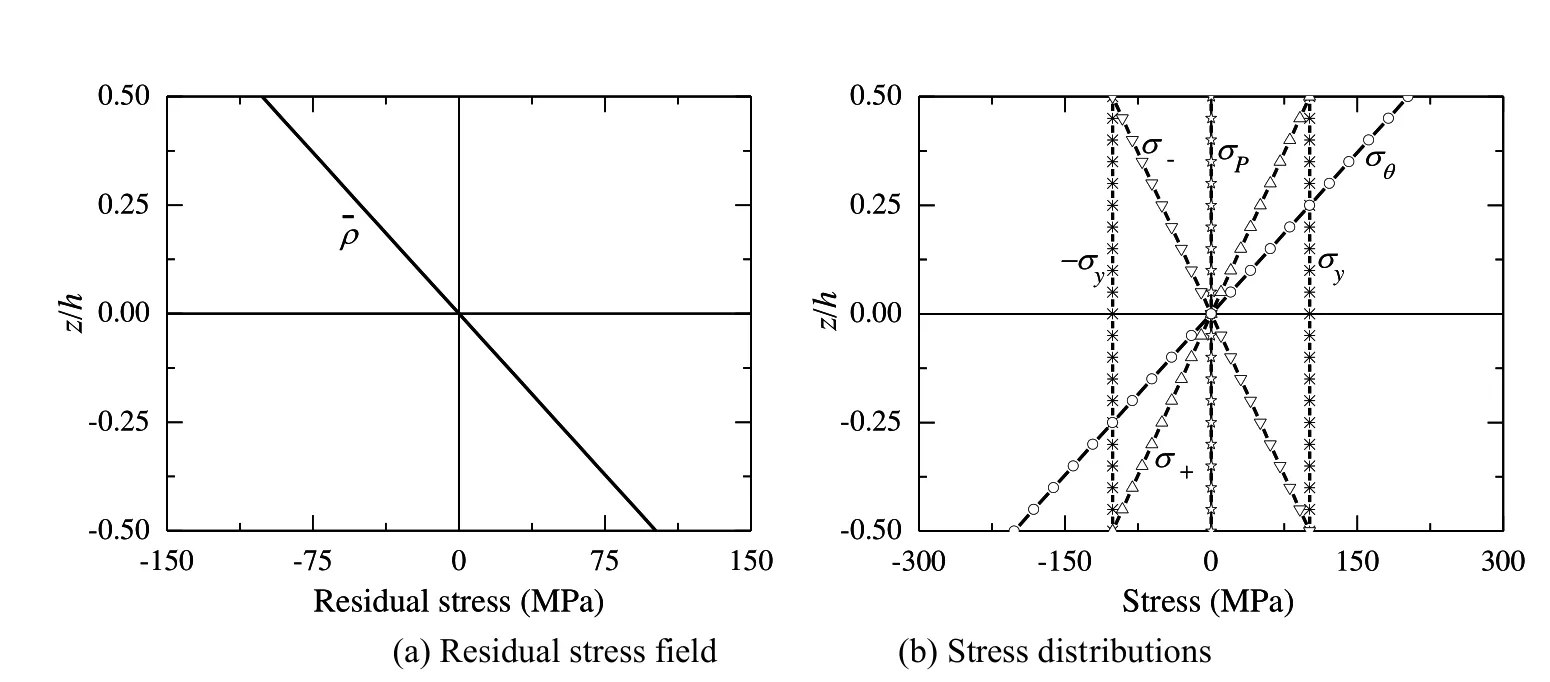
Figure 8:Stress distributions in Al/SiC effective homogeneous plate corresponding to point E3.

The stress distributions in the plate,corresponding to the point E3on the curve marked with Homo_0.15(Figure 5)are shown in Figure 8,in which the SiC particles distribute uniformly withVc=0.15(Eq.(61)).It can be seen that for the residual stress fi eld shown in Figure 8(a),the obtained σ+and σ-reach the yield strength at both the upper and the lower surfaces.The corresponding∆¯θ(Figure 5)is a little larger than that corresponding to E2.The comparison between the results corresponding to points E1,E2and E3implies the possibility to achieve a better shakedown boundary by optimizing the distribution of the material properties with a proper distribution of particle volume fraction.

The optimized shakedown boundary corresponding to the distribution of Eq.(56)is given in Figure 5 with the curve marked with Opt_0.3.Given the residual stress field shown in Figure 9(a),the stress distributions at point E4are shown in Figure 9(b),where it can be seen that reversed plastic deformation takes place at both the upper and the lower surfaces.Compared with the result at either E1,E2or E3,the∆θ¯ at E4of Opt_0.3 increases to some extent.

Figure 9:Stress distributions in Al/SiC FG plate corresponding to point E4.

The optimized shakedown boundary corresponding to the distribution of Eq.(57)is given in Figure 5 with the curve marked with Opt_0.4.Given the residual stress field shown in Figure 10(a),the stress distributions at point E5are shown in Figure 10(b),where it can be seen that reversed plastic deformation takes place at both the upper and the lower surfaces.Compared with the result at E4,the∆θ¯ at E5in the curve marked with Opt_0.4 increases,which could be attributed to that the maximum particle volume fraction at the upper surface is increased from 0.3 to 0.4,which enhances the capability of the plate to bear the thermal loading.

The optimized shakedown boundary corresponding to the distribution of the particle volume fraction of Eq.(58)is given in Figure 5 with the curve marked with Opt_0.5.Given the residual stress field shown in Figure 11(a),the stress distributions at point E6are shown in Figure 11(b),where it can be seen that reversed plastic deformation takes place at both two surface(one is the upper surface,the other one is not the lower surface but a little higher than it).Compared with the result at E5,the∆¯θ at E6in the curve marked with Opt_0.5 further increases,which could be attributed to that the maximum particle volume fraction at the upper surface is increased from 0.4 to 0.5,which further enhances the capability of the plate to bear the thermal loading.

The comparison between the∆¯θ at the points E1through E6in Figure 5 shows that the∆¯θ at E6,corresponding to the distribution of the particle volume fraction,Eq.(58),is the largest.If the maximum particle volume fraction is limited to 0.5,this∆¯θ can be regarded as∆¯θmax.

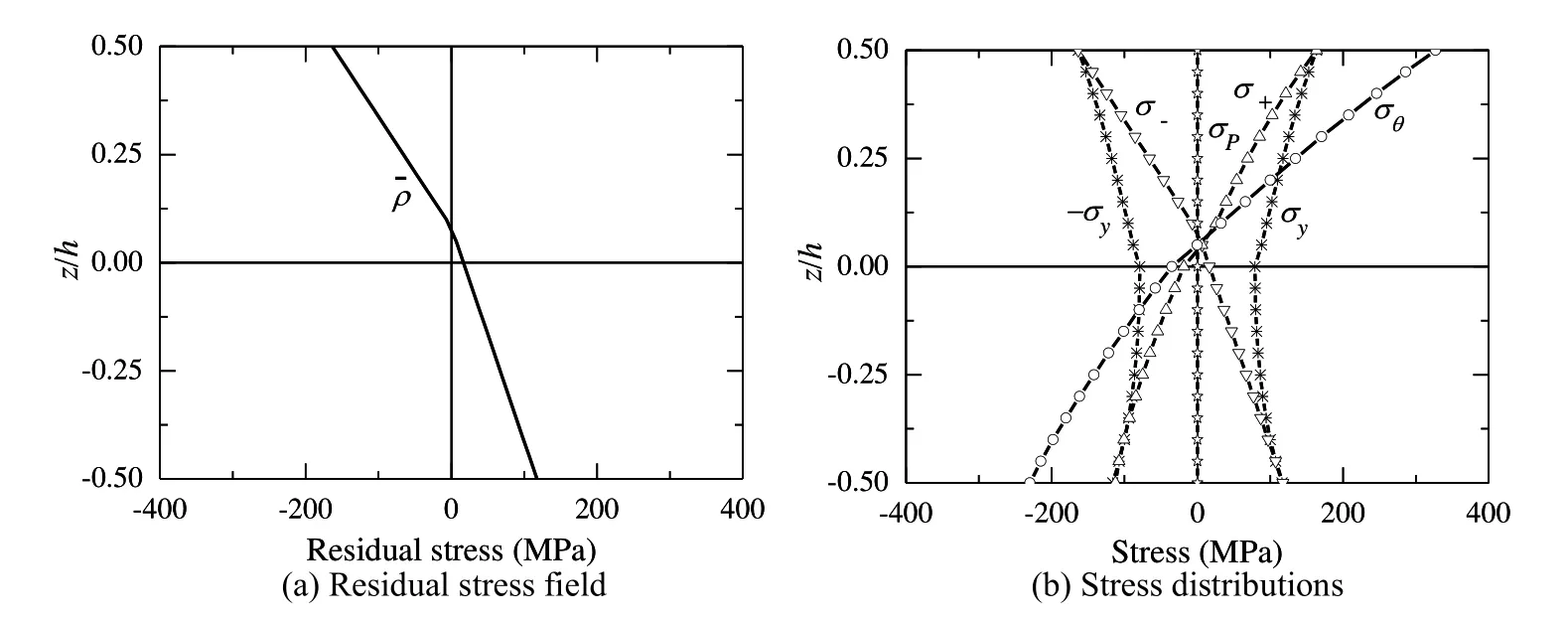
Figure 10:Stress distributions in Al/SiC FG plate corresponding to point E5.

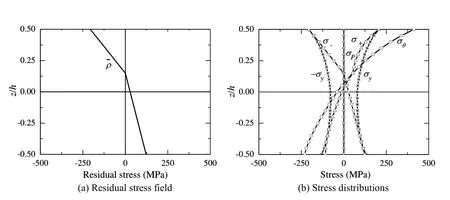
Figure 11:Stress distributions in Al/SiC FG plate corresponding to point E6.

4.2 Optimal design of Ti/Si3N4FG Bree plate

In order to further verify the optimal design model,the optimization for shakedown capability of a Ti/Si3N4FG Bree plate is performed,in which the Si3N4particles are the reinforcement phase.Material constants of Ti and Si3N4[Cho et al.(2004)]are listed in Table 2.

We also assume three classes of the Ti/Si3N4FG Bree plates,of which the distribution of the Si3N4particle volume function is described with Eq.(54),wherea1,P1anda2,P2are the parameters to be optimized.If the average particle volume is limited to 0.15,and the maximum local particle volume fractions of the three classes are 0.3(Class 1),0.4(Class 2)and 0.5(Class 3),respectively,the corresponding shakedown boundaries are shown in Figure 12 with the curves marked with Opt_0.3,o Opt_0.4 and Opt_0.5,respectively.With the optimizeda1,P1anda2,P2,the three classes distribution functions can be expressed as

Table 2:Material constants of Ti and Si3N4.

For comparison,the shakedown boundaries of Ti/Si3N4FG plates with the particle volume fraction distribution functions of Eqs.(59)-(61)are also given in Figure 12 with the curves marked with Linear 1,Linear 2 and Homo_0.15 respectively.

Figure 13 show the stress distributions in the FG plate corresponding to point E1on the curve marked as Linear 1 in Figure 13.Figure 14 shows the stress distributions in the FG plate corresponding to point E2on the curve marked as Linear 2 in Figure 11.The results shown in Figure 13 and Figure 14 are respectively similar to that in Figure 6 and Figure 7.

Then,the shakedown of the equivalent homogenous plate is analyzed in the same way as numerical example 1,and the boundary which is marked as Homo_0.15 is shown in Figure 12.Stress distributions corresponding to point E3are shown in Figure 15.

Be similar to the numerical example of Al/SiCFG plate,the optimization of Ti/Si3N4FG plate is given.The results of optimal volume fraction distribution functions of Si3N4have been given as Eqs.(62)-(64),and the shakedown boundaries of corresponding FG plates have been shown as Opt_0.3,Opt_0.4 and Opt_0.5 in Figure 12.As shown in Figure 12,the plate of which the reinforcement phase volume fraction function is optimized can be endured larger∆¯θmax,i.e.,∆¯θmaxof whichever Opt_0.3,Opt_0.4 and Opt_0.5 is larger than that of Homo_0.15.

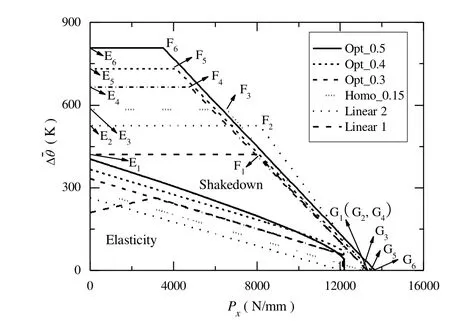
Figure 12:Shakedown area of different Ti/Si3N4FG Bree plate after optimization.

Figure 13:Stress distributions in Ti/Si3N4FG plate corresponding to point E1.

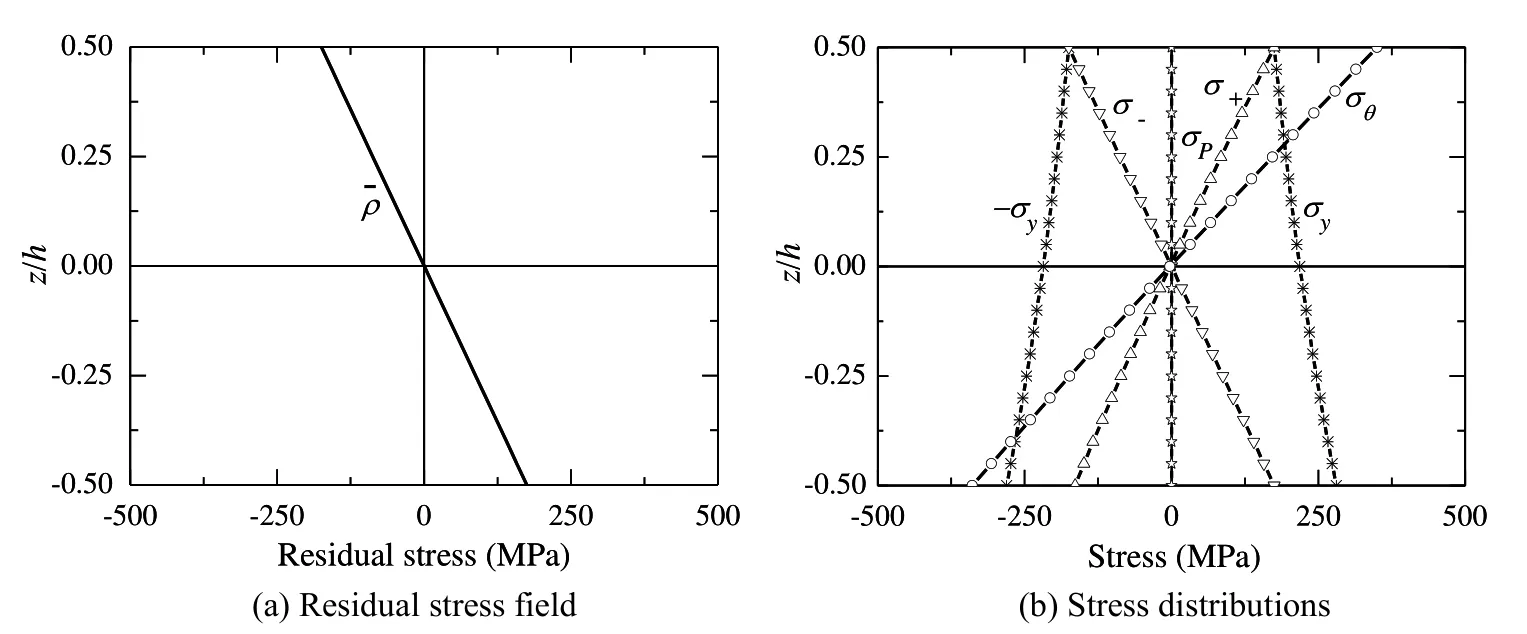
Figure 14:Stress distributions in Ti/Si3N4FG plate corresponding to point E2.

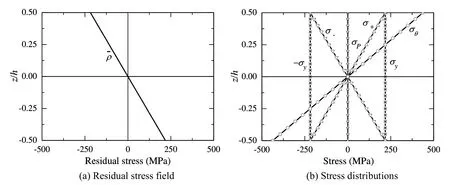
Figure 15:Stress distributions in Ti/Si3N4effective homogenous plate corresponding to point E3.

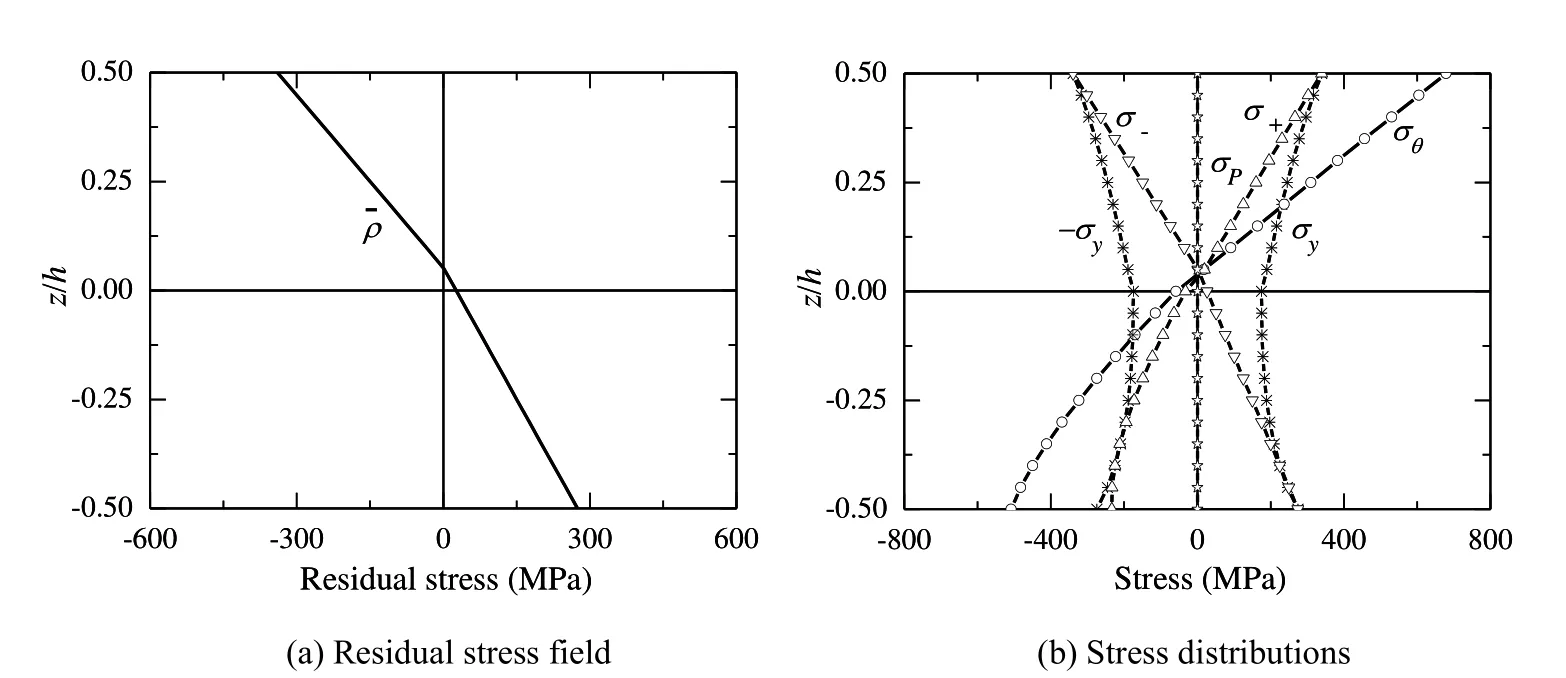
Figure 17:Stress distributions in Ti/Si3N4FG plate corresponding to point E5.

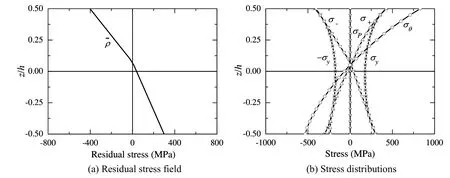
Figure 18:Stress distributions in Ti/Si3N4FG plate corresponding to point E6.

The stress distributions corresponding to point E4on Opt_0.3,point E5on Opt_0.4 and point E6on Opt_0.5 have been respectively shown in Figures 16-18.In these figures the phenomena are similar with those in Figures 9-11,although the constituents of the FG plates are different.

5 Conclusion and discussion

The optimization of the volume fraction distribution function of reinforcement particles in FG Bree plates was performed with the GA approach.The objective of optimization was to gain the maximum of the∆¯θ applied to the plates under the constraint that the average volume fraction of the reinforcement particles keeps constant.An optimal model was proposed and two numerical examples were presented,from which the following conclusion may be drawn:

1.An approach was developed for the optimization of the distribution of the reinforcement particles in the plate for the purpose to enhance the shakedown capability of the plate.The distribution of the material properties in the thickness of the plate was characterized with a piecewise exponential distribution,and the effective mechanical property of the material of the plate was evaluated with a double-inclusion mean fi eld scheme,and the distribution of the volume fraction of the reinforcement particles was optimized with the Genetic Algorithm.The validity of the approach was demonstrated by the two numerical examples.

2.The shakedown capability of a FG plate is determined by both the applied thermal-mechanical loading and the thermal-mechanical properties of the plate.For a FG plate,the latter can be designed by properly distributing the volume fraction of the reinforcement particles,which provides the possibility to achieve desired or optimal thermal-mechanical properties of the plate to substantially enhance the shakedown capability of the plate.It was found in this paper that the distribution of the particle volume fraction affects markedly the shakedown capability of the FG plate,and a proper distribution of the particle volume fraction can substantially enhance the shakedown capability of the plate.

3.The concept of the piecewise distribution of the material properties is in accordancewith that of the piecewise approach used in the shakedown analysis;therefore,it is of particular advantage for the optimization of the shakedown capability of the FG plate,because it may bring great convenience to the optimization without introducing additional difficulties.

Acknowledgement:The authors gratefully acknowledge the financial support to this work from NSFC under Grant Numbers 11272364 and 11332013.

Andrew,J.G.;Senthil,S.V.(2010):Transient multiscale thermoelastic analysis of functionally graded materials.Compos.Struct.,vol.92,pp.1372-1390.

Aghababaei,R.;Reddy,J.N.(2009):Nonlocal third-order shear deformation plate theory with application to bending and vibration of plates.J.Sound Vib.,vol.326,pp.277–289.

Altenbach,H.;Eremeyev,V.A.(2009):Eigen-vibrations of Plates made of Functionally Graded Material.CMC:Computers,Materials,&Continua,vol.9,pp.153-178.

Bree,J.(1967):Elastic plastic behavior of thin tubes subjected to internal pressure and intermittent high heat fluxes with application to fast nuclear reactor fuel elements.J.Strain Anal.,vol.2,pp.226-238.

Cavalcanti,P.R;Carvalho,P.C.P;Martha,L.F.(1997):Non-manifold modeling:an approach based on spatial subdivision.Computer-Aided Design,vol.29,pp.209-220.

Chen,B.;Tong,L.(2005):Thermo-mechanically coupled sensitivity analysis and design optimization of functionally graded materials.Comput.Methods Appl.Mech.Eng.,vol.194,pp.1891-1911.

Chen,M.;Tucker,J.V.(2000):Constructive volume geometry.Comput.Graph.Forum,vol.19,pp.281-293.

Cheng,Z.Q.;Batra,R.C.(2000):Three-dimensional thermoelastic deformations of a functionally graded elliptic plate.Composites Part B,vol.31,pp.97-106.

Cho,J.R.;Choi,J.H.(2004):A yield-criteria tailoring of the volume fraction in metal-ceramic functionally graded material.Euro.J.Mech./A Solids,vol.23,pp.271-281.

Cho,J.R.;Ha,D.Y.(2002):Volume fraction optimization for minimizing thermal stress in Ni–Al2O3functionally graded materials.Mater.Sci.Eng.A,vol.334,pp.147–155.

Cho,J.R.;Shin,S.W.(2004):Material composition optimization for heat-resistingFGMs by artificial neural network.Composites Part A:Applied Science and Manufacturing,vol.35,pp.585–594.

Dong,L.;Atluri,S.N.(2012a):T-Trefftz voronoi cell fi nite elements with elastic/rigid inclusions or voids for micro mechanical analysis of composite and porous materials.CMES:Computers,Materials,&Continua,vol.83,pp.183-219.

Dong,L.;Atluri,S.N.(2012b):Development of 3D Trefftz voronoi cells with ellipsoidal voids&/or elastic/rigid inclusions for micro mechanical modeling of heterogeneous materials.CMC:Computers Materials and Continua,vol.30,pp.39-81.

Dong,L.;Atluri,S.N.(2013):SGBEM voronoi cells(SVCs),with embedded arbitrary-shaped inclusions,voids,and/or cracks,for micro mechanical modeling of heterogeneous materials.CMC:Computers,Materials&Continua,vol.33,pp.111-154.

Elishakoff,I.;Gentilini,C.(2005):Three-dimensional flexure of rectangular plates made of functionally graded materials.J.Appl.Mech.,vol.72,pp.788-791.

Feldoman,E.;Aboudi,J.(1997):Buckling analysis of functionally graded plates subjected to uniaxial loading.Compos.Struct.,vol.38,pp.29-36.

Guo,L.C.;Noda,N.(2007):Modeling method for a crack problem of functionally graded materials with arbitrary properties piecewise exponential model.Int.J.Solids Struct.,vol.44,pp.6768-6790.

Guo,L.;Wu,L.;Sun,Y.;Ma,L.(2005):The transient fracture behavior for a functionally graded layered structure subjected to an in-plane impact load.Acta Mech.Sinica,vol.21,pp.257-266.

Gilhooley,D.F.;Batra,R.C.;Xiao,J.R.;Mccarthy,M.A.;Gillespie,J.W.(2007):Analysis of thick functionally graded plates by using higher-order shear and normal deformable plate theory and MLPG method with radial basis functions.Compos.Struct.,vol.80,pp.39-552.

Huang,J.;Fadel,G.M;Blouin,V.Y;Grujicic,M.(2002):Bi-objective optimization design of functionally gradient materials.Materials and Design,vol.23,pp.657-666.

Ju,J.W.;Chen,T.M.(1994):Micro mechanics and effective moduli of elastic composites containing randomly dispersed ellipsoidal inhomogeneities.Acta Mech.,vol.103,pp.103-121.

Khalil,S.;Nam,J.;Darling,A.;Sun,W.(2004):Multi-nozzle biopolymer deposition for freeform fabrication of tissue construct.In:Proc.15th solid freeform fabrication symposium,pp.826-837.

Kou,X.Y.;Parks,G.T.;Tan,S.T.(2012):Optimal design of functionally graded materials using a procedural model and particle swarm optimization.Computer-Aided Design,vol.44,pp.300-310.

Kou,X.Y.(2006):Computer-aided design of heterogeneous objects.Ph.D.thesis.University of Hong Kong.

Kou,X.Y.;Tan,S.T.;Sze,W.S.(2006):Modeling complex heterogeneous objects with nonmanifold heterogeneous cells.Computer-Aided Design,vol.38,pp.457-474.

Kou,X.Y;Tan,S.T.(2009):Robust and efficient algorithms for rapid prototyping of heterogeneous objects.Rapid Prototyping J.,vol.15,pp.5-18.

König,J.A.(1987):Shakedown of elastic-plastic Structures.PWN-Polish Scienti fi c Publishers.

Lee,Y.D.;Erdogan,F.(1994):Residual/thermal stress in FGM and laminated thermal barrier coating.Int.J.Fracture,vol.69,pp.145-165.

Na,K.S.;Kim,J.H.(2006):Three-dimensional theCompos.Struct.,vol.73,pp.413-422.

Noda,N.;Tsuji,T.(1990):Steady thermal stresses in a plate of functionally gradient material.Proc.1st Int.Symp.Functionally Gradient Materials,pp.339–344.Mark worth,A.J.;Saunders,J.H.(1995):A model of structure optimization for functionally graded materials.Mater.Lett.,vol.22,pp.103–107.

Ootao,Y.;Kawamura,R.;Tanigawa,Y.;Imamura,R.(1999):Optimization of material composition of nonhomogeneous hollow sphere for thermal stress relaxation making use of neural network.Comput.Methods Appl.Mech.Eng,vol.180,pp.185-201.

Parashkevova,L.;Ivanova,J.;Bontcheva,N.(2004):Optimal design of func-tionally graded plates with thermo-elastic-plastic behavior.Comptes Rendus Mecaniquvol.332,pp.493-498.

Peng,X.;Fan,J.;Zeng,X.(1996):Analysis for plastic buckling of thin-walled cylinders via non-classical constitutive theory of plasticity.In.J.Solids and Struct.,vol.33,pp.4495-4509.

Peng,X.;Hu,N.;Zheng,H.;Fang,C.(2009a):Analysis of shakedown of FG Bree plate subjected to coupled thermal-mechanical loadings.Acta Mech.Solida Sinica,vol.22,pp.95-108.

Peng,X.;Ponter,A.R.S.(1993):Extremal properties of Endochronic plasticity,Part II:Extremal path of the Endochronic constitutive equation with a yield surface and application.Int.J.Plasticity,vol.9,pp.567-581.

Peng,X.;Zheng,H.;Hu,N.;Fang,C.(2009b):Static and kinematic shakedown analysis of FG plate subjected to constant mechanical load and cyclically varying temperature change.Composite Structures,vol.91,pp.212-221.

Praveen,G.N.;Reddy,J.N.(1998):Nonlinear transient thermoelastic analysis of functionally graded ceramic-metal plates.Int.J.Solids and Struct.,vol.35,pp.4457-4476.

Qiu,J.;Tani,J.;Warkentin,D.J.(1999):Stress analysis of RAINBOW actuators and relief of stress by gradation of material composition.Japan.Soc.Appl.Electromagn.Mech.,vol.7,pp.185192

Reddy,J.N.(2011):Microstructure-dependent couple stress theories of functionally graded beams.J.Mech.Phys.Solids,vol.59,pp.2382-2399.

Shen,Y.(1998):Thermal expansion of metal–ceramic composites: a three-dimensionalanalysisMater.Sci.Eng.A,vol.252,pp.269-275.

Suresh,S.;Mortensen,A.(1998):Fundamentals of functionally graded materials:processing and thermomechanical behaviour of graded metals and metal-ceramic composites.IOM Communications Ltd,London.

Suresh,S.;Mortensen,A.(1998):Fundamentals of functionally graded materials.London,UK:Institute of Materials.

Tani,J.;Qiu,J.;Morit,A.T.(2001):Functionally gradient piezoelectric actuatorsTrans.Mater.Res.Soc.Japan,vol.26,pp.283286

Vel,S.S.;Batra,R.C.(2002):Exact solution for thermoelastic deformations of functionally graded thick rectangular plates.AIAA J.,vol.40,pp.1421-1433.

Vel,S.S.;Batra,R.C.(2003):Three-dimensional analysis of transient thermal stresses in functionally graded plates.Int.J.Solids.Struct.,vol.40,pp.7181-7196.

Wadley,H.N.G.;Fleck,N.A.;Evans,A.G.(2003):Fabrication and structural performance of periodic cellular metal sandwich structures.Compos.Sci.Technol.,vol.63,pp.2331-2343.

Wang,B.L.;Han,J.C.;Du,S.Y.(2000):Crack problems for functionally graded materials under transient thermal loading.J.Thermal Stresses,vol.23,pp.143-168.

Watari,F.;Yokoyama,A.;Omori,M.;Hirai,T.;Kondo,H.;Uo,M.;Kawasaki,T.(2004):Biocompatibility of materials and development to functionally graded implant for biomedical application.Compos.Sci.Technol.,vol.64,pp.893-908.

Williams,C.B.;Mistree,F.;Rosen,D.W.(2005):Investigation of additive manufacturing processes for the manufacture of parts with designed mesostructure.In:Proc.ASME 2005 design engineering technical conferences,pp.353-364.

Wu,C.P.;Huang,S.E.(2009):Three-Dimensional Solutions of Functionally Graded Piezo-Thermo-Elastic Shells and Plates Using a Modi fi ed Pagano Method.CMC:Computers,Materials,&Continua,vol.12,pp.251-282.

Zheng,H.;Peng,X.;Hu,N.(2012):Analysis for Shakedown of Functionally Graded Plate Subjected to Thermal-Mechanical Loading with Piecewise-ExponentialDistribution of Material Properties.CMES:Comp.Model.Eng.Sci.,vol.86,pp.505-531.

Zhong,Z.;Shang,E.T.(2003):Three-dimensional exact analysis of simply supported functionally gradient piezoelectric plates.Int.J.Solids Struct.,vol.40,pp.5335-5352.