On the Homogenization Analysis of Electromagnetic Properties for Irregular Honeycombs

Lianhua Maand Qingsheng Yang

1 Introduction

As a kind of lightweight materials,honeycombs have a wide range of applications in aircraft and aerospace structures which require structural and electromagnetic characteristics.For instance,due to good dielectric characteristics in the microwave range,honeycombs are suitable for transmitting and receiving aerials,radioparent covers and other microwave applications[Bettermann and Wentzel(1993);Smith(1999);Smith,Scarpa and Chambers(2000)].For these applications and others,the effective macroscopic electromagnetic properties of the heterogeneous material are often needed.There are several approaches to determine the effective properties in electromagnetism.For example,Hashin and Shtrikman(1962)derived bounds for the effective magnetic permeability of multiphase materials using a variational approach,but the anisotropy of effective electromagnetic properties of composites was not considered.Robinson(1973)demonstrated the difficulties involved in the derivation of the macroscopic Maxwell equations from the involving microscopic fundamental fields.Pendry(1996)developed a method for the calculation of effective material properties using line and surface integrals of field quantities.Smith,Scarpa and Chambers(2000)investigated the electromagnetic dielectric properties of honeycombs with a finite difference time domain technique and measured those with a rectangular wave-guide technique on cast epoxy resin samples manufactures with a stereolythography technique.Although several widely-used micromechanical models including the effective medium theory[Bottcher(1952)],the Mori-Tanaka method[Mori and Tanaka(1973)],the self-consistent method[Hill(1965)]can be extended to predict effective electromagnetic properties of composites in some occasions,they can only accurately model heterogeneous materials with simple geometries and low volume fractions of inclusions.For the heterogeneous composites with periodic microstructures,the finite element method(FEM)-based asymptotic homogenization model is a popular numerical approach to compute the overall properties[Bensoussan,Lions and Papanicolau(1978)].Based on the homogenization method,Perin(2004)numerically investigated the relationships between effective electromagnetic properties and volume fraction of inclusions for periodic electromagnetic medium,and upper and lower bounds were determined for its effective electromagnetic constants.Ouchetto,Zouhdi,Bossavit,Griso,Miara and Razek(2007)computed the quasi-static effective electromagnetic parameters of periodic materials and metamaterials.It should be noted that,in addition to the primal FEM,several new numerical models were developed to improve the computational efficiency of the homogenization.For example,Ghosh and Mallett(1994)proposed the idea of Voronoi Cell Finite elements(VCFEMs)to reduce the burden of computation and meshing.Dong and Atluri(2012a,2012b,2013)developed an efficient and highly accurate tool-Treffz Computational Grains(TCGs)for micromechanical modeling of heterogeneous materials.More recently,Bishay,Dong and Atluri(2014)presented Multi-Physics Computational Grains(MPCGs)for modeling porous and composite piezoelectric materials.

This paper is focused on development of a homogenization approach and investigation on effective electromagnetic properties of irregular honeycombs governed by the geometry of the unit cell.The paper is organized as follows:the two-scale asymptotic homogenization theory is developed in Sec.2 to determine effective electromagnetic properties of periodic honeycombs in micro and macro length s-cales.Expressions for the effective conductivity,dielectric permittivity and magnetic permeability tensors,and microscopic and macroscopic governing equations are both derived.For better comparisons,approximate evaluations of effective electromagnetic properties based on the Smith-Scarpa’s semi-empirical formulations are recalled in Sec.3.The detailed information about the finite element analysis of the unit cell is delivered in Sec.4.Effects of different geometric parameters of unit cell on effective permittivities of irregular honeycombs are investigated and discussed in Sec.5.For verifications on the proposed finite element analysis,numerical results are compared with those by using Smith-Scarpa’s semi-empirical formulations Sect.6 summarizes the inclusions of this study.

2 Two-scale asymptotic homogenization theory and its application on the honeycomb

The two-scale asymptotic homogenization method was developed in the later 1970s and early 1980s by applied mathematicians for various heterogeneous materials[Bensoussan,Lions and Papanicolau(1978)]and it has been successfully applied to accurately simulate the effective properties of periodic composite and porous materials[Peng and Cao(2002);Yang and Becker(2004);Kalamkarov,Hassan,Georgiades and Savi(2009);Ma,Rolfe,Yang and Yang(2011);Ma,Yang,Yan and Qin(2014)].The homogenization method assumes that all physical quantities vary in local and global scales and the quantities are periodic with respect to the local scale because of the periodicity of the microstructure.As the periodic dimension approaches zero,the homogenized effective properties can be obtained by FEM

A typical sketch of the honeycomb under investigation is depicted in Fig.1.The normalized geometry of a unit cell is defined by α,β andθ,whereα=h/l,β =t/l,l,h,tand θ are respectively the length,height,thickness and internal cell angle between facets or walls.The unit cell of a conventional honeycomb(α =1,θ =30°)is constructed from six walls(or facets)of equal length arranged such that all the internal angles are equal,and the electromagnetic properties are invariant along the unit cell’s axis geometry.This fact does not give enough freedom to electromagnetic designers for the material selection.However,the effective electromagnetic properties of honeycombs become anisotropic in case the geometry parameters(h/l,t/l,θ,as shown in Fig.1)undergo a change.The unit cell of a honeycomb with different geometries forms an irregular hexagon,which can offer a much greater control on electromagnetic properties by designing geometries of honeycomb cells.For example,auxetic honeycombs can offer superior electromagnetic properties compared to conventional ones[Smith,Scarpa and Chambers(2000)].

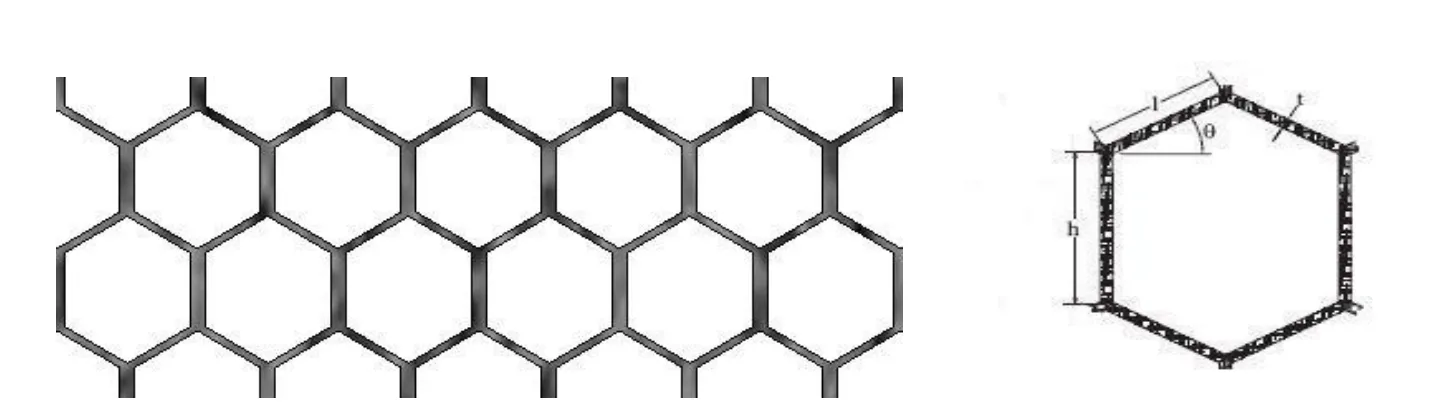
Figure 1:Sketch of honeycomb structure and the geometry of a typical honeycomb unit cell.

Figure 2:Periodically structural honeycomb structure and associated unit cell.

For the periodic honeycombs as shown in Fig.1,microscopic structures in small length scale make the homogenization method become an effective tool for deriving macroscopic electromagnetic properties.This section is devoted to the derivation of the effective electromagnetic coefficients for honeycombs,including dielectric permittivity,magnetic permeability and electrical conductivity tensors,by using the two-scale asymptotic expansion method in the context of homogenization theory.The structures of periodic honeycombs and its periodical microstructure–unit cell,also well-known as the Representative Volume Element(RVE)are illustrated in Fig.2.The unit cell in the small length scale is regarded as a heterogeneous medium made of honeycomb facets and central cavity occupied by air.According to the Maxwell’s equations in steady state,the electric fi ledE,the electric potential φ,the electric flux densityD,the magnetic fieldH,the magnetic potential ϕ,the magnetic flux densityB,the volume density of charge ρ and the electric currentJsatisfy the following equations in each phase of the unit cell:

where ε,µ and σ denote the relative dielectric permittivity,magnetic permeability and electrical conductivity,respectively.

It can be found that Eqs.(1a)-(1c)are all of the same structure mathematically.The left-hand side gives a response to a disturbance and the proportionality constant(ε,µ and σ)is a tensor of rank two.For a system of cubic symmetry,the tensor reduces to a single constant.Suppose that we have numerically solved the problem of determining the homogenized relative dielectric permittivity ε of the honeycomb in terms of the permittivities of the constituent phases and their geometrical distribution.It means the same mathematical expression can then be used to find the homogenized magnetic permeability µ and electrical conductivity σ,if we knowµand σ of the pure phases.It therefore suf fi ces to consider one of the effective electromagnetic properties in Eqs.(1a)-(1c).We start with Eq.(1a)to show how to derive the effective dielectric permittivity ε according to the homogenization theory.

The medium is characterized by two characteristic lengths:a macroscopic oneL,that is the characteristic size of the honeycomb sample;and a microscopic onel,of the order of the characteristic length of the unit cell,as illustrated in Fig.2.A length ratio η=l/Lis thus defined and is assumed to be small.

Now we introduce two distinct length scales,i.e.,the macroscopic scale x and the microscopic one y with a relation y=x/η.Referring to Fig.2,a high level of heterogeneity in the microstructure causes a rapid variation of evolutionary variables,e.g.,electric field and electric flux density in a small neighborhood of the macroscopic scale x with a Y-periodicity.This corresponds to a microscopic scale y and consequently,all variables are assumed to exhibit dependence on the small parameter η,i.e.

Using the differentiation rule such that

According to the homogenization method,the electric potential can be expressed as an asymptotic expansion with respect to parameter η,i.e.

where φ0and φ1are periodic with respect to variabley.Applying the differentiation rule Eq.(4)to the partial differentials of Eq.(2)and Eq(1a)yields,

where

Substituting Eq.(6)into Eq.(1a),the electric flux density is given by:

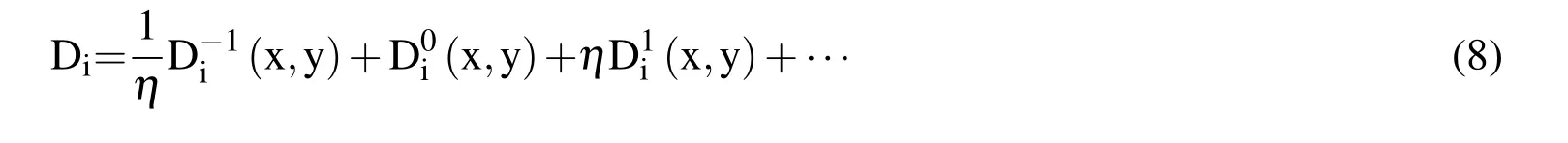
where

Substituting Eq.(8)into Eq.(1a),and equating the power of η,we have

The variational form for Eq.(10a)is

For a Y-periodic function Ψ(y),we de fine a mean operator as follows:

where|Y|is the volume of the unit cell.

When η → 0,applying Eq.(12)to Eq.(11),we have

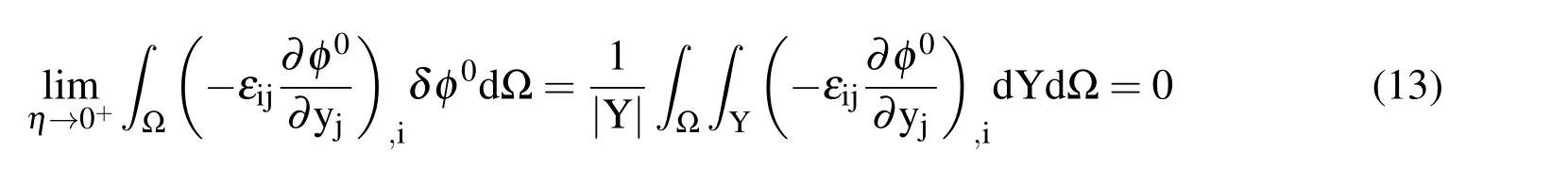
Using the divergence theorem on Eq.(13),we obtain:

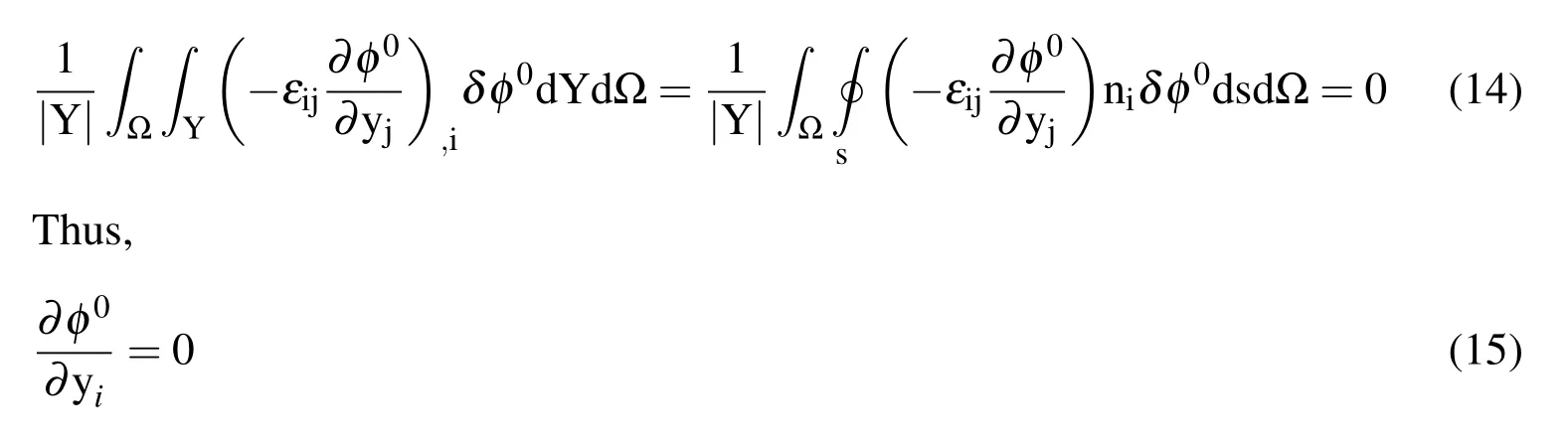
Note that φ0depends on x only,and it can be regarded as the macroscopic electric potential,while φ1,φ2,···are the microscopic electric potentials,which represent the perturbing electric potentials at the micro scale.

From Eq.(7b)and(9),we have

Substituting Eq.(16)into the variational form of Eq.(10b)yields:

Integrating by parts,and nothing that δ φ1=0 at the boundary ofY,and φ0is a function ofxonly,we obtain:

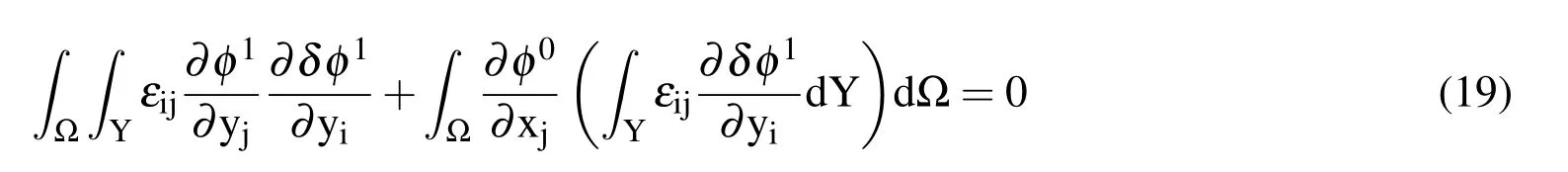
Defining a function χ which satisfies

Introducing Eq.(20)into(19)yields

Applying the divergence theorem leads to

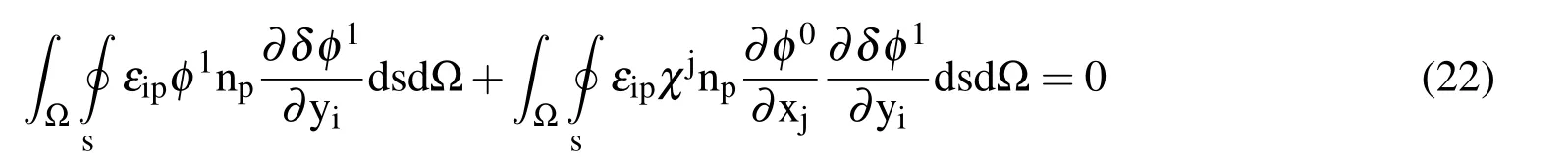
Hence we can obtain

Substituting Eq.(22)into Eq.(16)yields:

For the homogenized electromagnetic body,the constitutive relations can be expressed as

where εiHjdenotes the homogenized dielectric permittivity and χjis the periodic characteristic function with respect to y coordinate system,which needs to be determined through a numerical scheme,such as a finite element procedure.

Hence,electric potential characteristic function χjcan be completely determined from governing equation(20),with specific boundary conditions and initial macroscopic electric potential gradients.Once the characteristic function χjis solved,we can compute the effective permittivity tensor by Eq.(25).

Due to the similarity of equation(1),the process of deriving homogenized effective permeability and conductivity tensors are analogous to those of effective permittivity tensors presented above.Only the fi nal formulations of homogenized effective permeability and conductivity tensors are given as follows,

where ξj,ζjare corresponding characteristic functions which have the periodicity with respect to y coordinate system.

3 Approximations of effective electromagnetic properties for irregular honeycombs

For the effective dielectric permittivity εeof honeycombs,in particular,the Hashin-Shtrikman upper bound[Hashin and Shtrikman(1962)]on the effective permittivity is given by

where εsis the relative dielectric permittivity of solid facet,and υ denotes the volume fraction of solid facet.Eq.(29)implies that the cellular solid is statistically isotropic in the space and it cannot capture the anisotropic properties.In reality,an irregular honeycomb is basically anisotropic.Smith,Scarpa and Burriesci(2002)formulated a semi-empirical formulation of in-plane permittivities based on the Hashin-Shtrikman upper bound and the FD-TD homogenization in a nonlinear least square sense,which can be used to make an initial prediction on the in-plane permittivity for an irregular-shaped honeycomb:

The coefficient L12is a measure of the anisotropy of the honeycomb,and it is given by the ratio of the in-plane Young’s modulus E1and E2,which can be expressed by

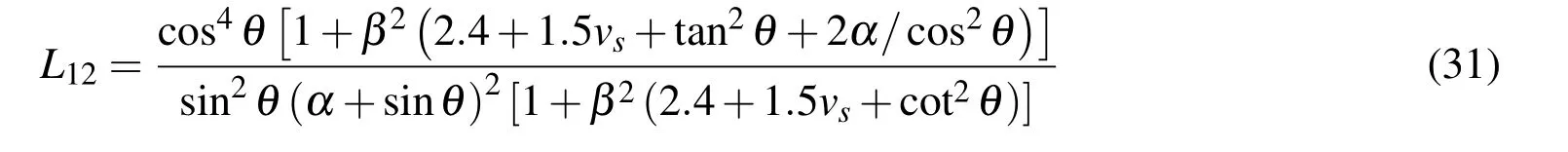
Note that for a hexagonal honeycomb(α =1,θ =30°),the coefficient is close to 1 and in this situation,Eq.(31)degenerates for the case of in-plane isotropic permittivity.

For the commercial double-thickness honeycombs,based on Voigtestimate[Nemat-Nasser and Hori(1993)],the out-of-plane permittivity can be easily given by

where εcis the relative dielectric permittivity of cavity,and the volume fraction of solid facet υ can be written as,

4 Finite element model of the unit cell and its boundary conditions

As discussed above,the characteristic function χjin Eq.(25)can be obtained by FEM together with the periodic boundary conditions of φ1.Fig.3 depicts a series of structures and associated FE meshes of 3D unit cell by selecting different geometry parameters.

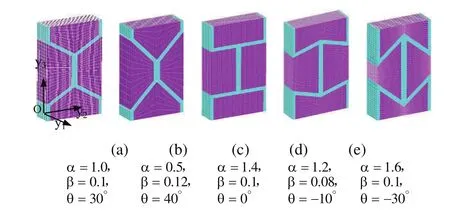
Figure 3:Geometric structures and associated FE models of unit cell.

For the 3D unit cell of honeycombs,y1,y2and y3are the Cartesian coordinates corresponding to axes parallel to the RVE edges and origin at one corner of the RVE,as shown in Fig.3(a).According to the homogenization method,we have the following boundary conditions of unit cell

wherea1,a2anda3are the edge lengths of RVE along y1,y2and y3directions,respectively.

With the application of the proposed solution approach and boundary conditions,we can perform finite element analysis to compute the effective electromagnetic properties of honeycombs.The boundary conditions in Eq.(34)were implemented as constraint equations After the characteristic function χjwas numerically solved by FEM,the homogenized electromagnetic properties of irregular honeycombs could be further calculated in the wide range of volume fractions

5 Effective dielectric permittivities of irregular honeycombs

As one aspect of effective electromagnetic properties,the homogenized dielectric permittiveities of irregular honeycombs were calculated by the homogenization model in the wide range of geometric parameters of unit cell.In this example,the relative dielectric permittivities of the solid facet(glass fiber reinforced epoxy resin)and the cavity in the honeycombs are 4.0 and 1.0,respectively,i.e.εs=4.0,εc=1.0

5.1 Effects of geometric structures of honeycombs on in-plane effective permittivities

Based on the results of asymptotic homogenization,the finite element analysis provides all the local fields needed and then the effective properties are determined.Figs.4(a)-(e)show the contours of local lateral electric flux density D11several typical unit cells subject to initial lateral unit electric field under specifically periodic boundary conditions.

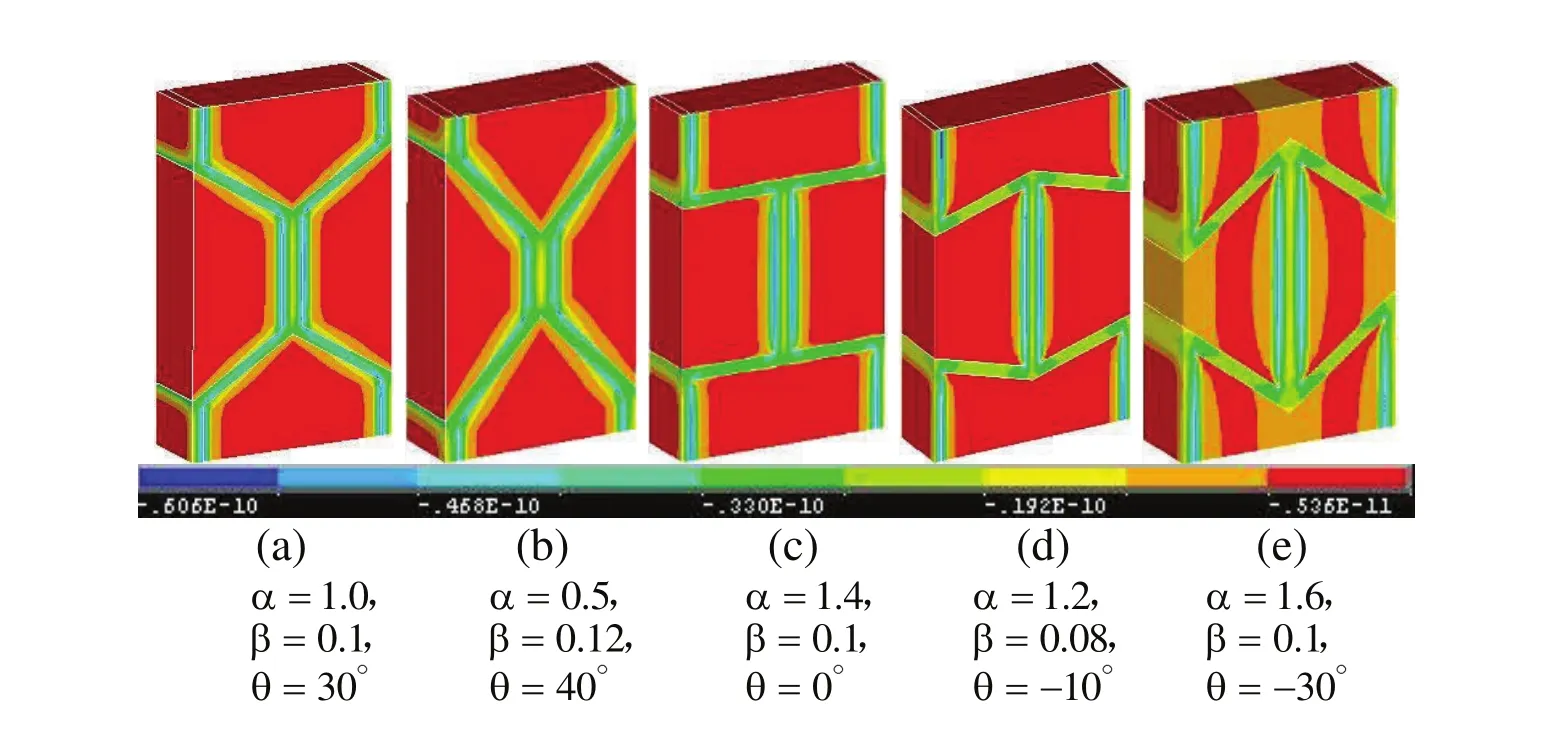
Figure 4:Contours of lateral electric flux density D11of several designed unit cells under initial unit electric field.

As seen from Fig.4,the distribution of electric flux density is not uniform due to the heterogeneous microstructure of honeycomb material.It is noted that the other local field variables including electric flux densities D22,D33and electric fields E11,E22,E33can be similarly determined by this two-scale homogenization method.It is easy to understand the homogenized field variable is dependent on the designed structure of honeycomb unit cell.Based on the numerical results of different field variables,we can calculate the corresponding effective electromagnetic tensors by Eqs(25)and(28).

Using the present two-scale homogenization method,Smith-Scarpa’ssemi-empirical formulation Eq(30)and Eq(32),the effective dielectric permittivities εex/εs,εey/εsand εez/εsare calculated by varying geometric parameters.Figs 5 and 6 show the numerical and semi-empirical results related in-plane effective relative permittivities when the geometric parameters of the unit cell are varied.

It is found that the effective in-plane permittivities critically depend on geometric parameters α,β and θ in a general honeycomb.The effective in-plane permittivities obtained from the two-scale homogenization method are lower than those Smith-Scarpa’s semi-empirical solutions when the honeycombs are nearly reentrant(θ ＜ 0).When increasing the value of θ,the calculated permittivities by the present model are higher than the semi-empirical results.Also in these four groups of results,larger discrepancies between homogenization results and semi-empirical solutions are clearly visible at some points.However,the trends of the variations of both two in-plane effective dielectric permittivities are still similar with varying geometries of honeycombs,which are all going from up to down.Comparatively,the parameter α(see Figs.5a,6a)shows a bit different manner on in-plane permittivities compared to β (see Figs.5b,6b).If the parameter β is fixed,the increases of cell angle θ always lead to a convergence of εex/εs(εey/εs)when θ increases to a certain extent.In this case,the honeycomb configurations show less sensitivity versus the effective permittivities,with the increases of θ and α .On the other hand,when the parameter α is fixed,the effective in-plane permittivities εex/εsand εey/εshave the similar situations relying on the variations of β and θ (see Figs.5b,6b).Whatever the variations of θ ,the increasing geometric parameters β can definitely strengthen the overall dielectric properties.As mentioned above,apparent discrepancies between homogenization-based results and semi-empirical solutions are observed for high internal cell angles θ,both in the positive and negative angle ranges.In fact,we found that the Smith-Scarpa’s approximate formulation was actually conducted by least-square fitting with a limited number of sampling data and thus it was naturally less rigorous than the present method in a homogenization sense.In the light of this,we suggest the Smith-Scarpa’s approximate formulation cannot be directly used for a wide range of applications,especially on the prediction of in-plane anisotropic properties for irregular honeycombs.Since the homogenization method has a rigorous mathematical background,it is particularly useful for microstructures with complex and irregular configurations.Because of these features,the results of effective permittivities of honeycombs from asymptotic homogenization are more reliable,compared to Smith-Scarpa’s semi-empirical results.

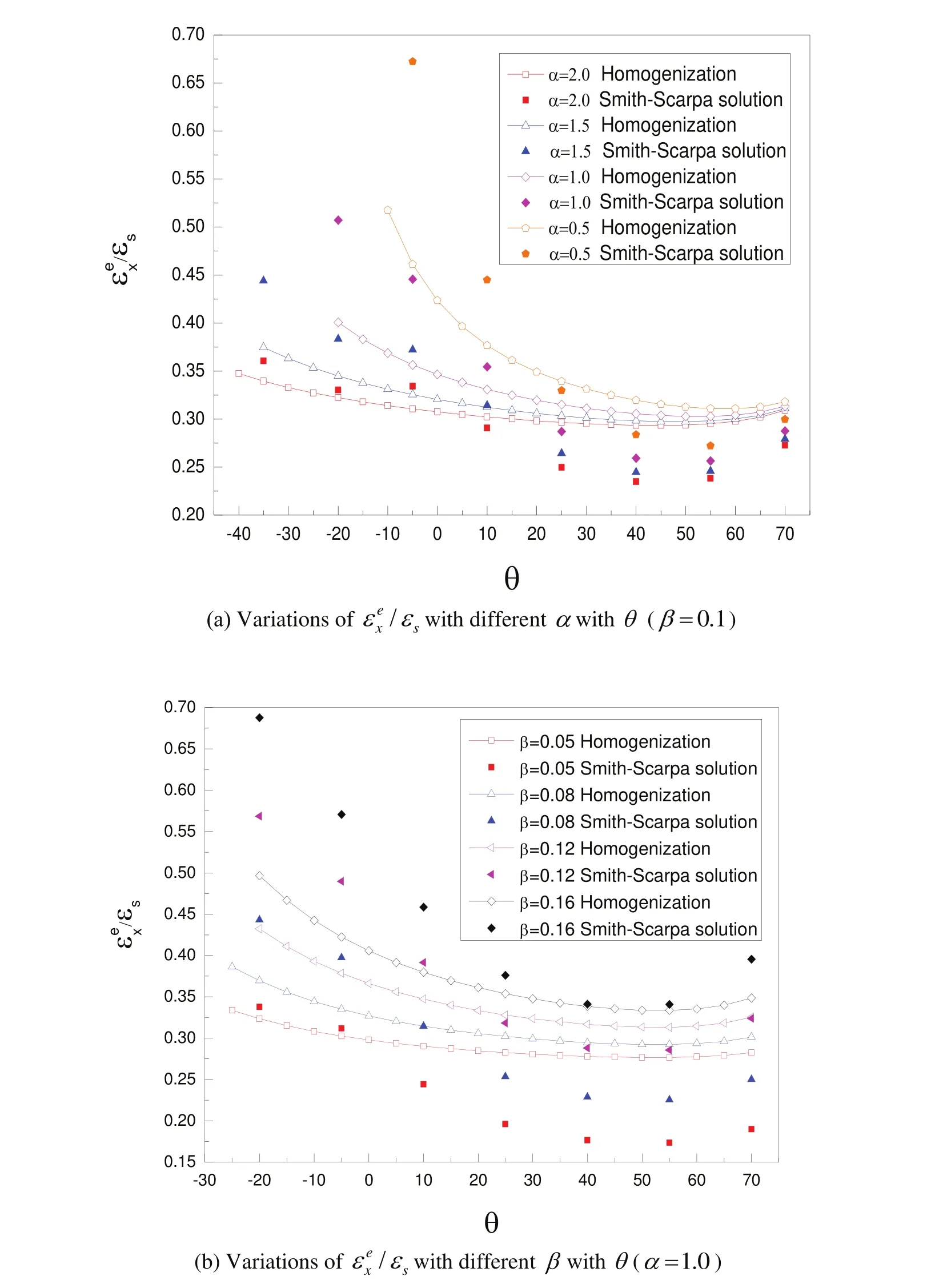
Figure 5:Relations between effective permittivity εex/εsand geometric parameters.

Figure 6:Relations between effective permittivity εey/εsand geometric parameters.

Figure 7:Relations between effective permittivity εez/εsand geometric parameters.

5.2 Effects of geometric structures of honeycombs on out-of-plane effective permittivities

With the use of two-scale homogenization method and Eq(32),the out-of-plane effective dielectric permittivities εez/εswere plotted against geometric parameters of unit cell in Fig 7.

In comparison with εey/εs,the out-of-plane effective permittivity εez/εshas the similar variation manner depending on unit cell geometry.The increases of θ also provides a convergence of εez/εswhen θ increases to 70°.From Fig.7(a),the effective permittivity εez/εsof auxetic honeycomb(θ ＜ 0°)is sensitively dependent on geometric parameters,which can give enough space to structural and electromagnetic design engineer for honeycomb material selection.We can also find from Fig.7,that predictions of out-of-plane effective permittivities εez/εsform Eq.(32),are in substantial agreement with homogenization-based results,and the estimations from Eq.(32)are higher than the numerical results,especially in the case of large magnitudes of θ and β which lead to large volume fraction of solid facet.Despite Eq.(32)overestimates the out-of-plane effective permittivity εze/εs,it is more acceptable than Smith-Scarpa’s semi-empirical equations Eq.(30)used for the estimations of in-plane effective permittivities εxe/εs,εye/εs.

For the general honeycombs investigated in this study,the convenient choice of geometric parameters of unit cell facilitates appropriate effective electromagnetic properties expected and it also provides more flexibility on optimization design of honeycomb components with the applications of irregular cells.Compared to semi-empirical estimations,the proposed two-scale homogenization method offers a useful tool to compute accurately the effective dielectric properties of irregular honeycombs.

It can be observed from Eq.(28)that expressions of the electrical conductivity and magnetic permeability coefficients are analogous to that of dielectric permittivity.Despite the fact effective dielectric permittivity was only investigated,the other two electromagnetic parameters,effective magnetic permeability and electrical conductivity can be determined by the same approach.For reasons of mathematical analogy,the effects of the unit cell geometry on dielectric properties of honeycomb material are also valid for effective magnetic permeability and electrical conductivity of such ferromagnetic and conductive materials.

6 Conclusions

Electromagnetic honeycombs were analyzed by using a two-scale homogenization model and finite element analysis from the electromagnetic point of view.The expressions of effective electromagnetic coefficients are deduced from the two-scale homogenization theory.A solution method based on a unit cell approach was developed to calculate accurately effective electromagnetic properties.In examples,numerical results of homogenized permittivities were compared with the previous semi-empirical solutions,and it proved that the proposed homogenization method and numerical modeling is valid and efficient.Whatever the geometry of honeycomb materials,the two-scale homogenization method gives the variations of the electric and magnetic fields at the level of the microstructure,and furnishes a rigorous deductive procedure for deriving effective electromagnetic tensors and macro-micro governing equations,while the semi-empirical formulations fail to accurately predict the effective permittivity,especially for the in-plane properties of anisotropic honeycombs with distinct variations of geometric structures.Further by using the present method,the effect of geometry of honeycomb’s unit cell on effective permittivity was investigated,which shows that the effective electromagnetic properties are dramatically dependent on the geometric characterization of such honeycomb composites.

In summary,our calculations con fi rm that the two-scale homogenization approach leads to accurate effective electromagnetic constants of honeycombs.Moreover,this method can be easily applied to determine the effective electromagnetic properties for other periodic composite materials and structures.

Acknowledgement:The financial supports from the Natural Science Foundation of China under grant#11172012and National Key Technology R&D Program under grant#2012BAK29B00 are gratefully acknowledged.

Bensoussan,A.;Lions,J.L.;Papanicolau,G.(1978):Asymptotic analysis for periodic structures.North Holland,Amsterdam.

Bettermann,J.;Wentzel,H.(1993):Design features and test of low observable structures for large aircraft.Proc.3rd Int.Conf.Electromagnetics in Aerospace Applications,Politec.Torino,pp.14–17.

Bishay,P.L.;Dong,L.;Atluri,S.N.(2014):Multi-physics computational grains(MPCGs)for direct numerical simulation(DNS)of piezoelectric composite/porous materials and structures.Computational Mechanics,DOI:10.1007/s00466-014-1044-y.

Bottcher,C.J.E.(1952):Theory of Electric Polarization,Elsevier,Amsterdam.

Dong,L.;Atluri,S.N.(2012a):T-Trefftz Voronoi Cell Finite Elements with elastic/rigid inclusions or voids for micromechanical analysis of composite and porous materials.CMES:Computer Modeling in Engineering&Sciences,vol.83,no.2,pp.183–219.

Dong,L.;Atluri,S.N.(2012b):Development of 3D Trefftz Voronoi Cells with ellipsoidal voids&/or elastic/rigid inclusions for micromechanical modeling of heterogeneous Materials.CMC:Computers,Materials&Continua,vol.30,no.1,pp.39–81.

Dong,L.;Atluri,S.N.(2013):SGBEM Voronoi Cells(SVCs),with embedded arbitrary-shaped inclusions,voids,and/or cracks,for micromechanical modeling of heterogeneous materials.CMC:Computers,Materials&Continua,vol.33,no.2,pp.111–154.

Ghosh,S.;Mallett,R.L.(1994):Voronoi cell finite elements.Computers&Structures,vol.50,no.1,pp.33–46.

Hashin,Z.;Shtrikman,S.(1962):A variational approach to the theory of the effective magnetic permeability of multiphase materials.Journal of Applied Physics,vol.33,pp.3125–3131.

Hill,R.(1965):A self-consistent mechanics of composite materials.Journal of the Mechanics and Physics of Solids,vol.13,pp.213–222.

Kalamkarov,A.L.;Hassan,E.M.;Georgiades,A.V.;Savi,M.A.(2009):Asymptotic homogenization model for 3D grid-reinforced composite structures with generally orthotropic reinforcements.Composite Structures,vol.89,pp.186–196.

Ma,L.H.;Rolfe,B.F.;Yang,Q.S.;Yang,C.H.(2011):The configuration evolution and macroscopic elasticity of fluid- filled closed cell composites:micromechanics and multiscale homogenization modeling.CMES-Computer Modeling in Engineering&Sciences,vol.79,no.2,pp.131–158.

Ma,L.H.;Yang,Q.S.;Yan,X.H.;Qin,Q.H.(2014):Elastoplastic mechanics of porous materials with varied inner pressures.Mechanics of Materials,vol.73,pp.58–75.

Mori,T.;Tanaka,K.(1973):Average stress in matrix and average elastic energy of materials with mis fitting inclusions.Acta Metallurgica,vol.21,pp.571–574.

Nemat-Nasser,S.;Hori,M.(1993):Micromechanics:Overall properties of heterogeneous materials,Elsevier,Amsterdam.

Ouchetto,O.;Zouhdi,S.;Bossavit,A.;Griso,G.;Miara,B.;Razek,A.(2007):Homogenization of structured electromagnetic materials and metamaterials.Journal of Materials Processing Technology,vol.181,pp 225–229.

Pendry,J.B.(1996):Calculating photonic band structure.Journal of Physics:Condensed Matter,vol.8,pp.1085–1108.

Peng,X.Q.;Cao,J.(2002):A dual homogenization and finite element approach for material characterization of textile composites.Composites:Part B,vol.33,no.1,pp.45–56.

Perin,F.(2004):Bounds and asymptotic results for the effective electromagnetic properties of a locally periodic distribution of conducting inclusions in a conducting matrix.European Journal of Mechanics A/Solids,vol.23,pp.139–157.

Robinson,F.N.H.(1973):Macroscopic Electromagnetism,Pergamon Press,Oxford,UK.

Smith,F.C.(1999):Effective permittivity of dielectric honeycombs.Proc.Inst.Elect.Eng.,Microw.,Antennas,Propagat.,vol.146,no.1,pp.55–59

Smith,F.C.;Scarpa,F.;Burriesci,G.(2002):Simultaneous optimization of the electromagnetic and mechanical properties of honeycomb materials.Proc.SPIE.vol.4701,pp.582–590.

Smith,F.C.;Scarpa,F.;Chambers,B.(2000):The electromagnetic properties of re-entrant dielectric honeycombs.IEEE Microwave and Guided Wave Letters,vol.10,pp.451–453.

Yang,Q.S.;Becker,W.(2004):Numerical investigation for stress,strain and energy homogenization of orthotropic composite with periodic microstructure and non-symmetric inclusions.Computational Materials Science,vol.31,pp.169–180.