浅析动力学问题的求解方法
2014-04-17赵丽霞
赵丽霞
(安徽理工大学理学院力学系,安徽 淮南 232001)
动力学是研究物体运动与力之间关系的学科,生活日益发展的今天,动力学已经涉及到各个领域,生产方面:石油的开采、汽车的研发、航空航海、机械的研发等。生活方面:足球动力学、排球动力学、高尔夫动力学等。因此,随着动力学的广泛应用,研究该问题的求解方法不仅有着重要的理论意义,而且具有重要的工程实践意义。在经典力学的发展中,对动力学问题的研究主要有两个角度:牛顿力学和分析力学。
1 牛顿力学
牛顿力学大量运用几何方法和矢量作为研究工具,因此它又被称为矢量力学。其求解动力学问题时主要依据的就是我们比较熟悉的动量定理、动量矩定理、动能定理三大动力学普遍定理。
1.1 主要内容
(1)动量定理
在某一时间间隔内,质点系动量的改变量等于在这段时间内作用于质点系外力冲量的矢量和。即

(2)动量矩定理
质点系对某固定点O的动量矩对时间的导数,等于作用于质点系的外力对于同一点的矩的矢量和。即
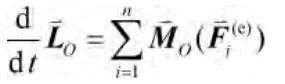
(3)动能定理
质点系在某一运动过程中,起点和终点的动能的改变量,等于作用于质点系的全部力在这一过程中所作的功之和。即
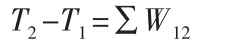
1.2 动力学三大定理的对比分析
(1)动量定理反应力对时间的累积效应,而动能定理反应力对路程的累积效应。
(2)动量和动能定理无需对过程是怎样变化的细节深入的研究,而更关心的是运动状态变化即改变结果量及其引起变化的原因。对任何过程的恒力、变力;匀变速、非匀变速;直线运动、曲线运动;时间长、瞬间过程;单、多过程都能运用。但动量矩定理只适用于瞬时状态。
(3)动量和动量矩定理表达式均是矢量形式,且内力不参与计算;动能定理表达式为标量形式,并且若系统内力做功,方程中也必须包含该内力。
1.3 使用动力学三大定理解题的优先顺序
(1)在涉及力、位移时优先考虑能量途径。
(2)在涉及力、时间时优先考虑动量途径。
(3)若研究对象做定轴转动或平面运动,则一般先考虑动量矩定理。
2 分析力学
分析力学是理论力学的一个分支,它通过用广义坐标为描述质点系的变数,运用数学分析的方法,研究宏观现象中的力学问题,是对经典力学的高度数学化的表达。分析力学是独立于牛顿力学的描述力学世界的体系。分析力学的基本原理同牛顿运动三定律之间可以互相推出。分析力学又分为拉格朗日力学或哈密顿力学。前者以拉格朗日量刻划力学系统,运动方程称为拉格朗日方程,后者以哈密顿量刻划力学系统,运动方程为哈密顿正则方程。
2.1 主要内容
(1)动力学普遍方程
在理想约束情况下,任一瞬时,作用于质点系上的主动力和惯性力在质点系的任意虚位移上所作虚功之和等于零。即
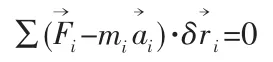
(2)拉格朗日方程
其中T为质点系的动能;L为质点系的动势L=T-V;qk为广义坐标;q·k为广义速度。
(3)哈密顿正则方程
2.2 三种方程的对比分析
(1)在动力学普遍方程中不会出现约束反力,它提供了具有任意多自由度系统的全部运动方程,但是由于约束的存在,求解时需找出虚位移之间的关系,有时很不方便。
(2)拉格朗日方程采用广义坐标建立,它提供了与广义坐标数目相同的一组独立微分方程,对于解决复杂质点系的动力学问题是比较简便和有效的。
(3)哈密顿正则方程与拉格朗日方程是等价的,将广义动量引入到方程中,方程数目比拉格朗日方程数目更多,但是它的形式是简单而对称的,而且微分方程阶数低,更易于求解。
3 牛顿力学与分析力学的对比分析
(1)牛顿力学以牛顿定律为理论基础,分析力学的基本原理主要是虚功原理和达朗伯原理,而前者是分析静力学的基础;前后两者结合,便可得到动力学普遍方程,从而导出分析力学各种系统的动力方程。
(2)牛顿力学主要采用几何法求解问题,而分析力学主要是运用分析的方法。
(3)在研究观点上牛顿力学侧重力,分析力学则是侧重更广泛意义的能量,所以它具有高度的统一性和普遍性。
(4)分析力学引入了广义坐标、广义力、广义动量等,使分析力学的方法与结论所适用的范围可以超出力学的领域。它广泛用于结构分析、机器动力学与振动、航天力学、多刚体系统和机器人动力学以及各种工程技术领域,也可推广应用于连续介质力学和相对论力学。
(5)牛顿力学与分析力学的研究对象都可以是质点系,质点系可视为一切宏观物体组成的力学系统的理想模型。例如刚体、弹性体、流体等以及它们的综合体都可看作质点系,质点数可由1到无穷。但在牛顿力学中的质点系主要是刚体,而分析力学中的质点系可以推广到弹性体、流体等以及它们的综合体。
(6)对于自由质点或比较简单的质点系,牛顿力学与分析力学两种方法无优劣之分,有时后者反而显得麻烦一些,但是分析力学对于具有约束的复杂质点系的求解更为优越,因为有了约束方程,系统的自由度就可减少,运动微分方程组的阶数随之降低,更易于求解。
4 结论
通过前面的分析,我们知道动力学问题的求解方法比较多,在工程实际中,应根据具体问题类型选择最佳的求解方法,这就需要我们熟悉各种求解方法的适用范围及优缺点。同时,通过牛顿力学与分析力学的对比,从对运动方程建立的方法的研究,可以看出分析力学具有更高的统一性和普遍性,它的适用范围可以超出力学领域向其它学科延伸。
[1]王振发.分析力学[M].科学出版社.
[2]郭志荣,王晨,等.理论力学中的牛顿力学与分析力学方法之浅析[J].廊坊师范学院学报,2009(02).
[3]哈尔滨工业大学理论力学教研室.理论力学[M].高等教育出版社.
