独立学院高等数学教学中融入数学实验的实践

李繁荣 LI Fan-rong；崔艳英 CUI Yan-ying

（北京工业大学耿丹学院，北京 101301）

（Gengdan Institute of Beijing University of Technology，Beijing 101301，China）

1 独立学院高等数学教改的思路

独立学院作为“未来我国高等教育发展的有力补充”，增加了民众接受高等教育的机会（大批精英教育时期上不了大学的学生也可以接受高等教育），其确立了应用型而非学术型人才的培养目标。目前，独立学院高等数学课程的教学大多借鉴甚至照搬一本或二本院校的模式。但针对发生了根本改变的学生现状，教育内容和教育方法迫切需要改变。

高等数学是一门抽象的学科，依靠逻辑而不是观测结果作为其真理的标准，但同时也使用观测、模拟的手段作为发现真理的手段[1]。“学习任何东西，最好的途径是自己去发现”（G·波利亚）。在“大众本科教育”的理念下，基于独立学院的人才培养目标，本院采取了应用Matlab，在高等数学中融入数学实验的教学改革。在重点介绍基本概念、基本思想、基本方法的前提下，实现数学软件Matlab与高等数学内容的整合，利用Matlab强大的图形绘制功能，将难以讲解说明的数学规律显现出来，舍去一些繁琐、冗长的数学结论、定理的理论证明，代之以实验的方法去验证，并利用数学软件Matlab的计算功能弱化运算的技能技巧。

2 应用Matlab，在高等数学中融入数学实验的意义

应用Matlab的图形绘制功能，可以使得高等数学教学中过去用很长时间很难理解的问题变得直观、容易，而且亲身经历式的数学实验使得数学的学习不再那么枯燥乏味，不再是被动的吸收而是主动的获取[2]，更好地发挥了数学实验在高等数学学习中的优势，重塑了学生学习数学的信心，有效地激发了学生的学习兴趣；利用数学软件matlab在实验室进行高等数学的教学，让学生借助计算机去探索数学问题，形成一定的数学素养，从而在实践、实习、毕业设计等实践环节中自觉地运用数学，提高了学生应用数学的能力，有助于完成应用型人才的培养目标，提高应用型人才的综合素质。同时也将全面提高教师的教学水平和综合能力。

3 教学实例

多元函数微积分学一直是高等数学课程中重要而又非常难以掌握的部分，学生理解起来总存在很大的闲难，究其原因，主要是空间想象能力有限，在教学时为了加深学生对知识点的深刻认识，可以利用Matlab强大的图形绘制功能，绘制出三维曲面图形，从而能够让同学们直观的认识多元函数，克服心理和知识上的困难。下面以多元函数极值内容为例，简述怎样应用Matlab将数学实验融入高等数学的教学。

实验1：例1、运用Matlab绘制三个二次曲面图形。

①z=x2+y2②z=- x2+y2

得到如图1所示。

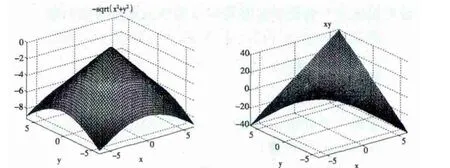
图1

让学生分析三个函数在点P（0，0）的函数值与点P领域内其他点函数值的大小关系，再结合一元函数极值的概念，推广出二元函数极值的概念，老师再给出严谨的定义。

思考题：怎么找出所有的极值点？

一元函数极值点的特征：极值点 驻点或不可导点。

实验2：分析二元函数在极值点的偏导数

在Matlab命令窗口运行

图2

从图2可以看到当y固定在y=0时，函数①z=x2+0=x2和都是以x为自变量，z为应变量的一元函数，图形为两条曲线，二元函数的极值点分别是这两个一元函数的极值点，得到：函数①z=x2+y2在极值点P（0，0）有（0，0）=0，函数在极值点 P（0，0）对x的偏导数不存在，再让学生自己动手分析出：函数①z=x2+y2在极值点 P（0，0）有（0，0）=0，函数在极值点P（0，0）对y的偏导数不存在。再让学生分析函数③z=xy 在点 P（0，0）的偏导数，得到=0。最后归纳总结出类似于一元函数极值的结论：极值点 驻点或偏导数不存在的点，并得到求二元函数极值的步骤如下：

第二步判别所有可疑的极值点是否为极值点。

思考题：对于驻点或偏导数不存在的点怎么判别其是否为极值点？有同学回答可以从图形上直接观察判断。

例2、设z=x4-8xy+2y2-3，求f（x，y）的极值点和极值。

求得三个驻点，分别是 P（-2，-4），Q（0，0），R（2，4）。

在Matlab命令窗口运行

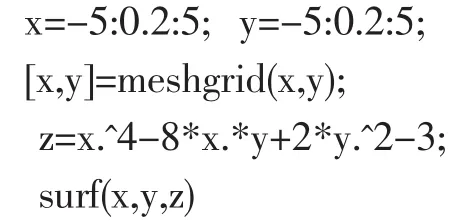
可见在图3中不容易观测极值点，这是因为z的取值范围为[-200，1000]，是一幅远景图，局部信息丢失较多，观测不到图像细节。

实验3、分析例1中三个函数在点（0，0）附近的等高线：①z=x2+y2（图4）

图3

contour(x,y,z,20)%参数20是等高线的数量

③z=xy（图 6）

图4

图5

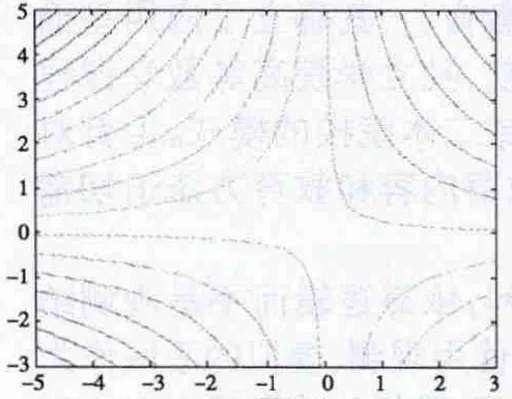
图6

图7

引导学生分析总结出：在两个极值点附近，等高线是封闭的；非极值点附近，等高线不封闭。由此得到从图形上判断可疑的极值点是否为极值点的方法。

让学生动手画出例2中函数的等高线（图7）。

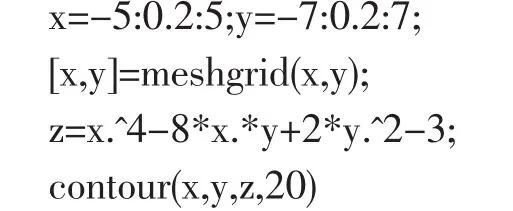
由图 7 可见，点 P（-2，-4）和 R（2，4）有等高线环绕，随着图形灰度的逐渐变浅，函数值逐渐减小，点P（-2，-4）和 R（2，4）均为极小值点，而点 Q（0，0）周围没有等高线环绕，不是极值点。最后再介绍一下极值点的充分条件定理，感兴趣的同学可以课后自学。

通过对以上内容的学习，学生在实验过程中直观、深入地了解了二元函数极值的概念和求二元函数极值的方法，同时提高了学生学习兴趣和动手能力。在高等数学的教学中融入数学实验，运用数学软件matlab深入浅出地将数学中的概念、定理介绍给学生，让学生真正理解并熟练运用它们解决实际问题，是一种有效提高学生学习兴趣和动手能力，反过来促进他们理解数学概念、定理的教学方法。

[1]美国国家研究委员会.人人关心数学教育的未来[M].世界图书发行公司,1993.

[2]毕义明,郝琳.论大学数学实验的内容与实现方法[J].实验室研究与探索,2005,24（7）∶62-64.

[3]姜启源等编著,萧树铁主编.数学实验[M].高等教育出版社,1999.