基于ADAMS的PUMA560的运动学分析及仿真

□ 张永贵 □ 王得蛟 □ 张秀林

兰州理工大学 机电工程学院 兰州 730050

焊接加工一方面要求工人有熟练的操作技能、丰富的实践经验和稳定的焊接水平;另一方面，工作的劳动条件差、烟尘多、热辐射大、危险性高。当焊缝为复杂曲线时，人工焊接质量就会下降，所以，在焊接生产中利用焊接机器人代替人工焊接，可减轻工人的劳动强度，保证焊接质量和提高焊接效率［1］。为保证焊接质量，研制时需对其进行轨迹设计和运动学分析，机械手的运动学模型是其运动规划和离线控制的基础［2,3］。基于上述分析，本文首先以PUMA560机械手为研究对象进行运动学研究分析，然后建立该机械手末端位姿数学模型，进行仿真实验研究，证明模型的准确性。

1 基于PUMA560机械手的运动学分析

1.1 机械手运动学

机械手运动学是避障路径规划研究的基础，主要研究机械手臂各杆件之间的位移、速度和加速度关系，运动学问题包括正运动学问题和逆运动学问题［4］。正运动学问题是指给出机械手各关节的位置、速度、加速度，求解各杆件的位置、姿态、速度、加速度等运动参数的问题，特别是求解机械手手臂端点(或末端杆件)的位置、姿态、速度、加速度［5］。 逆运动学问题是已知工作所要求的末端执行器的位置、姿态、速度、加速度时，求解能实现这些要求的机械手各关节的位置、速度、加速度等运动参数［6］。

1.2 建立机械手末端位姿数学模型

PUMA560机器人本体关节结构由回转的机体、肩、大臂、小臂、腕部及机械手部分组成。

所以该机器人共有6个关节自由度,如图1机器人实体模型所示，其中前3个关节主要影响末端执行器的位置，后3个关节决定末端的姿态，而且6个关节均为旋转关节，属关节型机器人。

▲图1 PUMA560的实体模型

通过机构分析，建立了PUMA560的简化模型，如图2所示，为了进一步分析研究，对已建立的简化模型进行坐标分析研究，如图3所示。同时为了更加有效地实施动力学分析，确定了各参数，见表1。

图中：a2=431.8 mm，a3=20.32 mm，d1=660.4 mm，d2=149.1 mm，d4=433.1 mm，d5=56.25 mm， d6=80.31mm。

1.3 基于已建立模型的运动学分析

1.3.1 正运动学分析

基于D-H方法［7］，表示初始连杆坐标系与上一连杆坐标系之间的关系，相邻两连杆的空间关系矩阵为连杆变换矩阵，建立的齐次变换矩阵如下：

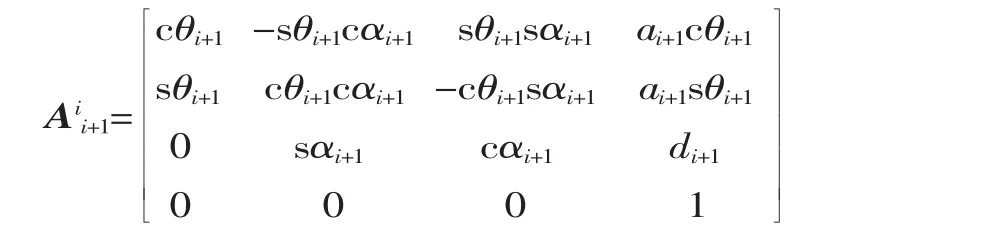
式中：c 为 cos；s为 sin；ai为 Zi-1到 Zi沿 Xi-1测量的距离；αi为 Zi-1到 Zi绕 Xi-1旋转的角度；di为 Xi-1到 Xi沿Zi测量的距离；θi为Xi-1到Xi绕Zi旋转的角度。

▲图2 PUMA560简化模型

▲图3 PUMA560机器人的坐标

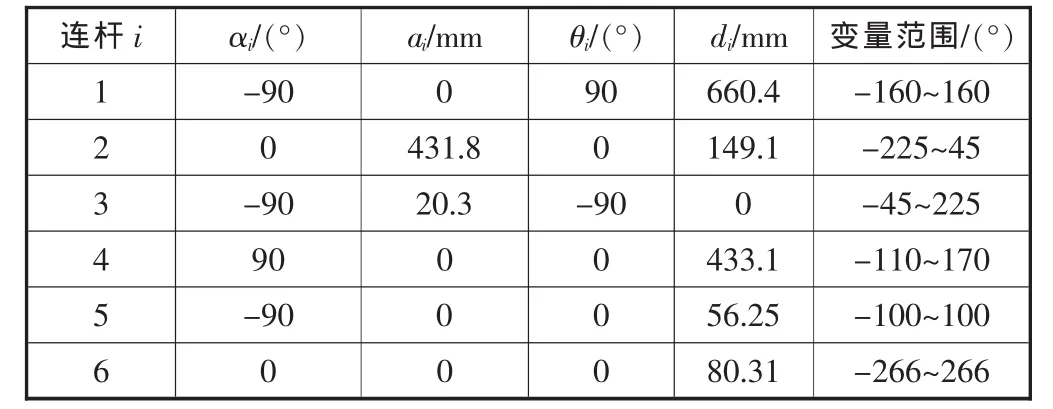
表1 PUMA560机器人的连杆参数

已知6关节机械手运动方程为：

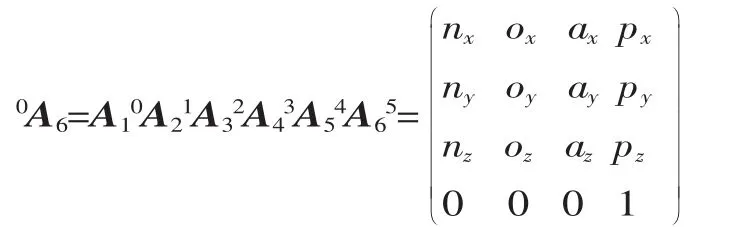
式中：n、o、a 为旋转矢量；p 为平移矢量。

则通过以上的相邻连杆的变换矩阵，得出坐标系6相对于基坐标系0的变换矩阵为：

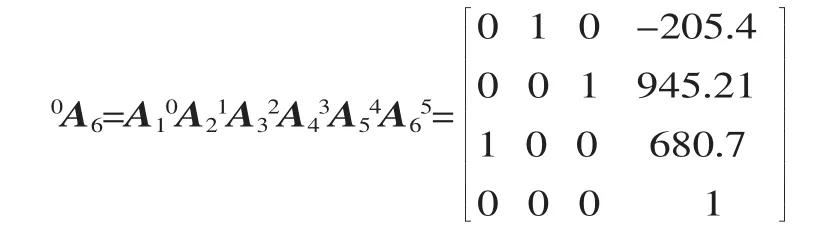
由此可知与图3所示的情况完全一致。

机械手末端相对于基座标的位姿为：

那么机械手末端在ADAMS坐标系中的位姿为：

令肩关节绕Y轴旋转-90°，小臂关节绕X轴旋转90°，其它的关节不旋转，得到机械手末端在ADAMS坐标系中的位姿为：

1.3.2 逆运动学分析

已知机械手末端的位姿0T6，求解各关节变量θi=（i=1，2，3，4，5，6）。 对0A6式两边依次左乘 A 的逆矩阵，并使两端相等矩阵的对应元素相等，可求出各关节变量：

θ1=arctan（px/py）或 θ1=arctan（px/py）+180°令：s234=sin（θ2+θ3+θ4）；c234=cos（θ2+θ3+θ4）；θ234=θ2+θ3+θ4；c1=cosθ1；c3=cosθ3；s1=sinθ1；s3=sinθ3。

则有：

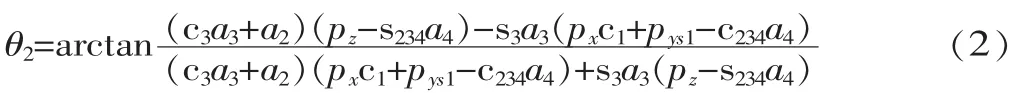
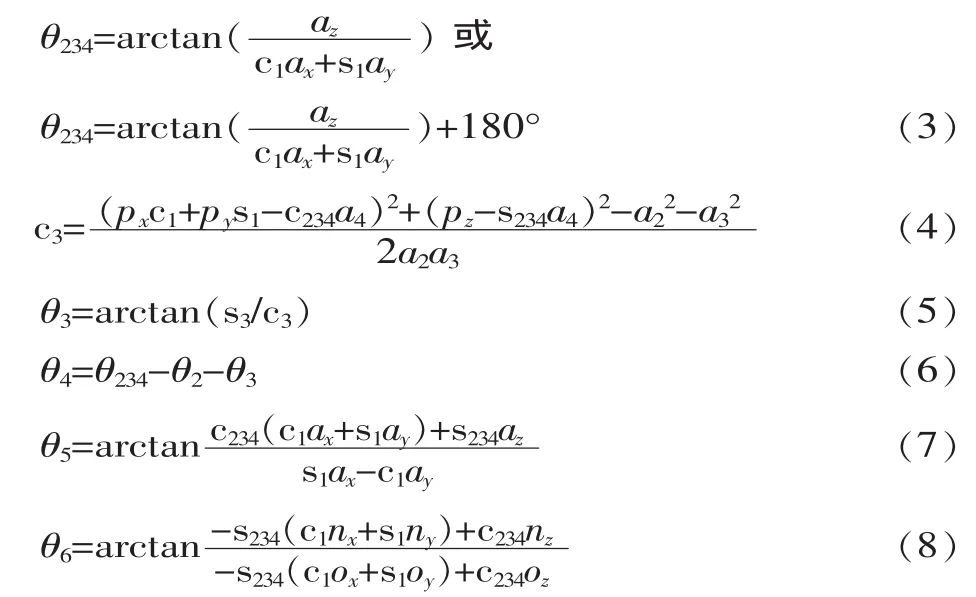
综上分析PUMA560的运动反解可能存在8种解。限于本身结构限制，机械手各关节变量不可能全部在360°范围内运动，所以部分解不能实现，为了满足工作需求，根据一些约束条件选取其中最满意的一组。

2 仿真实验分析

为了验证上述分析的准确性，首先对模型进行仿真实验分析，结果如图4和图5所示，然后采用ADAMS软件处理得到位移曲线如图6所示。

通过上述分析可以看出，机械手末端在0 s时刻的坐标为（102,134，-205.4），与T式的计算结果相近。机械手的末端在3 s时的坐标为(205,210,436)，与T’式的计算结果相近，证明了所建模型的准确性。

3 结论

通过仿真实验分析，证明了本文对PUMA560机械手的研究分析的准确性，以及所建模型的有效性，为进一步研究机械手动力学问题奠定了基础。

▲图4 仿真前各连杆之间位置关系

▲图5 仿真后各连杆之间位置关系

▲图6 末端位移曲线

［1］ 王玉，王旗华.焊接机器人虚拟样机轨迹模拟和运动仿真分析［J］.焊接学报，2012，33（4）.

［2］ 干敏耀，马骏骑.基于MATLAB的PUMA机器人运动学仿真［J］.昆明理工大学学报，2003，28（6）.

［3］ 臧庆凯，李春贵，闫向磊.基于MATLAB的PUMA560机器人运动仿真研究［J］.广西科学院学报，2010，26（4）：397-400.

［4］ 张铁，谢存禧.机器人学［M］.广州：华南理工大学出版社，2004.

［5］ 蔡自兴.机器人学［M］.北京：清华大学出版社，2000.

［6］ 蒋新松.机器人学导论［M ］.沈阳：辽宁科学技术出版社，1994.

［7］ 马香峰.机器人结构学［M］.北京：机械工业出版社，1991.

［8］ 李增刚.ADAMS入门详解与实例［M］.北京：国防工业出版社，2008.

［9］ 陈德民，槐创锋.精通ADAMS2005/2007虚拟样机技术［M］.北京：化学工业出版社，2010.