高频表面波对定常Ekman流解的影响*

徐俊丽 宋金宝



高频表面波对定常Ekman流解的影响*

徐俊丽1,2宋金宝1①

(1. 中国科学院海洋研究所 青岛 266071; 2. 中国科学院大学 北京 100049)

基于Jenkins(1989)建立的包含Stokes漂流、风输入和波耗散影响的修正Ekman模型, 采用Paskyabi等(2012)使用的推广的Donelan等(1987)中的谱和波耗散函数, 并利用Paskyabi等(2012)中修正方法给出的包含高频波的风输入函数, 在粘性不依赖于水深及粘性随深度线性变化的条件下, 研究了包含高频毛细重力波的随机表面波对Stokes漂流和Song(2009)导出的波浪修正定常Ekman流解的影响。结果表明高频表面波使Stokes漂流在海表面剪切加强, 对定常Ekamn流解的影响通常不能忽略, 但对Ekman流场的角度偏转影响很小。最后, 将考虑高频表面波尾谱影响所估算的定常Ekman流解与已有观测结果以及经典Ekman解进行了比对分析。

高频波; 定常Ekman流解; Stokes漂流; 风输入; 波耗散

海表面层是动量输送、热量输送和水汽输送非常活跃的区域, 对气候变化、环境污染和生物过程等有十分重要的作用。而发生在海气界面的表面波对近表层动力学过程有重要影响, 如: 波浪破碎将加强海表层的湍流混合, 波浪诱导产生的Stokes漂流以及波流相互作用产生的Langmuir环流直接影响和修正着平均流场, 波浪同时也直接影响着海表面粗糙度等。通常, 海浪运动很不规则, 可以看作由很多不同波高和波长的规则波叠加而成而用海浪谱来描述, 分析海浪谱中各成分波对界面过程的影响有助于深入了解海气界面的物理过程。海浪中的低频波有较大波高, 对海气界面流场结构有较大影响, 而高频波对动量交换起主要作用(张子范等, 1997)。

近年来, 国内外学者就波浪对Ekman流场的影响进行了大量研究。Lewis等(2004)通过考虑Stokes- Coriolis力, 研究了表面波对定常Ekman流场的影响。结果表明: Stokes漂流对定常Ekman流场的角度偏转有重要作用。Song(2009)在Lewis等(2004)研究工作的基础上, 进一步考虑了风输入项和波能耗散项的作用, 得到的结果与Lewis等(2004)的结果相比, 更接近于观测结果。Stokes漂流、风输入和波浪耗散对定常Ekman流场的修正很大程度上缩小了经典Ekman解和已有观测之间的差距。然而, 这些结论都只是在一定频率的重力波范围内得到的, 没有考虑高频毛细重力波的影响。

本文将研究包含高频毛细重力波的随机表面波对Stokes漂流和定常Ekman流解的影响。研究采用推广的DP谱以及Jenkins(1989)所建立的包含Stokes漂流、风输入和波耗散影响的修正Ekman模型。推广的DP谱是Paskyabi等(2012)中给出的包含高频波的频率谱, 频率上限可取到10Hz, 对应波长约为0.016m。因此, 采用推广的DP谱研究高频波对Stokes漂流和定常Ekman流解的影响包含了毛细重力波的作用。修正Ekman模型中的波耗散函数采用Paskyabi等(2012)中的波耗散表达式, 风输入函数采用Paskyabi等(2012)中类似的修正方法给出的包含高频波的形式。在粘性不依赖于水深及粘性随深度线性变化的条件下, 分析高频波尾谱对Stokes漂流和定常Ekman流解的影响, 并将计算结果与观测结果作一比较。

1 定常Ekman流解

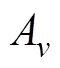
1.1 涡粘系数不依赖于水深

当涡粘系数A不依赖于水深时,A采用Ekman (1905), Santiago-Mandujano等(1990)给出的形式, 即:

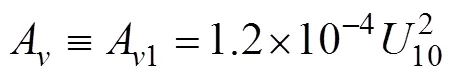
这里10为离水体表面10m高处的风速。

相应的波浪修正的定常Ekman流解表达式为(Song, 2009),

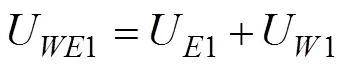
其中,

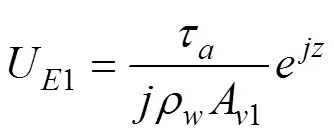
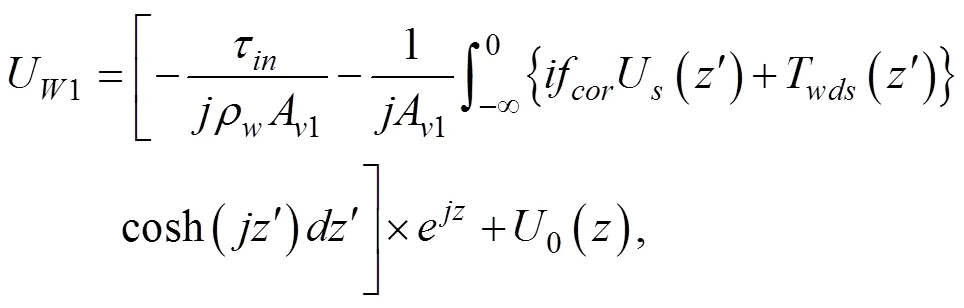
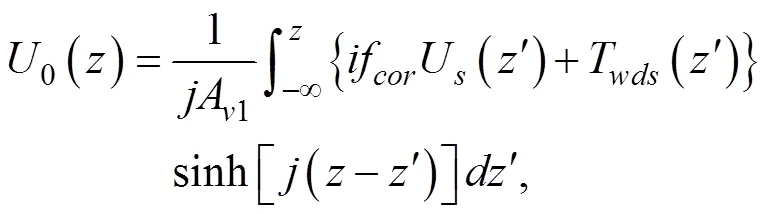
这里, (3)是经典Ekman解, (4)是风生表面波对经典Ekman解的修正部分,为深度。水体密度= 1025kg·m-3, 风应力为:

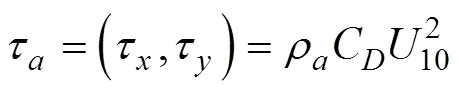
其中, 空气密度= 1.2kg·m-3,C是海气拖曳系数。

参量为:

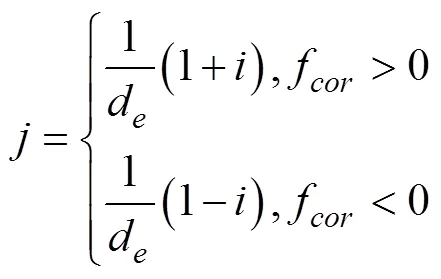
是波应力,T是波能耗散引起的波向平均流的动量输送。根据风输入函数S(,)和波浪耗散函数S(,)给出这两项表达式(Jenkins, 1989; Tang, 2007),

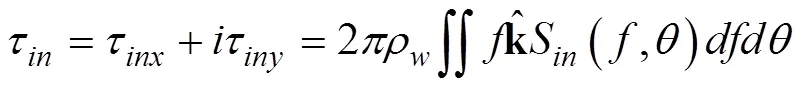
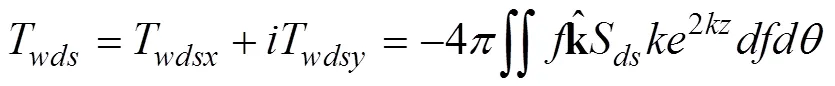
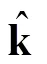
根据Kenyon(1969)和Huang(1971), Stokes漂流u为:

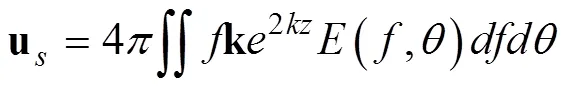
这里, k = (cos,sin)是波数向量,(,)是波浪方向频谱。

1.2 涡粘系数随深度线性变化

当涡粘系数A随深度线性变化时, 采用Madsen (1977), Lewis等(2004)给出的形式, 即:

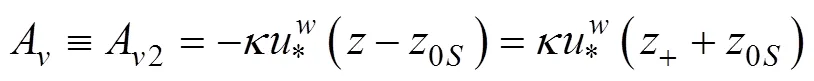
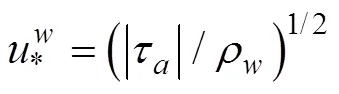
于是, 相应的波浪修正的定常Ekman流解表达式为(Song, 2009),

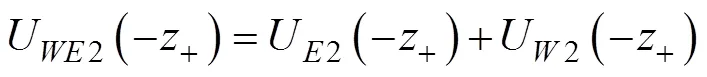
其中,

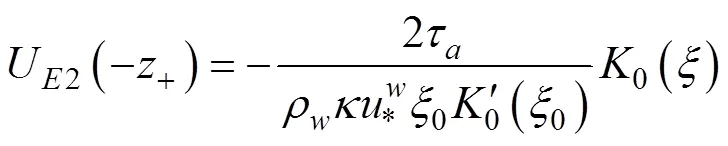
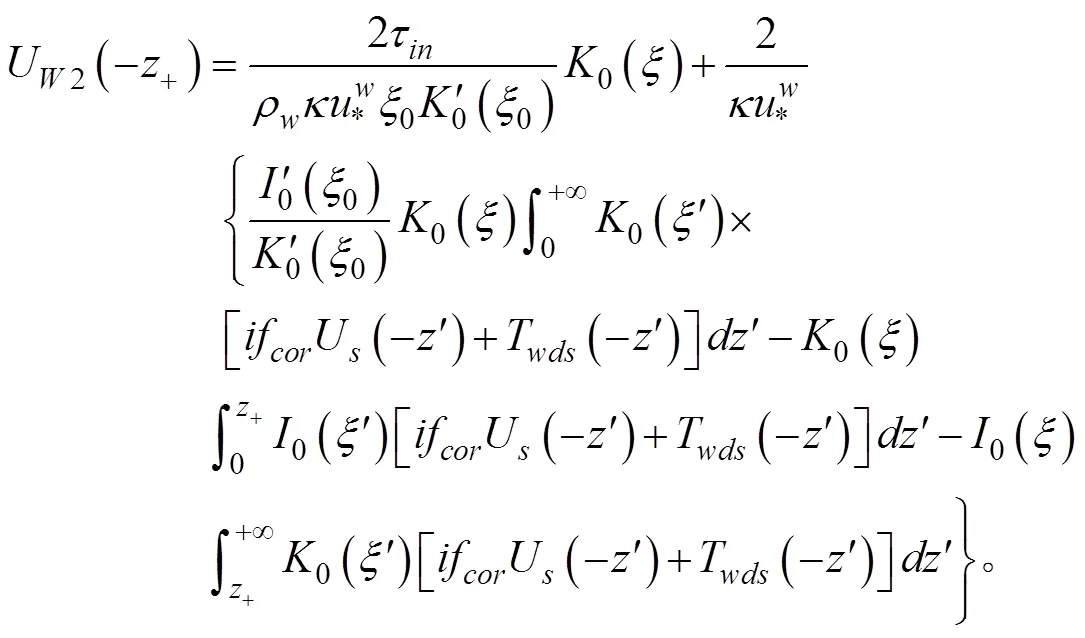
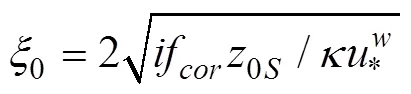
2 谱形的选取

Song(2009)采用Donelan等(1987)给出的波数方向谱(记为DP谱)分析了随机表面波对定常Ekman流解的影响, 结果表明: 考虑波浪影响的定常Ekman流解与经典Ekman解相比更接近观测结果, 但文中没有考虑高频毛细重力波的作用。本文将采用推广的DP谱(Paskyabi, 2012)来研究包含高频毛细重力波的随机表面波对定常Ekman流解的影响。推广的DP谱(简称EDP谱)定义为: 当频率≤max时使用DP谱, 而当>max时假定谱与-5成比例, 具体形式如下:

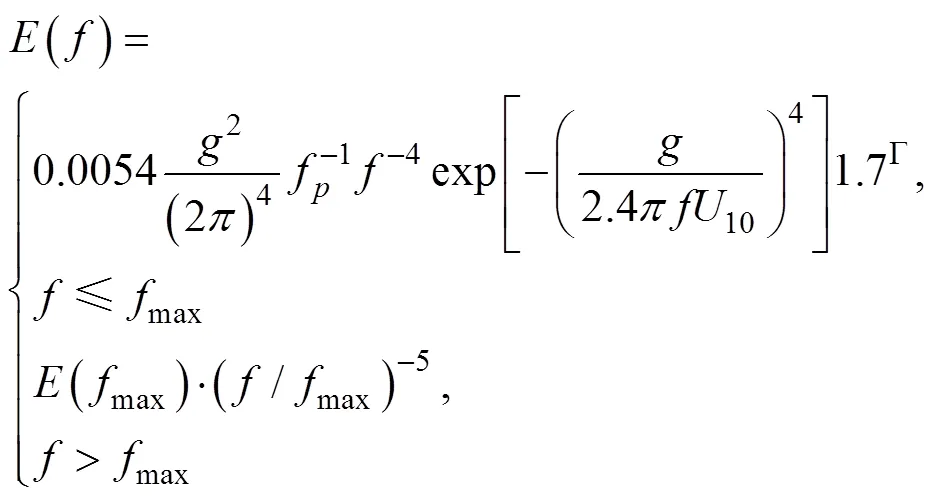
其中,

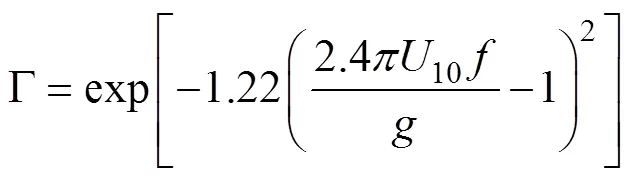
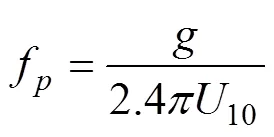
EDP谱的方向分布函数(,)为

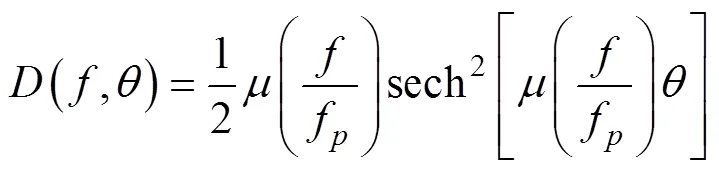
这里,

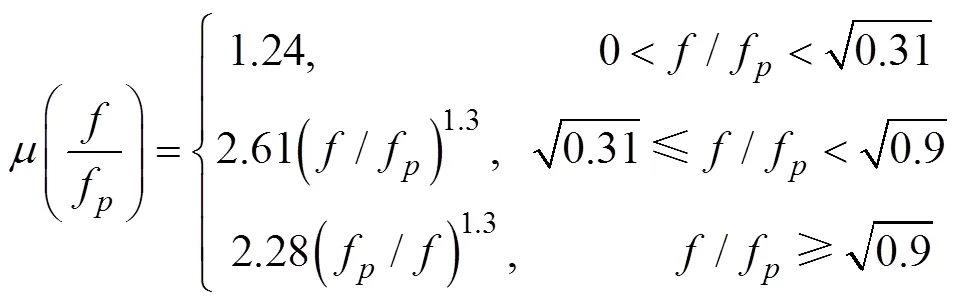
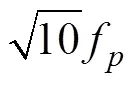
3 风输入函数和波耗散函数的选取

Song(2009)在10倍谱峰波数范围内考虑了波浪对定常Ekman流解的影响, 使用了风输入函数S(Has­se­lmann, 1988)和波浪耗散函数S(Hasselmann, 1988; Komen, 1994)。而当考虑包含高频毛细重力波的随机表面波对定常Ekman流解的影响时, 就要对相应的风输入函数作修正。本文采用修正函数()对风输入函数S() (Hasselmann, 1988)的高频部分作类似于Paskyabi等(2012)所采用的修正。

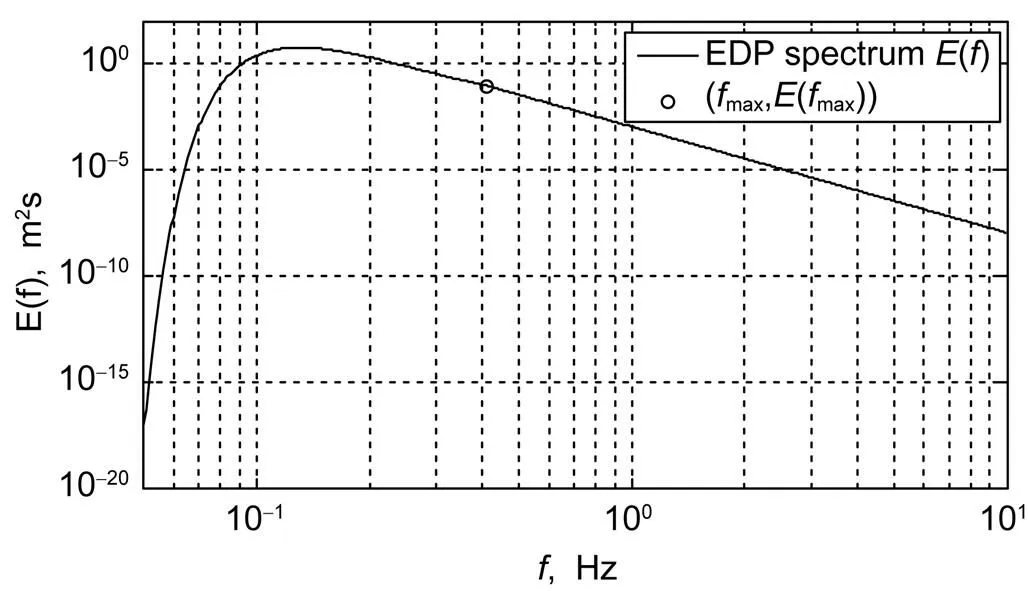
图1 在风速u10=10m/s时, 完全发展海况下EDP谱随频率f的变化, (fmax, E(fmax))是EDP谱在频率为处的分界点

风输入源项S() (Hasselmann, 1988)为

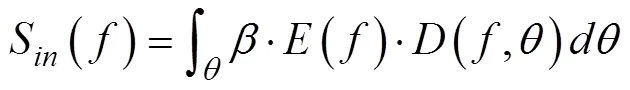
其中, 波浪增长率为

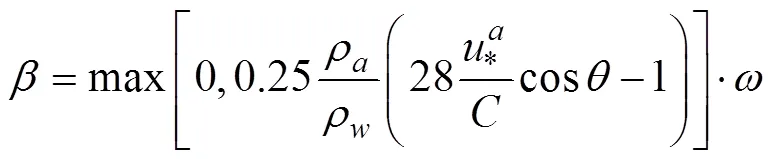
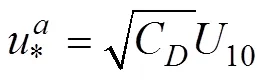
此外，按时预防接种，加强锻炼，多晒太阳，注意室内通风和保持一定湿度，及时增减衣物，营养均衡等都非常重要。

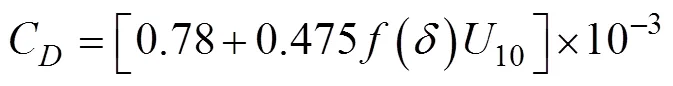
风输入源项的修正函数()形式如下:

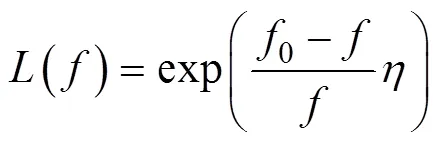
这里0是确定修正函数的起始频率, 此处取为1.35f(Tsagareli, 2008)。是修正率, 即

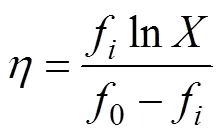
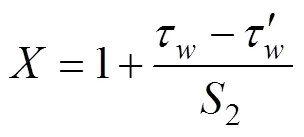
这里, 波致应力为

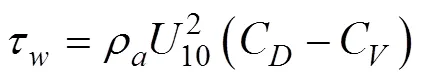
其中, 粘性拖曳系数C(Banner, 1998)为

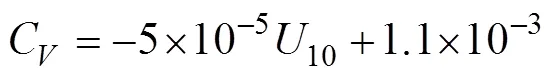
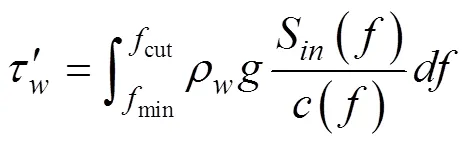
2定义为

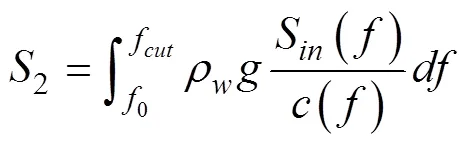
波浪耗散函数取为如下形式(Hasselmann, 1988; Komen, 1994)

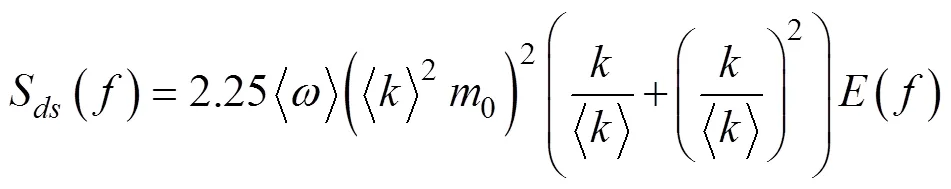
这里,

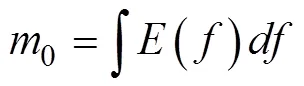
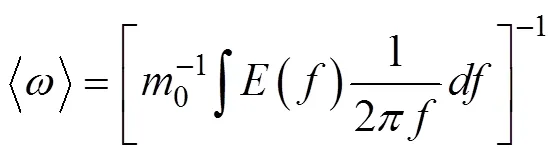
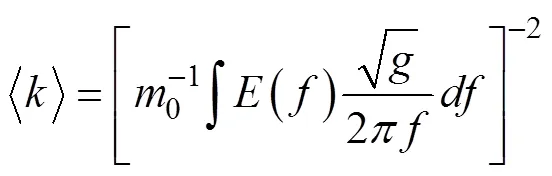
4 高频波对Stokes漂流的影响

Stokes漂流是由水质点轨迹不封闭产生, 引起海水向一定方向运输。Stokes漂流在近表

面处有很强的剪切, 因为每个波分量对Stokes漂流速度的贡献都随着Stokes深度指数衰减。而高频波对Stokes漂流也有较大贡献, 但仅限于近表面处(如图2)。该结果类似于Rascle等(2006)中的Figure 2.1。

在完全发展海况下, 利用EDP谱计算风速10= 10m/s时Stokes漂流在截断频率范围和全频范围内海表处速度值分别为0.1184m/s和0.1301m/s, 后者比前者增大9.88%。当风速10= 20m/s时, 海表处速度值分别为0.2358m/s和0.2588m/s, 后者比前者增大9.75%。而Stokes输送

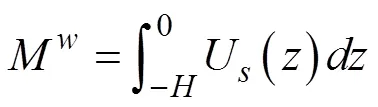
由高频波所引起的增加大约为1.3%, 几乎可以忽略。

5 高频波对定常Ekman流解的影响

5.1 高频波对涡粘系数不依赖于水深时定常Ekman流解的影响

当涡粘系数取常数时, 方程复数解(2)—(5)的实部和虚部可表示为:

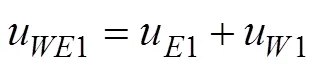
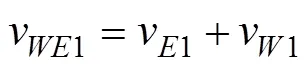
这里,u1和v1是经典Ekman解,u1和v1是Stokes漂流、风输入和波浪耗散的修正部分。

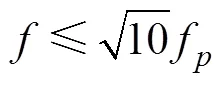
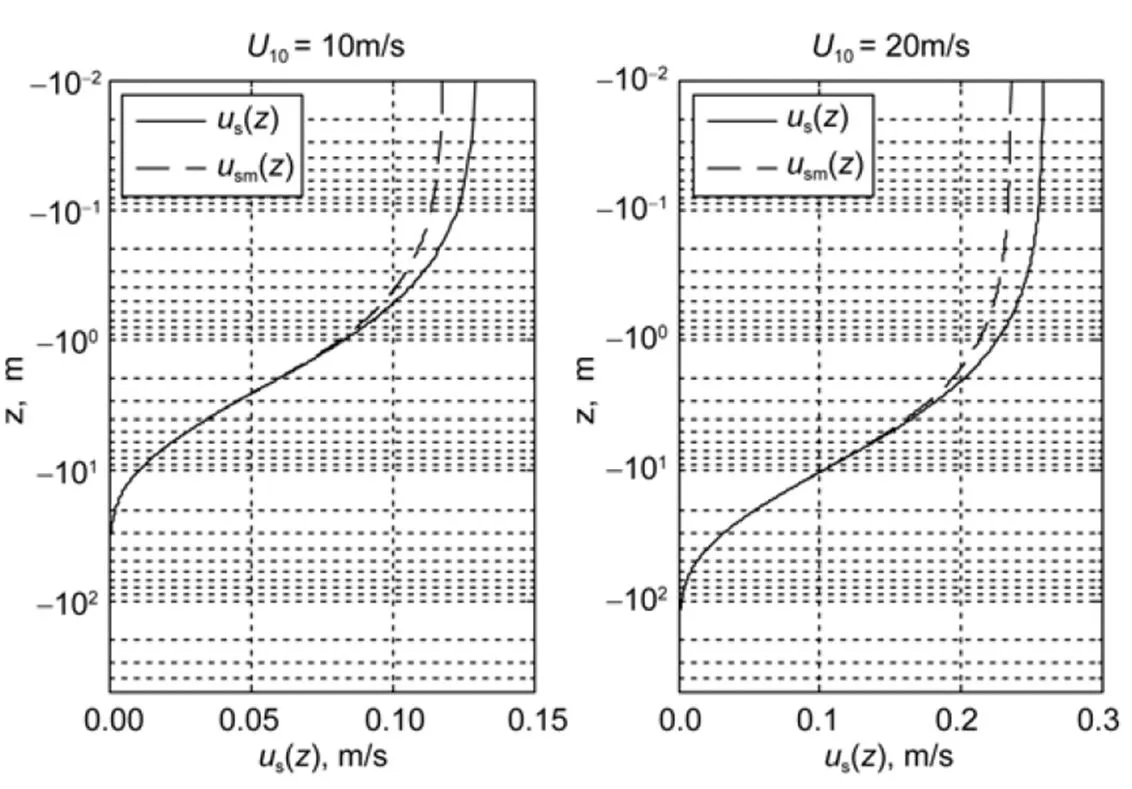
图2 当风速U10 = 10m/s (左图)和U10 = 20m/s (右图)时, Stokes 漂流速度随深度的变化。usm(z)代表截断频率范围( 10 p f ≤ f )估算的Stokes 漂流速度, 对应的最小波长为9.23m; us(z)代表全频范围估算的Stokes 漂流速度, 对应的最小波长为0.016m

5.2 高频波对涡粘系数随深度线性变化时定常Ekman流解的影响

当涡粘系数随深度线性变化时, 方程复数解 (12)—(14)的实部和虚部可如下表示,

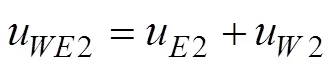
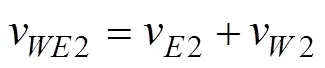
这里,u2和v2是经典Ekman解,u2和v2是Stokes漂流、风输入和波浪耗散的修正部分。

记u2和v2为截断频率范围内方程解的实部和虚部(即Song(2009)给出的解),u2和v2为全频范围内方程解的实部和虚部,u2,u2和u2分别为经典解、截断频率范围内解以及全频范围内解的大小。图7—图10显示了它们在风速10=10m/s和20m/s时的变化。

与前一小节比较可见, 涡粘系数的垂向结构对定常Ekman流解的影响很明显。当涡粘系数随深度线性变化时, 在风速分别取10m/s和20m/s的情况下, 考虑高频波之后流场在海表处的速度大小分别增加了27.29%和17.17%。在Ekman层深度d内, 流场速度大小的均方根误差分别为0.0032和0.0129。同样地, 海表面处的角度偏转受高频波影响不大, 分别由37.53°和45.53°变化到35.65°和43.57°。

6 与已有观测结果的比较

与Song(2009)一样, 本文也将包含高频波影响的定常Ekman流解与LOTUS3(the Long-Term Upper- Ocean Study)和EBC(the Eastern Boundary Current)观测结果(Price, 1999)的比较。LOTUS3数据取自1982年夏季160天西Sargasso海34°N, 70°W处, 平均风应力为0.07Pa。EBC数据取自1993年4月8日到10月20日(共6个月)位于距北California海岸400m处(37°N, 128°W)停泊的ADCP和浮标观测, 平均风应力为0.09Pa。

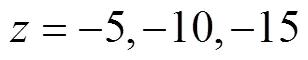
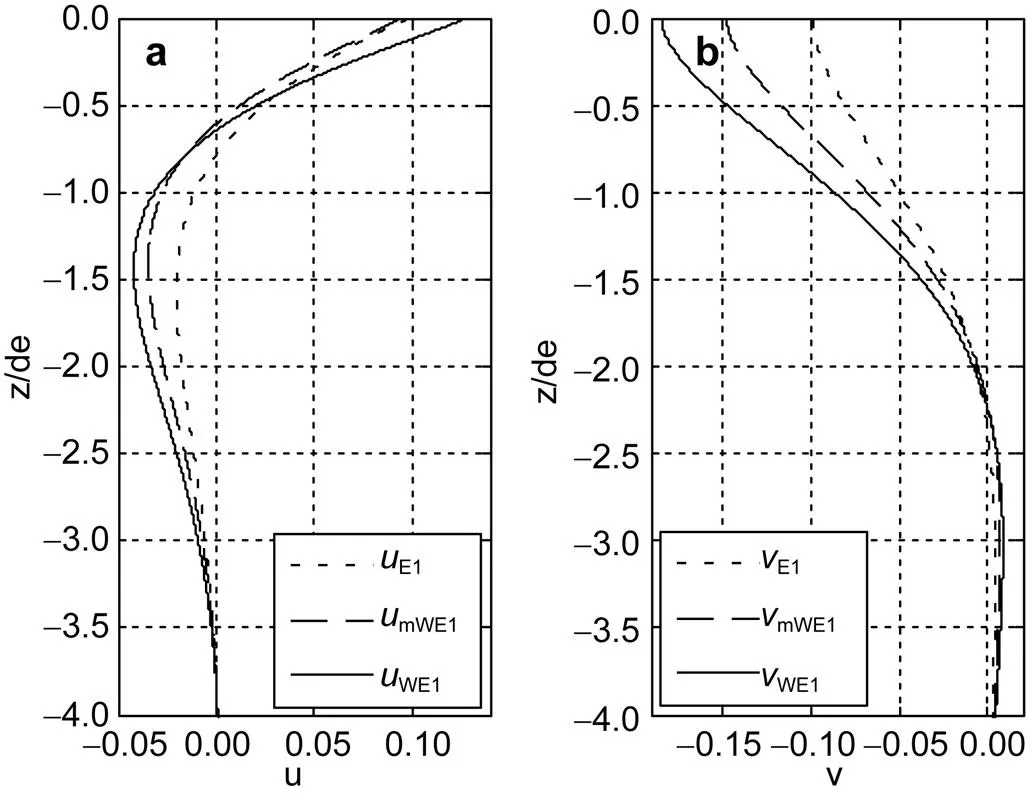
图3 当风速u10 = 10m/s时, (a) uE1, umWE1, uWE1; (b) vE1, vmWE1, vWE1的变化

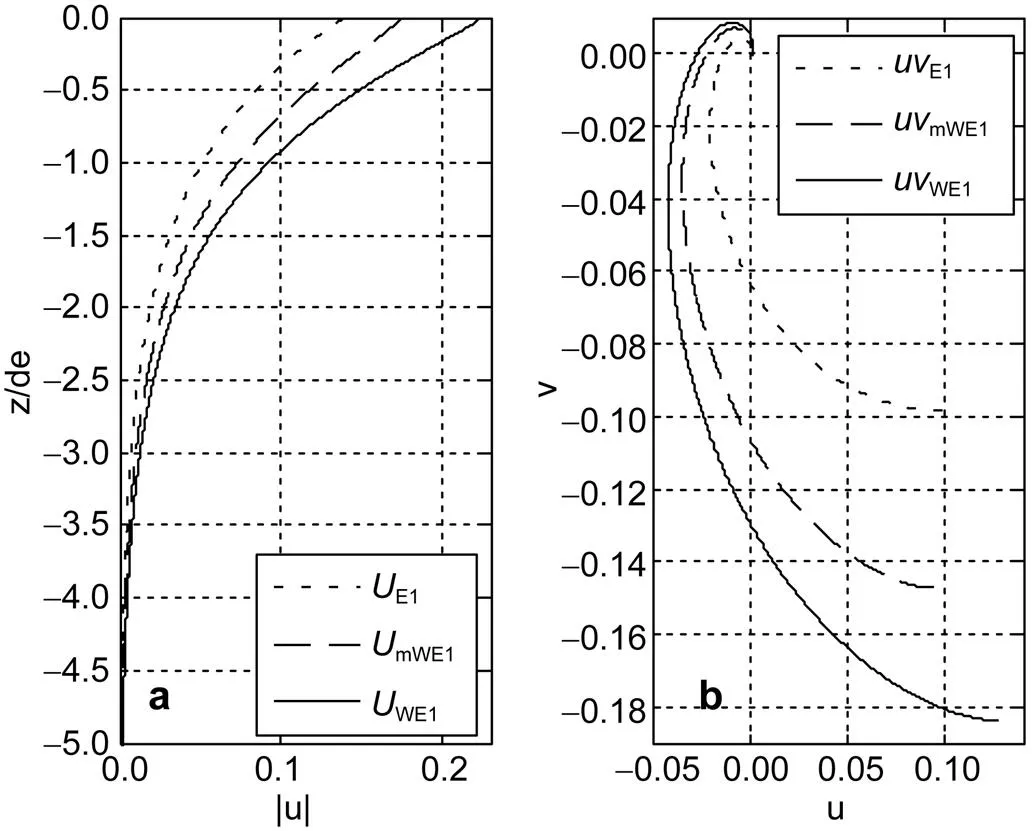
图4 当风速u10 = 10m/s时, (a) uE1,umWE1和uWE1随无因次深度z/de的变化; (b) 速度向量的矢端曲线

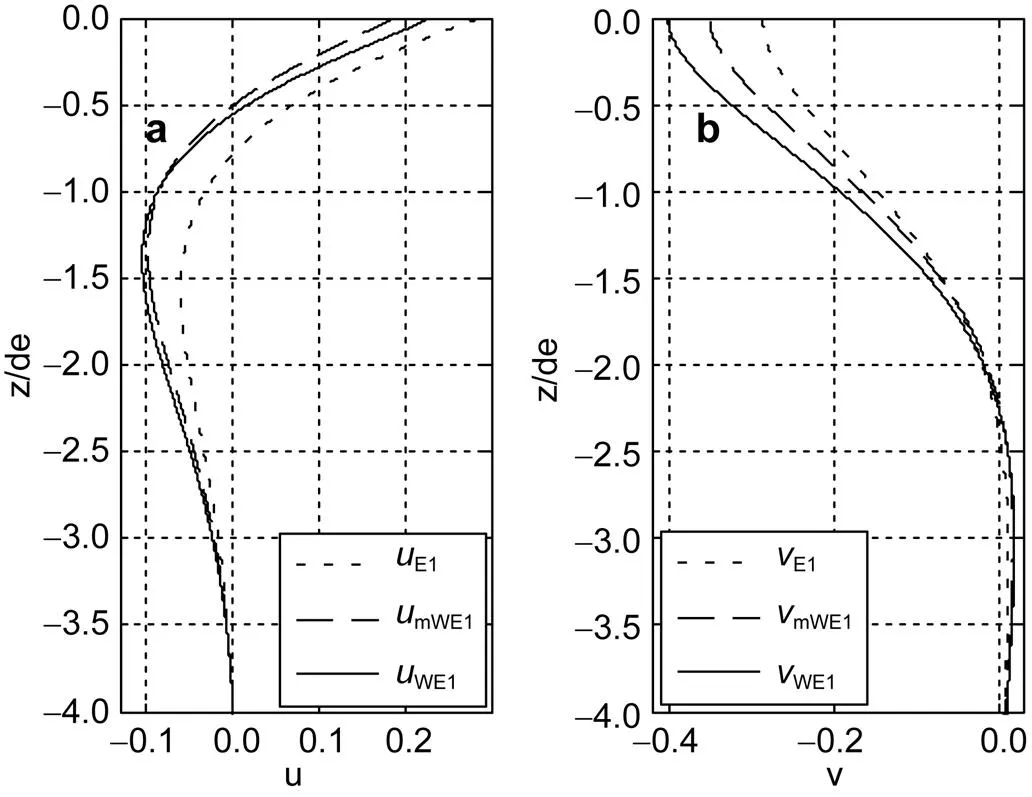
图5 当风速u10 = 20m/s时, (a) uE1, umWE1, uWE1; (b) vE1, vmWE1, vWE1的变化

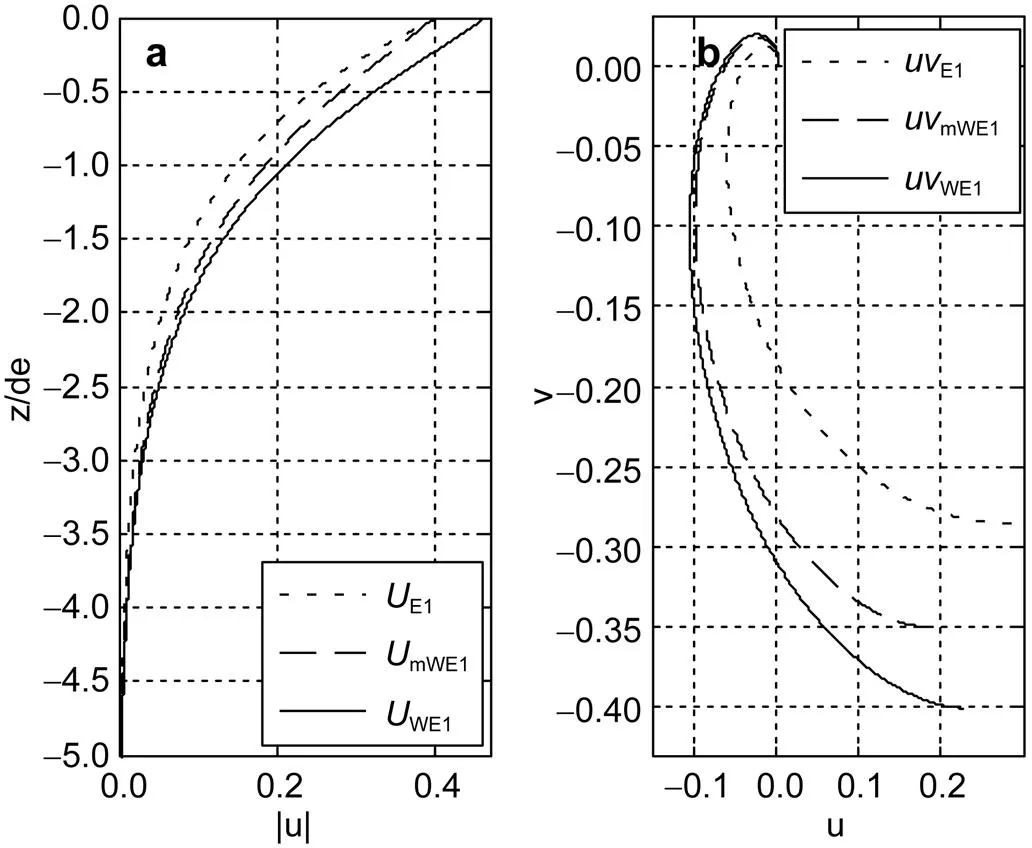
图6 当风速u10 = 20m/s时, (a)UE1, UmWE1和UWE1随无因次深度z/de的变化; (b) 速度向量的矢端曲线

7 结论与讨论

本文利用推广的DP谱, 在涡粘系数取两种不同情况时, 研究了包含高频毛细重力波的随机表面波对Stokes漂流和波浪修正的定常Ekman流解的影响, 并将该解与观测结果作了比较。结果表明, 高频波对Stokes漂流在近海表处的影响可达9%以上, 并且风速增大时Stokes漂流速度也增大。当涡粘系数取两种不同情况时, 高频波对定常Ekman流解的影响通常不能忽略, 且当风速变大时近表层流速也变大。与观测结果的比较可以看出, 考虑了高频波尾谱影响的解与观测值相比在顺风向(方向)的速度值与观测结果相比偏大, 而在近表层侧风向(方向)的速度值更接近观测结果。导致顺风向速度值与观测结果相比偏大的主要原因可能是我们采用了特定形式的涡粘性系数。当然, 下面提到的其它因素也会对解的特征产生影响。

到目前为止, 关于包含高频波影响的海浪谱还有一些其它的形式, 如Kudryavtsev等(1999, 2003)给出了含有毛细重力波的全波数方向谱, Tsagareli等(2010)根据JONSWAP谱和DHH谱(Donelan, 1985)计算了全频范围内修正的风输入函数, Babanin等(2010)在DHH谱的基础上给出了全频率范围内的联合波浪谱。因此, 探讨谱形对上述结果的影响也是必要的。

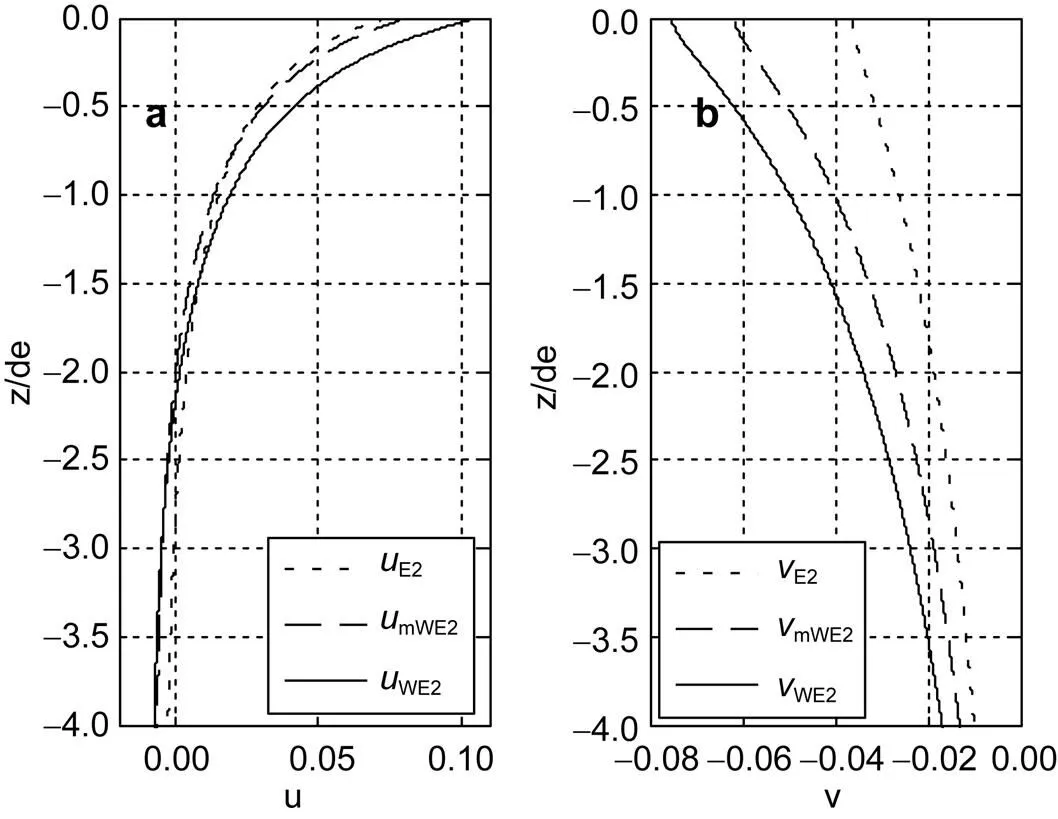
图7 当风速u10 = 10m/s时, (a) uE2, umWE2, uWE2; (b) vE2, vmWE2, uWE2的变化

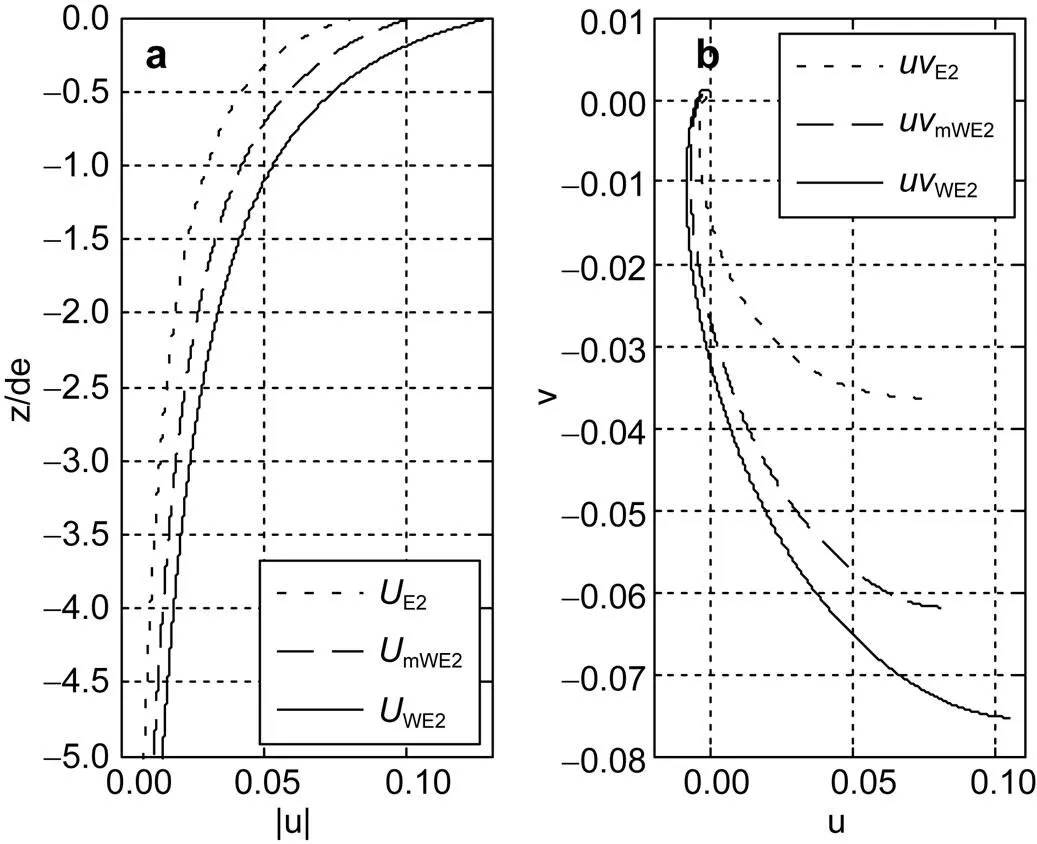
图8 当风速u10 = 10m/s时, (a) UE2, UmWE2和UWE2随无因次深度z/de的变化; (b) 速度向量的矢端曲线

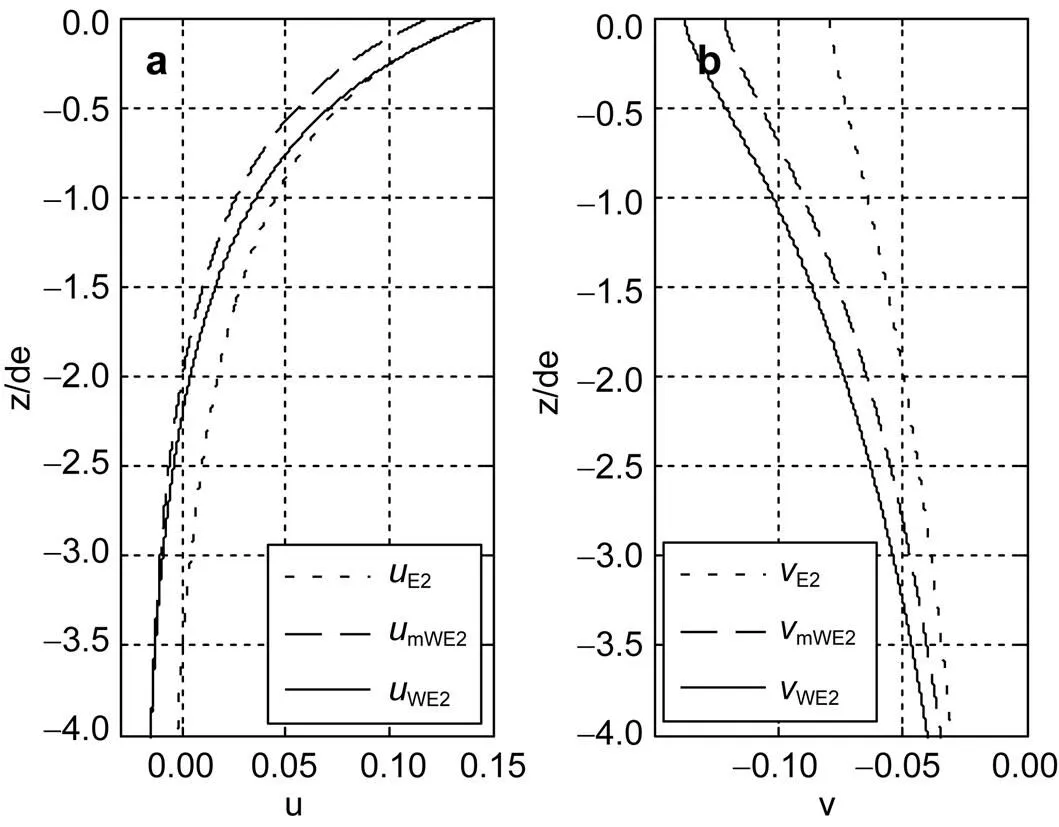
图9 当风速u10 = 20m/s时, (a) uE2, umWE2, uWE2; (b) vE2, vmWE2, vWE2的变化

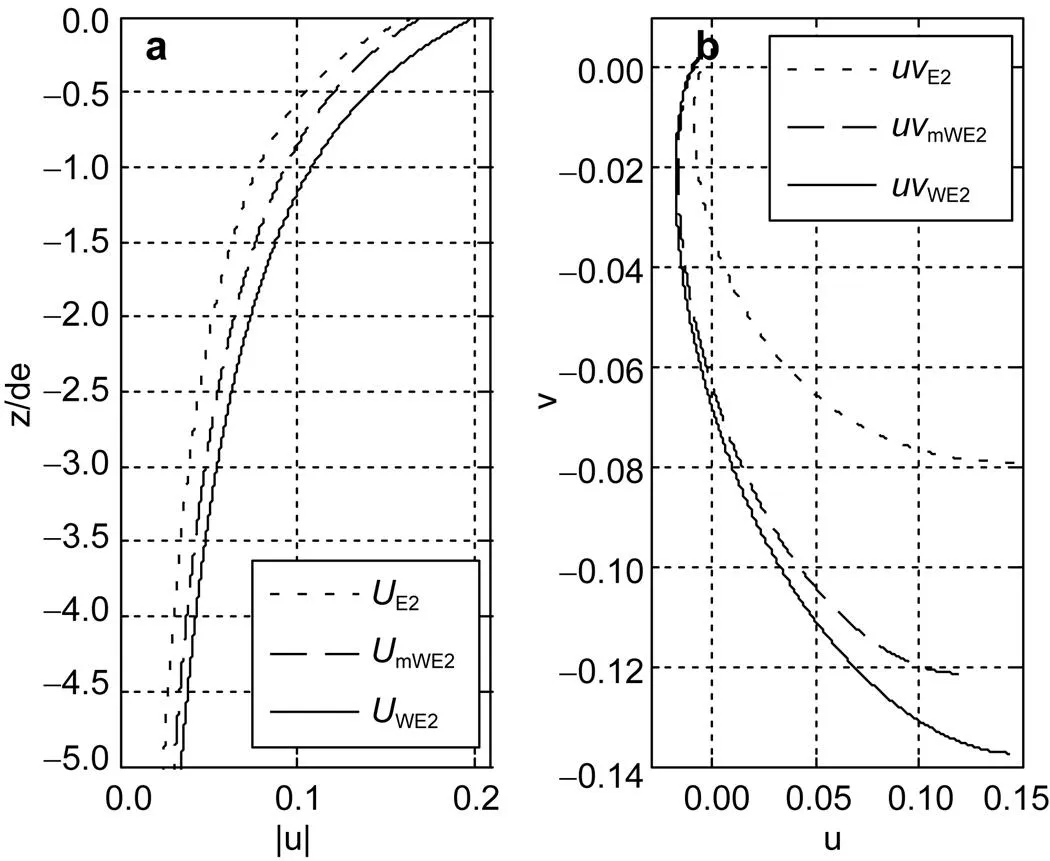
图10 当风速u10 = 20m/s时, (a) uE2,umWE2和uWE2随无因次深度z/de的变化; (b) 速度向量的矢端曲线

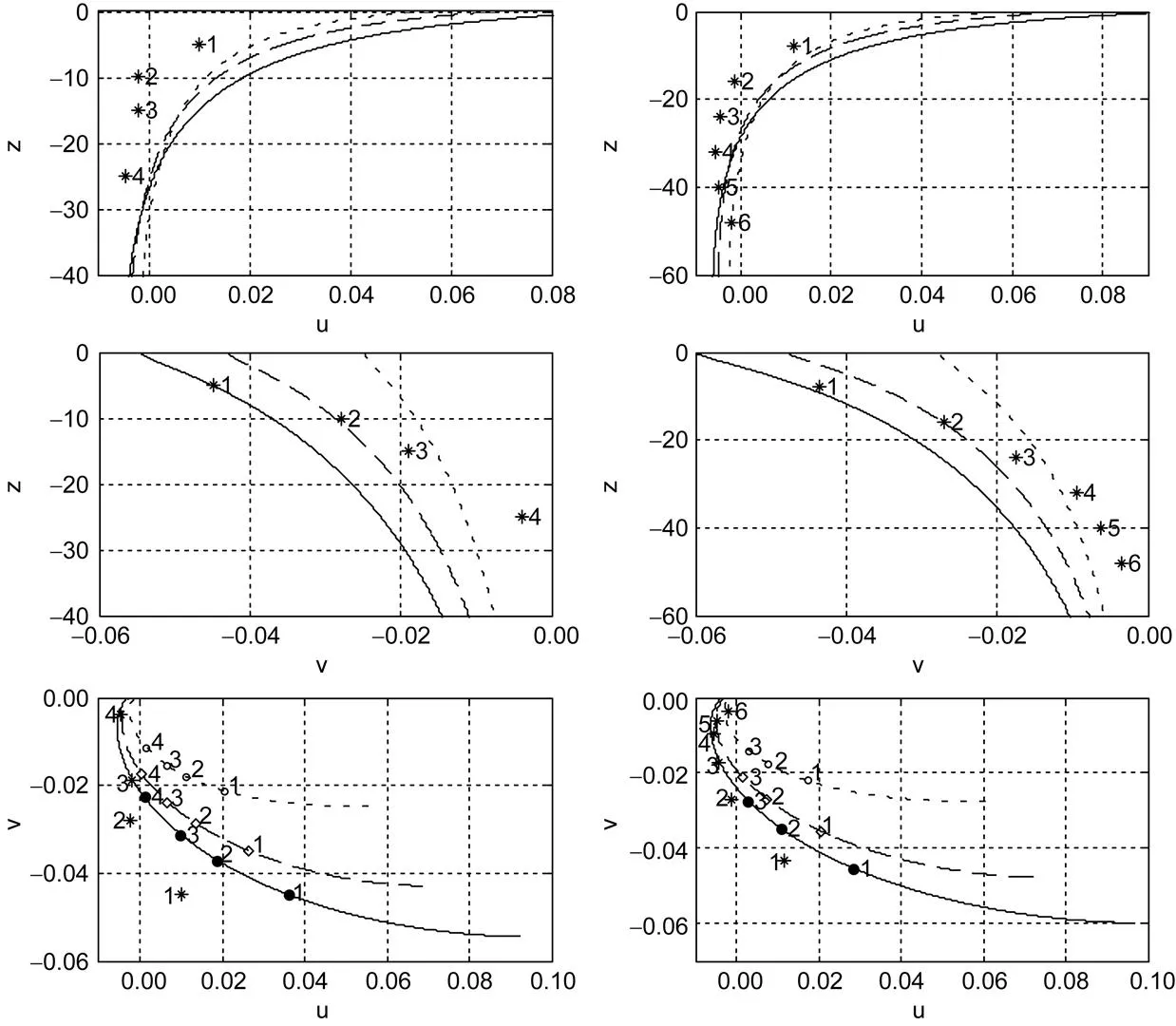
图11 方程解与LOTUS3(左边)和EBC(右边)数据(用*表示)的比较

实验数据点的深度用数字表示。点线表示经典Ekman解(u,v), 虚线表示截断频率范围内方程的解(u,v) (即Song(2009)给出的解), 实线表示全频范围内方程的解(u,v)。最上图表示顺风速度随深度变化, 中间图表示侧风速度随深度变化, 下图表示顺风速度与侧风速度的矢端曲线

在计算高频表面波对定常Ekman流解的影响时, 很多因素被忽略掉了, 如密度分层、表面加热、浮力通量和科氏参量的水平分量等。这些因素在一定条件下可能是重要的, 本文不作具体讨论。

张子范, 李家春, 1997. 风浪充分发展下海面阻力系数的数值研究. 力学学报, 29(4): 385—394

Babanin A V, Tsagareli K N, Young I R et al, 2010. Numerical investigation of spectral evolution of wind waves. Part II: Dissipation term and evolution tests. J Phys Oceanogr, 40(4): 667—683

Banner M L, Peirson W L, 1998. Tangential stress beneath wind-driven air-water interfaces. J Fluid Mech, 364(01): 115—145

Donelan M A, Hamilton J, Hui W H, 1985. Directional spectra of wind-generated waves. Phil Trans R Soc Lond, 315(1534): 509—562

Donelan M A, Pierson W J, 1987. Radar scattering and equilibrium ranges in wind-generated waves with application to scatterometry. J Geophys Res, 92(C5): 4971— 5029

Ekman V W, 1905. On the influence of the earth’s rotation on ocean currents. Arch Math Astron Phys, 2: 1—52

Guan C L, Xie L, 2004. On the linear parameterization of drag coefficient over sea surface. J Phys Oceanogr, 34(12): 2847—2851

Hasseimann K, and Coauthors, 1988. The WAM model—A third generation ocean wave prediction model. J Phys Oceanogr, 18(12): 1775—1810

Huang N E, 1971. Derivation of Stokes drift for a deep-water random gravity wave field. Deep-Sea Res, 18(2): 255—259

Jenkins A D, 1989. The use of a wave prediction model for driving a near surface current model. Dtsch Hydrogr Z, 42(3—6): 134—149

Kenyon K E, 1969. Stokes drift for random gravity waves. J Geophys Res, 74(28): 6991—6994

Komen G J, Cavaleri L, Donelan M, 1994. Dynamics and Modelling of Ocean Waves. Cambridge University Press, 1—532

Kudryavtsev V N, Makin V K, Chapron B, 1999. Coupled sea surface-atmosphere model. 2. Spectrum of short wind waves. J Geophys Res, 104(C4): 7625—7639

Kudryavtsev V N, Hauser D, Caudal G et al, 2003. A semiempirical model of the normalized radar cross-section of the sea surface 1. Background model. J Geophys Res, 108(C3), 8055,

Lewis D M, Belcher S E, 2004. Time-dependent, coupled, Ekman boundary layer solutions incorporating Stokes drift. Dyn Atmos Oceans, 37(4): 313—351

Madsen O S, 1977. A realistic model of the wind-induced Ekman boundary layer. J Phys Oceanogr, 7(2): 248—255

Mellor G, Blumberg A, 2004. Wave breaking and ocean surface layer thermal response. J Phys Oceanogr, 34(3): 693—698

Paskyabi M B, Fer I, Jenkins A D, 2012. Surface gravity wave effects on the upper ocean boundary layer: Modification of a one-dimensional vertical mixing model. Continental Shelf Research, 38: 63—78

Price J F, Sundermeyer M A, 1999. Stratified Ekman layers. J Geophys Res, 104(C9): 20467—20494

Rascle N, Ardhuin F, Terray E A, 2006. Drift and mixing under the ocean surface: A coherent one-dimensional description with application to unstratified conditions. J Geophys Res, 111, C03016, doi:10.1029/2005JC003004

Santiago-Mandujano F, Firing E, 1990. Mixed-layer shear generated by wind stress in the central equatorial Pacific. J Phys Oceanogr, 20(10): 1576—1582

Song J B, 2009. The effects of random surface waves on the steady Ekman current solutions. Deep-Sea Research I, 56(5): 659—671

Tang C L, Perrie W, Jenkins A D, 2007. Observation and modeling of surface currents on the Grand Banks: a study of the wave effects on surface currents. J Geophys Res, 112, C10025, doi:10.1029/2006JC004028

Tsagareli K, 2008. Numerical investigation of wind input and spectral dissipation in evolution of wind waves. Ph.D. thesis, University of Adelaide

Tsagareli K N, Babanin A V, Walker D J, Young I R, 2010. Numerical investigation of spectral evolution of wind waves. Part I: Wind-input source function. J Phys Oceanogr, 40(4): 656—666

EFFECTS OF HIGH FREQUENCY SURFACE WAVES ON THE STEADY EKMAN CURRENT SOLUTIONS

XU Jun-Li1,2, SONG Jin-Bao1

(1. Institute of Oceanology, Chinese Academy of Sciences, Qingdao 266071, China; 2. University of Chinese Academy of Sciences, Beijing 100049, China)

Based on the wave-modified Ekman model including the Stokes drift, wind input, and wave dissipation by Jenkins (1989), the effects of high frequency surface waves (including the short waves in capillary wave range) on the Stokes drift, and analytic steady solutions of wave-modified Ekman equation are studied. The steady solutions are obtained under the assumptions that eddy viscosity is independent of depth; and eddy viscosity increases linearly with depth using generalized Donelan and Pierson (1987) spectrum, wave dissipation of Paskyabi(2012), and modified wind input that is similar to Paskyabi(2012). The results demonstrate that high-frequency surface waves strengthen the shear of the Stokes drift at the sea surface and the effects on the Ekman solutions should not be neglected. However, the effect of angular turning on the sea surface is very small. In addition, the wave-modified solutions obtained by including high frequency waves are compared with the observations and the classical Ekman solution.

high frequency waves; steady Ekman current solutions; Stokes drift; wind input; wave dissipation

10.11693/hyhz20121213001

* 国家自然科学基金项目, 41176016号; 国家基金委创新群体项目, 41121064号。徐俊丽, 博士研究生, E-mail: xjlshy1983@163.com

宋金宝, 研究员, E-mail: songjb@qdio.ac.cn

2012-12-13,

2013-02-05

P738.1