A Sliding Mode Control Algorithm for Solving an Ill-posed Positive Linear System

Chein-Shan Liu

1 Introduction

In this paper we propose a robust and easily-implemented algorithm to solve the following linear equations system:

whereB∈Rn×nis a given positive-definite matrix,and x∈Rnis an unknown vector to be determined from the input data b∈Rn.When B is severely ill-conditioned and b is perturbed by noise,we may encounter the problem that the numerical solution of Eq.(1)will deviate from the exact one to a great extent.Therefore,an algorithm compromises stability,efficiency and accuracy is desired.

There are several regularization techniques developed after the pioneering work of Tikhonov and Arsenin(1977).Previously,the author and his co-workers have developed several methods to solve the ill-posed linear problems:using the fictitious time integration method as a filter for ill-posed linear system[Liu and Atluri(2009a)],a modified polynomial expansion method[Liu and Atluri(2009b)],the non-standard group-preserving scheme[Liu and Chang(2009)],a vector regularization method[Liu,Hong and Atluri(2010)],the preconditioners and postconditioners generated from a transformation matrix,obtained by Liu,Yeih and Atluri(2009)for solving the Laplace equation with a multiple-scale Trefftz basis functions,the relaxed steepest descent method[Liu(2011a,2012a)],the optimal iterative algorithm[Liu and Atluri(2011a)],an optimally scaled vector regularization method[Liu(2012b)],the best vector iterative method[Liu(2012c)],a globally optimal iterative method[Liu(2012d)],the generalized Tikhonov regularization methods[Liu(2012e)],the optimal tri-vector iterative methods[Liu(2013a,2014a)],as well as an adaptive Tikhonov regularization method[Liu(2013b)].

It is known that iterative methods for solving the system of algebraic equations can be derived from the discretization of certain ODEs system[Bhaya and Kaszkurewicz(2006);Chehab and Laminie(2005);Liu and Atluri(2008)].Particularly,the descent methods can be interpreted as the discretizations of gradient flows[Brown and Bartholomew-Biggs(1989);Helmke and Moore(1994)].For a large scale system the main choice is using an iterative regularization algorithm,where a regularization parameter is presented by the number of iterations.The iterative method works if an early stopping criterion is used to prevent the reconstruction of noisy components in the approximate solutions.

Liu and Atluri(2008)have developed a very simple ODEs system for iteratively solving algebraic equations.After the work by Liu and Atluri(2008),there were several works applied the fictitious time integration method(FTIM)to solve engineering problems,e.g.,[Liu and Atluri(2009a);Liu(2008a,2009a,2009b,2009c,2010);Chi,Yeih and Liu(2009),Ku,Yeih,Liu and Chi(2009);Chang and Liu(2009)].In this paper we will develop an affine nonlinear ODEs system with a derived controller from the sliding mode control theory to accelerate the convergence speed in the solution of ill-posed linear problems.

2 An invariant manifold

There are several regularization methods to deal with Eq.(1)when B is ill-conditioned,of which the most prominent and best well understood ones are the Tikhonov method,the Landweber iteration method,and truncated singular value decomposition,all being linear and all being strongly convergent with an appropriate a priori parameter choice[Eicke,Louis and Plato(1990)].In this paper we consider an iterative regularization method for Eq.(1)by investigating

We start from a continuous manifold[Absil,Baker and Gallivan(2007);Adler,Dedieu,Margulies,Martens and Shub(2002);Baker,Absil and Gallivan(2008);Smith(1994);Yang(2007)],defined in terms of the square-residual-norm of r and a functionQ(t):

Here,we let x be a function of a fictitious time-like variablet,and expect that in our algorithmQ(t)＞0 is an increasing function oft,and the residual error can be decreased with time.We letQ(0)=1,andCis determined by the initial condition x(0)=x0given by

Usually,C＞0,andC=0 when the initial value x0is just the solution of Eq.(1).WhenC＞0 andQ＞0,the manifold defined by Eq.(3)is continuous and differentiable,and thus the following differential operation carried out on the manifold makes sense.For the requirement of"consistency condition",i.e.,x(t)always on the manifold in time,we have

which is obtained by taking the time differential of Eq.(3)with respect totand considering x=x(t).

The governing equation of x cannot be uniquely determined by Eq.(5);however,we suppose that x is governed by a gradient- flow,like that for the steepest-descent method(SDM):

where λ is to be determined.Inserting Eq.(6)into Eq.(5)we can solve

Thus by inserting the above λ into Eq.(6)we can obtain an ODEs system for x:

where

IfQ(t)can be guaranteed to be an increasing function oft,we have an absolutely convergent numerical method to solve Eq.(1)shown as follows:

Whentis large enough the above equation will enforce the residual error‖r(x)‖tending to zero,and meanwhile the solution of Eq.(1)is obtained approximately.

3 The sliding mode control method

Equation(8)is an ODEs system defined on the invariant manifold in Eq.(10).Based on this equation,Liu(2011a)has derived the relaxed steepest descent method(RSDM)for solving linear system(1).Although the original design of the numerical algorithm is for the purpose of keeping the orbit of x on the invariant manifold in Eq.(10),but in practice the RSDM cannot satisfy this requirement.For this purpose we can insert acompensated controller˜uin Eq.(8):

such that a suitable design of˜ucan help us to achieve this purpose.In above we letq=1 and r is taken as a gain vector.

The theory of sliding mode control for system(11)is designed an invariant hypersurface[Utkin(1978,1992);Liu(2014b)]:

in the state space,such that by keeping the orbit of x on the surface we require

Here we can set up the most simple sliding surface by

where a is a constant vector.Hence,we have

Inserting Eq.(11)for˙x we can derive

where

From Eq.(16)we can solve

and then by Eq.(11)we have

however,this ODEs system may be unstable.Thus we recast Eq.(19)to be

where

In the control theory,Eq.(20)is a form of anaffine nonlinear system,which is linear with the control forceu(t),while the residual vector r is acting as a gain vector.

Now we prove that the above dynamical system is asymptotically stable,tending to the zero dynamics of the residual vector r.Consider the following Lyapunov function:

Taking the derivative ofVand insertingand Eq.(20)we can derive

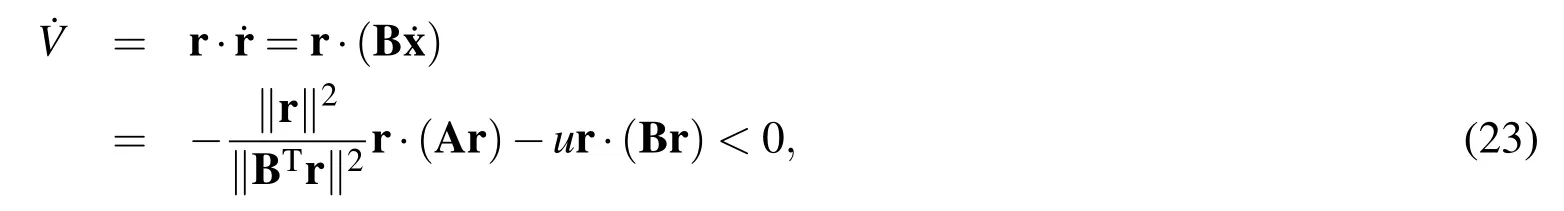
where we have used the positiveness of A,B andu.As compared with Eq.(8),the new ODEs system(20)possesses an extra termur to enforce the dynamics to the zero point of r=0,which is gained by a sliding effect with the aid of a gain vector r and a positive control forceu.

Given an initial point r0=Bx0-b we can construct the constant vector a by an arbitrarily given vector a0,say a0=(1,...,1)T:

it is obvious that a·r0=0,such thats0=a·r0=0.

We simply use the Euler scheme to integrate Eq.(20),and thus one can derive the following sliding mode control algorithm(SMCA):

(i)Give a step sizeh,an initial x0,r0=Bx0-b and a0=(1,...,1)T,and compute

(ii)Fork=0,1,2,...,we repeat the following computations:

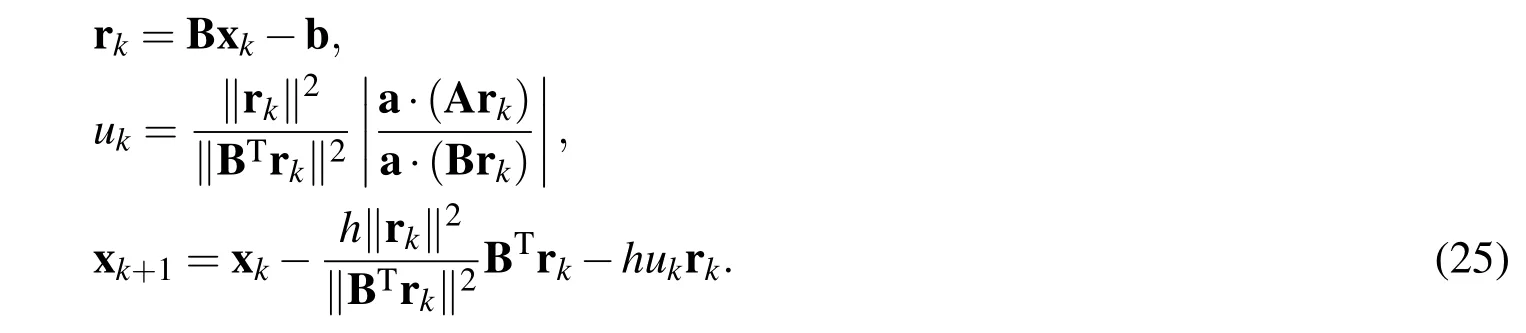
If xk+1converges according to a given stopping criterion ‖rk+1‖＜ ε,then stop;otherwise,go to step(ii).

4 Numerical examples

In order to assess the performance of the newly developed method of the sliding mode control algorithm(SMCA),let us investigate the following examples.Some results are compared with that obtained by the relaxed steepest descent method(RSDM),conjugate gradient method(CGM),the optimal iterative algorithm driven by an optimal descent vector(OIA/ODV),and the globally optimal iterative algorithm(GOIA).

4.1 Hilbert problems

Finding ann-degree polynomial functionp(x)=a0+a1x+...+anxnto best match a continuous functionf(x)in the interval ofx∈[0,1]:

leads to a problem governed by Eq.(1),where B is the(n+1)×(n+1)Hilbert matrix,defined by

x is composed of then+1 coefficientsa0,a1,...,anappeared inp(x),and

is uniquely determined by the functionf(x).

The Hilbert matrix is a famous example of highly ill-conditioned matrices.Eq.(1)with the coefficient matrix B having a large condition number usually displays that an arbitrarily small perturbation of data on the right-hand side may lead to an arbitrarily large perturbation to the solution on the left-hand side.

In this example we consider a highly ill-conditioned linear equation(1)with B given by Eq.(27).The ill-posedness of Eq.(1)with the above B increases very fast with an exponential growth withn.

4.1.1 n=9

In order to compare the numerical solutions with exact solutions we suppose thatx1=...=xn=1 to be the exact one,and then by Eq.(27)we have

where we consider noise being imposed on the data with random numbersR(i)∈[-1,1].

We first calculate this problem for the case withn=9 and σ=0.The resulting linear equation is highly ill-conditioned,since the condition number is quite large,up to 4.93×1011.

In the computation by the SMCA we have fixedh=0.3.Starting fromx1=...=x9=0.5,and with a stopping criterion ε=10-8we find that SMCA converges with 1166 iterations,where the maximum error is 1.03×10-3.

The RSDM with γ=0.06 does not converge within 5000 iterations;however the numerical solution is close to the exact solution as shown in Table 1 with the maximum error being 1.44×10-3;wherein,for the purpose of comparison,the values obtained by the conjugate gradient method(CGM)are also listed.The maximum error of CGM is 7.85×10-3.

4.1.2 n=50

Let us increase the ill-posedness of the linear Hilbert problem ton=50.For this problem the condition number is about 1.1748×1019.We first consider a constant solutionx1=...=x50=1.The convergence criterion ε is fixed to be ε=10-6for case 1 with noise-free σ =0,and case 2 with ε=10-3and with a noise σ =10-4.Starting from the initial conditionxi=0.5,i=1,...,50,for case 1 the SMCA withh=0.1 converges with 1184 iterations as shown in Fig.1(a)for the residual error,Fig.1(b)for the control force and Fig.1(c)for the numerical error,of which the maximum error is 0.00392.Very accurate result is obtained.From Fig.2(a)we can observe that the iterative dynamics approaches to the sliding surface withs=0 very quickly.For case 2 the SMCA withh=0.1 converges with 116 iterations as shown in Fig.2(b)for the sliding quantitys,Fig.2(c)for the residual error and the control force.The maximum error is 0.037 as shown in Fig.1(c)by the dashed line.

4.1.3 n=200

Let us considern=200 and with a noise σ=10-5.In the computation of this noisy problem by the SMCA,we fixh=0.35 and ε=10-3,where we show the residual error in Fig.3(a)and the SMCA converges with 82 iterations.From Fig.3(b)we can see that the sliding mode is obtained very fast.The numerical solution obtained by the SMCA converges to the exact solution very accurately as shown in Fig.3(c)with the maximum error being 0.0258.We also apply the CGM to this problem under the same noise.Under the above convergence criterion the CGM converges very fast with 9 steps,and the maximum error as shown in Fig.3(c)is 0.0993.It can be seen that the accuracy of SMCA is better than CGM.

Figure 1:For example 1 of Hilbert problem with n=50,(a)the residual and(b)the control force for noise free case,and(c)comparing the numerical errors.

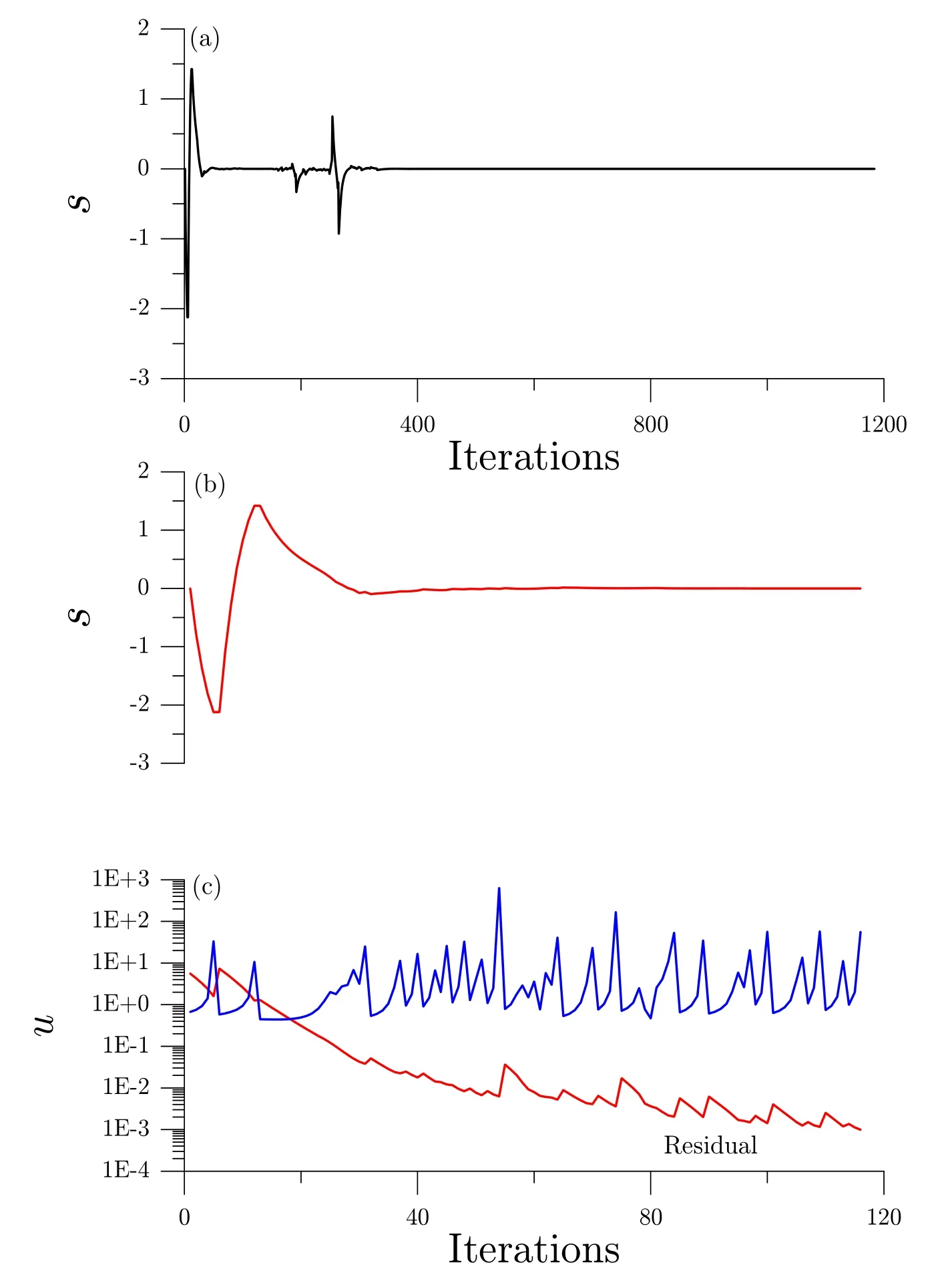
Figure 2:For example 1 of Hilbert problem with n=50,comparing the sliding quantities for(a)noise free and(b)under a noise,and(c)the control force and residual for the noised case.

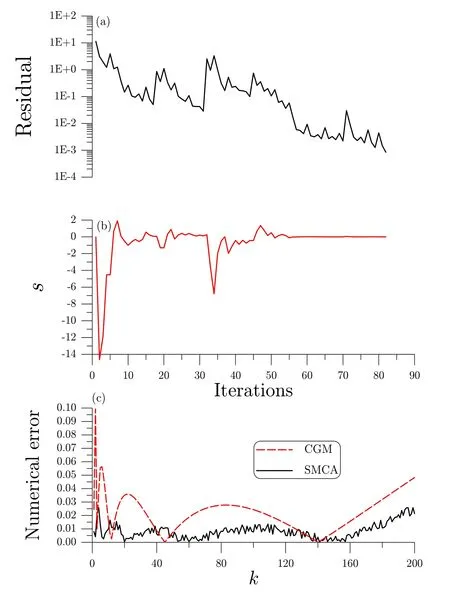
Figure 3:For example 1 of Hilbert problem with n=200,(a)the residual and(b)the sliding quantity for noised case,and(c)comparing the numerical errors.

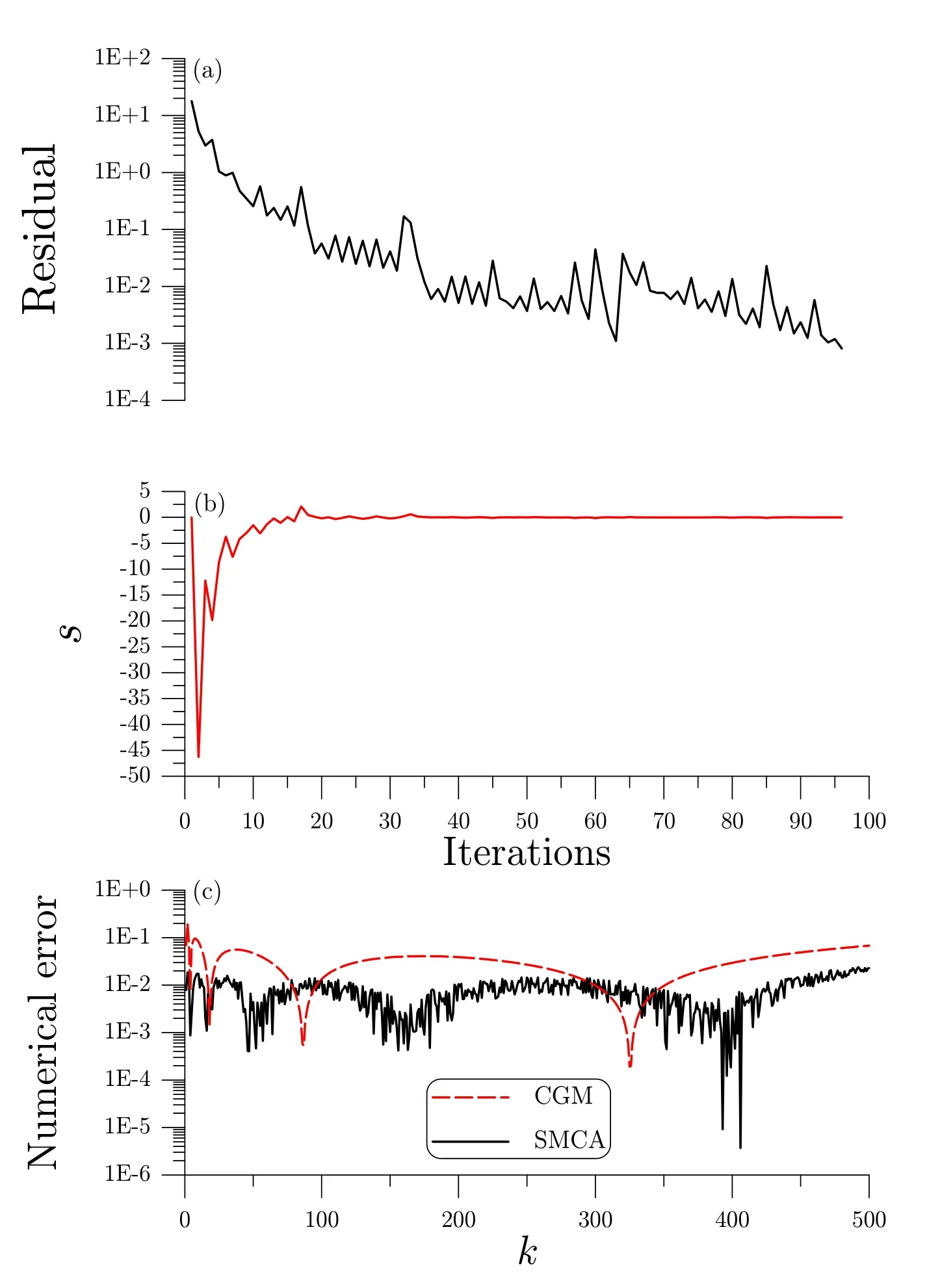
Figure 4:For example 1 of Hilbert problem with n=500,(a)the residual and(b)the sliding quantity for noised case,and(c)comparing the numerical errors.

4.1.4 n=500

Let us considern=500 and with a noise σ=10-5.In the computation by the SMCA,we fixh=0.4 and ε=10-3,where we show the residual error in Fig.4(a)and the SMCA can converge with 96 iterations.From Fig.4(b)we can see that the sliding mode is obtained very fast.The numerical solution of SMCA is very accurate as shown in Fig.4(c)with the maximum error being 0.024.The maximum error of CGM as shown in Fig.4(c)is large up to 0.1973.It can be seen that the accuracy of SMCA is much better than CGM.From the above cases for this highly ill-posed Hilbert problem we can observe that the present SMCA is robust and effective,which is insensitive to the degree of the ill-posedness.The accuracy of the SMCA is much better than other methods.

4.2 Example 2

When the backward heat conduction problem(BHCP)is considered in a spatial interval of 0＜x＜ℓ by subjecting to the boundary conditions at two ends of a slab:

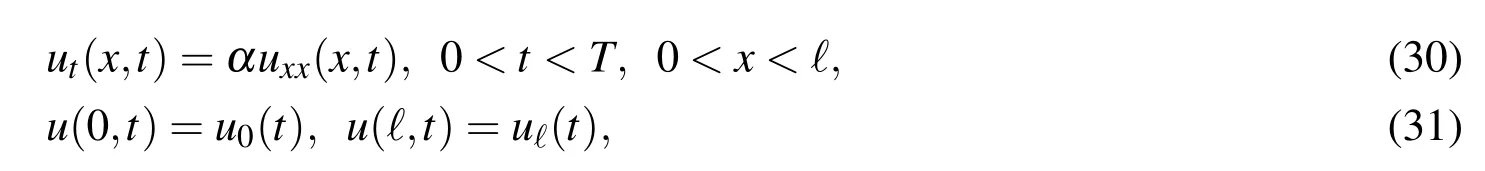
we solveuunder a final time condition:

The fundamental solution to Eq.(30)is given as follows:

whereH(t)is the Heaviside function.

The method of fundamental solutions(MFS)has a broad application in engineering computations.However,the MFS has a serious drawback in that the resulting system of linear equations is always highly ill-conditioned,when the number of source points is increased[Golberg and Chen(1996)],or when the distances of source points are increased[Chen,Cho and Golberg(2006)].

In the MFS the solution ofuat the field point z=(x,t)can be expressed as a linear combination of the fundamental solutionsU(z,sj):

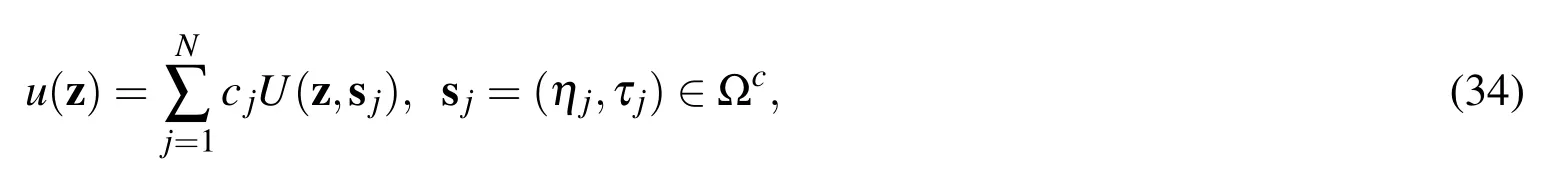
Table 1:Comparing the numerical results for Example 1 with different methods

whereNis the number of source points,cjare unknown coefficients,andsjare source points located in the complement Ωcof Ω =[0,ℓ]× [0,T].For the heat conduction equation we have the basis functions:

It is known that the location of source points in the MFS has a great influence on the accuracy and stability.In a practical application of MFS to solve the BHCP,the source points are uniformly located on two straight lines parallel to thet-axis and not over the final time,which was adopted by Hon and Li(2009)and Liu(2011b),showing a large improvement than the line location of source points below the initial time.After imposing the boundary conditions and the final time condition on Eq.(34)we can obtain a linear equations system:

where

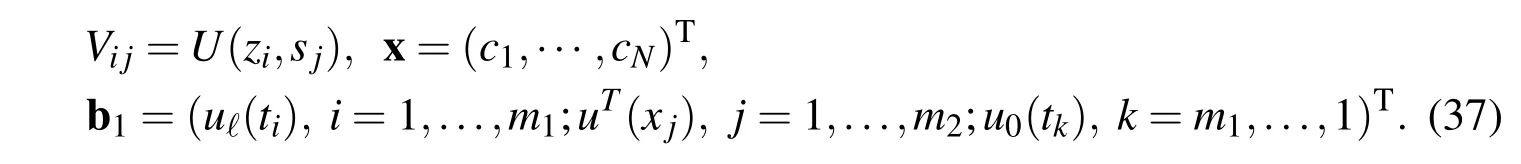
The numbern=2m1+m2of collocation points does not necessarily equal to the numberNof source points.By applying the SMCA to solve the above problem we solve a normal equation:

Since the BHCP is highly ill-posed,the ill-conditioning of the matrix B=VTV in Eq.(38)is serious.To overcome the ill-posedness of Eq.(38)we can employ the SMCA to solve this problem.Here we compare the numerical solution with an exact solution:

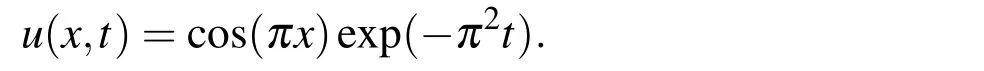
For the case withT=1 the value of final data is in the order of 10-4,which is small in a comparison with the value of the initial temperatureu0(x)=cos(πx)to be retrieved,which isO(1).

We apply the SMCA to solve Eq.(38)withh=0.05 and ε=10-4,and a relative random noise with an intensity σ=10% is added on the final time data.TheSMCA converges with 899 iterations as shown in Fig.5(a),while the sliding quantitysis shown in Fig.5(b).The numerical error as shown in Fig.5(c)by the solid line is smaller than 0.0438.For the purpose of comparison we also apply the RSDM with γ=0.05 to solve this problem;however,over 10000 iterations it does not converge as shown in Fig.5(a)by the dashed line for the residual error.However,the result as shown in Fig.5(c)by the dashed line for numerical error is smaller than 0.05.

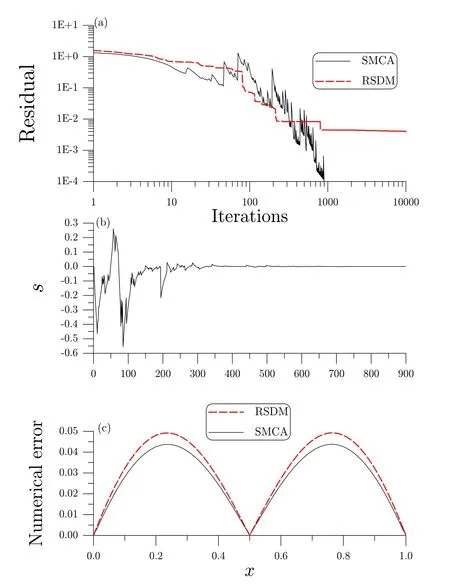
Figure 5:For example 2,(a)comparing the residual errors obtained by RSDM and SMCA,(b)the sliding quantities o SMCA,and(c)comparing the numerical errors.

4.3 Example 3

We solve the Cauchy problem of the Laplace equation under over specified boundary conditions:

whereh(θ)andg(θ)are given functions,and ρ = ρ(θ)is a given contour to describe the boundary shape.The contour in the polar coordinates is specified by Γ ={(r,θ)|r=ρ(θ),0≤ θ ≤2π},which is the boundary of the problem domain

Ω,andndenotes the normal direction.

In the potential theory,it is well known that the method of fundamental solutions(MFS)can be used to solve the Laplace equation when a fundamental solution is known.In the MFS the trial solution ofuat the field point z=(rcosθ,rsinθ)can be expressed as a linear combination of the fundamental solutionsU(z,sj):

wherenis the number of source points,cjare the unknown coefficients,sjare the source points,and Ωcis the complementary set of Ω.For the Laplace equation(39)we have the fundamental solutions:

In the practical application of MFS,frequently the source points are uniformly located on a circle with a radiusR,such that after imposing the boundary conditions(40)and(41)on Eq.(42)we can obtain a linear equations system:

where

in whichn=2m,and

A noise with an intensity σ=10%is imposed on the given data.We fixn=60 and use a circle with a constant radiusR=14 to distribute the source points.By applying the SMCA to solve the normal equation(38)obtained from Eq.(44)we fixh=0.3.Under the convergence criterion ε=10-2,the SMCA converges with 7308 iterations and the residual error is shown in Fig.6(a),while the control force is shown in Fig.6(b)and the sliding quantitysis plotted in Fig.7(a).Along the lower half contourin Fig.6(c)we compare the numerical solution with the exact data given byu=ρ2cos(2θ),π≤θ ＜2π,of which the maximum error is found to be 0.121.

For the purpose of comparison we also apply the OIA/ODV developed by Liu and Atluri(2011a)and the GOIA developed by Liu(2012d)to solve this problem under the same conditions.In Fig.7(b)we compare the relative residuals obtained by these three methods,while in Fig.7(c)we compare the numerical errors,where the maximum error obtained by the SMCA is 0.121,the maximum error by the GOIA is 0.141,and the maximum error by the OIA/ODV is 0.148.Both the GOIA and OIA/ODV do not converge within 10000 iterations under the above convergence criterion ε=10-2.We can say that the performance of SMCA is better than GOIA and OIA/ODV.

4.4 Example 4

In this example we consider an inverse Cauchy problem of the following biharmonic equation:

where Ω is an interior domain in the plane.This inverse Cauchy problem of biharmonic equation is under an incomplete set of data given by

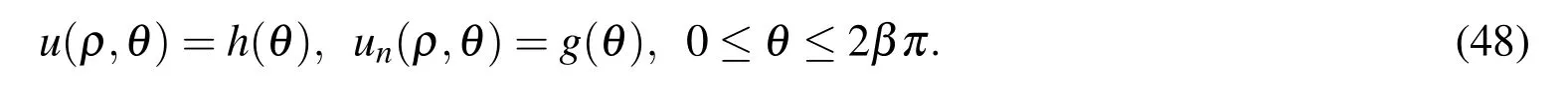
When β =1 we recover to the direct problem.Here we let β ＜ 1 and do not use the overspecified data,such that the present problem is a Cauchy problem with an incomplete set of given data.

For the purpose of comparison we suppose that the exact solution is

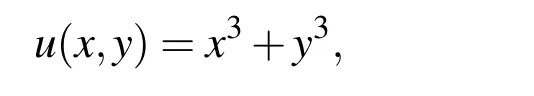
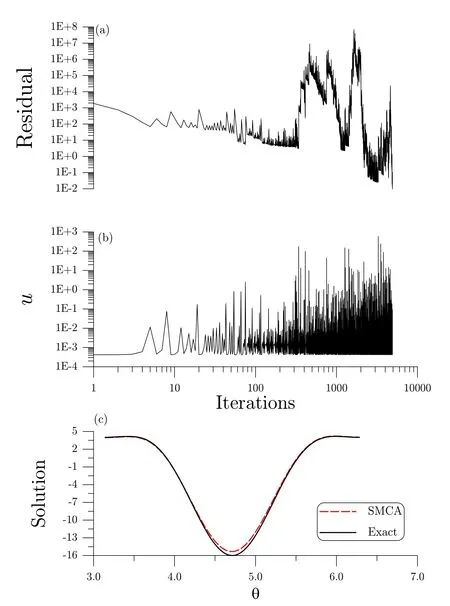
Figure 6:For example 3,(a)the residual error obtained by SMCA,(b)the control force,and(c)comparing the numerical solution with the exact one.

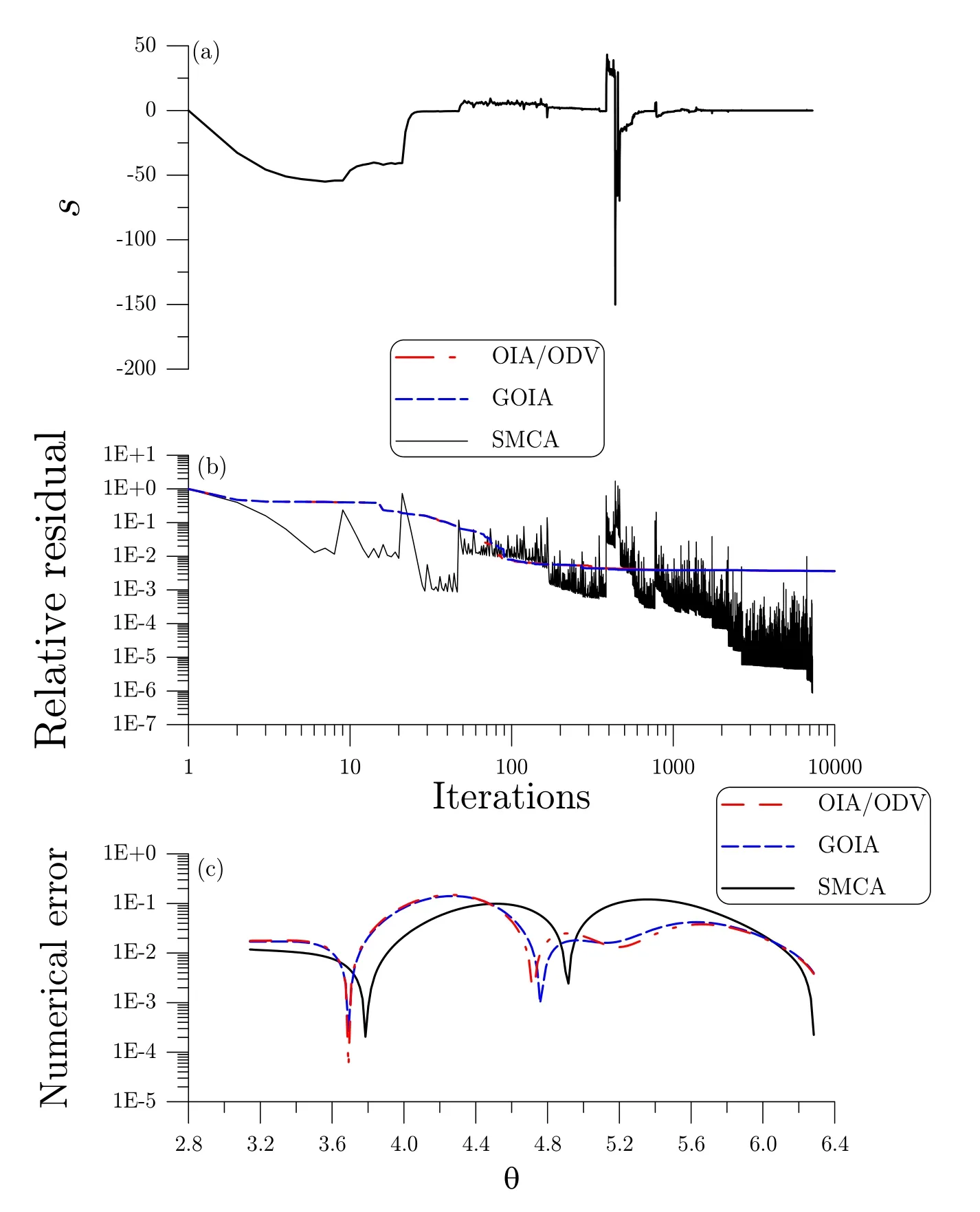
Figure 7:For example 3,(a)the sliding quantity obtained by SMCA,(b)comparing the relative residuals,and(c)comparing the numerical errors.

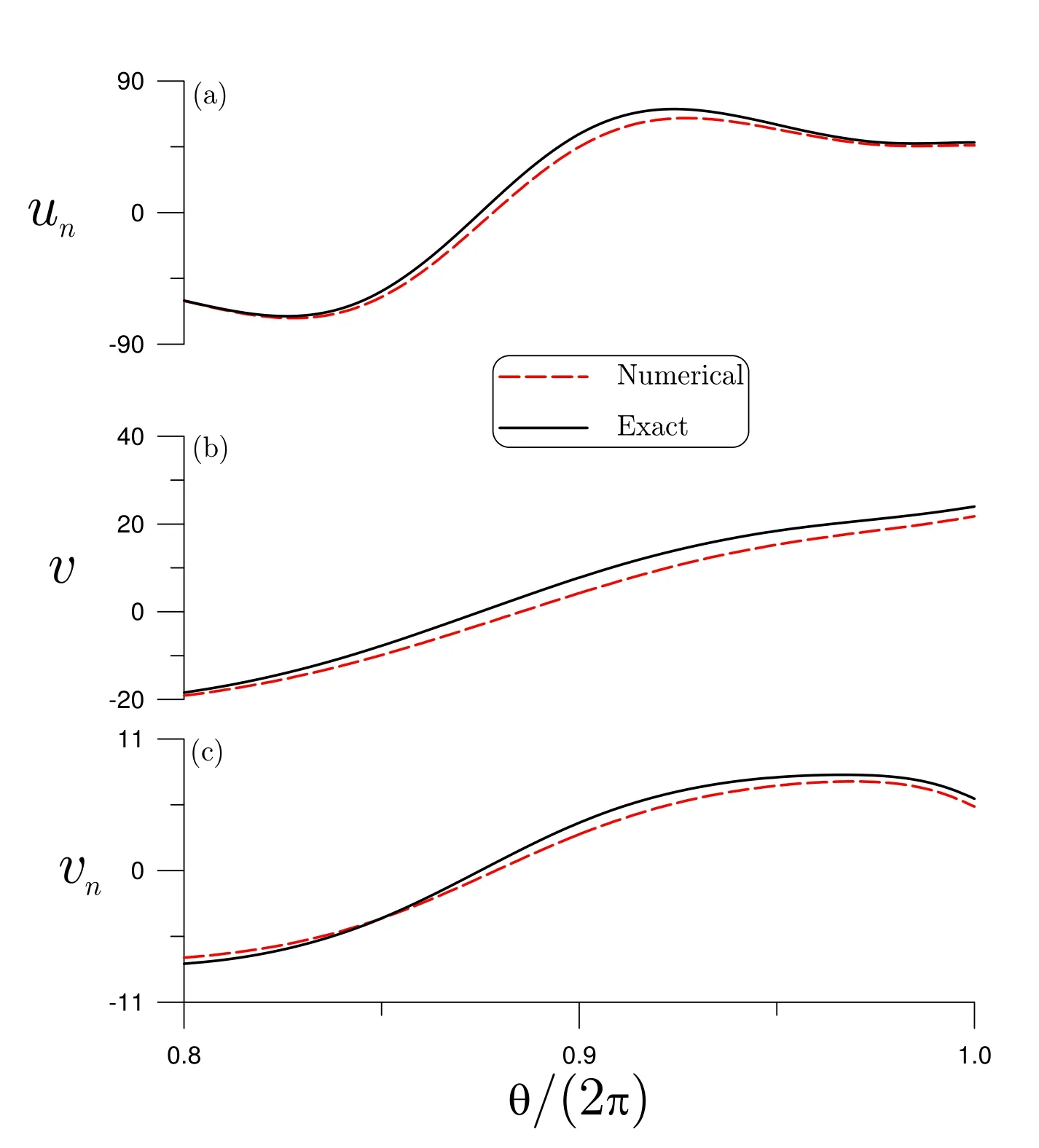
Figure 8:For example 4 of an inverse Cauchy problem of biharmonic equation,comparing the numerical solutions obtained by the SMCA with exact ones.

and the domain is defined by

For this example we apply the following Trefftz method[Liu(2008b)]to solve the inverse Cauchy problem of biharmonic equation:

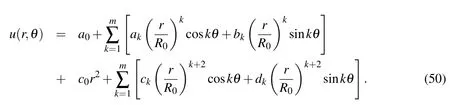
Under the following parametersR0=200,m=20,β =0.8 and σ =0.01 we apply the SMCA to solve this Cauchy problem,of which the results are compared with the exact solutions in Fig.8,wherev=∆u.The results obtained by the SMCA are quite accurate.

5 Conclusions

In orderto tackle the problem of the discrepancy of iteration orbit from the invariant manifold,which causes a slow convergence,in this new invariant-manifold based theory we introduce a sliding mode control method by adding an extra controller with the residual vector as being a gain vector into the evolution equation.The new dynamics is proven to be asymptotically stable towards the zero point of the residual vector,which means that we can quickly find the real solution of a positive linear system by the sliding mode control algorithm(SMCA).In several numerical examples we have observed the sliding behavior with a fast sliding phase,and by comparing with exact solutions,the SMCA can work very effectively for the highly ill-conditioned linear equations system under a large noisy perturbation.We have obtained very accurate solution of the linear Hilbert problem with dimensionn=500,and the number of iterations is still smaller than 100.For the inverse problems the SMCA is also effective,although the noise being imposed on the input data is large up to 10%.

Acknowledgement:Taiwan’s National Science Council project NSC-100-2221-E-002-165-MY3 and the 2011 Outstanding Research Award,granted to the author,are highly appreciated.Acknowledges that the author has been promoted to be a Lifetime Distinguished Professor of National Taiwan University,since 2013.

Absil,P.-A.;Baker,C.G.;Gallivan,K.A.(2007):Trust-region methods on Riemannian manifolds.Found.Comput.Math.,vol.7,pp.303-330.

Adler,R.L.;Dedieu,J.-P.;Margulies,J.Y.;Martens,M.;Shub,M.(2002):Newton’s method on Riemannian manifolds and a geometric model for the human spine.IMA J.Numer.Anal.,vol.22,pp.359-390.

Baker,C.G.;Absil,P.-A.;Gallivan,K.A.(2008):Implicit trust-region methods on Riemannian manifolds.IMA J.Numer.Anal.,vol.28,pp.665-689.

Bhaya,A.;Kaszkurewicz,E.(2006):Control Perspectives on Numerical Algorithms and Matrix Problems.SIAM,Advances in Design and Control 10.

Brown,A.A.;Bartholomew-Biggs,M.C.(1989):Some effective methods for unconstrained optimization based on the solution of systems of ordinary differential equations.J.Optim.Theory Appl.,vol.62,pp.211-224.

Chang,C.W.;Liu,C.-S.(2009):A fictitious time integration method for backward advection-dispersion equation.CMES:Computer Modeling in Engineering&Sciences,vol.51,pp.261-276.

Chehab,J.-P.;Laminie,J.(2005):Differential equations and solution of linear systems.Numer.Algor.,vol.40,pp.103-124.

Chen,C.S.;Cho,H.A.;Golberg,M.A.(2006):Some comments on the ill conditioning of the method of fundamental solutions.Eng.Anal.Bound.Elem.,vol.30,pp.405-410.

Chi,C.C.;Yeih,W.;Liu,C.-S.(2009):A novel method for solving the Cauchy problem of Laplace equation using the fictitious time integration method.CMES:Computer Modeling in Engineering&Sciences,vol.47,pp.167-190.

Eicke,B.;Louis,A.K.;Plato,R.(1990):The instability of some gradient methods for ill-posed problems.Numer.Math.,vol.58,pp.129-134.

Golberg,M.A.;Chen,C.S.(1996):Discrete Projection Methods for Integral Equations.Computational Mechanics Publications,Southampton.

Helmke,U.;Moore,J.B.(1994):Optimization and Dynamical Systems.Springer,Berlin.

Hon,Y.C.;Li,M.(2009):A discrepancy principle for the source points location in using the MFS for solving the BHCP.Int.J.Comput.Meth.,vol.6,pp.181-197.

Ku,C.Y.;Yeih,W.;Liu,C.-S.;Chi,C.C.(2009):Applications of the fictitious time integration method using a new time-like function.CMES:Computer Modeling in Engineering&Sciences,vol.43,pp.173-190.

Liu,C.-S.(2008a):A time-marching algorithm for solving non-linear obstacle problems with the aid of an NCP-function.CMC:Computers,Materials&Continua,vol.8,pp.53-65.

Liu,C.-S.(2008b):A highly accurate MCTM for direct and inverse problems of biharmonic equation in arbitrary plane domains.CMES:Computer Modeling in Engineering&Sciences,vol.30,pp.65-75.

Liu,C.-S.(2009a):A fictitious time integration method for the Burgers equation.CMC:Computers,Materials&Continua,vol.9,pp.229-252.

Liu,C.-S.(2009b):A fictitious time integration method for solving delay ordinary differential equations.CMC:Computers,Materials&Continua,vol.10,pp.97-116.

Liu,C.-S.(2009c):A fictitious time integration method for a quasilinear elliptic boundary value problem,defined in an arbitrary plane domain.CMC:Computers,Materials&Continua,vol.11,pp.15-32.

Liu,C.-S.(2010):The fictitious time integration method to solve the space-and time-fractional Burgers equations.CMC:Computers,Materials&Continua,vol.15,pp.221-240.

Liu,C.-S.(2011a):A revision of relaxed steepest descent method from the dynamics on an invariant manifold.CMES:Computer Modeling in Engineering&Sciences,vol.80,pp.57-86.

Liu,C.-S.(2011b):The method of fundamental solutions for solving the backward heat conduction problem with conditioning by a new post-conditioner.Num.Heat Transfer,B:Fundamentals,vol.60,pp.57-72.

Liu,C.-S.(2012a):Modifications of steepest descent method and conjugate gradient method against noise for ill-posed linear systems.Commun.Numer.Anal.,volume 2012,Article ID cna-00115,24 pages.

Liu,C.-S.(2012b):Optimally scaled vector regularization method to solve illposed linear problems.Appl.Math.Comp.,vol.218,pp.10602-10616.

Liu,C.-S.(2012c):The concept of best vector used to solve ill-posed linear inverse problems.CMES:Computer Modeling in Engineering&Sciences,vol.83,pp.499-525.

Liu,C.-S.(2012d):A globally optimal iterative algorithm to solve an ill-posed linear system.CMES:Computer Modeling in Engineering&Sciences,vol.84,pp.383-403.

Liu,C.-S.(2012e):Optimally generalized regularization methods for solving linear inverse problems.CMC:Computers,Materials&Continua,vol.29,pp.103-127.

Liu,C.-S.(2013a):An optimal tri-vector iterative algorithm for solving ill-posed linear inverse problems.Inv.Prob.Sci.Eng.,vol.21,pp.650-681.

Liu,C.-S.(2013b):A dynamical Tikhonov regularization for solving ill-posed linear algebraic systems.Acta Appl.Math.,vol.123,pp.285-307.

Liu,C.-S.(2014a):A globally optimal tri-vector method to solve an ill-posed linear system.J.Comp.Appl.Math.,vol.260,pp.18-35.

Liu,C.-S.(2014b):A new sliding control strategy for nonlinear system solved by the Lie-group differential algebraic equation method.Commun.Nonlinear Sci.Numer.Simulat.,vol.19,pp.2012-2038.

Liu,C.-S.;Atluri,S.N.(2008):A novel time integration method for solving a large system of non-linear algebraic equations.CMES:Computer Modeling in Engineering&Sciences,vol.31,pp.71-83.

Liu,C.-S.;Atluri,S.N.(2009a):A Fictitious time integration method for the numerical solution of the Fredholm integral equation and for numerical differentiation of noisy data,and its relation to the filter theory.CMES:Computer Modeling in Engineering&Sciences,vol.41,pp.243-261.

Liu,C.-S.;Atluri,S.N.(2009b):A highly accurate technique for interpolations using very high-order polynomials,and its applications to some ill-posed linear problems.CMES:Computer Modeling in Engineering&Sciences,vol.43,pp.253-276.

Liu,C.-S.;Atluri,S.N.(2011a):An iterative method using an optimal descent vector,for solving an ill-conditioned systemBx=b,better and faster than the conjugate gradient method.CMES:Computer Modeling in Engineering&Sciences,vol.80,pp.275-298.

Liu,C.-S.;Atluri,S.N.(2011b):An iterative algorithm for solving a system of nonlinear algebraic equations,F(x)=0,using the system of ODEs with an optimum α in˙x=λ[αF+(1-α)BTF];Bij=∂Fi/∂xj.CMES:Computer Modeling in Engineering&Sciences,vol.73,pp.395-431.

Liu,C.-S.;Atluri,S.N.(2011c):Simple"residual-norm"based algorithms,for the solution of a large system of non-linear algebraic equations,which converge faster than the Newton’s method.CMES:Computer Modeling in Engineering&Sciences,vol.71,pp.279-304.

Liu,C.-S.;Chang,C.W.(2009):Novel methods for solving severely ill-posed linear equations system.J.Marine Sci.Tech.,vol.17,pp.216-227.

Liu,C.-S.;Hong,H.K.;Atluri,S.N.(2010):Novel algorithms based on the conjugate gradient method for inverting ill-conditioned matrices,and a new regularization method to solve ill-posed linear systems.CMES:Computer Modeling in Engineering&Sciences,vol.60,pp.279-308.

Liu,C.-S.;Yeih,W.;Atluri,S.N.(2009):On solving the ill-conditioned systemAx=b:general-purpose conditioners obtained from the boundary-collocation solution of the Laplace equation,using Trefftz expansions with multiple length scales.CMES:Computer Modeling in Engineering&Sciences,vol.44,pp.281-311.

Smith,S.T.(1994):Optimization techniques on Riemannian manifolds:Hamiltonian and gradient flows,algorithms and control.Fields Inst.Commun.,vol.3,pp.113-136.

Tikhonov,A.N.;Arsenin,V.Y.(1977):Solutions of Ill-Posed Problems.John-Wiley&Sons,New York.

Utkin,V.I.(1978):Sliding Modes and Their Application in Variable Structure Systems.Mir Publishers,Moscow.

Utkin,V.I.(1992):Sliding Modes in Control and Optimization.Springer-Verlag,New York.

Yang,Y.(2007):Globally convergent optimization algorithms on Riemannian manifolds:Uniform framework for unconstrained and constrained optimization.J.Optim.Theory Appl.,vol.132,pp.245-265.