Construction of an Edge Finite Element Space and a Contribution to the Mesh Selection in the Approximation of the Second Order Time Harmonic Maxwell System

J.E.Sebold,L.A.Lacerda and J.A.M.Carrer

1 Introduction

In a numerical formulation,if one needs to directly represent a vector quantity in a discretized form,the alternative when using nodal basis functions is the separate treatment of each component of the vector field,which individually reduces to scalar functions.

Arises from this fact a dificulty related with the continuity of the discretized vector quantity across adjacent elements in the finite element mesh.For instance,in a common side of adjacent elements,nodes are shared and since the approximation is performed component by component,this approach results in continuity of all components of the vector quantity across the elements.However,if each element belongs to a different material domain,the imposed continuity produces a fisically incorrect solution.Such solutions are obtained since the nodal basis functions approach do not guarantee the continuity of the interpolation function derivatives between adjacent elements.

Along time,novel approaches were conceived to overcome this problem.Among them,one may highlight the development of techniques characterized by the use of another variety of finite elements as an alternative to the original nodal approach.Such alternatives were introduced in the works of Whitney(1957)and Nédélec(1980).

Despite using edge vectors sets in a completely different context to the finite element method developed in this work,Whitney pioneered the use of polynomials vector space to generate such sets Monk(2003b).These edge vectors or zero order elements in the context of the finite element method are an approximation by function with constant tangential components at the element edges.Such type of elements are commonly referred in the literature as Whitney elements.

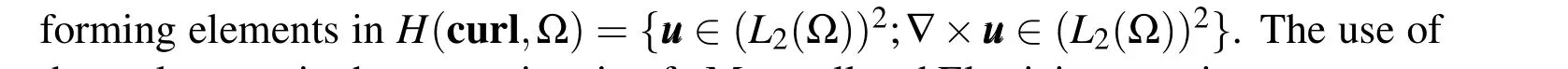
The Sobolev spacesH(curl,Ω)play a central role in the variational theory of Maxwell’s equations since,according to Monk(2003b)this space corresponds to the space of finite energy solutions.In this sense,it can be guaranteed the existence,uniqueness and regularity of physically significant discrete solutions Greenleaf et al.(2007).Thus,it is convenient to take this finite element space to retrieve a subspace class of suitable finite elements for the Maxwell’s equations system.

Anotherfeature ofthisspace isthe choice ofthe finite elementdiscretization,which is necessary for the continuity of the tangential components of the field E across adjacent elements.Moreover,there is no obligation for the normal vector components being continuous.

Another relevant issue is the dispersion relation for the edge finite elements.Several authors have considered the dispersive behaviour of the finite element method.Christon(1999)considered the dispersive behaviour of a variety of finite element methods for the wave equation,presenting numerical comparisons of the discrete phase and group velocities with exact values.Monk and Parrot(1994)considered the dispersive behaviour of fisrt order triangular finite elements for Maxwell’s equations,while refining meshes.Monk and Cohen(1998)conducted a dispersion analysis for Nédélec type elements for time dependent Maxwell’s equations using a mass matrix lumping on tensor products in two and three dimensional meshes.Ihlenburg and Babuška(1997)studied the dispersive properties of higher order finite elements for the Helmholtz equation in one dimension,obtaining estimates for the approximation to the fifth order in whichωh＜1.Numerical evidences led to the conjecture that elements of orderpprovide an approximation of order 2pin dispersion relation when the mesh size parameterhtends to zero.Monk(2003a)showed proof of convergence of the Nédélec finite elements applied to a cavity problem with Maxwell’s equations.The cavity was assumed to be a Lipschitz polyhedron,modelled with a rectangular non-uniform mesh.Ainsworth(2003)demonstrated that the numerical dispersion relation displays three different behaviours depending on the order of the method in relation to the mesh parameter and to the wave number.These behaviours are described as:Oscillation Phase,Transition Zone and Super-Exponential Decay.Ainsworth and Coyle(2001)studied a hierarchical basis functions set for the Galerkin discretization ofH(curl,Ω)space for both hybrid meshes containing quadrilaterals and triangles with a non-uniform arbitrary polynomial order.

In this work,it is shown a second order time-harmonic Maxwell system problem with its approximation with edge finite elements.From the numerical results a dispersion relation analysis is performed using the numerical phase velocity,allowing the selection of an edge size parameter for a uniform quadratic elements mesh.

2 Surface Differential Operators

2.1　Surface Cross Product

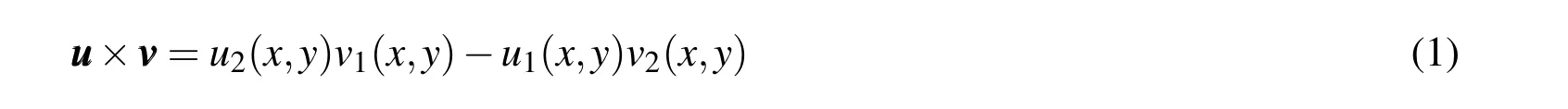
2.2　Surface Gradient

LetSbe a surface with smooth boundary and unit normal vectorn n n.For a scalar functionφ∈H1(S)the surface gradient∇Sφ∈L2t(S)is defined as:

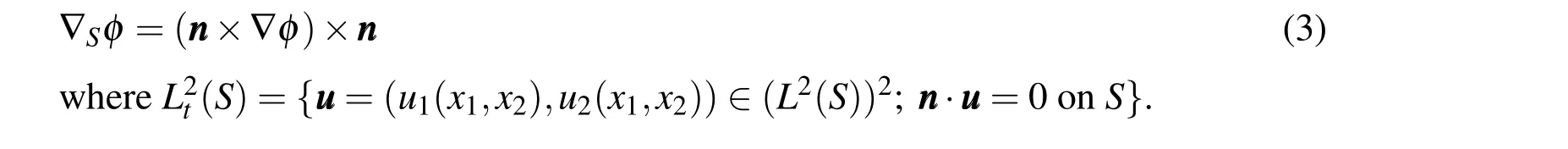
2.3　Surface Scalar Rotational

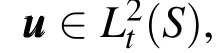
2.4　Surface Vector Rotational

IfSdenotes a Lipschitz domain in the planexy,Reddy(1986),then for a given scalar functionφ=φ(x,y),defined onS,one can denote and define the suface vector rotational,respectively,by:

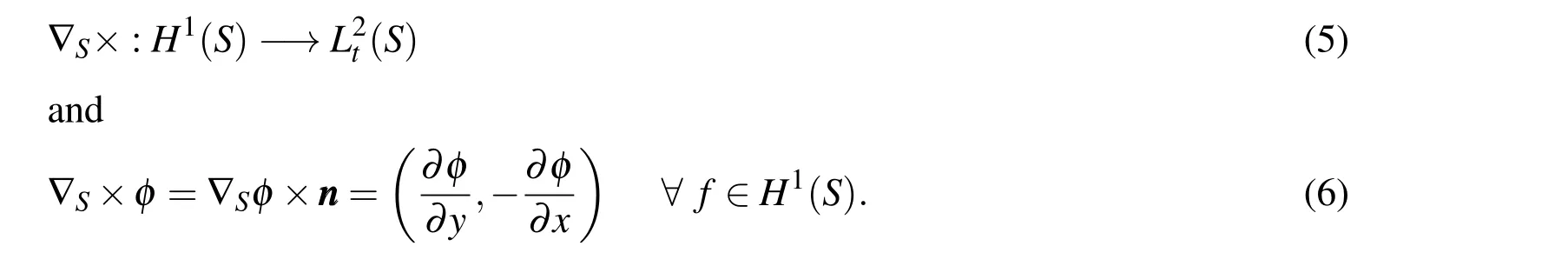
Note that equation(6)is nothing more than the product between the rotation matrix and theφgradient.

2.5　Surface Divergence

One can denote the surface divergence by the operator∇S·:L2t(S)−→H1(S)′and define it as

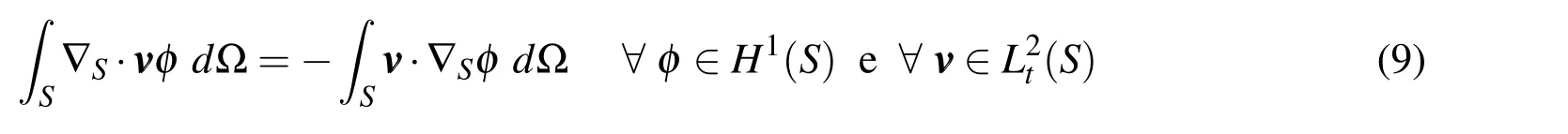
The Finite Element Method is based on the variational formulation or weak formulation of boundary value problems.Thus,the following theorem is very useful in the variational formulation of the second order time harmonic Maxwell system,which will be discussed below.

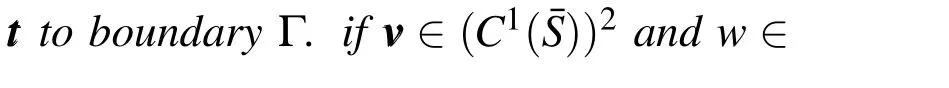
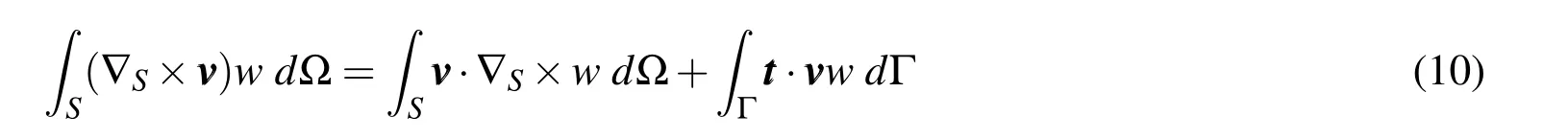
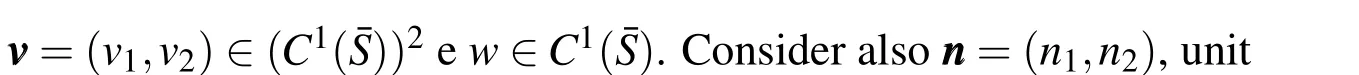
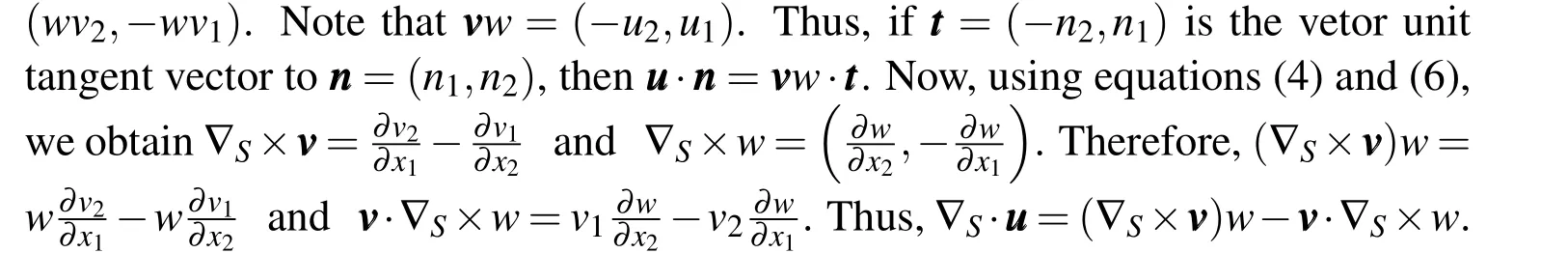
3 Second Order Time Harmonic Maxwell System

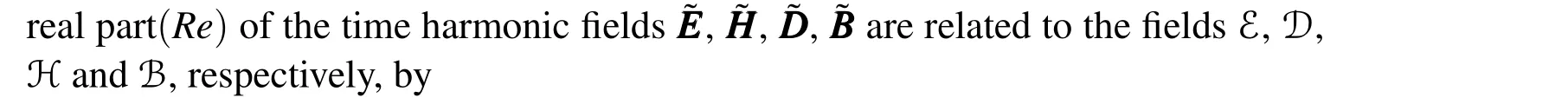
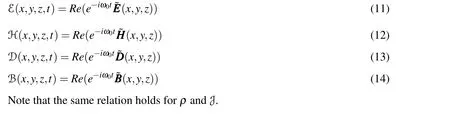
Lemma 3.1:If Re(A1e−iω0t)=Re(A2e−iω0t)for all t,then A1=A2.

Proof:SupposeA1/=A2.Consider thatA1=a+biandA2=c+di,wherea,b,c,d∈R.By hypotesisRe(A1e−iω0t)=Re(A2e−iω0t)for allt,thus fort=0,one hasRe(A1)=Re(A2).Consider nowt=π/2ω0,so one hasIm(A1)=Im(A2)(imaginaries parts),which contradicts the choiceA1/=A2.Therefore,A1=A2.

Likewise,similar conclusions can be found for the other equations(I1.a),Jackson(1999).So,the time harmonic Maxwell system can be written

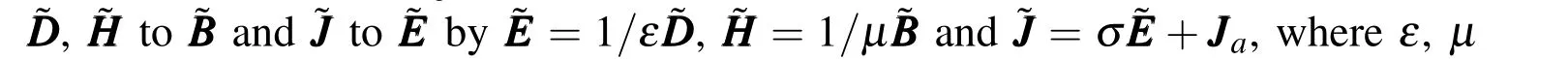
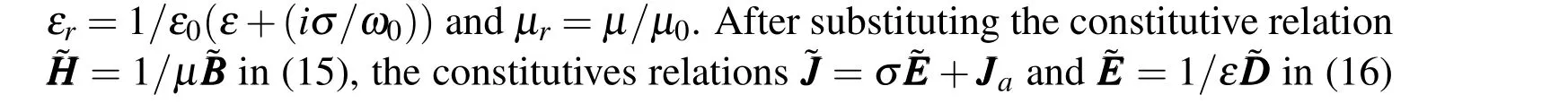
and using(19),the first order time harmonic Maxwell system obtained;it is written as:

4 Description of Edge Finite Elements Space

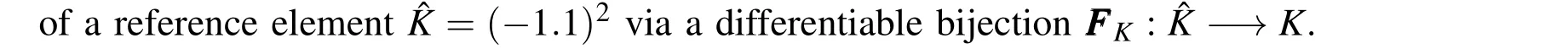
4.1　Degree of Freedom

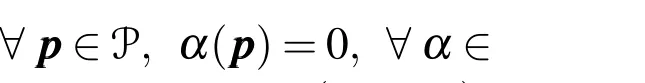
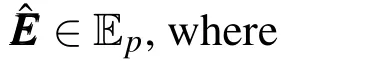
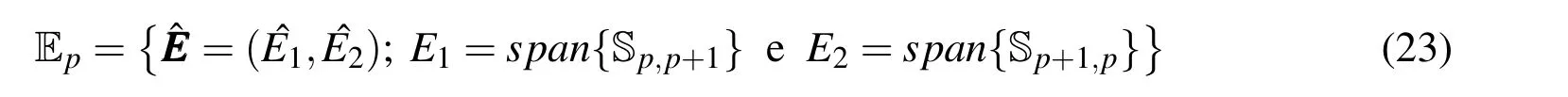
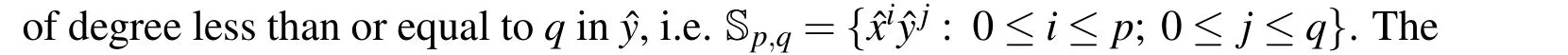
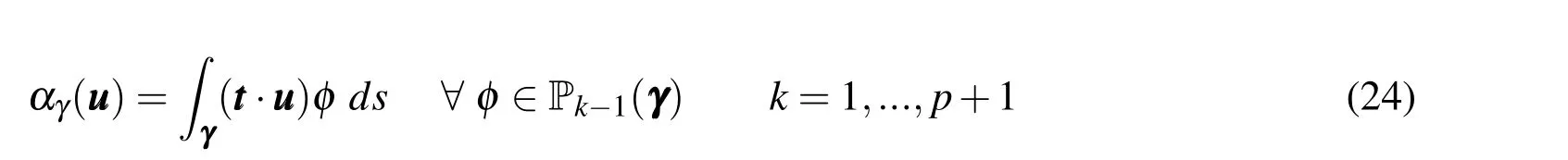
whereφ1∈Sk−2,k−1andφ2∈Sk−1,k−2.One has a total of 2p(p+1)degrees of freedom within the reference elementˆK.

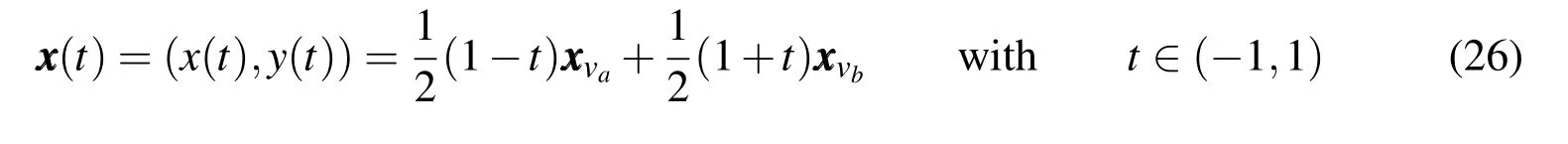
Hence,according to Kaplan(1970),one has

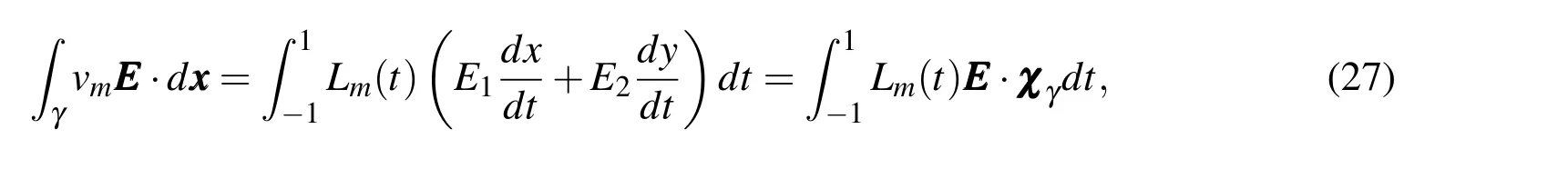
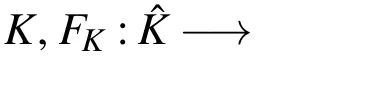
whereJKis an invertible square matrix andb b bis a translation vector.Note thatFKis a differentiable bijection,and that the Jacobian matrix transformation is given bydFK=JK.It comes from the covariant transformation,Kaplan(1970),that the tangent vectorsχandτare related by

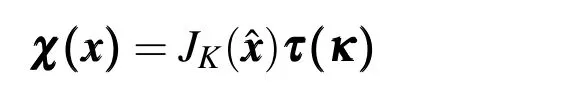
Therefore,equation(27)can be represent by:

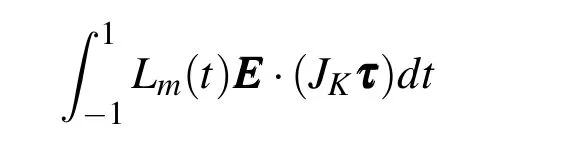
By using the mappingFγ,restricted to reference edgeγand withm=k,one has

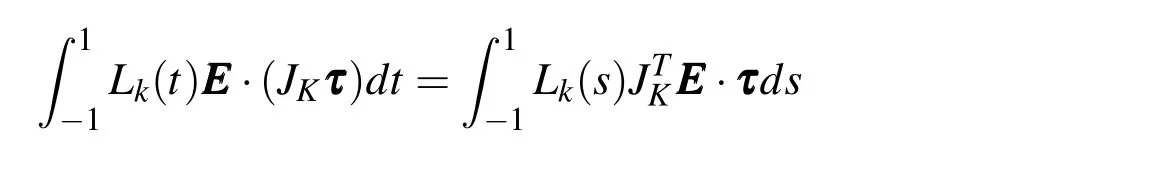
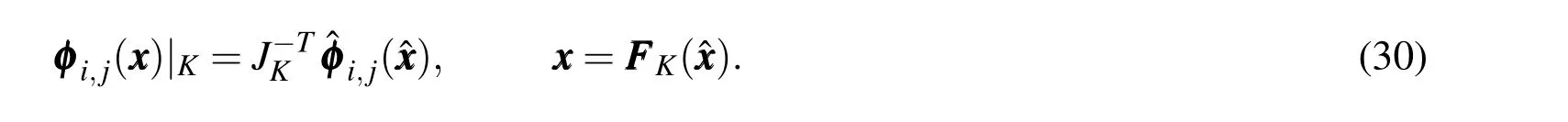
The degreesoffreedom on the edgesensuresthat(K,P,Σ)isH(curl,Ω)-conforming;complementing them with the degrees of freedom inside of element,it is ensured that(K,P,Σ)is unisolvente(see Theorem 5 of Nédélec(1986)).

4.2　Hierarchical Basis Functions

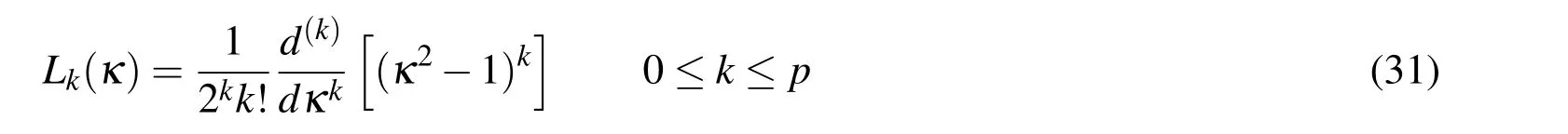
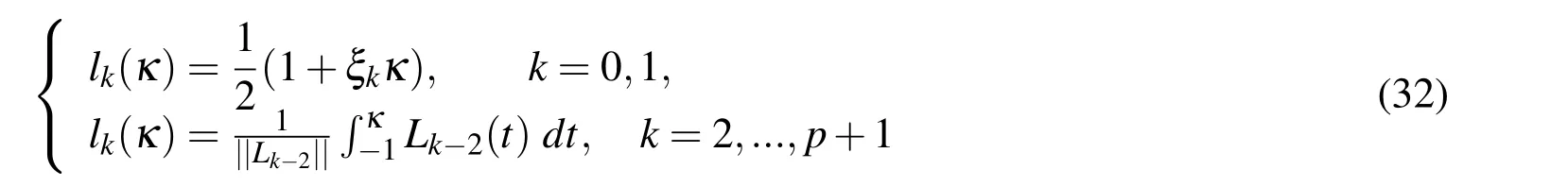
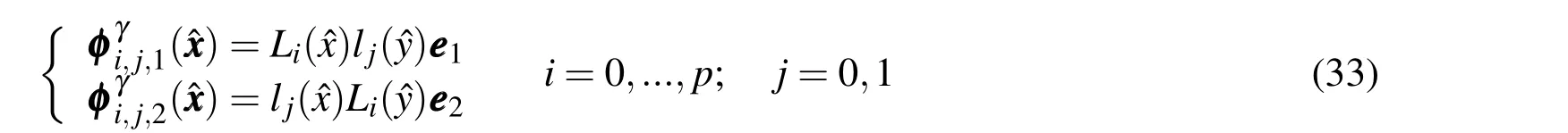
Inspite of the representations(33)and(34)be well simplified,a notation to differentiate the"edges functions"were used.This classification takes into account the edges of a quadrilateral reference element:

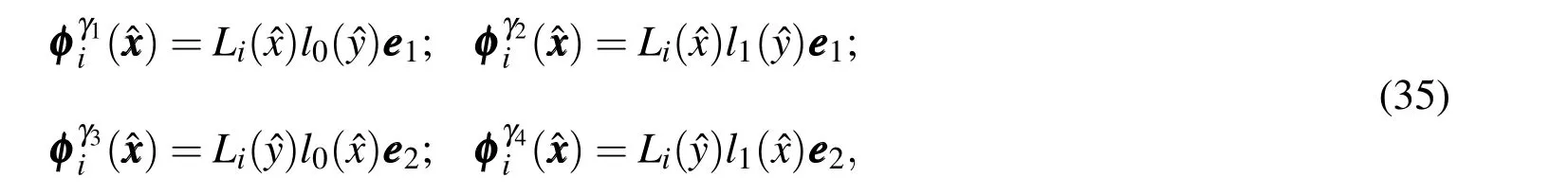
Thus,the basis function associated with the edges satisfy

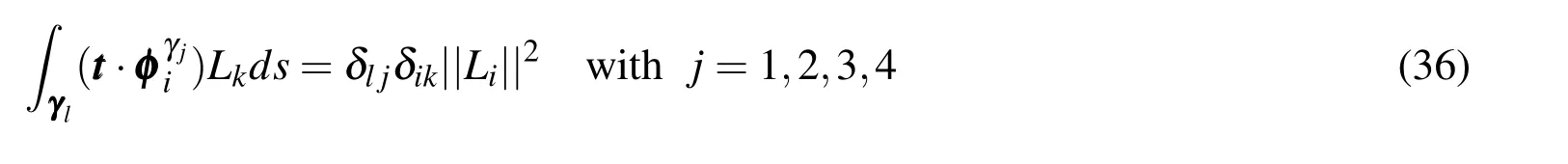
whereδis the Kronecker delta.Similarly,the basis functions associated to the inside of an element satisfies

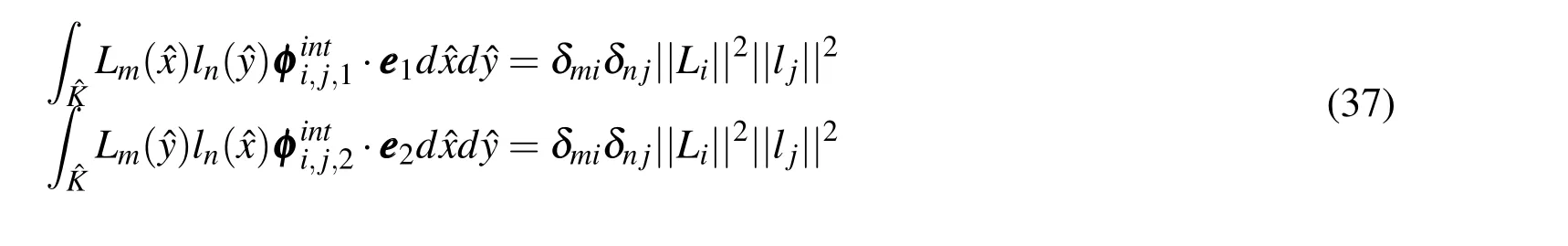
4.3　Basis Function for Whitney Elements(p=0)

An emphasis on the definition of Epfor the casep=0,implies S0,1={1,ˆy}and S1,0={1,ˆx};therefore:

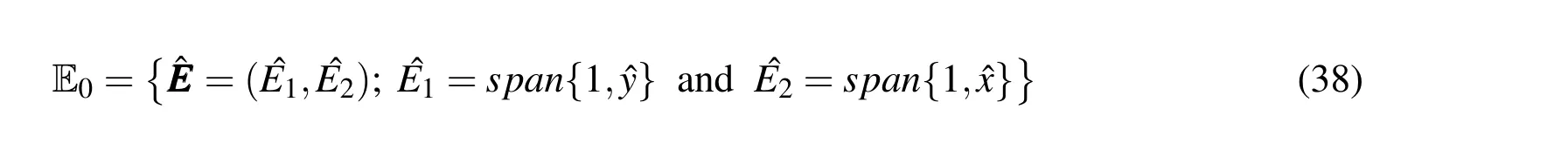
For Whitney elements each edge presents only one degree of freedom(see equation(24)),thus we can define the basis functions can be defined as:

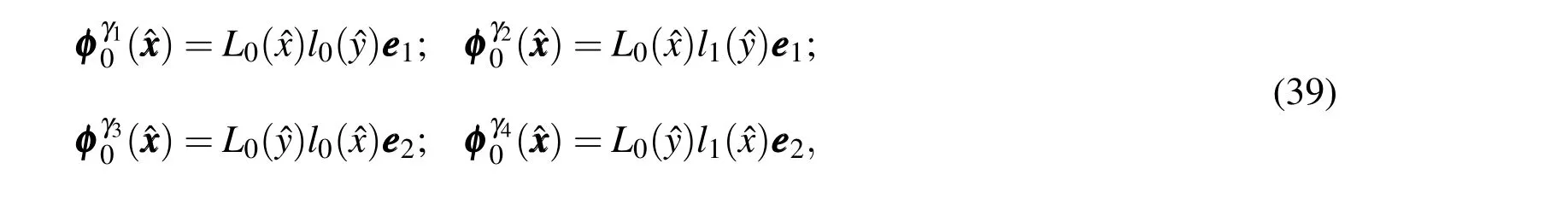
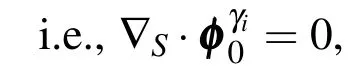
4.4　Basis Function for Nédélec Elements(p=1)

The space of polynomials associated with the Nédélec elements of orderp=1 on the reference elementˆKis defined as

and E1is constructed by increasing the space E0–Hierarchical basis.Furthermore,we note that there are four new basis functions on edges that are generated by the elementsˆx,ˆxˆy∈S1,2andˆy,ˆyˆx∈S2,1,which will be added to the edges together with the basis functions for elements of Whitney.

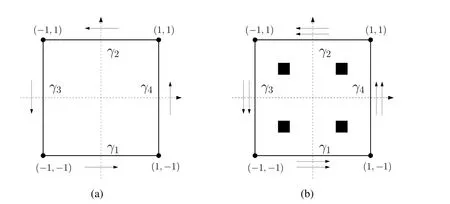
Figure 1:(a)Degrees of freedom for Whitney elements.The arrows indicate the zero-order moment of the tangential fieldˆE E E.Note that the direction of the tangent remains in the anti-clockwise around the element;(b)The arrows indicate the degrees of freedom of the elements of order p=1 distributed on the edges.The black squares in the interior of the element represent the degrees of freedom necessary for a quadrilateral.

Note that,the elements of orderp=1 are provided degrees of freedom on the edges and inside the element.Thus,the basic functions of these elements are organized as follows:

1.Basis function in the edges:

Note that the first four basis functions of the edge are the same basic functions for elements of orderp=0.The basis functions in(42)are built using the weight functionvk=Lk,satisfying(36).

Basis functions in(43)are constructed in order to satisfy(37).

5 Numerical Tests

Now,in order to illustrate the performance of Whitney-Nédélec edge finite elements,the problem of the propagation of a plane wave through of a square domainΩ =(0,1)2with boundary Γ is analysed.Suppose Ω in the vacuum,thusε=ε0andµ=µ0.

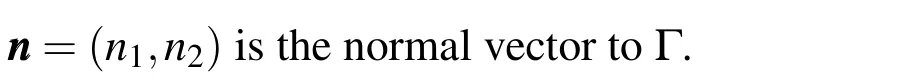
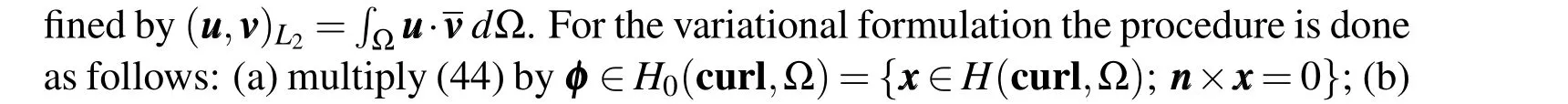
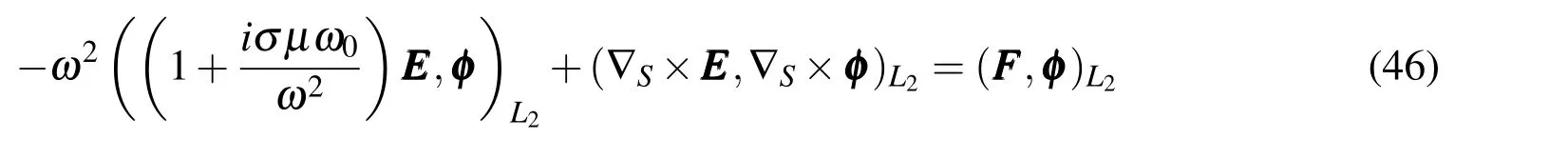
will not be coercive,Monk(1991).To avoid this problem,the use of Fredholm theory to provides the conditions that will ensure the existence and uniqueness of a solution,Monk(2003b).Consequently,for any value imposed toσa solution to(46)can be find.

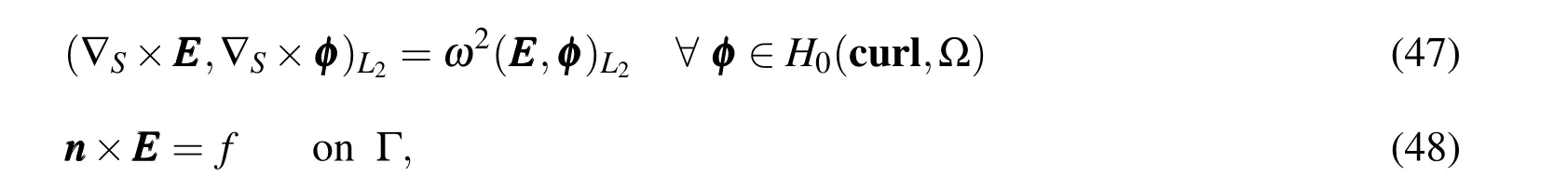
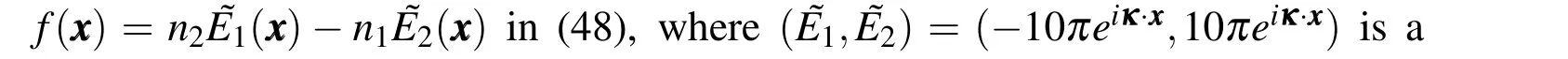
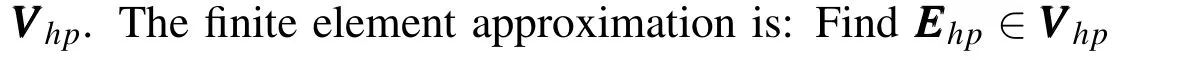
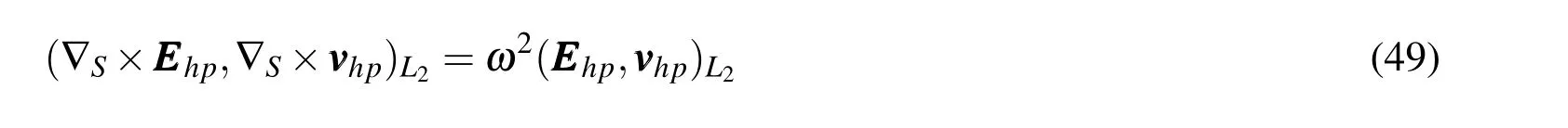
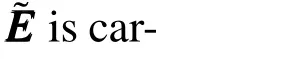
6 Mesh parameter selection

In the preceedings section it could be seen that the error of approximation by finite elements may cause a phase difference and a amplitude difference with respect to the exactsolution,see Figure 4(b).Thiseffectdependsnotonly on the mesh parameterh,but also on the temporal frequencyω,see Figures 5(a)and 5(b).This factcan be analyzed through the study of the dispersive properties of numerical solution for homegeneous scalar Helmholtz equation in an infinity mesh,Ainsworth(2003).Aiming to find an expression for the discrete dispersion relation for Whitney and N�d�lec Elements,one can consider some relations between the Helmholtz equation and the equation(44),withσ=0,i.e.,

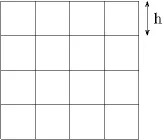
Figure 2:Example particular mesh used in the numerical experiments,with n2=16,being n the number of elements in the base domain,i.e.h=1/n.

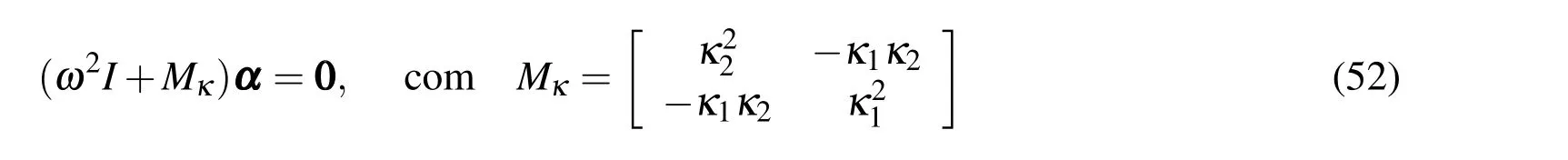
Consideringdet(ω2I+Mκ)=0,the following relation arises

Equation(53)is the dispersion relation for(51).According to the next lemma solutions to the equation(51)can be obtained from solutions to scalar homogeneous Helmholtz equation.

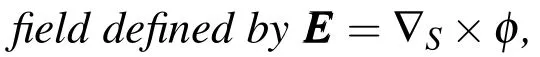
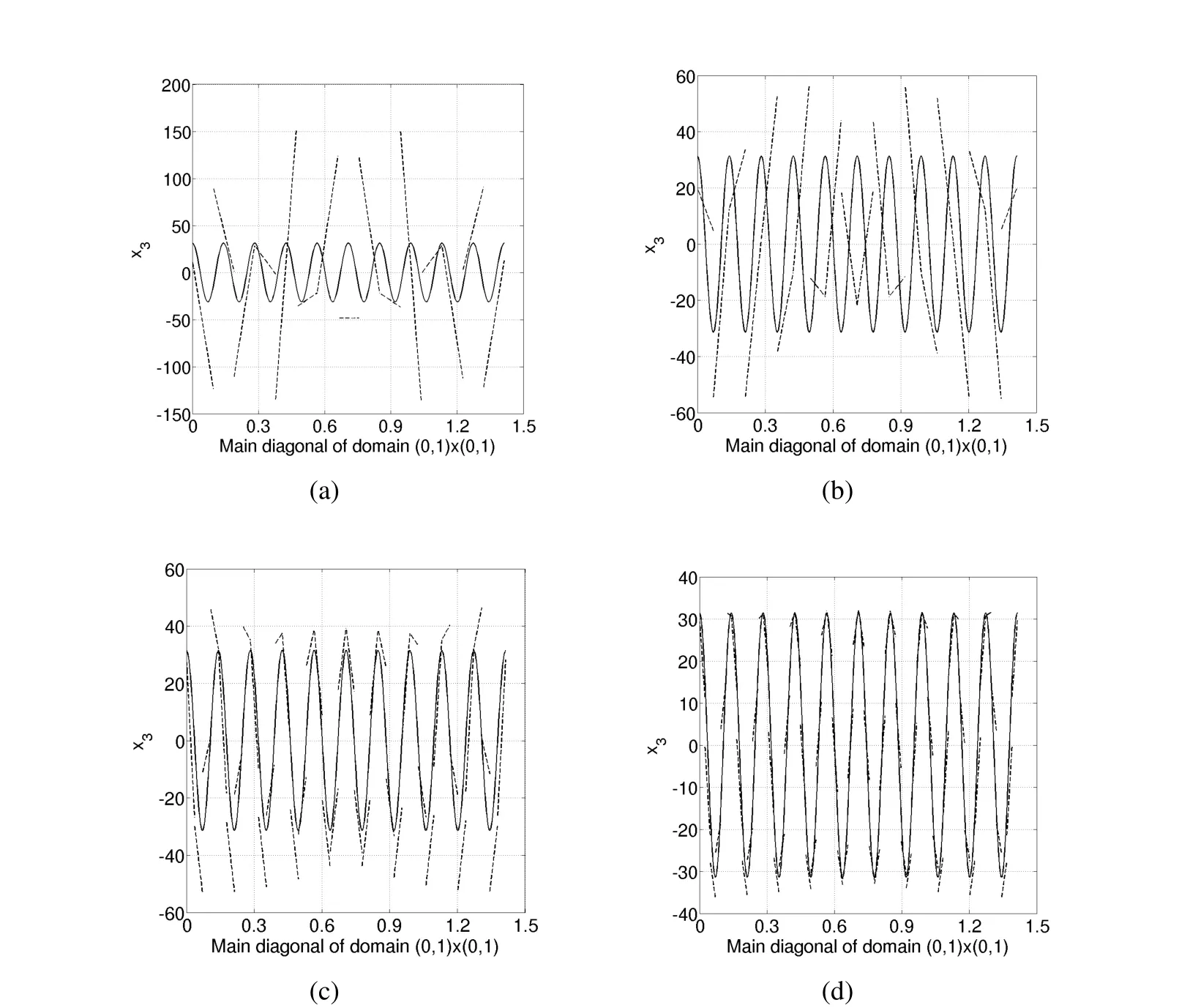
Figure 3:Variation along the main diagonal of the exact solution(continuous line)and of the numerical solution(dashed line)using Whitney elements in the levels:(a)h=1/15;(b)h=1/20;(c)h=1/40;(d)h=1/60.

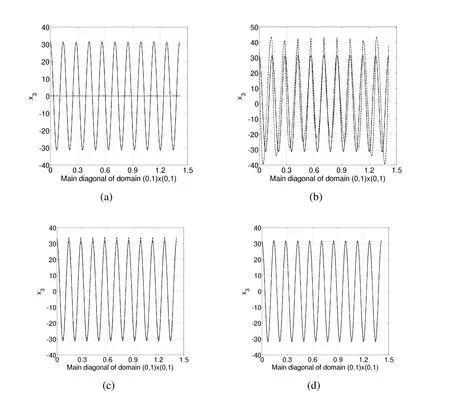
Figure 4:Variation along the main diagonal of the exact solution(continuous line)and of the numerical solution(dashed line)using first order Nédélec elements in the levels:(a)h=1/5;(b)h=1/10;(c)h=1/30;(d)h=1/60

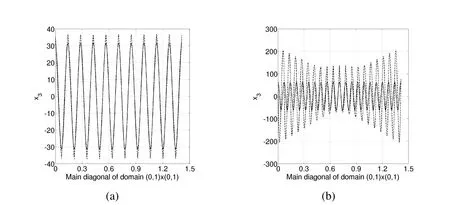
Figure 5:(a)Variation along the main diagonal(h=1/20)of the exact solution(continuous line)and of the numerical solution with first order Nédélec elements of the first order(dashed line)with ω2=200π2 and with(b)ω2=800π2.

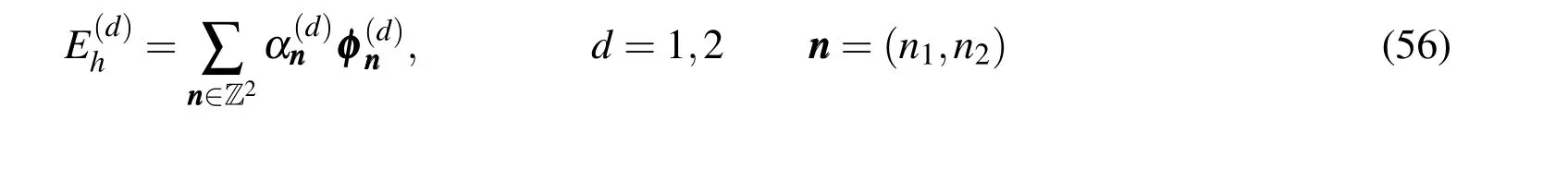
where Z is the integer set and

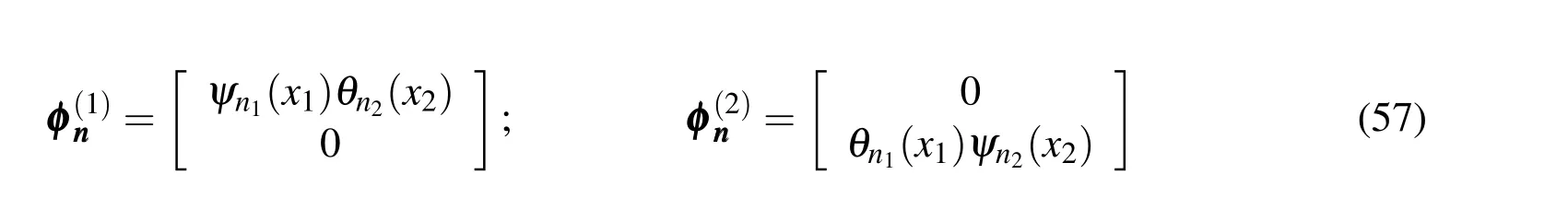
It is noteworthy that the basis functions used in this section are different from the basic functions used in Section 4.The reason for this change is that theθnfunctions are interpolants simplifying and so facilitate the dispersion analysis.However,the spaces generated by the two basis is the same.

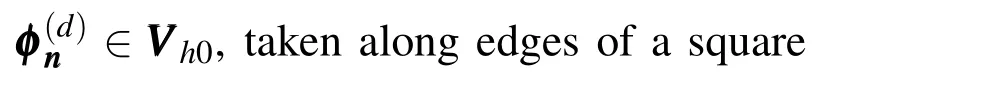
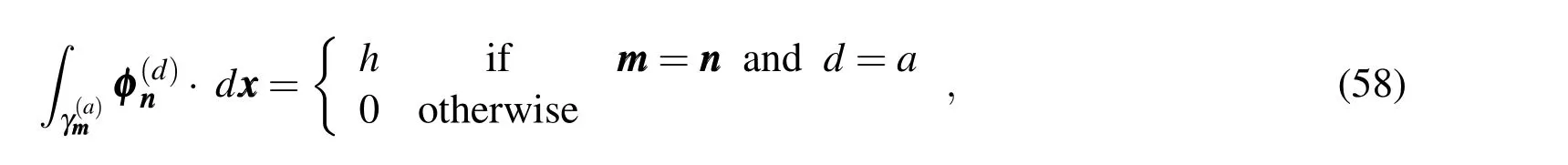
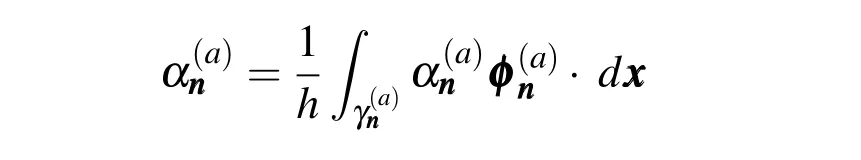
Using equation(56)in thedthspatial component,the following expression arises:

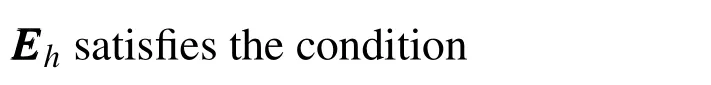
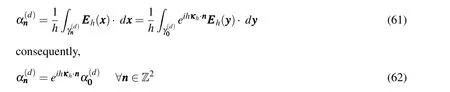
Replacing equation(62)in(56),one finds

and thus,decoupling the sum for each component ofn n n,it follows that

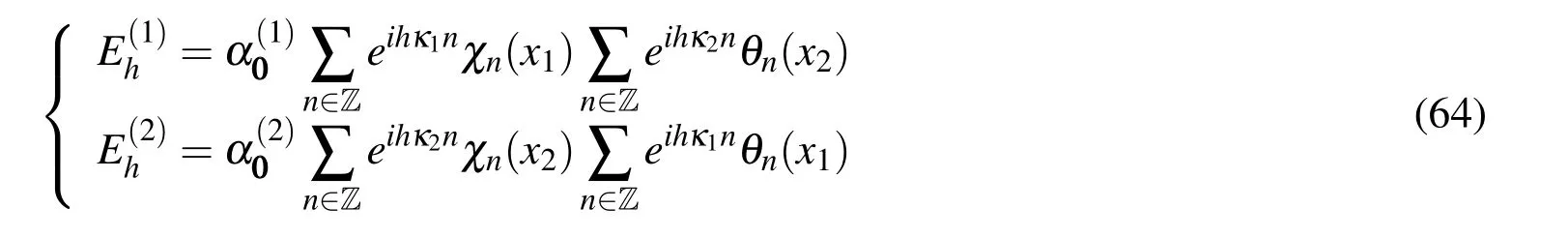
It follows from(60)that

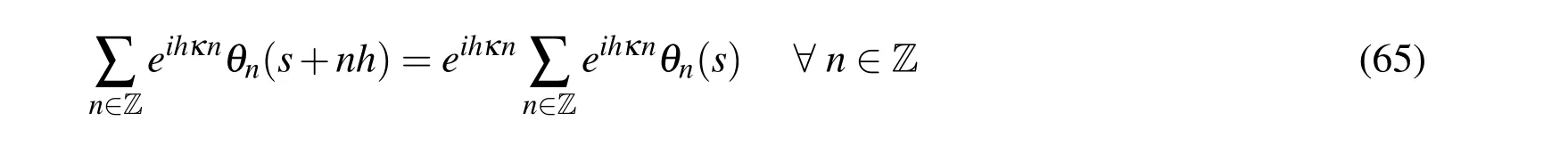
Letu∈H1(Ω)be an analytic solution of the homogeneous scalar Helmholtz equation in one dimension,defined byu(s)=eiκs.ConsiderVha finite element space.Note that equation(65)can be seen as a discrete version ofu,i.e.,

Hence,the following variational problem can be considered:Finduh∈Vhsuch that

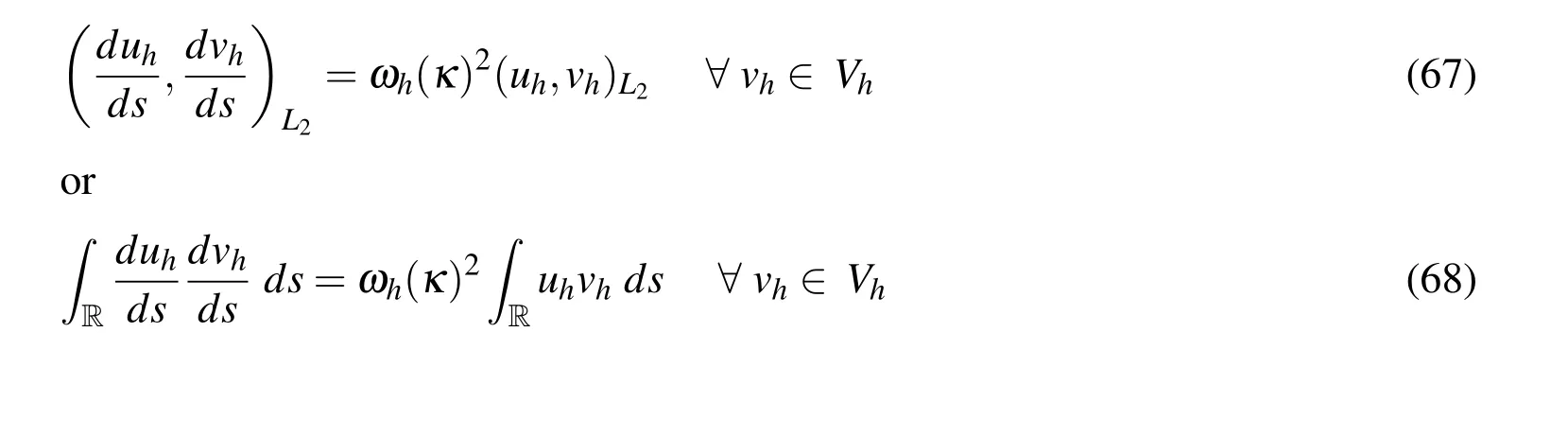
whereωh(κ)2can be calculated by replacing(66)in(68),by definingvh=θm,withm∈Z,and by noting thatθn(s)θm(s)/=0 just whens∈(mh−h;mh+h).By taking the integral in each of the three plots(n=mh−h,mh,mh+h),one has

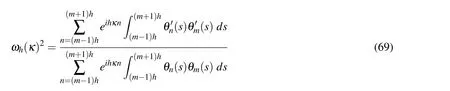
After solving the integrals and using the identity 2cos(κh)=eihκ+e−ihκ,the following expression arises:

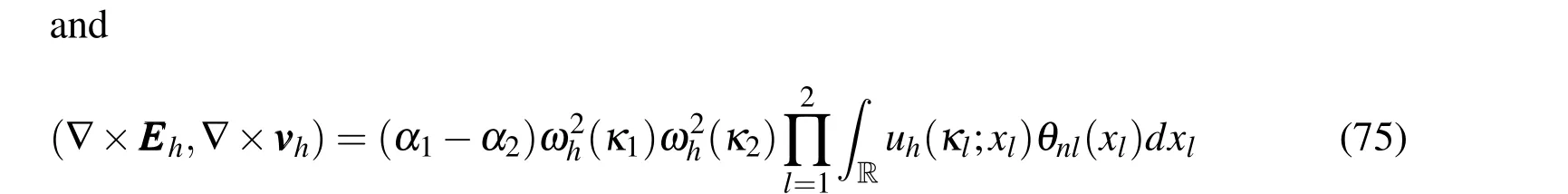
Thus,equation(49)simplifies to the algebraic equation

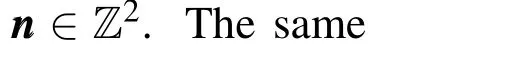
Expression(78)is the discrete dispersion relation corresponding to the Whitney elements.By following the same steps,and making appropriate considerations to the degreepof the interpolation functions,an expression for the general case can be found;it reads:

Using linear interpolants(p=0 order in the case of Whitney elements)in the discretization of the homogeneous Helmholtz equation,Babuška and Ihlenburg(1995),Thompson and Pinsky(1994)and Ainsworth(2003)demonstrated the following expression for relation discrete dispersion

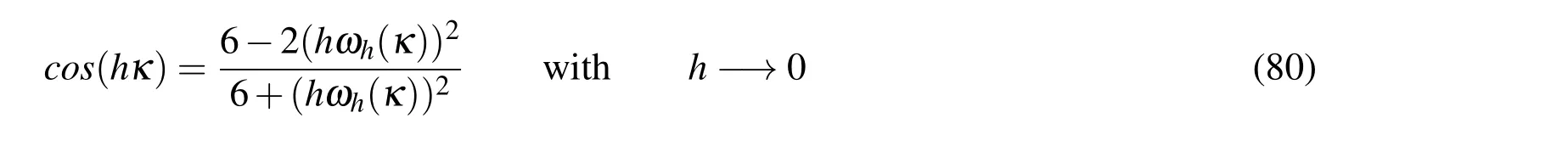
which isthe same equation(70),written in terms ofωh(κ).Theorem 1 in Ainsworth(2003),showshow to build rationalexpressions forthe cosine through Padéapproximation,which are related to the orderq=p+1 of the finite element method for the approximation of the Helmholtz equation.Such rational functions demonstrate better accuracy with the growth of theq-order used in interpolants of the discretized solution.In particular,forp=1(first-order Nédélec elements),the cosine rational expression is:

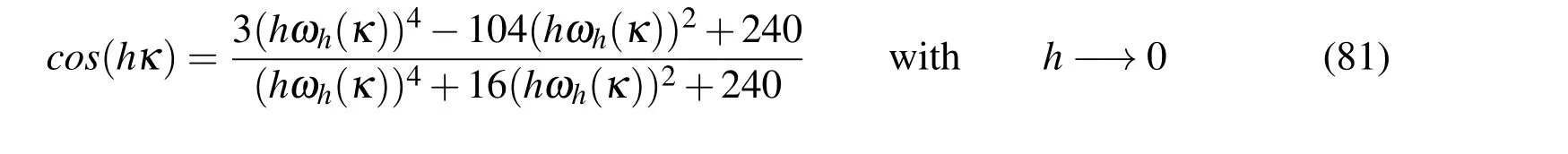
The purpose of this section is to show how to select a mesh parameterh,which will make the difference in phase velocity,between the exact and approximate solution of the problem(47)-(48),become negligible.With this purpose,consider that the numerical phase velocityCis defined according to thep-order of the edge finite elemens used,as:

Note that equations(80)and(81)can be expressed in terms ofωhp(κ),i.e.

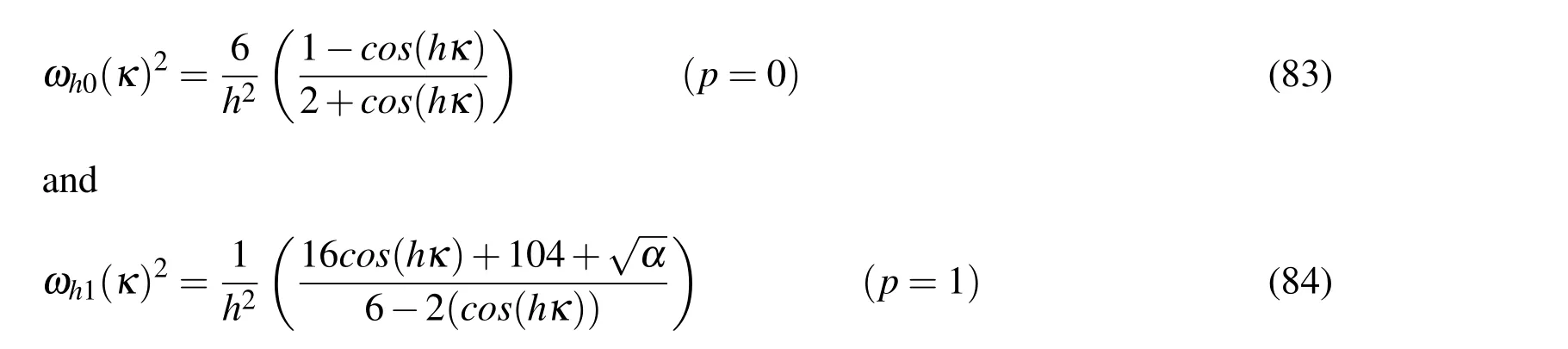
respectively,whereα=(16cos(hκ)+104)2−4(cos(hκ)−3)(cos(hκ)−1).Figure 6(a)depicts the comparison between the exact phase velocityc=ω/|κ |of the continuous problem(considerc=1,see equation(53))and the numerical phase velocity when expressions(83)and(84),are substituted,in equation(82).Figure 6(b)depicts a closer view of Figure 6(a)that estimates,for example,the largest possible value of the parameterhso that the estimated phase error is less than 0.01%.To do so,simply observe the points where the velocity curves reach the value 1.0001,i.e.,κh≈0,05 andκh≈0,62 for Whitney and Nédélec elements,respectively.

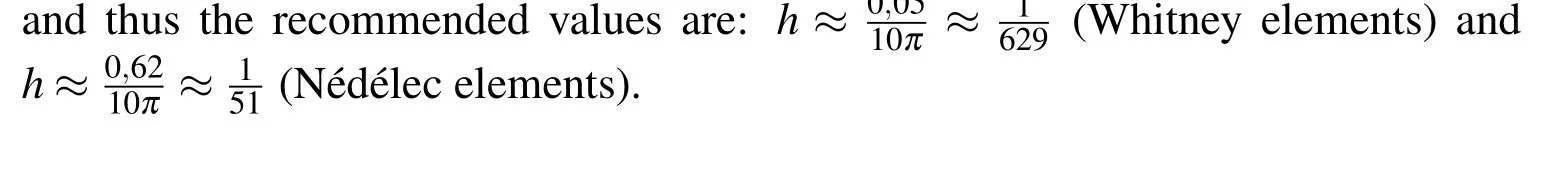
Equations(83)and(84)are employed to show the phase velocity approximation for a fixedκand an increasingn.This is shown in Figures 7(a)and 7(b)for three differentκvalues.As expected,it is clear that improving the approximation forc=1 requires smallerhvalues for larger frequency numbers,in a similar way followed by the approximate with edge finite element,see Figures 5(a)and 5(b).Therefore,we can characterize the error in the phase velocity can be characterized as error estimator in the edge finite element approximation.

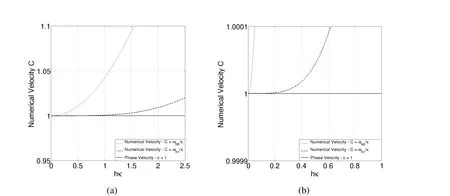
Figure 6:(a)Numerical phase velocity for Whitney and Nédélec elements,and phase velocity c=1.;(b)Closer view Figure 6(a)

7 Conclusion

In this work the edge finite elements space of zero-order and first-order,known by Whitney elements and Nédélec elements,respectively,were described,furthermore,the hierachical basis function set to each finite element studied were built.A brief presentation of the second order time harmonic Maxwell system was also presented,together with some numerical experiments concerned with its solutions.Note that some interesting results in the approximation were found:The results revealed phase differences between the approximate and the exact solutions when a fixed wave vector and a fixed temporal frequency.Another aspect that deserves attention is the presence of an amplitude difference when the frequency is changed.Two lemmas,which show a clear relationship between the scalar homogeneous Helmholtz equation and the second order time harmonic Maxwell system were presented,turning possible to adapt the dispersive effects,caused by finite element approximation of the Helmholtz equation,for the second order time harmonic Maxwell system approximation.The goal arises in the search of the proper mesh parameter,which provides quantitative information about the level of mesh re finement and necessary approximation in order to control the dispersive effects.For simplicity,this analysis was restricted to plane waves propagating with an angle of 45 degrees with the horizontal(as in the numerical experiments presented).Note that plane waves propagating in other directions presents no additional dif ficulties.Due to the numerical experiments it was observed that the error in the approximation by edge finite element have a strong correlation with the phase velocity error from the analyzed problem.This evidence suggests that the numerical phase velocity de fined from the discrete relation dispersion can be used as an error estimator in the approximation of the second order time harmonic Maxwell system by edge finite element method.

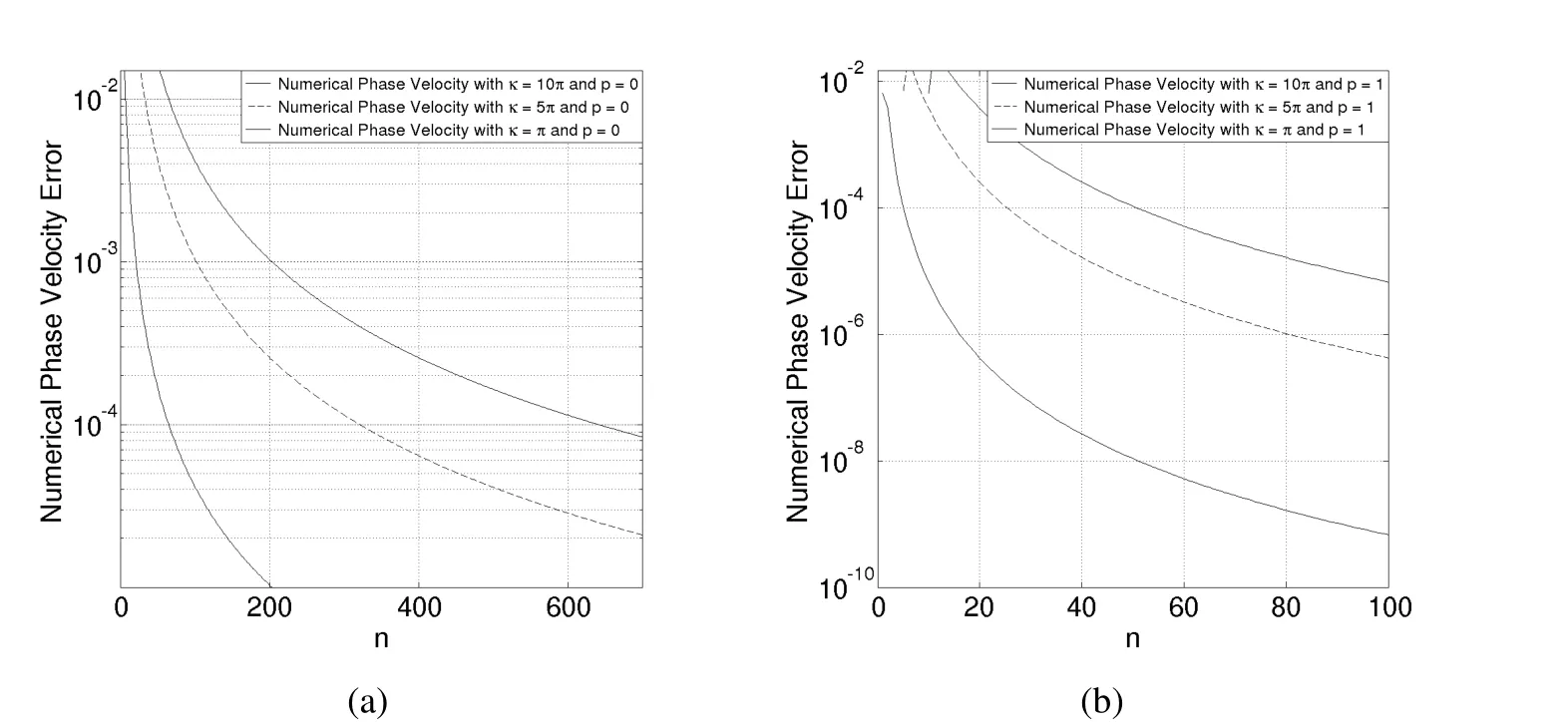
Figure 7:(a)Error between the phase velocity of the continuous problem and the numerical phase velocity for Whitney elements;(b)Nédélec elements of first order.The number of elements in the mesh is given by n2,where the mesh parameter is h=1/n.(see Figure 2).

Adjerid,S.(2002):Hierarchical finite element bases for triangular and tetrahedral elements.Comput.Methods Appl.Mech.Engrg.,vol.190,pp.2925–2941.

Ainsworth,M.(2003):Discrete dispersion for hp-version finite element approximation at high wavenumber.SIAM J.Numer.Analysis,vol.42,pp.553–575.

Ainsworth,M.;Coyle,J.(2001): Hierarchic hp-edge element families for Maxwell’sequationson hybrid quadrilateraland triangularmeshes.Comput.Methods Appl.Mech.Engrg.,vol.190,pp.6709–6733.

Babuška,I.;Ihlenburg,F.(1995): Dispersion analysis and error estimation of Galerkin finite element methods for the Helmholtz equation.International Journal for Numerical Methods in Engineering,vol.38,pp.3745–3774.

Boff i,D.;Perugia,I.(1999):Computation model of electromagnetic resonator:analysis of edge element approximation.SIAM J.Numer.Ana.,vol.36,pp.1264–1290.

Christon,M.(1999):The influence of the mass Matrix on the dispersive nature of the semi-discrete,second-order wave equation.Methods Appl.Mech.Engrg.,vol.173,pp.146–166.

Ciarlet,G.(1978):The Element Method for Elliptic Problems.North-Holland Pub,New York.

Colton,D.;Kress,R.(1983):Integral Equations Methods in Scattering Theory.John Wiley and Sons InC.,New York.

Greenleaf,A.et al.(2007): Full-Wave Invisibility of Active Devices at All Frequencies.Communications in Mathematical Physics,vol.275,pp.749–789.

Harari,I.et al.(1996): Recent Developments in Finite Element Methods for Structural Acoustic.Archives of Computational Methods in Engineering,vol.36,pp.131–311.

Ihlenburg,F.;Babuška,I.(1997): Finite element solution of the Helmholtz equation with high wave number.Society for Industrial and Applied Mathematics,vol.34,pp.315–358.

Jackson,J.D.(1999):Classical Electrodynamics.John Wiley and Sons InC.,Berkeley.

Jin,J.(2002):The Finite Element Method in Electromagnetism Second Edition.John Wiley and Sons InC.,New York.

Kaplan,W.(1970):Advanced Calculus.House of Electronics Industry,New York.

Kreyszig,E.(1978):Introductory Functional Analysis With Applications.John Wiley and Sons,New York.

Macedo,A.(1988):Eletromagnetismo.Guanabara,Rio de Janeiro.

Monk,P.(1991):A finite element method for approximating the time-harmonic Maxwell equation.Numerische Mathematik,vol.63,pp.243–261.

Monk,P.(2003): A simple Proof of Convergence for an Edge Element Discretization of Maxwell Equations.Lecture Notes in Computational Science and Engineering,vol.28,pp.127–141.

Monk,P.(2003):Finite Element Methods for Maxwell’s Equations.Oxford Science Publications,New York.

Monk,P.;Cohen,G.(1998): Gauss point mass lumping schemes for Maxwell equations.Numerical Methods for PDEs,vol.14,pp.63–88.

Monk,P.;Parrot,A.(1994): Dispersion analysis of finite element methods for Maxwell equations.SIAM J.Sci.Comput.,vol.15,pp.916–937.

Nédélec,J.(1980):Mixed finite elements in R3.Numerische Mathematik,vol.35,pp.315–341.

Nédélec,J.(1986): A new family of mixed finite elements in R3.Numerische Mathematik,vol.50,pp.57–81.

Olver,F.et al.(2010):NIST-Handbook of mathematical functions.Cambridge University Press,New York.

Reddy,B.(1986):Funcional Analysis and Boundary-Value Problems:an Introductory Treatment.John Wiley and Sons,New York.

Soares,D.et al.(2008): Numerical Computation of Electromagnetic Fields by the Time-Domain Boundary Element Method and the Complex Variable Method.Computer Modeling in Engineering&Sciences,vol.25,no.1,pp.1–8.

Thompson,L.;Pinsky,P.(1994):Complex wavenumber Fourier analysis of the p-version finite element method.Computat.Mech.,vol.13,pp.255–275.

Whitney,H.(1957):Geometry Integration Theory.Princeton University Press.,New Jersey.

Zhang,X.etal.(2014):Wave Propagation in Piezoelectric Rodswith Rectangular Cross Sections.Computer Modeling in Engineering&Sciences,vol.100,no.1,pp.1–17.