Non Probabilistic Solution of Fuzzy Fractional Fornberg-Whitham Equation

S.Chakraverty and Smita Tapaswini

1 Introduction

Fractional order differential equations have become an important research area due to its wide range of application in science and engineering.Many important works have been reported regarding fractional calculus in the last few decades.Several excellent books related to this have also been written by different authors representing the scope and various aspects of fractional calculus such as in[Podlubny(1999);Miller and Ross(1993);Oldham and Spanier(1974);Samko et al.(1993);Kiryakova(1993)].These books also give an extensive review on fractional derivative and its applications which may help the reader for understating the basic concepts of fractional calculus and its application.Most fractional differential equationsdo nothave exactanalytic solutions.Asregards,many authorshave developed various numerical methods to solve fractional differential equations[Li(2014);Chen et al.(2014);Pang et al.(2014)].

Study of travelling wave problem plays a very important role in many areas of physics.The Fornberg-Whitham equation is a type of traveling wave solutions called kink-like or antikink like wave solutions.This equation is analyzed by various authors[Abidi and Omrani(2010);Lu(2011);Fornberg and Whitham(1978);Nuseir(2012);He et al.(2010);Zhou and Tian(2009);Zhou and Tian(2008);Mahmoudi and Kazemian(2012);Sakar and Erdogan(2013);Sakar and Erdogan(2012);Merdan etal.(2012)].Abidiand Omrani(2010)applied homotopy analysis method for solving the Fornberg–Whitham equation and compared with Adomian’s decomposition method.Variational iteration method is used by Lu(2011)to obtain the approximate solution of Fornberg–Whitham equation.Fornberg and Whitham(1978)studied numerical and theoretical study of Fornberg–Whitham equation.A new exact solution of modified Fornberg-Whitham equation is obtained by Nuseir(2012).Bifurcation theory and the method of phase portraits analysis are done by He et al.(2010)for the study of modified Fornberg–Whitham equation.Zhou and Tian(2009)investigated a new travelling wave solution viz.periodic and solitary wave solution.Also Zhou and Tian(2008)used bifurcation method to study the solution of Fornberg–Whitham equation.The homotopy analysis method is successfully implemented by Mahmoudi and Kazemian(2012)to obtain an approximate analytical solution.Sakar and Erdogan(2013)compared the solution obtained by the homotopy analysis method and Adomian’s decomposition method for the solution of time fractional Fornberg–Whitham equation.Sakar and Erdogan(2012)used variational iteration method for the solution of time-fractional Fornberg–Whitham equation.Differential transformation method is used by Merdan et al.(2012)to obtain numerical solution.Behera and Chakraverty(2013)successfully applied homotopy perturbation method to obtain the numerical solution of fractionally damped beam equation.Fractional B-Spline method was implemented by Jafari et al(2013)to get the numerical solution of fractional differential equations.Also Jafari et al.(2013)applied homotopy analysis method for solving fractional Abel differential equation.We may observe from the above cited papers that the parameters and initial conditions are considered as crisp in their investigations.But in actual practice,rather than the particular value,only uncertain or vague estimates about the variables and parameters are known.Because those are found in general by some observation,experiment or experience.So,to handle these uncertainties and vagueness,one may use fuzzy parameters and variables in the governing differential equations.

As such,both uncertainty and fractional differential equations play a vital role in real life problems.Some recent contributions to the theory of fuzzy differential equation and fuzzy fractional differential equations can be found in[Khastan et al.(2011);Bede et al.(2007);Jafari et al.(2012);Malinowski(2013);Akin et al.(2013);Agarwal et al.(2010);Arshad and Lupulescu(2011a);Arshad and Lupulescu(2011b);Jeong(2010);Wang and Liu(2011);Allahviranloo et al.(2012);Khodadadi and Celik(2013);Mohammed(2011);Salahshour et al.(2012);Salah et al.(2013);Behera and Chakraverty(2014);Ahmad et al.(2013);Allahviranloo et al.(2013);Tapaswini and Chakraverty(2013);Ghaemi et al.(2013)].The concept of fuzzy fractional differential equation was introduced recently by Agrawal et al.(2010).Arshad and Lupulescu(2011a)proved some results on the existence and uniqueness of solutions of fuzzy fractional differential equations based on the concept of fuzzy differential equations of fractional order introduced by Agrawal et al.(2010).Arshad and Lupulescu(2011b)investigated the fractional differential equation with the fuzzy initial condition.Jeong(2010)discussed existence and uniqueness results for fuzzy fractional di?erential equations with in?nite delay.Boundary value problem for fuzzy fractional differential equations with finite delay has been solved by Wang and Liu(2011).They established the existence of a solution by contraction mapping principle.Based on Riemann–Liouville H-differentiability,Allahviranloo et al.(2012)studied explicit solutions of fuzzy/uncertain fractional differential equations.Variational iteration method is applied by Khodadadi and Celik(2013)for the solution of fuzzy fractional differential equations.Mohammed et al.(2011)applied differential transform method for solving fuzzy fractional initial value problems.Salahshour et al.(2012)developed Riemann-Liouville differentiability by using Hukuhara difference called Riemann-Liouville H-differentiability and solved fuzzy fractional differential equations by Laplace transforms.Recently Salah et al.(2013)applied homotopy analysis transform method for the solution of fuzzy fractional heat equation.In Salah et al.(2013),the authors have solved fuzzy fractional differential equation by solving lower and upper bound problems separately to get the solution bounds.Behera and Chakraverty(2014)successfully applied HPM method to find uncertain impulse response of imprecisely defined fractional order mechanical system.Zadeh’s Extension Principle is used by Ahmad et al.(2013)for the solution of fuzzy fractional differential equations.Allahviranloo et al.(2013)solved the fuzzy fractional differential equations under generalized fuzzy Caputo derivative.Numerical solution of fuzzy arbitrary order predator-prey system is obtained by Tapaswini and Chakraverty(2013).Ghaemi et al.(2013)solved a fuzzy fractional kinetic equation of acid hydrolysis reaction.

HPM is found to be a powerful tool for the analysis of linear and non-linear physical problems.HPM was first developed by He(1999;2000)and then many authors applied this method to solve various linear and non-linear functional equations of scienti fic and engineering problems.The solution is considered as the sum of infinite series,which converges rapidly.In the homotopy technique(in topology),a homotopy is constructed with an embedding parameterp∈[0,1]which is considered as a “small parameter”.Very recently homotopy perturbation method has been applied to a wide class of physical problems[Chen and Jiang(2010);Yazdi(2012);Abolarin(2013);Tapaswini and Chakraverty(2013a);Tapaswini and Chakraverty(2013b)].

In the present analysis,HPM is used for the numerical solution of uncertain nonlinear fractional Fornberg-Whitham Equation subject to fuzzy initial condition.Uncertainty in the initial condition is defined in term of triangular and Gaussian fuzzy numbers.Literature review reveals that fuzzy fractional differential equations are always converted to two crisp fractional differential equations in general to obtain the solution bounds.But in this paper,a new approach is proposed based on a double parametric form of fuzzy numbers as defined in Definition 2.4 where fractional fuzzy differentialequation hasbeen converted to a single crisp parametric fractional differential equation.Finally the corresponding single crisp parametric fractional differential equation may be solved by any known numerical method symbolically to obtain the solution in the double parametric form.Then substituting the parametric values one may obtain the final solution bounds.

This paper is organized as follows.In Section 2,some basic preliminaries related to the present investigation are given.HPM is applied with the proposed technique in Section 3 to solve fuzzy fractional Fornberg-Whitham equation.In Section 4,uncertain solutions for different type of fuzzy initial condition are given.Next numerical results and discussions are presented.Finally in the last section conclusions are drawn.

2 Preliminaries

In this section,we present some notations,definitions and preliminaries which are used further in this paper[Zimmermann(2001);Jaulin et al.(2001);Hanss(2005);Ross(2004)].

Definition 2.1Fuzzy number

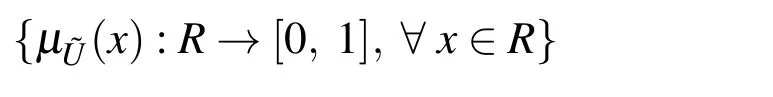
where,µ˜Uis called the membership function of the fuzzy set and it is piecewise continuous.

Definition 2.2Triangular fuzzy number

A triangular fuzzy number˜Uis a convex normalized fuzzy set˜Uof the real lineRsuch that

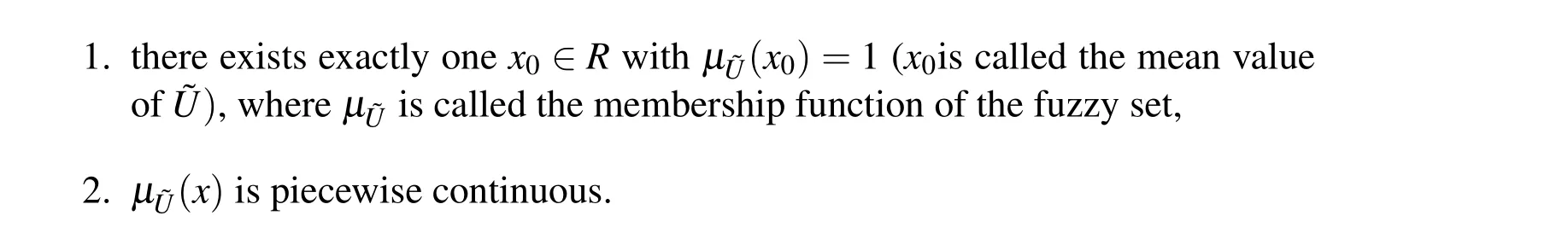
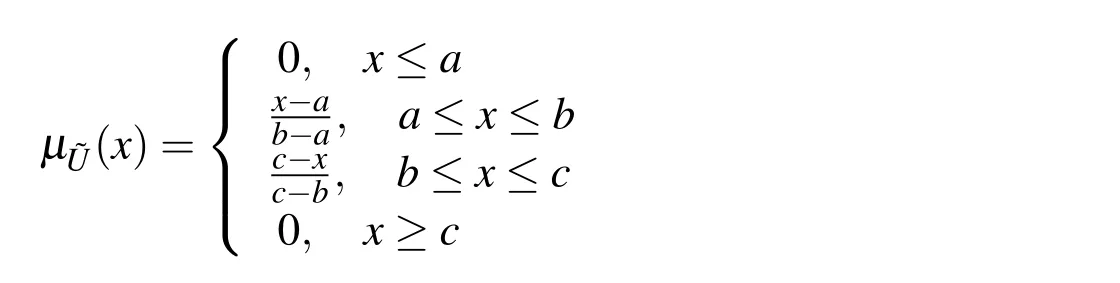
Definition 2.3Gaussian fuzzy number

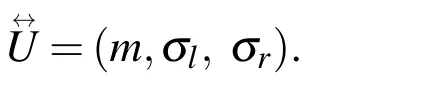
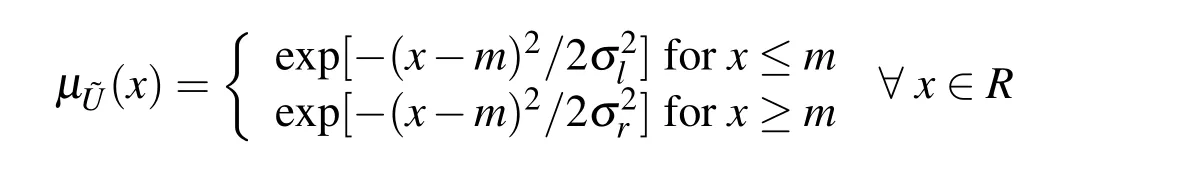
where,the modal value is denoted asmandσl,σrdenote the left-hand and righthand spreads(fuzziness)corresponding to the Gaussian distribution.

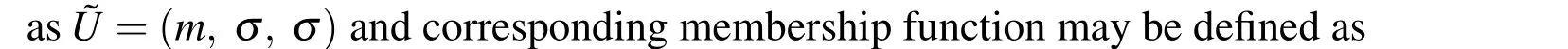
where,γ=1/2σ2.

Definition 2.4Single parametric form of fuzzy numbers

Similarly,for symmetric Gaussian fuzzy numberU=(m,σ,σ)in parametric form is written as

Ther−cut form is known as parametric form or single parametric form of fuzzy numbers.

It may be noted that the lower and upper bounds of the fuzzy numbers satisfy the following requirements

Definition 2.5Double parametric form of fuzzy number

Definition 2.6Fuzzy arithmetic

3 Double parametric based fuzzy fractional Fornberg-Whitham equation

First we convert the fuzzy fractional Fornberg-Whitham equation in-to an interval based fuzzy fractional Fornberg-Whitham equation using single parametric form of fuzzy numbers.Then the interval based differential equation is reduced to crisp differential equation by using double parametric form of fuzzy numbers.Next,we have applied HPM to obtain the solution in double parametric form.

Let us now consider the fuzzy fractional Fornberg-Whitham equation

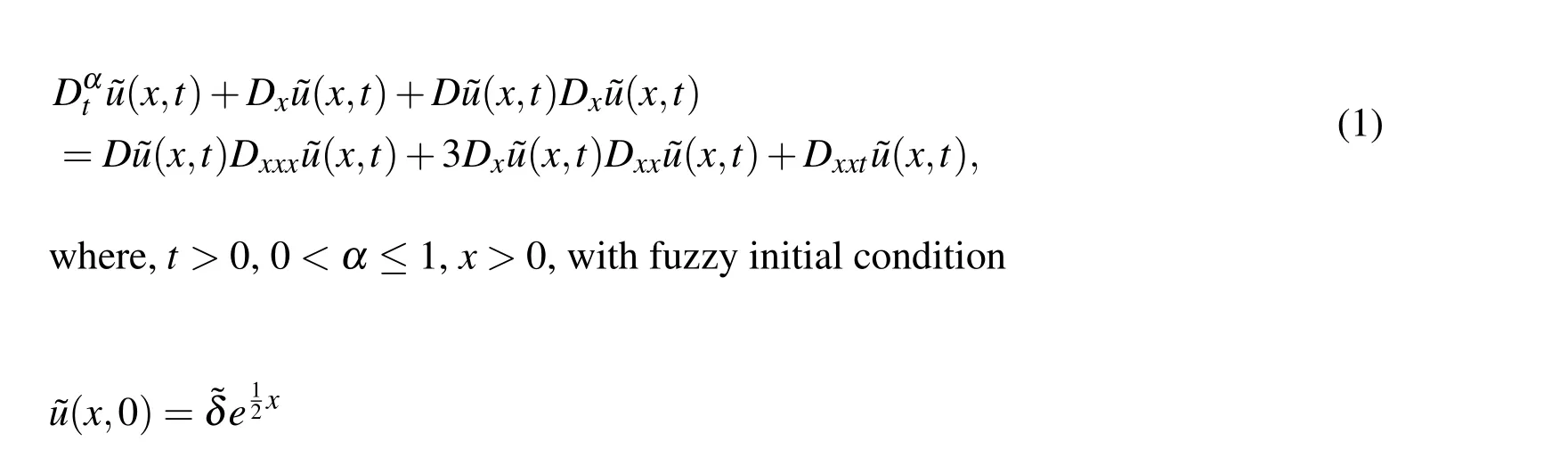
Here the initial condition has been taken as fuzzy with an idea that the condition may actually be uncertain viz.due to the error in observation or experiment etc.where we may take the error or uncertainty in term of fuzzy triangular or Gaussian membership functions.As such,this will make the governing differential equation as uncertain and the corresponding outcome or the output(result)will be in uncertain form.This way we may have the actual essence of the uncertainty.So,we need to have efficient methods to handle these problems.

According to the single parametric form we may write the above fuzzy fractional Fornberg-Whitham equation(Eq.(1))as

subject to fuzzy initial condition

Using the double parametric form(as discussed in Definition 2.4),Eq.(2)can be expressed as

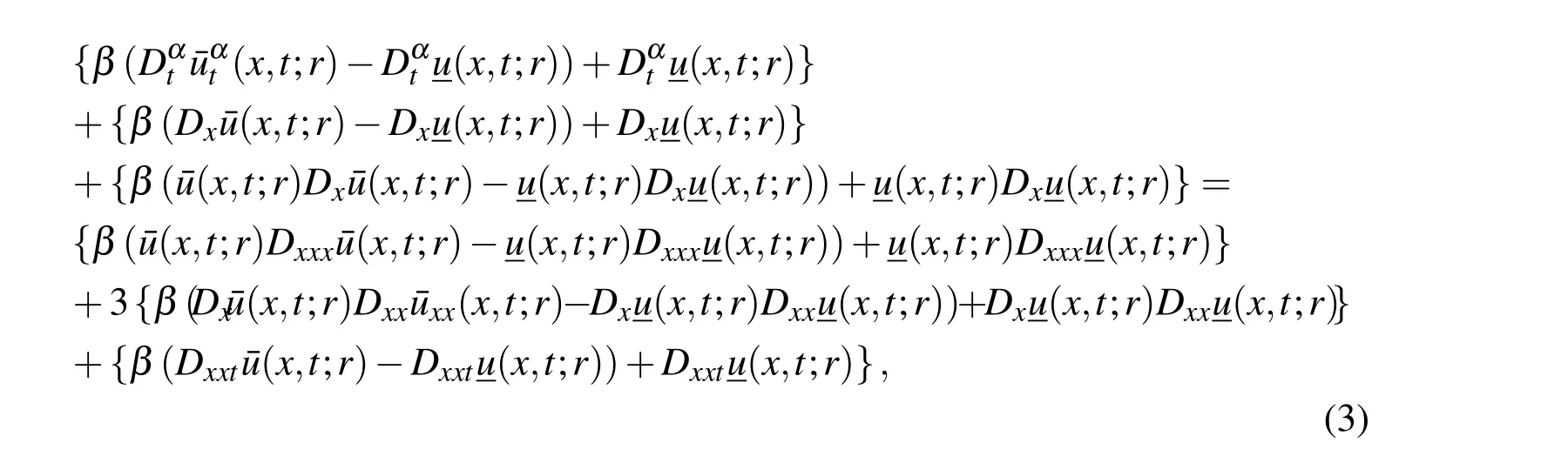
subject to the fuzzy initial condition

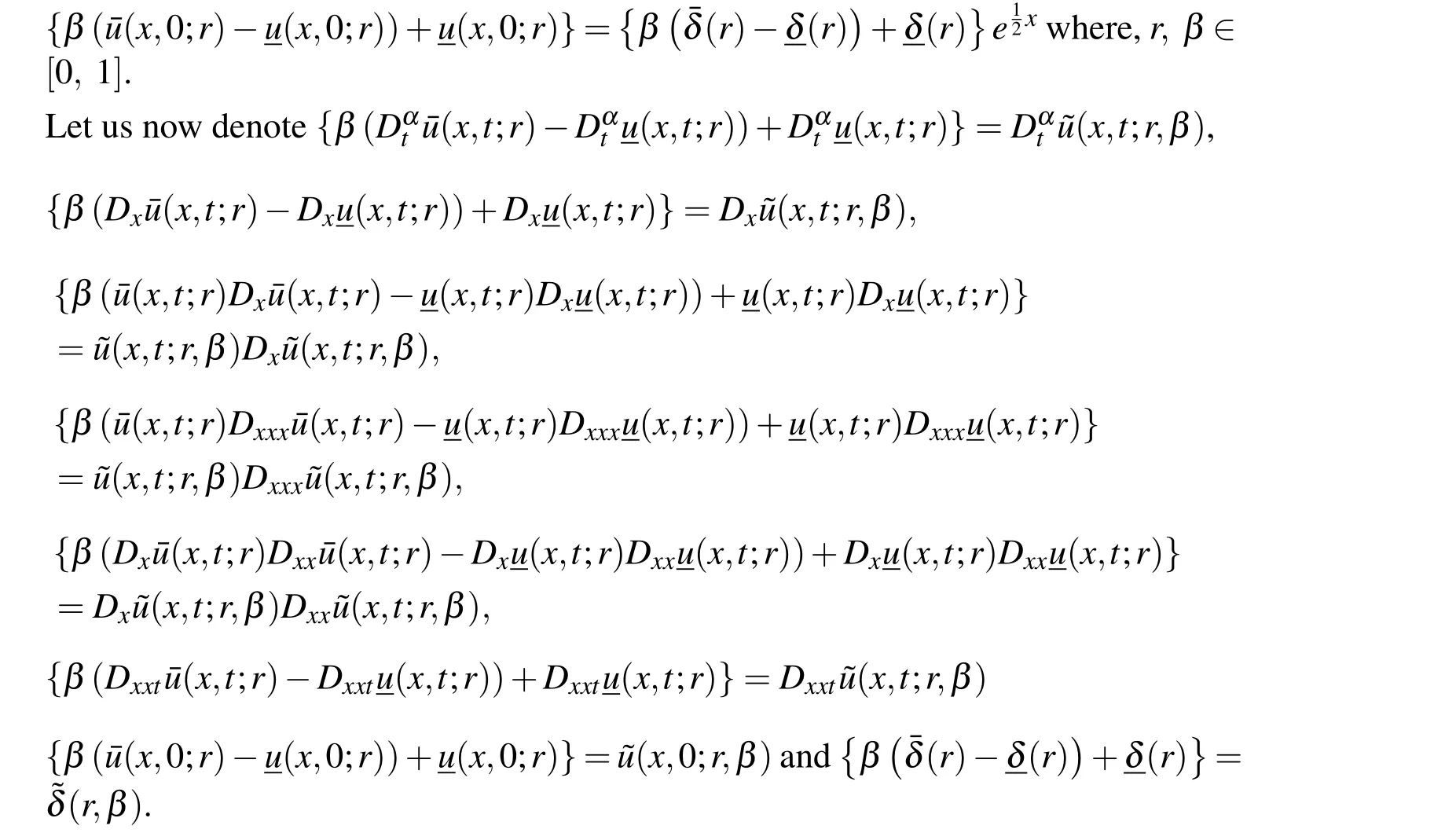
Substituting these in Eq.(3)we get

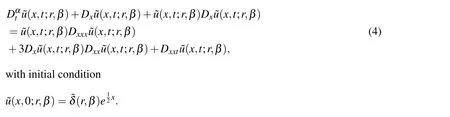
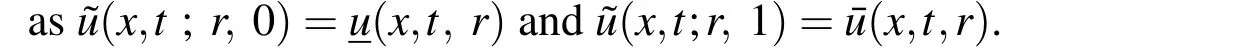
Solution by HPM[He(1999;2000)]using proposed methodology

We have applied HPM to solve Eq.(4).According to HPM,we may construct a simple homotopy for an embedding parameterp∈[0,1],as follows

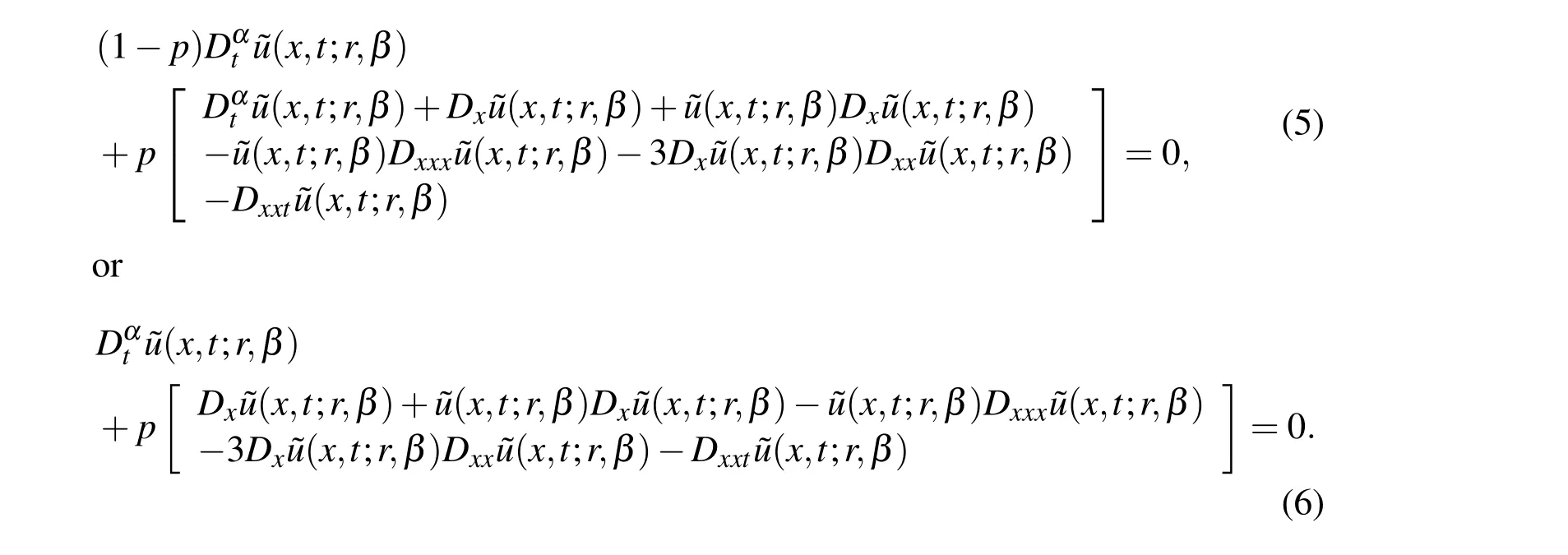
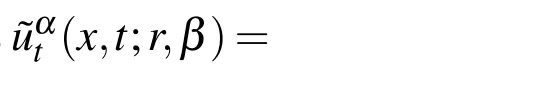
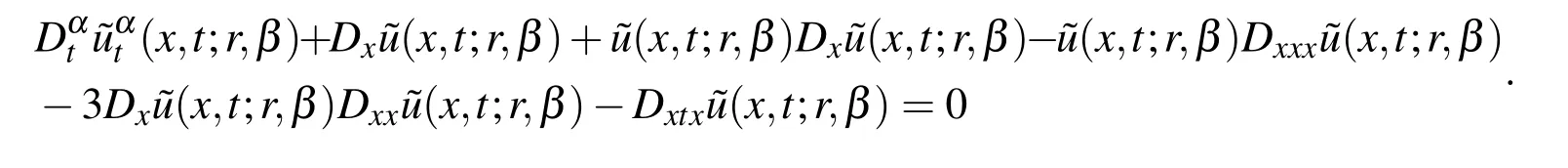
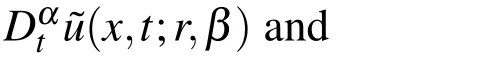
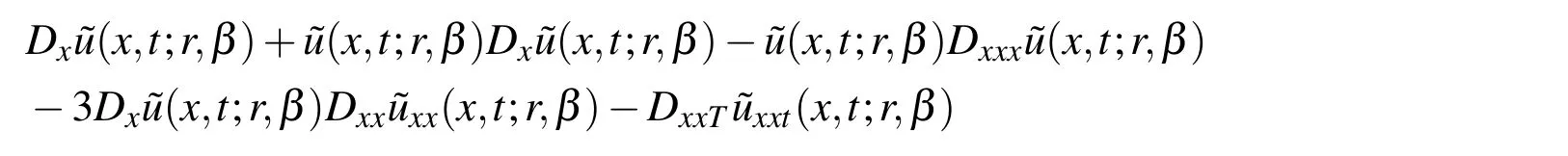
are called homotopic.Next,we can assume the solution of Eq.(5)or(6)as a power series expansion inpas

and so on.

该模式规范了患者管理，经管理的65例患者，HbA1c水平较管理前下降明显，上转患者通过“绿色通道”得到方便；通过仁济医院专家的指导，全科医生诊疗水平和能力得到提高，特别是在胰岛素使用方面更加规范、降糖药物联合使用方面更加合理、降糖药物禁忌症方面更加重视、对患者的用药指导方面更加全面。

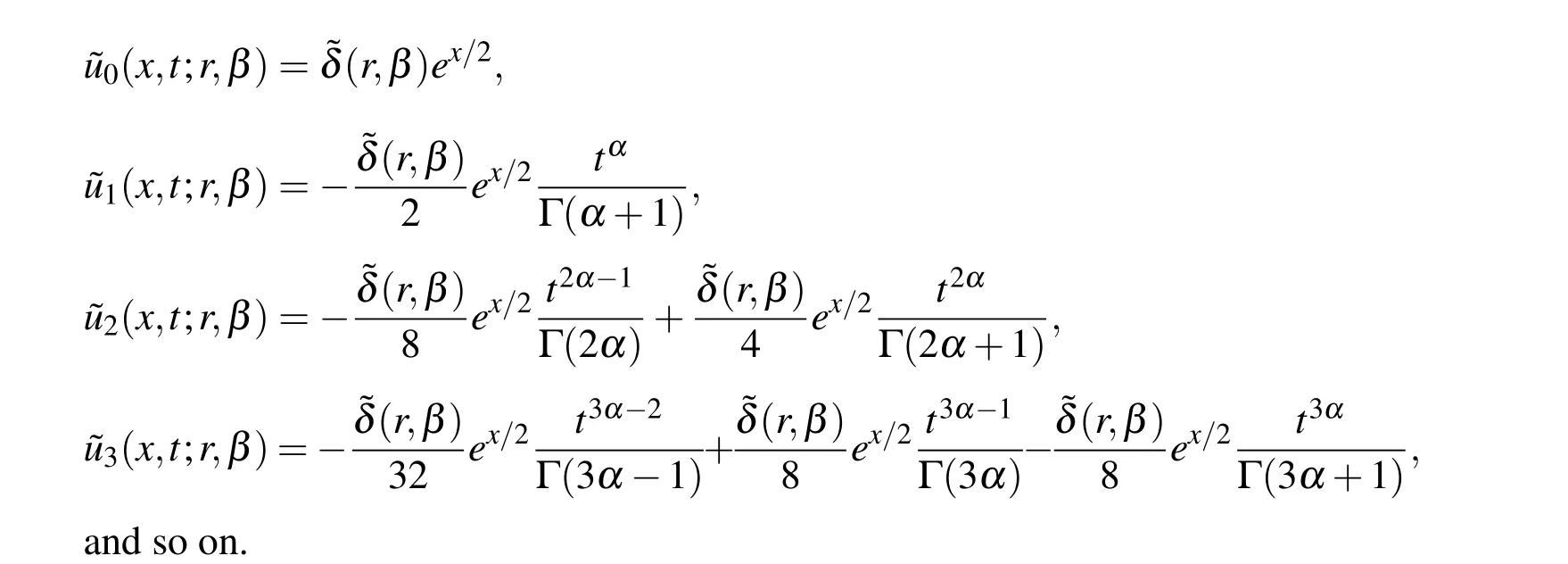
Now substituting these terms in Eq.(7)withp→1we get the approximate solution of Eq.(4)as

The above series obtained by HPM converges very rapidly and only few terms are required to get the approximate solutions.The proof may be found in[He(1999;2000)].

4 Solution bounds for different fuzzy initial conditions

In this section we have considered different fuzzy initial conditions as discussed in the following cases to find the uncertain solution bounds for fuzzy fractional Fornberg-Whitham equation.

Case 1:Triangular fuzzy initial condition viz.

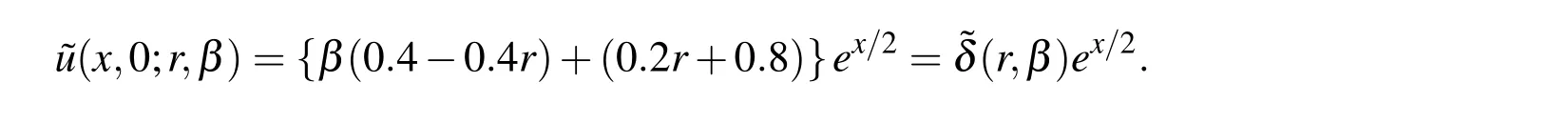
The solution can be written as

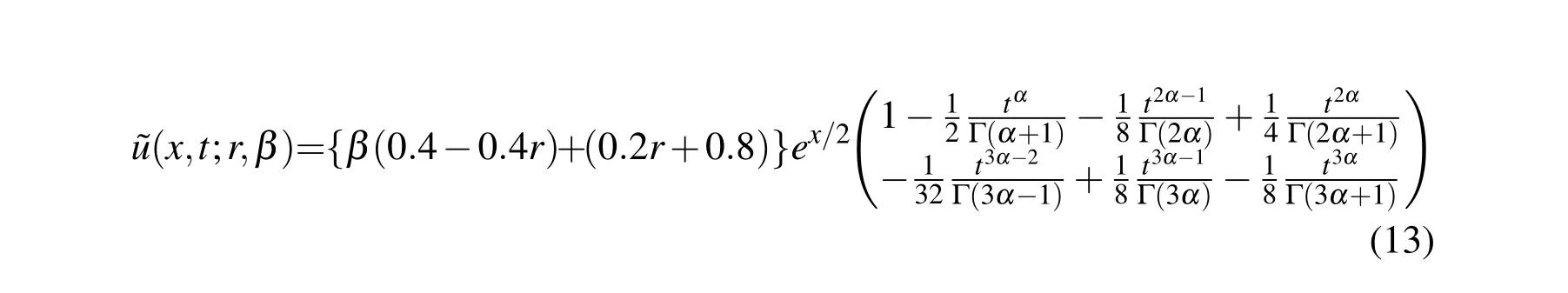
To obtain the solution bounds in single parametric form,we may substituteβ=0 and 1 for lower and upper bounds of the solution respectively.So we get

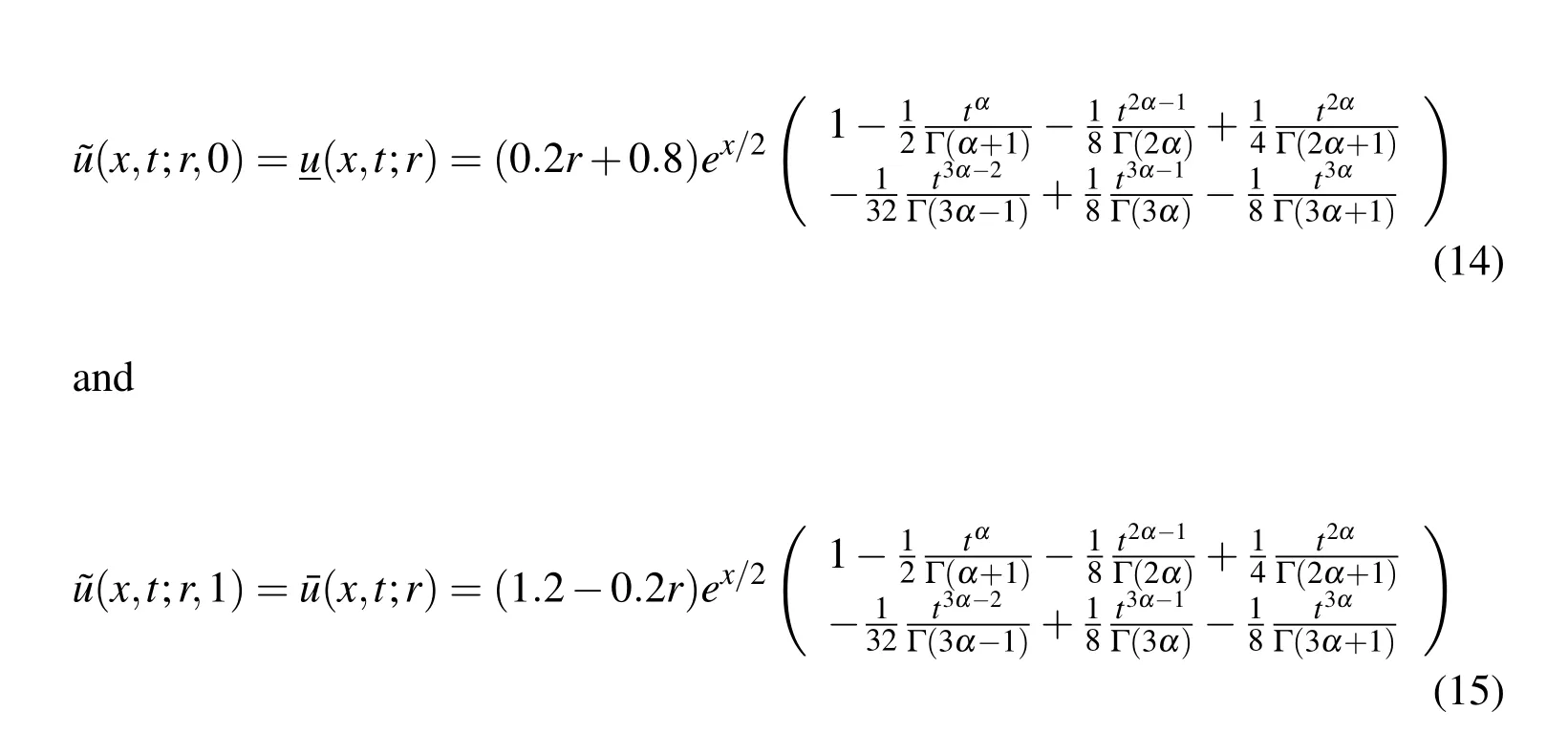
One may note that in the special case whenr=1 the results(crisp)obtained by the proposed method are exactly same as that of the solution obtained by Sakar&Erdogan[17]

Case 2:Gaussian fuzzy initial condition viz.

Again,by applying the proposed procedure,we get the solution as

Puttingβ=0 and 1 in˜u(x,t;r,β)we get the lower and upper bounds of the fuzzy solutions respectively as

The solution obtained by the proposed method forr=1 is again found to be exactly same as that of(crisp result)Sakar and Erdogan(2013)

5 Numerical results and discussions

Numerical results for fuzzy fractional Fornberg-Whitham equation with different fuzzy initial conditions are computed.Obtained results of the present analysis are compared with the existing solution of Sakar&Erdogan(2013)in special cases to show the validation of the proposed analysis.Computed results are depicted in term of plots.

Triangular and Gaussian fuzzy solutions for Cases 1 and 2 are depicted in Figs.1 and 2 respectively by varying the timetfrom 0 to 3 andx=1 withα=0.3.Next,interval solutions for.x=1 in both the cases have been given in Figs.3 to 4 forx=1 andα=0.3,0.7,0.9,1.It may be worth mentioning that in both the cases,present results exactly agree with the solution of Sakar&Erdogan(2013)in special case ofr=1 Also it is interesting to note from Figs.3 and 4 that the left and right bounds of the uncertain fluid velocity that is˜u(x,t)(with particular values ofα,randx)gradually decreases with the increase of the fractional orderαand timet.Figs.5 and 6 show for particular values ofr=0.2 andt=1,the uncertain fluid velocity increases with increase inxand decreases with the increase of fractional orderα.

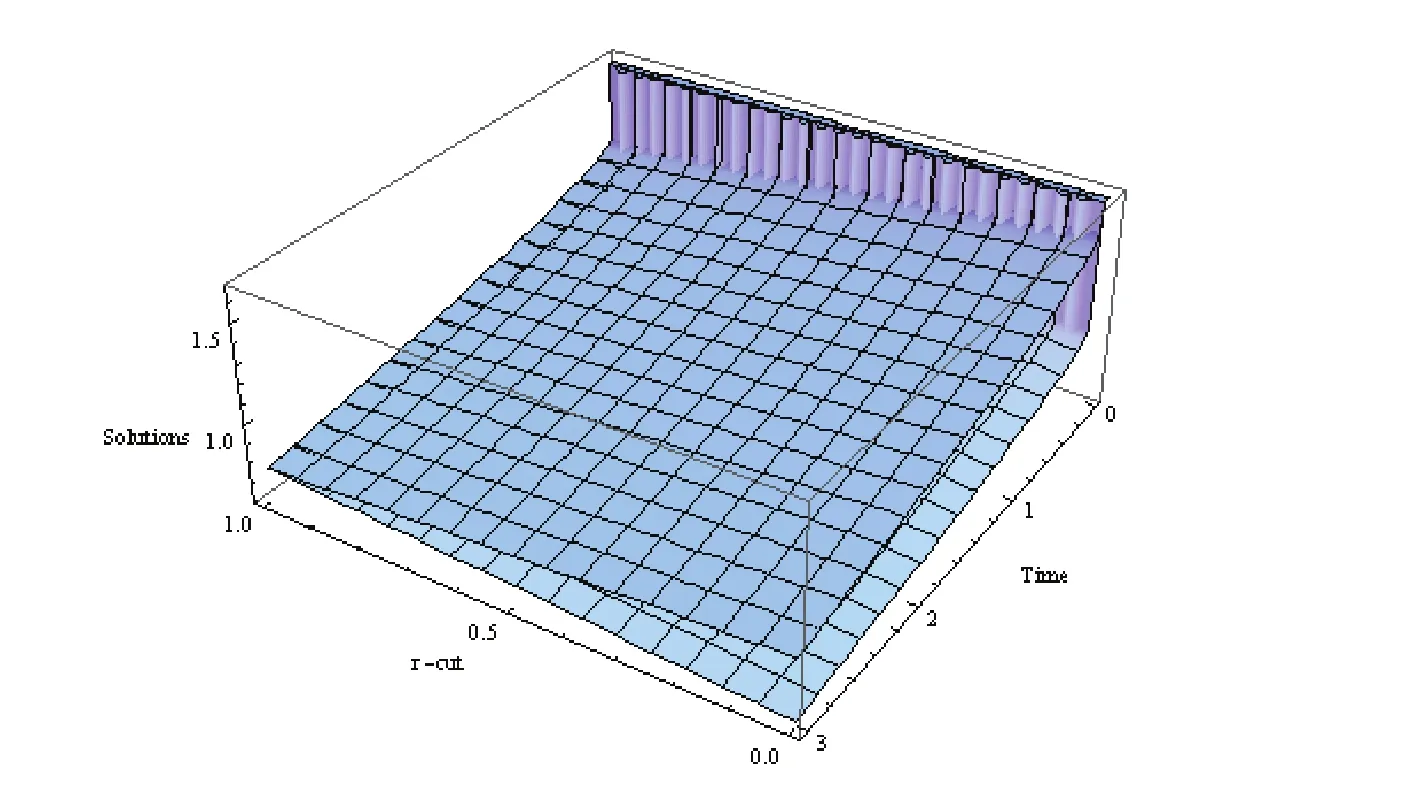
Figure 1:Fuzzy solution for Case 1.

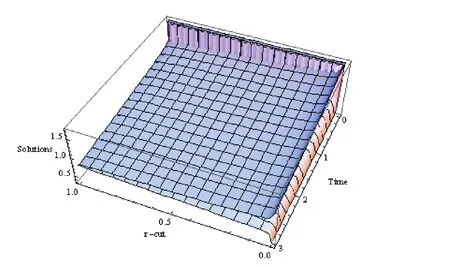
Figure 2:Fuzzy solution for Case 2.

Figure 3:Interval solutions for Case 1 at x=1.

Figure 4:Interval solutions for Case 2 at x=1.

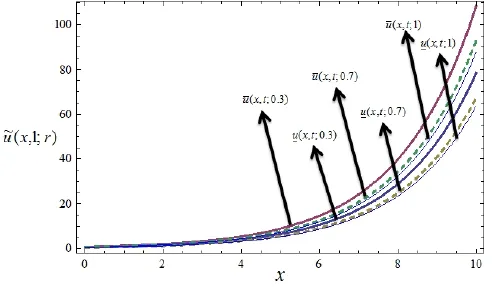
Figure 5:Interval solutions for Case 1 at t=1.

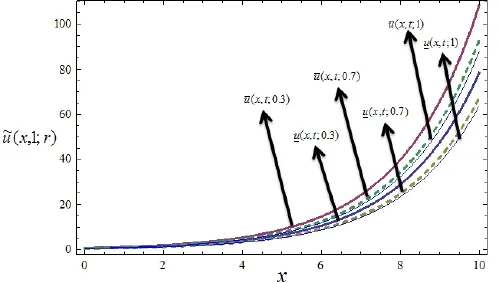
Figure 6:Interval solutions for Case 2 at t=1.

6 Conclusions

In this paper double parametric form of fuzzy numbers has been successfully employed for the solution of fuzzy fractional Fornberg-Whitham equation with triangularand Gaussian fuzzy initialcondition using the homotopy perturbation method.The double parametric form approach is found to be easy and straight-forward.It is interesting to note in both the examples that the lower solution is equal to the upper solution whenr=1.Though the solution by HPM is of the form of an infinite series but it can be written in a closed form.The main advantage of HPM may also be seen in the process of solution of uncertain differential equations that it has the capability to achieve exact solution and rapid convergence with few terms.

Acknowledgement:The authors would like to thank the Editor and anonymous reviewers for their valuable suggestions and comments to improve the paper.Also,we would like to thank Mr.Diptiranjan Behera,National Institute of Technology Rourkela for his valuable help.The second author would like to thank the UGC,Government of India,for financial support under Rajiv Gandhi National Fellowship(RGNF).

Abidi,F.;Omrani,K.(2010):The homotopy analysis method for solving the Fornberg–Whitham equation and comparison with Adomian’s decomposition method.Comput.Math.Appl.vol.59,pp.2743–2750.

Abolarin,O.E.(2013):New improved variational homotopy perturbation method for Bratu-type problems.American J.Comput.Math.,vol.3,pp.110-113.

Agarwal,R.P.;Lakshmikantham,V.;Nieto,J.J.(2010):On the concept of solution for fractional differential equations with uncertainty.Nonlinear Analy.:Theory,Methods Appl.,vol.72,pp.2859–2862.

Ahmad,M.Z.;Hasan,M.K.;Abbasbandy,S.(2013)Solving fuzzy fractional differential equations using Zadeh’s extension principle.Sci.World J.,vol.2013,pp.1-11.

Akin,O.;Khaniyev,T.;Oruc,O.;Turksen,I.B.(2013):An algorithm for the solution of second order fuzzy initial value problems.Expert Syst.Appl.,vol.40,pp.953-957.

Arshad,S.;Lupulescu,V.(2011):On the fractional differential equations with uncertainty.Nonlinear Anal.:Theory,Methods Appl.,vol.74,pp.3685-3693.

Arshad,S.;Lupulescu,V.(2011):Fractional differential equation with the fuzzy initial condition.Elect.J.Diff.Equ.,vol.2011,pp.1–8.

Allahviranloo,T.;Gouyandeh,Z.;Armand,A.(2013):Fuzzy fractional differential equations under generalized fuzzy Caputo derivative.J.Intelligent Fuzzy Syst.,vol.26,pp.1481-1490.

Allahviranloo,T.;Salahshour,S.;Abbasbandy,S.(2012)Explicit solutions of fractional differential equations with uncertainty.Soft Comp.,vol.16,pp.297-302.

Bede,B.;Rudas,I.;Bencsik,A.(2007):First order linear fuzzy differential equations under generalized differentiability.Inf.Sci.,vol.177,pp.1648-1662.

Behera,D.;Chakraverty,S.(2013):Numerical solution of fractionally damped beam by homotopy perturbation method.Cent.Eur.J.Phys.,vol.11,pp.792-798.

Behera,D.;Chakraverty,S.(2014):Uncertain impulse response of imprecisely defined half order mechanical system.Annals Fuzzy Math.Inf.,vol.7,pp.401-419.

Chen,Y.;Han,X.;Liu,L.(2014):Numerical solution for a class of linear system of fractional differential equations by the Haar wavelet method and the convergence analysis.Comput.Model.Eng.Sci.,vol.97,pp.391-405.

Chen,A.;Jiang,G.(2010):Periodic solution of the Duffing-Van der Pol oscillator by homotopy perturbation method.Int.J.Comput.Math.,vol.87,pp.2688-2696.

Fornberg,B.;Whitham,G.B.(1978):A numerical and theoretical study of certain nonlinear wave phenomena.Phil.Trans.Royal Soc.London A.,vol.289,pp.373–404.

Ghaemi,F.;Yunus,R.;Ahmadian,A.,Salahshour,S.;Suleiman,M.;Saleh,S.F.(2013):Application of fuzzy fractional kinetic equations to modelling of the acid hydrolysis reaction.Abst.Appl.Analy.,vol.2013,pp.1-19.

Hanss M.(2005):Applied Fuzzy Arithmetic:An Introduction with Engineering Applications.Springer-Verlag,Berlin.

He,J.H.(1999):Homotopy perturbation technique.Computer Methods in Appl.Mech.Eng.vol.178,pp.257-262.

He,J.H.(2000):A coupling method of homotopy technique and perturbation technique for nonlinear problems.Int.J.Non-Linear Mech.,vol.35,pp.37-43.

He,B.;Meng,Q.;Li,S.(2010):Explicit peakon and solitary wave solutions for the modified Fornberg-Whitham equation.Appl.Math.Comput.,vol.217,pp.1976-1982.

Jafari,H.;Khalique,C.M.;Ramezani,M.;Tajadodi,H.(2013)Numerical solution of fractional differential equations by using fractional B-spline.Cent.Eur.J.Phys.doi:10.2478/s11534-013-0222-4.

Jafari,H.;Saeidy,M.;Baleanu,D.(2012):The variational iteration method for solving n-th order fuzzy differential equations.Cent.Eur.J.Phys.,vol.10,pp.76-85.

Jafari,H.;Sayevand,K.;Tajadodi,H.;Baleanu,D.(2013)Homotopy analysis method for solving Abel differential equation of fractional order.Cent.Eur.J.Phys.,doi:10.2478/s11534-013-0209-1.

Jaulin,L.;Kieffer,M.;Didrit,O.;Walter,E.(2001):Applied Interval Analysis.Springer,France.

Jeong,J.U.(2010):Existence results for fractional order fuzzy di?erential equations with infinite delay.Int.Math.Forum.,vol.5,pp.3221–3230.

Khastan,A.;Nieto,J.J.;Rodríguez-López,R.(2011):Variation of constant formula for first order fuzzy differential equations.Fuzzy Sets Syst.,vol.177,pp.20–33.

Kiryakova,V.S.(1993):GeneralizedFractionalCalculusandApplications.Longman Scientific&Technical.Longman House:Burnt Mill,Harlow England.

Khodadadi,E.;Celik,E.(2013):The variational iteration method for fuzzy fractional differential equations with uncertainty.Fixed Point Theory Appl.,vol.2013,pp.1-7.

Li,B.(2014):Numericalsolution offractionalFredholm-Volterra integro-differential equations by means of generalized hat functions method.Comput.Model.Eng.Sci.,vol.99,pp.105-122.

Lu,J.(2011):An analytical approach to the Fornberg–Whitham type equations by using the variational iteration method.Comput.Math.Appl.vol.61,pp.2010–2013.

Mahmoudi,Y.;Kazemian,M.(2012):Some notes on homotopy analysis method for solving the Fornberg-Whitham equation.J.Basic Appl.Sci.Res.vol.2,pp.2985-2990.

Malinowski,M.T.(2013):Some properties of strong solutions to stochastic fuzzy differential equations.Inf.Sci.,vol.252,pp.62-80.

Merdan,M.;Gokdogan,A.;Yıldırım A.;Mohyud-Din,S.T.(2012):Numerical simulation of fractional Fornberg-Whitham equation by differential transformation method.Abstract Appl.Anal.,vol.2012,pp.1-8.

Miller,K.S.;Ross,B.(1993):An Introduction to the Fractional Calculus and Fractional Differential Equations.John Wiley and Sons,New York.

Mohammed,O.H.;Fadhel,F.S.;Abdul-Khaleq,F.A.(2011):Differential transform method for solving fuzzy fractional initial value problems.J.Basrah Res.(Sci.).vol.37,pp.158-170.

Nuseir,A.S.(2012):New exactsolutions to the modified Fornberg-Whitham equation.Taiw.J.Math.,vol.16,pp.2083-2091.

Oldham,K.B.;Spanier,J.(1974):The Fractional Calculus,Academic Press,New York.

Pang,G.;Chen,W.;Sze,K.Y.(2014):Differential quadrature and cubature methods for steady-state space-fractional Advection-Diffusion equations.Comput.Model.Eng.Sci.,vol.97,pp.299-322.

Podlubny,I.(1999):Fractional Differential Equations.Academic Press,New York.

Ross,T.J.(2004):Fuzzy Logic with Engineering Applications.John Wiley&Sons New York.

Samko,S.G.;Kilbas,A.A.;Marichev,O.I.(1993):Fractional integrals and Derivatives-TheoryandApplications.Gordon and Breach Science Publishers Langhorne.

Sakar,M.G.;Erdogan,F.(2013):The homotopy analysis method for solving the time fractional Fornberg–Whitham equation and comparison with Adomian’s decomposition method.Appl.Math.Modell.vol.37,pp.8876-8885.

Sakar,M.G.;Erdogan,F.;Yildirim,A.(2012)Variational iteration method for the time-fractional Fornberg–Whitham equation.Comput.Math.Appl.,vol.63,pp.1382–1388.

Salahshour,S.;Allahviranloo,T.;Abbasbandy,S.(2012):Solving fuzzy fractional differential equations by fuzzy laplace transforms.Comm.Non.Sci.Num.Simul.,vol.17,pp.1372-1381.

Salah,A.;Khan,M.;Gondal,M.A.(2013):A novel solution procedure for fuzzy fractional heat equations by homotopy analysis transform method.Neu.Comp.Appl.,vol.23,pp.269–271.

Tapaswini,S.;Chakraverty,S.(2013):Numerical solution of fuzzy arbitrary order Predator-prey equations.Appl.Appl.Math.:An Int.J.,vol.8,pp.647–672.

Tapaswini,S.;Chakraverty,S.(2013):Numerical solution of uncertain beam equations using double parametric form of fuzzy numbers.Appl.Comput.Intell.Soft Comput.,vol.2013,pp.1-8.

Tapaswini,S.;Chakraverty,S.(2013):Numerical solution of fuzzy quadratic Riccati differential equation.Coupled Syst.Mech.,vol.2,pp.255-269.

Wang,H.;Liu,Y.(2011):Existence results for fractional fuzzy differential equations with finite delay.Int.Math.Forum.,vol.6,pp.2535-2538.

Yazdi,A.A.(2012):Homotopy perturbation method for nonlinear vibration anal-ysis of functionally graded plate.J.Vib.Acoust.,vol.135,pp.021012-1-6.

Zhou,J.;Tian,L.(2009):Periodic and solitary wave solutions to the Fornberg-Whitham equation.Math.Prob.Eng.,vol.2009,pp.1-10.

Zhou,J.;Tian,L.(2008)A type of bounded traveling wave solutions for the Fornberg-Whitham equation.J.Math.Anal.Appl.,vol.346,pp.255–261.

Zimmermann,H.J.(2001):Fuzzy Set Theory and its Application.Kluwer academic publishers,London.