Electronic Structure and Magnetic Properties of New Rare-earth Half-metallic Materials AcFe2O4 and ThFe2O4:Ab Initio Investigation

Jingguo YanXudong WangMan Yao and Ning Hu

1 Introduction

Half-metals,as a new kind of ideal spintronic functional materials,have drawn much attention due to their 100%spin polarization at the Fermi level and being able to control the spins of electrons and transmission of charges simultaneously to realize efficient information storage and processing[de Grootet al.(1983);Prinz(1999);Coeyet al.(2002);Kopcewiczet al.(2005);Tanet al.(2012);Zhaoet al.(2012)].Compared to ordinary semiconductor electronic devices,devices made of half-metals have such outstanding features as non-volatile,low power consumption and high integration.What’s more,more dimensions considered in the research of half-metal materials will produce more new excellent properties and more applications[Wolfet al.(2001);Minget al.(2012);Yaoet al.(2012)].To date,many half-metals have been found experimentally and theoretically[Coeyet al.(2002);Dedkowet al.(2002);Fonget al.(2004);Houet al.(2011);Chenet al.(2012)].Among them,the II B-type half-metal Fe3O4has attracted much more attention due to their special advantages,such as stable performance,larger roomtemperature spin-polarization,higher courier temperature,easy preparation[Kimet al.(2003)].However,its magnetoresistance is not large enough to give access to huge magnetoresistance effects when used as magnetic electrodes in spintronic devices.Consequently,it is an urgent mission to design new spinel half-metals with larger magnetoresistance and higher conductivity.

First principle calculation has been a very effective method to predict and analyze the properties of crystal materials and many Fe3O4based half-metals have been designed by this method[Liu,Chenet al.(2007);Liu,Wanget al.(2007);Liuet al.(2008)].However,this research effort is still in the initial stage of exploration.Many micromechanisms about spinel half-metals is still unknown,especially exploration of doping effect of rare-earth metals on the half-metallicity of Fe3O4is very limited.

In this paper,we will find out the doping effect of 6d transition rare-earth metals Ac and Th on the electronic structure and half-metallicity of Fe3O4by first principle and manage to predict new spinel half-metals with more excellent properties.

2 Model and method

As shown in Fig.1 is a 14-atom primitive cell of Fe3O4with two Fe atoms on A-sites and the other four on B-sites.Fe atoms were suitably doped by Ac or Th atoms with different concentration to form,namely,Fe1-xRexFe2-yReyO4(Re=Ac,Th;x=0,0.5,1;y=0,0.5,1.0,1.5,2.0).The subscript x represents the doping fraction of A-site Fe atoms while y B-site.

First principle calculation,also known as ab initio calculation,is based on the principles of quantum mechanism.It is mainly used to deal with the Hamilton equation,as shown in Eq.1.

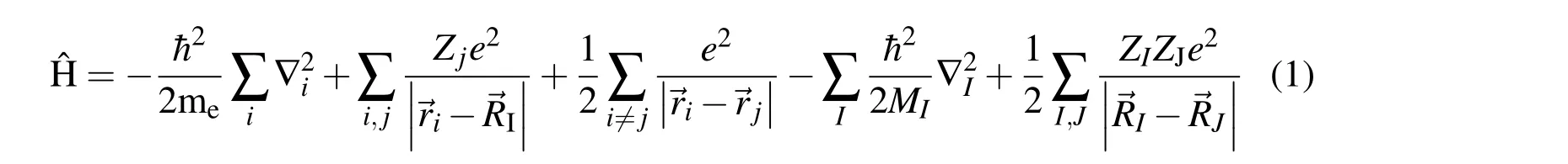
where on the right side of Eq.1,the parts from left to right represent the kinetic energy of electrons,the Coulomb potential energy between electrons and nucleus,interaction between electrons,kinetic energy of nucleus and Coulomb potential energy between nucleus,in which r and R represent the positions of the electron and nuclear respectively,Z the charge number of a nuclear,e the electronic charge,m and M the mass of the electron and nuclear.By self-consistent calculating electron motion and the interaction between electrons and nucleus,it can obtain the geometry structure,electronic,magnetic,thermodynamic properties of the materials[Kohn et al.(1965)].To solve this equation,we need to use some approximations.Based on the Born-Oppenheimer approximation[Born et al.(1954)],density functional theory(DFT)[Kohn et al.(1965)]was proposed in which the ground state physical properties of electrons,atoms and materials are all functionalized by electron densities and the energy function E[ρ]is minimized by the electron densityρ(r).Based on Hohenberg-Kohn principle[Hohenberg et al.(1964)],the Hamilton energy H is divided into three parts:kinetic energy T,interaction energy between electrons V and external electric field energy U,as shown in Eq.2

Figure 1:Primitive cell of Fe3O4.

Then with Φ presenting wave function the total energy function can be expressed as:

Kohn and Sham further derived this equation and by introducing electron exchange and correlation function Exc[ρ],the total energy function is expressed:

Kohn-Sham equation is derived as follows:

Finally the purpose of using DFT method to calculate the total energy of multiple electrons system and deal with charge density distribution is achieved.

We can see from Eq.6 that Exc[ρ]is the key for the accuracy of the calculating results.

Two approximation methods are used to treat Exc[ρ]:Local Density Approximation(LDA)and Generalized Gradient Approximation(GGA)[Kohnet al.(1965)].Electron density gradient is considered in GGA compared LDA,therefore,GGA is more suitable for treating systems with very large charge density fluctuation.Perdew-Wang 91(PW91)and Perdew-Burke-Ernzerhof(PBE)etc.are all the parameterized formation for GGA.

In this paper,the spin-polarized structural optimization,electronic structure and magnetic moments calculations were performed with the PBE parameterized GGA and projector augmented wave methods.The interaction between the valence electrons and ion cores were described by ultrasoft pseudo-potentials[Kresseet al.(1999)].The self-consistent calculations were performed with a 5×5×5 k-mesh and the cutoff energy of plane-wave expansion was 500eV.The relaxations of lattices were performed until the force on each atom was smaller than 0.03eV/Å,and all components of the stress tensor on the unit cell less than 0.05GPa.

3 Results and Discussion

To obtain the equilibrium lattice constant and determine the stable magnetic state of Fe1-xRexFe2-yReyO4(Re=Ac,Th;x=0,0.5,1;y=0,0.5,1.0,1.5,2.0),for each structure,structural optimizations were performed for the nonmagnetic(NM),ferromagnetic(FoM),ferrimagnetic(FiM)or antiferromagnetic(AFM)state.After optimization the structure of the lowest energy is believed to be stable with the corresponding lattice parameters and the corresponding magnetism.The electronic structure of the stable structure will then be calculated and their half-metallicity will also be determined.

3.1　Half-metallicity and Magnetic properties of Ac and Th doped Fe3 O4

Among these structures,besides Fe3O4,only AcFe2O4,FeAc2O4and ThFe2O4are calculated to be half-metallic materials.Population analysis of the resulting halfmetals is then performed using Mulliken formalism.Parameters listed in Table 1 are the equilibrium lattice constants and molecular(Ms)and atomic magnetic moments for Fe3O4,AcFe2O4,FeAc2O4and ThFe2O4within which MAmeans the A-site atom moment and MBthe B-site atom moment.Our calculated molecular magnetic moment of Fe3O4is 4.0µBat equilibrium lattice constant 5.94Å,agrees quite well with other’s[Liu,Chenetal.(2007)],which is4.0µBat5.935Å.And MAis-3.60µBwhile MBis 3.60µB,consistent with the reported characteristic that the A-site atoms have spin directions opposite to the B-site ones in Fe3O4,exhibiting ferromagnetic[Kimet al.(2007)],all conforming the accuracy of the method we used.In AcFe2O4,FeAc2O4and ThFe2O4,there are almost no spin moments for Ac and Th due to only one and two 6d electrons,respectively.But the Fe atom magnetic moments in AcFe2O4,FeAc2O4and ThFe2O4are 3.90,3.78 and 3.82µB,respectively,both slightly largerthan thatin Fe3O4.The impressive finding is that the calculated Msof AcFe2O4and ThFe2O4are 9.0µBand 8.1µB,much larger than that of Fe3O4.Higher magnetic molecule moment may cause stronger spin-correlation scattering for conductive electrons resulting in higher variation of resistance,and consequently obtaining higher magnetoresistance effects which is the key for spintronic devices.

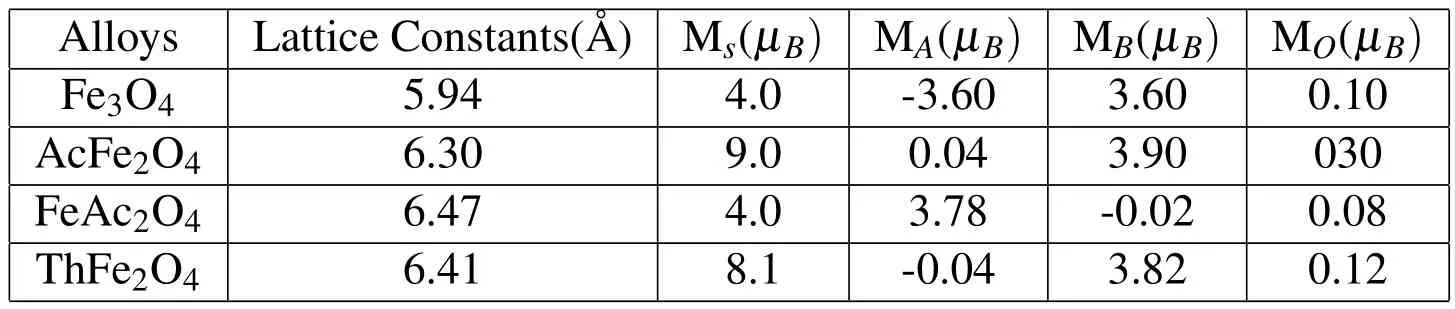
Table 1:Calculated lattice constants,molecular and atomic magnetic moments for Fe3O4,AcFe2O4,FeAc2O4 and ThFe2O4.

3.2　Electronic structure of AcFe2 O4 and ThFe2 O4

The total and partial spin-polarized density of states(DOS)of a)AcFe2O4and b)ThFe2O4are calculated and shown in Fig.2.We can see that there is much difference in DOS of up-spin and down-spin electrons near the Fermi energy level.Especially,at the Fermi level,the down-spin states cross the Fermi energy level,indicating a strong metallic nature of the spin-down electrons while the spin-up band structure exhibits a band gap indicating semiconducting nature.Therefore,our results reveal that AcFe2O4and ThFe2O4alloys exhibit half-metallic properties.The electrons are 100%spin-polarized for AcFe2O4and almost 100%for ThFe2O4.High spin polarization is the base for high sensitivity of spintronic devices considering magnetoresistance effects.So they are of great interest for scientific research and industrial applications.To show the electronic structures in detail,we plotted the down-spin energy bands of a)Fe3O4,b)AcFe2O4and c)down-spin and d)up-spin energy bands of ThFe2O4along high symmetry directions in the Brillouin zone in Fig.3.It is clear that the bottom of the conductance band touches the Fermi level at the G point but is rather weak,and the calculated spin-polarization for ThFe2O4is near 99%.Therefore,AcFe2O4and ThFe2O4are all considered to be typical II B-type half-metallic materials.Comparing the down-spin sub-bands of the three materials,we see that,there are some limited parabolas near the Fermi level meaning that electrons at the Fermi level are localized but not completely.And parabolas at both b)and c)are more clear than a),which means down-spin electrons of AcFe2O4and ThFe2O4at the Fermi level are less localized than that of Fe3O4.It is also seen that there is up-spin sub-bands in ThFe2O4.According to the two-fluid model of magnetoresistance effect,the up-spin and down-spin electrons transmit in parallel.So we believe that AcFe2O4and ThFe2O4both have higher conductivity than that of Fe3O4,and ThFe2O4has the highest.Higher conductivity is very important for the transmission of charges in half-metallic materials which plays a significant role in effective function.So AcFe2O4and ThFe2O4may be better than Fe3O4for spintronic devices.

We can see that for AcFe2O4and ThFe2O4in both majority and minority spin states,the total DOS are divided into bonding,nonbonding and antibonding states by an energy gap.The region from-7.2eV to-2.2eV corresponds to the bonding states,-1.8eV～0.9eV corresponds to the nonbonding states,states from 1.2eV to 6.3eV are associated with the antibonding states in AcFe2O4while the bonding,nonbonding and antibonding states of ThFe2O4are divided into-7.5eV～-2.4eV region,-2.1eV～0.7eV region and 0.9eV～3.6eV region.So the band region of AcFe2O4and ThFe2O4are about 13.5eV and 12.1eV,respectively which are very broad.The broad bands for AcFe2O4and ThFe2O4stem from their greater dependence on bonding-antibonding splitting and less on exchange splitting.And the large bonding-antibonding splitting is exactly the origin of the gap for AcFe2O4and ThFe2O4.

What’s more,for both AcFe2O4and ThFe2O4,the partial DOS of Fe shows a twopeak structure due to the strong hybridization between the Fe 3d states,Ac or Th 6d state and O 2p states caused by the crystal field effect.In upspin,the antibonding peak is below the Fermi level and occupied,but in down spin the splitting effect moves the antibonding peak high above the Fermi level.This distribution results in a large magnetic moment at Fe and makes Fe 3d electrons mostly responsible for the magnetization.The Fe 3d down-spin states cross the Fermi level,so they also have main contribution to the down-spin DOS atthe Fermilevel.The distribution of majority-and minority-spin of Ac or Th 6d and O 2p states are all nearly symmetry.So they make almost no contribution to the magnetization.As we have seen in Table1,the Fe spin moment is very large while the Ac,Th and O spin moments are all quite small.

Figure 2:Total and partial DOS of a)AcFe2O4and b)ThFe2O4 at their stable states,the dotted line represent the Fermi level.

Figure 3:The energy band structure for Fe3O4,AcFe2O4 and ThFe2O4,where the horizontal lines at 0 eV represent the Fermi energy level.

3.3　Half-metallicity of AcFe2 O4 and ThFe2 O4 under lattice distortion

Lattice distortion,mostly compression is often inevitably introduced in the production process and application,a small change of the lattice parameter may shiftEF(Fermi level)with respect to the half-metallic gap,which clearly affects the halfmetallicity as well as the transport properties.So it is necessary to consider the influence of lattice compression on half-metallicity.First,the lattice constants of the cells of Fe3O4,AcFe2O4and ThFe2O4are reduced by 0.05 Å which we consider as compressing condition.Geometry optimization was performed on the half-metal under compressing condition so that the optimized cell under compression was got.Then the magnetic properties and electronic character were performed and ana-lyzed.The changes of the molecular spin moments,spin-polarization of Fe3O4,AcFe2O4and ThFe2O4with lattice compression are presented in Fig.4.We can see that the spin-polarization of Fe3O4,AcFe2O4and ThFe2O4can maintain almost 100%up to 5.49 Å (-8%),6.10 Å (-3%)and 6.16 Å (-4%),respectively at which the molecular magnetic moments all witness a sudden decrease.Especially,ThFe2O4,when compressed to 6.21Å,its atomic spin moments all turn into zero,which means it lose the magnetism.That is because,as the lattice parameter is decreased,3d localization would become weaker,which can reduce the Fe spin moment.When it is decreased to a certain value,the atomic spin moments will be strongly reduced,resulting in significant magnetic losing.What is interestingis that in 5.49 Å～5.59 Å region,the magnetic properties of Fe3O4change significantly.A-site Fe spin changes from high and down into high and up while the B-site Fe spin becomes low and up from high and up,resulting in a 6µBmolecular magnetic moment compared to its 4.0µBat the equilibrium lattice constant.

Figure 4: Molecular magnetic moments and spin polarization rate for Fe3O4,AcFe2O4 and ThFe2O4 as a function of lattice parameter.

4 Conclusion

The half-metallicity and magnetroresistance of rare-earth metals Ac and Th doped Fe3O4are investigated using DFT method.Two better half-metallic candidates for spintronic devices,i.e.,AcFe2O4and ThFe2O4are predicted.Both of them are II B-type half-metallic materials at equilibrium lattice parameter 6.30 Å and 6.41 Å,respectively.Their molecular magnetic moments are calculated to be 8.1µBand 9.0µB,both are much larger than that of Fe3O4,i.e.,4.0µB.The large bondingantibonding splitting is believed to the origin of gaps for AcFe2O4and ThFe2O4.What’s more,the half-metallicity of AcFe2O4and ThFe2O4cannot be affected up to 3.0%and 4%compression,respectively,while that of Fe3O4can be maintained up to 8%compression.That is very important for application.

Acknowledgement:We would like to acknowledge the financial supports of the National Natural Science Foundation of China(21233010 and 11372104).This Project was granted financial support from China Postdoctoral Science Foundation(2012M520621/2013T60511).

Born,M.;Huang,K.(1954):Dynamical Theory of Crystal Lattices.London:Oxford University Press.

Chen,Z.H.;Li,J.B.;Li,S.S.(2012):First principles and Monte Carlo study of Mn-doped CuCl/CuBr as room-temperature ferromagnetism materials.J.Appl.Phys.,vol.111 no.6,pp.063913-1-063913-6.

Coey,J.M.D.;Venkatesan,M.(2002):Half-metallic ferromagnetism:Example of CrO2(invited).J.Appl.Phys.,vol.91,no.10,pp.8345-8350.

Dedkow,Y.S.;Rudiger,U.;Guntherodt,G.(2002):Evidence for the halfmetallic ferromagnetic state of Fe3O4by spin-resolved photoelectron spectroscopy.Phys.Rev.B,vol.65,no.6,pp.064417-064421.

De Groot,R.A.;Mueller,F.M.;Van Engen,P.G.;Buschow,K.H.J.(1983):New class of materials:half-metallic ferromagnets.Phys.Rev.Lett.,vol.50,no.25,pp.2024-2027.

Fong,C.Y.;Qian,M.C.;Pask,J.E.;Yang;L.H.;Dag,S.(2004):Electronic and magnetic properties of zinc blende half-metal superlattices.Appl.Phys.Lett.,vol.84,no.2,pp.239-241.

Hohenberg,P.;Kohn,W.(1964):Inhomogeneous Electron Gas.Phys.Rev.B,vol.136,no.3B,pp.B864-B871.

Hou,Y.H.;Zhao,Y.J.;Liu,Z.W.;Yu,H.Y.;Zhong,X.C.;Qiu,W.Q.(2011):First-principles investigations of Zn(Cd)doping effects on the electronic structure and magnetic properties of CoFe2O4.J.Appl.Phys.,vol.109,no.7,pp.07A502-1-07A502-3.

Kim,K.J.;Choi,S.;Lee,J.H.;Lee,H.J.;Park,J.Y.(2007):Variations of the electronic,optical and magnetic properties caused by V doping in magnetite thin films.J.Korean Phys.Soc.,vol.51,no.3,pp.1138-1142.

Kim,W.;Kawaguchi,K.;Koshizaki,N.;Mitsugu,S.;Tetsuro,M.(2003):Fabrication and magnetoresistance of tunnel junctions using half-metallic Fe3O4.J.Appl.Phys.,vol.93,no.10,pp.8032–8034.

Kohn,W.;Sham,L.J.(1965):Self-consistent equations including exchange and correlation effects.Phys.Rev.A,vol.140,no.4,pp.1133-1138.

Kopcewicz,M.;Stobiecki,F.;Jagielski,J.;Szymanski,B.;Urbaniak,M.;Lucinski,T.(2005):Modification of microstructure and magnetic properties of Fe/Cr multilayers caused by ion irradiation.J.Magn.Magn.Mater.,vol.286,pp.437–441.

Kresse,G.;Joubert,D.(1999):From ultrasoft pseudopotentials to the projector augmented-wave method.Phys.Rev.B,vol.59,no.3,pp.1758-1775.

Liu,J.;Chen,X.M.;Liu,Y.;Dong,H.N.(2007):First principle calculation on electronic and magnetic properties of new half-metal TiFe2O4.Phys.Scr.,vol.T129,pp.144–148.

Liu,J.;Chen,X.M.;Liu,Y.;Dong,H.N.(2008):Electric and magnetic properties of new rare-earth half-metal LiPr2O4.Solid State Ionics,vol.179,pp.881–886.

Liu,J.Wang,X.Q.;Liu,Y.;Dong,H.N.(2007):First principle calculation of electric and magnetic properties for new half-metal Fe2ScO4.Chin.J.Chem.Phys.vol.20,no.3,pp.291-295.

Ming,X.;Wang,X.L.;Du,F.;Han,B.;Wang,C.Z.;Chen,G.(2012):Unusual intermediate spin Fe3+ion in antiferromagnetic Li3FeN2.J.Appl.Phys.,vol.111,no.6,pp.063704-1-063704-6.

Prinz,G.A.(1999):Magnetoelectronics.Science,vol.282,no.5394,pp.1660-1663.

Tan,C.L.;Huang,Y.W.;Tian,X.H.;Jiang,J.X.;Cai,W.(2012):Origin of magnetic properties and martensitic transformation of Ni-Mn-In magnetic shape memory alloys.Appl.Phys.Lett.,vol.100,no.13,pp.132402-1-132402-4.

Wolf,S.A.;Acoschalom,D.D.;Buhrmanm R.A.;Daughton,J.M.;von Molnár,S.;Roukes,M.L.(2001):Spintronics:a spin based electronics vision for future.Science,vol.294,no.5546,pp.1488–1495.

Yao,Q.W.;Kimura,H.;Wang,X.L.;Konstantinov,K.;Zhao,H.Y.;Qiu,H.(2012):Density of states,magnetic and transport properties of Nd doped two dimensional perovskite compound Sr2CoO4.J.Appl.Phys.,vol.111,no.7,pp.07D708-1-07D708-3.

Zhao,Y.H.;Li,Y.F.;Liu,Y.(2012):Half-metallic p-electron ferromagnetism in alkaline earth doped AlAs:A first-principles calculation.Appl.Phys.Lett.,vol.100,no.9,pp,092407-1-092407-3.