A Novel Approach to Identify the Thermal Conductivities of a Thin Anisotropic Medium by the Boundary Element Method

Y.C.Shiah,Y.M.Lee and T.C.Huang

1 Introduction

Since the 1970s’,anisotropic materials have been extensively applied in engineering for various purposes.With the rapid evolvement of nanotechnologies,new materials have been developed using carbon nanotubes(CNTs),whose thickness is approximately 50,000 times thinner than a human hair.Due to their extraordinary thermal conductivity and mechanical properties,CNTs find applications as additives to various applications.Very recently,the study of buckypaper,a thin sheet originally fabricated to handle CNTs,has attracted significant research[e.g.Wang et al(2004);Biercuk et al(2002);Schadler et al(1998);Ajayan et al(2000);Lozano et al(2001);Rosen and Jin(2002)]owing to its promise in various applications,such as armors,next-generation electronics and displays,etc.However,the experimental study of its properties has been only limited to the in-plane characteristics due to the difficulty of measuring data in the transverse direction.For any other thin anisotropic medium,this difficulty always exists,especially for the properties associated with cross-terms.The simplest way to avoid this would be to assume transversely isotropy,where the cross-terms disappear;however,this simplification would introduce errors to a certain degree.

In this paper,an inverse analysis based on the BEM is proposed to serve as an auxiliary means for measuring the thermal conductivities of an ultra-thin anisotropic medium.Basically,the idea is to sandwich the unknown anisotropic medium as the core(Fig.1)between isotropic materials with known conductivities.

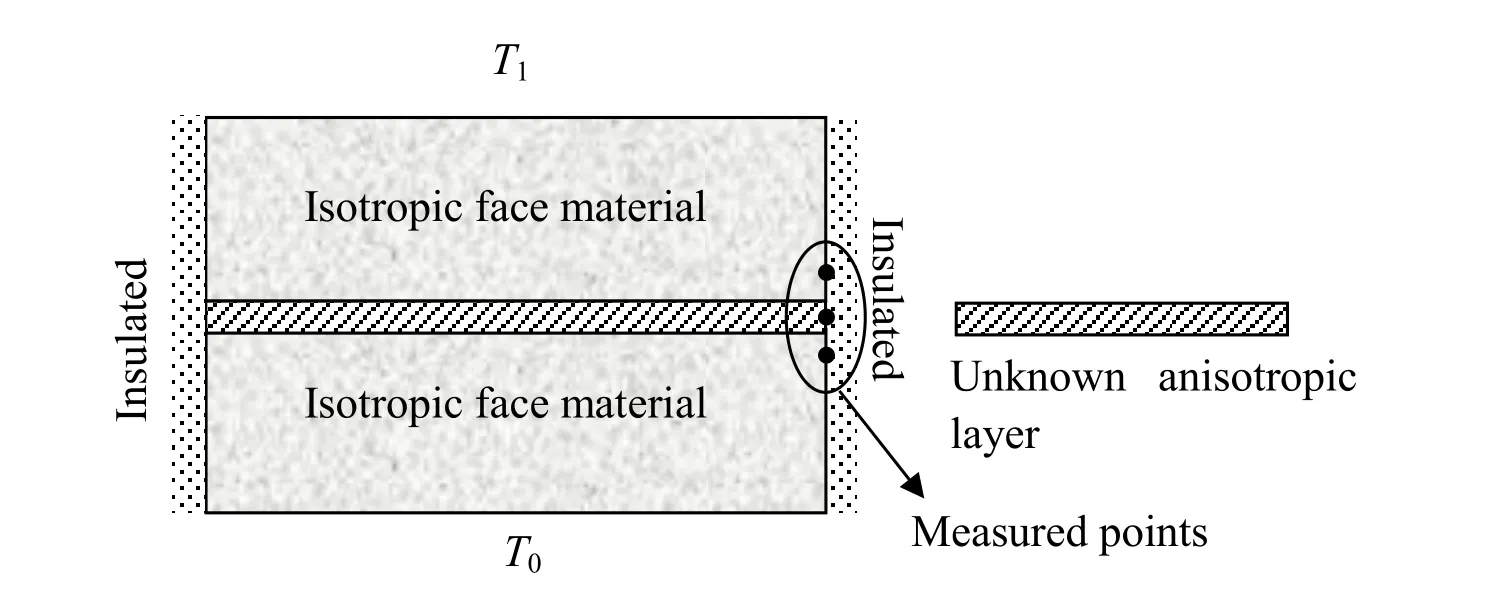
Figure 1:An integrated composite subjected to a heat flux.

For the ease of analysis,the top and bottom sandwiching materials are chosen to be the same.With proper boundary conditions specified,the generally anisotropic conductivities of the core layer are inversely determined by the temperature data measured in the neighborhood of the sandwiched medium.For the present inverse analysis,the boundary element method is employed.In contrast with the domain solution techniques such as the finite element method(FEM)and the finite difference method,the BEM is renowned for its distinctive feature that only the boundary needs to be modeled.This feature is especially ideal for the inverse analysis since only boundary data can be measured from experiments.Early inverse analysis may be traced back to treat problems of thermal conduction by Shumakov(1957).Since then,the inverse study on the thermal conduction problems has been extensively applied to various identifications of initial conditions,boundary conditions,geo-metric parameters,and heat sources,etc.Among these works,Sparrow et al(1964)studied the inverse problem of transient heat conduction by applying the technique of Laplace Transform and the Integral method.After that,lots of works have been published for the inverse analysis of thermal problems.To name a few as examples,Alifanov(1974)introduced a concept of iteration by gradients for inversely analyzing the heat conduction problem.Based on the perturbation principle,the CGM has been widely applied to various inverse problems[Huang and Wu(1995a,1995b);Huang and Yan(1995)].As aforementioned,owing to its distinctive notion of boundary discretization,it is beneficial to apply the BEM to inverse problems[e.g.Martin and Dulikavich(1998);Hematiyan et al(2012)].For this,the inverse analysis based on the BEM has been rapidly growing in recent decades,especially for problems of thermal conduction.For example,Pasquetti and Petit(1994)made use of the time-dependence with space to inversely investigate the transient temperature field at corners using the BEM.Mellings and Aliabadi(1993)employed the Dual boundary element for studying inverse potential problems in crack identification.Wei and Li(2009)used the approach of generalized cross validation to perform an inverse analysis of heat conduction in multilayer domain.Using the BEM and the singular value decomposition,Lagier et al(2004)presented a numerical solution to the linear multidimensional unsteady inverse heat conduction problem.There are too many to mention all as a complete review for the works on the BEM’s applications in various inverse analyses pertinent to thermal conduction.For more references as examples,one may refer to references[Pasquetti and Petit(1994);Zed et al(2000);Singh and Tanaka(2001);Hon and Wei(2004);Sladek et al(2006);Dong et al(2007);Onyango et al(2009);Movahedian et al(2013)].

As the prelude for the inverse analysis of 3D anisotropic elasticity[Shiah et al(2012)],the present work is to identify the thermal conductivities of an ultra-thin layer of 2D generally anisotropic medium by the inverse analysis of CGM based on the BEM.For facilitating experimental setups to measure temperature data,the ultra-thin layer is sandwiched in isotropic materials(e.g.epoxy resin on both sides)as an integrated multi-domain.As has been reported in the BEM literature,nearsingularities will appear in the integral equation for treating the ultra-thin layer.Very recently,the leading author has applied the scheme of integration by parts to regularize the boundary integrals for 3D anisotropic heat conduction[Shiah et al(2013)].The present work employs the scheme of integration by parts(IBP)[Shiah and Shi(2006)]for modeling the thin layer and employs the direct domain mapping technique[Shiah and Tan(1997)]to treat its anisotropy.For the inverse analysis,the CGM is applied,where the temperature field on the boundary near the core is provided as the target function to be satisfied.For verification,numerical examples are provided at the end.

2 BEM treatment of the heat conduction

For elucidating how the BEM is applied to the inverse analysis,a brief review of the fundamentals is provided fist.As shown in Fig.1,consider an integrated composite consisting of three layers-two face layers of the same isotropic material on its top and bottom plus one thin anisotropic layer sandwiched between as the core.For the generally anisotropic layer in 2D,the governing Euler’s equation is written as

where,T stands for the temperature change,and Kij are the thermal conductivities coefficients defined in the x1-x2 coordinate system.From thermodynamic considerations and Onsagar’s reciprocity relation,the coefficients Kij must satisfy

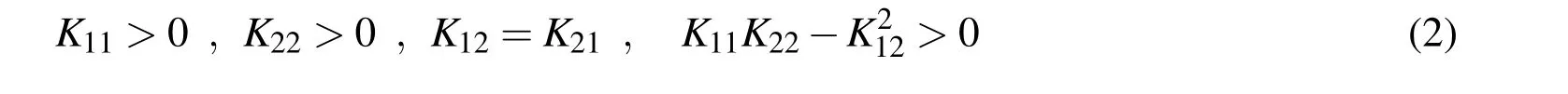
The analysis can be significantly simplified in the case of orthotropy,where the cross-derivative terms are absent.As a result,a commonly adopted approach to numerically treat the fully anisotropic problem is,first,to determine the principal axes(ζ1,ζ2)by rotating the original Cartesian axes such that the cross-derivative terms will disappear.Another attractive approach to treat the anisotropic problem is to employ a coordinate transformation such that T in the transformed domain is governed by the standard Laplace’s equation.This was studied analytically by but with limited success.The difficulties in this analytical approach are due to the complexities that stem from the distorted boundary in the mapped plane.In their efforts to formulate an exact transformation of the volume integral associated with the thermal effects into surface integrals for plane anisotropic thermoelasticity in BEM,Shiah and Tan(1997)also developed a similar transformation and applied it to numerically treat the two-dimensional anisotropic problem in the BEM field theory.The main advantage of such BEM treatment lies in the fact that the anisotropic field problem can be easily solved using any readily available BEM codes for‘isotropic’potential theory with relatively minor program modifications.The linear transformation/inverse transformation takes the following form,

where[F(Kij)]is the transformation(and[F-1(Kij)]the inverse transformation)matrix,given by

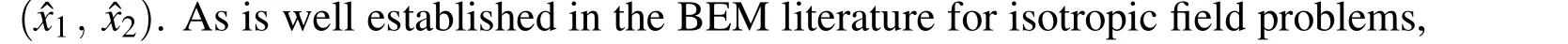
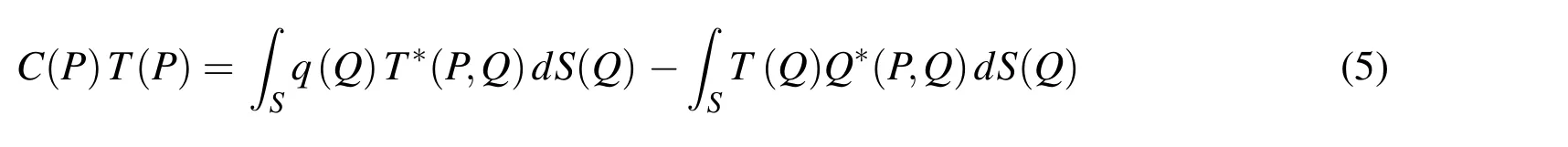
wherePandQare the source and field points on the boundary,respectively,C(P)are coefficients dependent of the geometry at the source point,and T*(P,Q)andQ*(P,Q)represent the fundamental solutions for the temperature and its normal gradient,given by

In Eq.(6),ris the distance between the source pointPand the field pointQon the element under integration.To numerically solve the boundary integral equation(BIE)of Eq.(5),the boundary surface is discretised into a number of segments or elements,sayMelements,with a total ofNnodes.Following the usual interpolation process for n-order elements,one may have nodal values of coordinates,temperature,and temperature gradients expressed in terms of the local coordinateξ∈[-1,1]as

whereN care the shape functions whose quadratic forms are expressed as

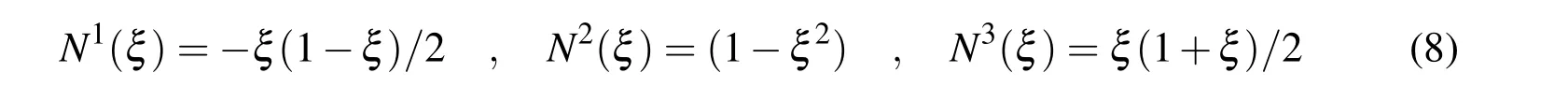
In convenience of later derivations,the quadratic shape function can be expressed as

whereαc,βc,γcare constant coefficients.Substitution of Eqs.(6),(7)into Eq.(1)results in the discretised BIE form,

where the superscriptarepresents thea-th global node of the boundary mesh,bdenotes theb-th element,andcisc-th node of the element.Also in Eq.(10),J(ξ)is the Jacobian transformation of the path from the global coordinates to the local coordinateξ.Sequentially,the collocation process via Eq.(10)forms a set ofNlinear algebraic equations for the unknown temperature and temperature gradients at the boundary nodes,which can be solved by,for example,the Gaussian elimination scheme.For treating the multi-domain as shown in Fig.1,the conventional sub-regioning technique in the BEM can be applied;however,proper interfacial conditions must be specified.

With the presence of an anisotropic medium sandwiched in the composite,the interfaces consider the isotropic/anisotropic conditions,including the continuity and the equilibrium between adjacent interfaces.The former states that the temperature of contiguous surfaces must be identical between the isotropic material(1)and the anisotropic material(2),i.e.

Since the temperature field does not depend on the coordinate transformation,Eq.(11)must hold true even though the distorted interface of the anisotropic medium may misalign with that of the isotropic one.However,due to the misalignment of the unit outward normal on the interface of the anisotropic material,the equilibrium condition needs to be reformulated accordingly.For this purpose,consider first the heat fluxes out of the interfaces between adjacent materials 1(isotropic)and 2(anisotropic)in the physical plane.The thermal equilibrium between the interfaces states that the sum of the normal heat fluxes across their interfaces shall vanish,i.e.

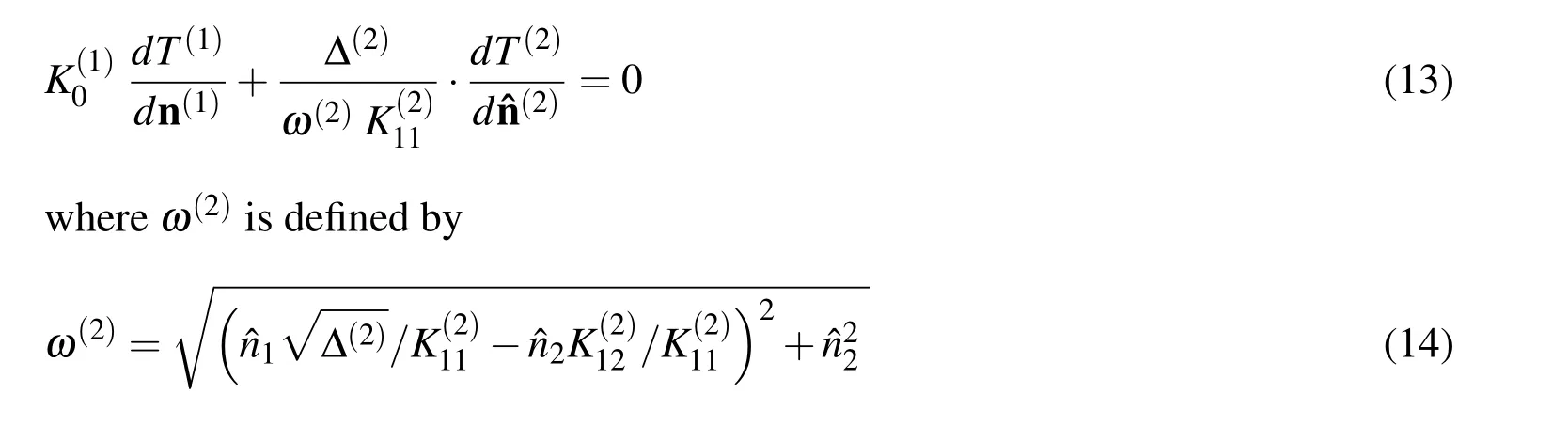
Asa resultofapplying Eq.(11)and Eq.(13)to the sub-regioning scheme in the BEM for providing additional equations,all boundary known values can be determined by solving the BIE for the both materials.However,there is still another issue needed to be dealt with for the sandwiched material,namely the near-singularity.It is seen that for an ultra-thin layer,the source pointPshall approach the integration element.Thus,it is evident that regular numerical integration schemes will fail to evaluate the nearly singular integrals accurately.To resolve the problem,these integrals need to be regularized by the processes to be described next.

3 Regularization of integrals

As reported in the BEM literature,numerical difficulties will arise for evaluation of the integrals when the source point approaches the element under integration.In principal,this happens to the case when the distance from the source point P to its projection point on the element is one-order less than the characteristic size of the element.Obviously,such a process needs to be taken for treating the anisotropic core layer due to its ultra-small thickness in the transverse direction.Although this issue may be directly resolved by subdividing the element into several small intervals with each interval length of the same order as the distance,this scheme is not generally feasible since overloading computation will be incurred due to excessive subdivisions for ultra thin structures.Thus,an appealing way of dealing with this problem is to regularize the nearly singular integrals such that the usual numerical schemes,like Gauss quadrature scheme for example,may yield accurate results.

The presentanalysisconsidersthe mostgeneralcase when quadratic elements(c=3)are employed;however,it should be bear in mind that the formulations used can be easily extended for general high-ordered elements.From Eq.(10),the first integral reveals weak singularity.For quadratic elements,the weakly singular integral is expressed as

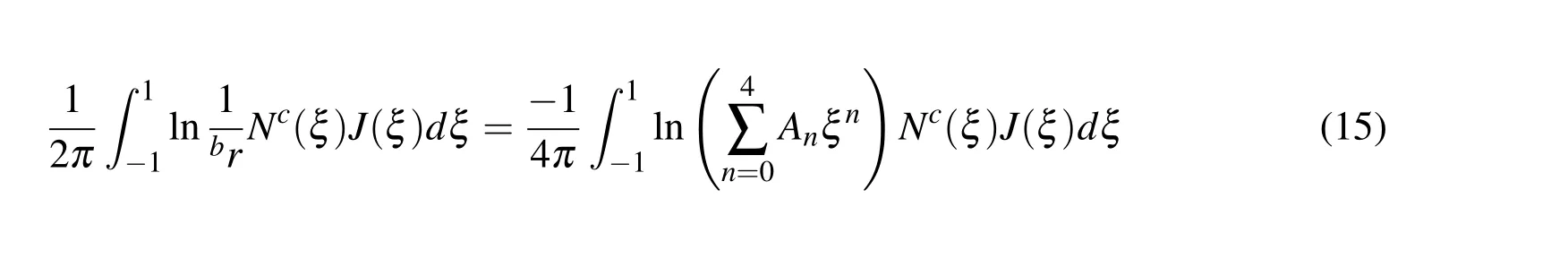
In the above equation,the JacobianJ(ξ)is given by

where the invariantsB0,C0,andD0are defined by the followings:

and the invariantsA0～A4are given by

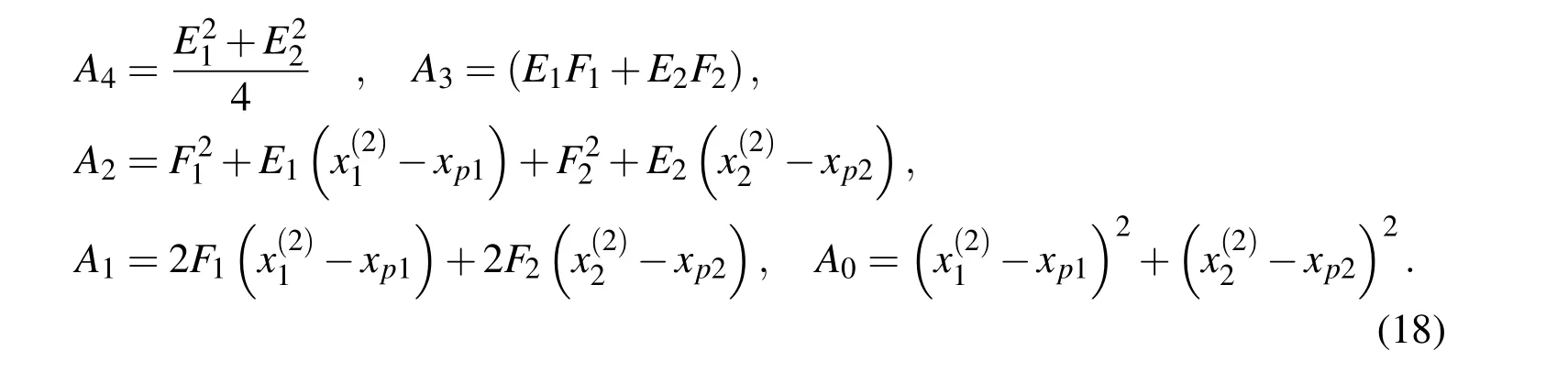
By rewriting the 4-degree polynomial in the logarithmic function in terms of its quadruple rootsRi,one may obtains

In fact,the rootsRican be numerically determined by any root-finding schemes without difficulties.As a result of applying the scheme of integration by parts proposed by Shiah and Shi(2006),the weakly singular integral is given by

where the function Ω(ξ)is defined as

Obviously,the integrand on the right hand side of Eq.(20)is completely free of singularity due to the fact that whenξapproaches to one of the rootsRi,the integrand will converge rapidly.Thus,the regularized form of the integral can be integrated using any conventional numerical schemes without any difficulty.However,special care must be taken for treating the degenerated case of straight elements whenA4vanishes.

For geometrically linear elements,it can be readily shown that the Jacobian is expressed as

By following the previous treatment,the integral is rewritten as

whereRiare defined by

Apparently,Eq.(24)may be analytically integrated to give

whereN′c(ξ)represents the first order differentiation of the shape function;Ω1(ξ)～Ω3(ξ)are defined by

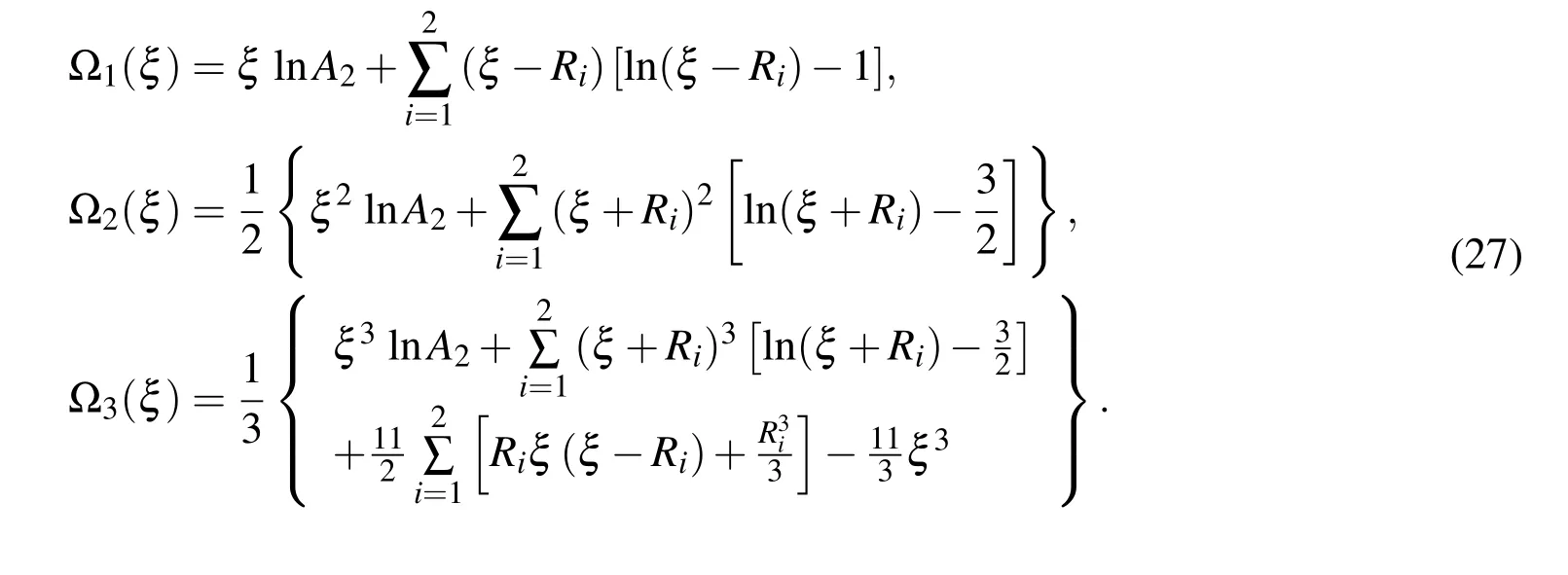
Next,the similar processes can also be taken for treating the strongly singular integral in Eq.(10).Making use of the standard quadratic interpolation,one may immediately obtain

where the invariantsC0～C2are defined by

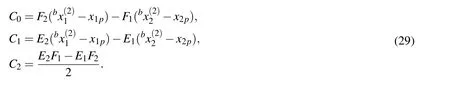
As a result of performing analytical integration,one obtains

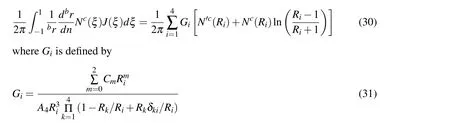
and theδkiis the kronecker delta defined as usual.Likewise,the special treatment of the degenerate case is needed,where bothA3andA4will vanish.In that case,the integral becomes

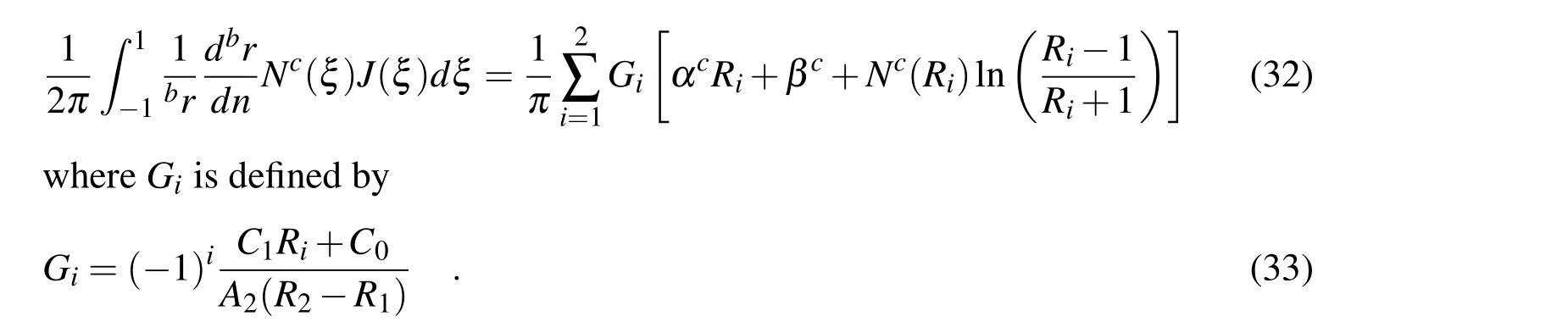
For the special case when repeated double roots occur(i.e.R2=R1=R),Eq.(32)becomes

whereH c(R)is defined by

4 Inverse analysis of the Kij of the core layer

The goal of the present analysis is to identify the generally anisotropic conductivities of the ultra-thin core layer by use of the temperature data measured on a few boundary points as indicated in Fig.1.For easy preparation of the composite sample,epoxy is an ideal candidate to serve as the sandwiching material,whose average conductivity value is aboutK0=0.541 W/m-0K By assumption,the epoxy is adopted to be the face material and the unknown anisotropic core layer has the following conductivity coefficients,

For illustration of how the inverse analysis is carried out,the boundary conditions consider the top and bottom surfaces subjected to 1000Cand 00C,respectively,while the opposite vertical sides are thermally insulated.Of no doubt,the heat conduction in the multiply adjoined composite can be analyzed using the BEM as described previously.The inverse analysis will take the conductivities of the core layer as unknowns and uses a few temperature data taken from the boundary points on the insulated surface as shown in Fig.1.Before performing the inverse analysis,the problem is analyzed forwardly with its dimensions and the BEM mesh described in Fig.2.

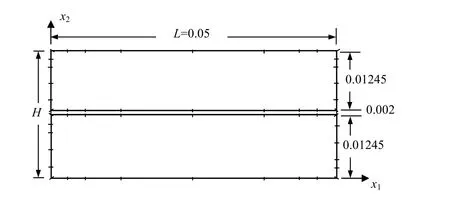
Figure 2:BEM modeling of the composite.

For verification,this forward problem is also investigated using ANSYS,a commercial FEM-based software package,to provide a comparison platform.It should be noted that on purpose,the thickness of the core layer is designed to have a thickness that the ANSYS may handle in a reasonable period of time.For much smaller thicknesses that require much refined meshes,overwhelming FEM mesh discretization may lead to quite heavy computational burdens.In fact,the CPU-time of the present BEM analysis took only 3.12×10-2(seconds)by an Intel-I7 PC,while the complete run of the ANSYS took 13.46(seconds)by the same machine.One may consider this not to be a significant issue for simply a forward analysis;however,for the inverse analysis requiring more than sounds of iterations,this will be an obvious advantage to employ the BEM for saving the computation costs.Figure 3 and Figure 4 show the normalized temperature distribution on the interfaces and the insulated surfaces,respectively,where the normalization factor∆T=1000Cis used.From the comparisons shown in the both plots,the excellent agreements between the both results can be observed.

Figure 3:Temperature distribution on interfaces.

Next,consider the inverse problem when the conductivities of the anisotropic core layer are taken to be unknowns.For this problem,the temperature field can be only measured on the boundary.As can be seen from Fig.3 and Fig.4,one may take either interface points or a few boundary points on the insulated surfaces near the core for characterizing the temperature response.For experimentally recording temperature on the interfaces,thermal couples need to be fixed onto the interfaces during the curing process of the epoxy resin.Apparently,it is much easier to take data from the insulated surfaces due to the accessibility of measured positions and repeatability of measurements.For the process of the inverse analysis,let the target function be

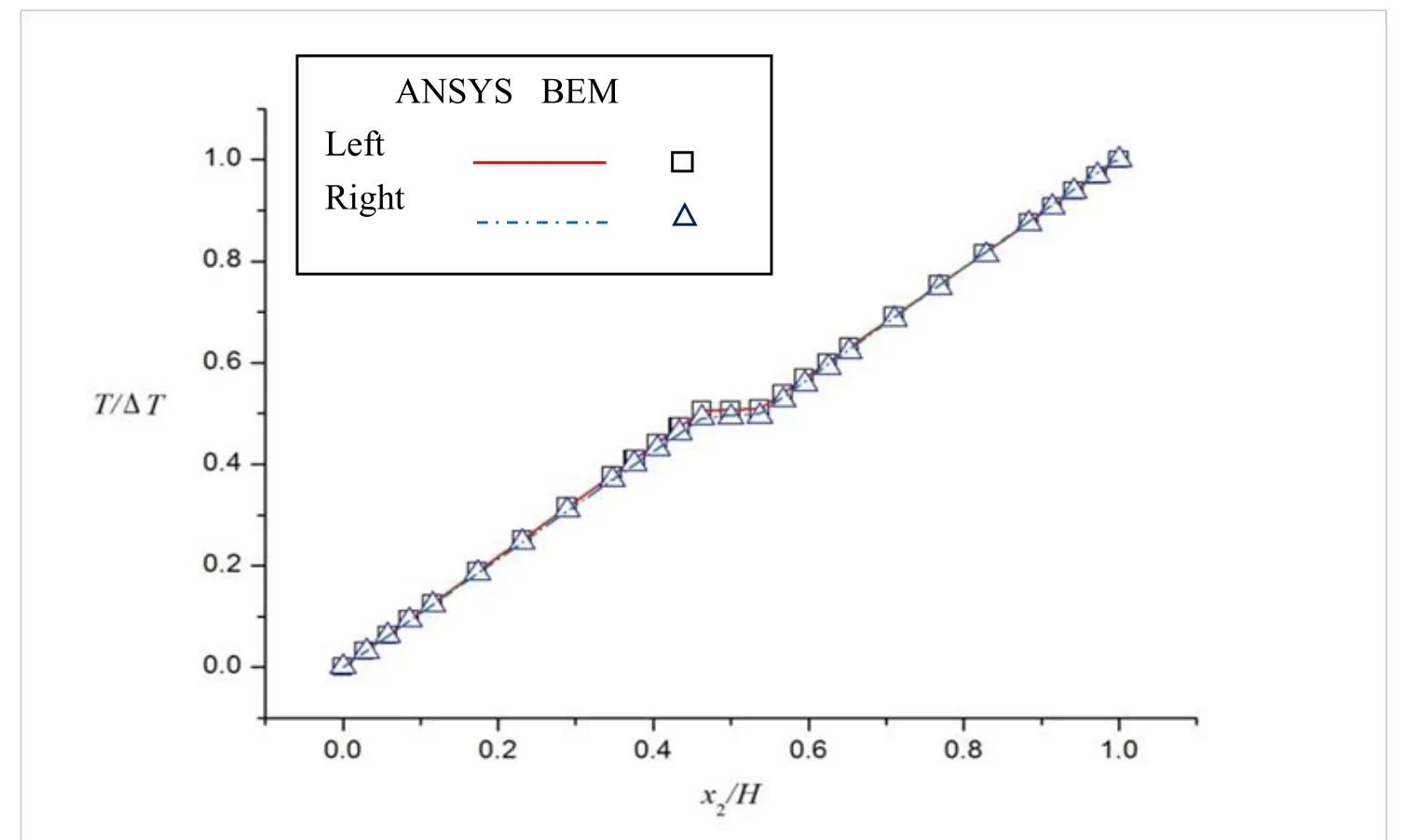
Figure 4:Temperature distribution on insulated surface.

In the above equation,the partial differentiations are taken using the central difference scheme,namely

鲁迅在儿童文学翻译作品的选材上没有选择格林、安徒生、王尔德等，而是选择了爱罗先珂、望.霭覃等。这固然与鲁迅喜欢独辟蹊径有关，但是，这种选材无疑发自内心。鲁迅在儿童文学翻译上关注个性与博爱、童心、童趣其次非常重视儿童话语权。(秦弓，2004)[6]他的翻译作品中多以白话文为主，所以他主张直译。鲁迅的翻译也启迪了其儿童文学创作，如《社戏》、《鸭的喜剧》、《兔和猫》等。

where∆fis a small difference step,chosen to be 10-4for the present analysis.For the initial iteration(t=0),the first searching ofS(0)is along the negative direction at its initial guess point,i.e.

(Step 4):Calculate the following ratio of gradients,

(Step 5):Determine the next searching direction by

As a matter of fact,the required iteration number strongly depends on the selection of initial guessed values.For investigating how the initial settings affect the iteration number,numerical experiments were performed for various tries of the initial values by

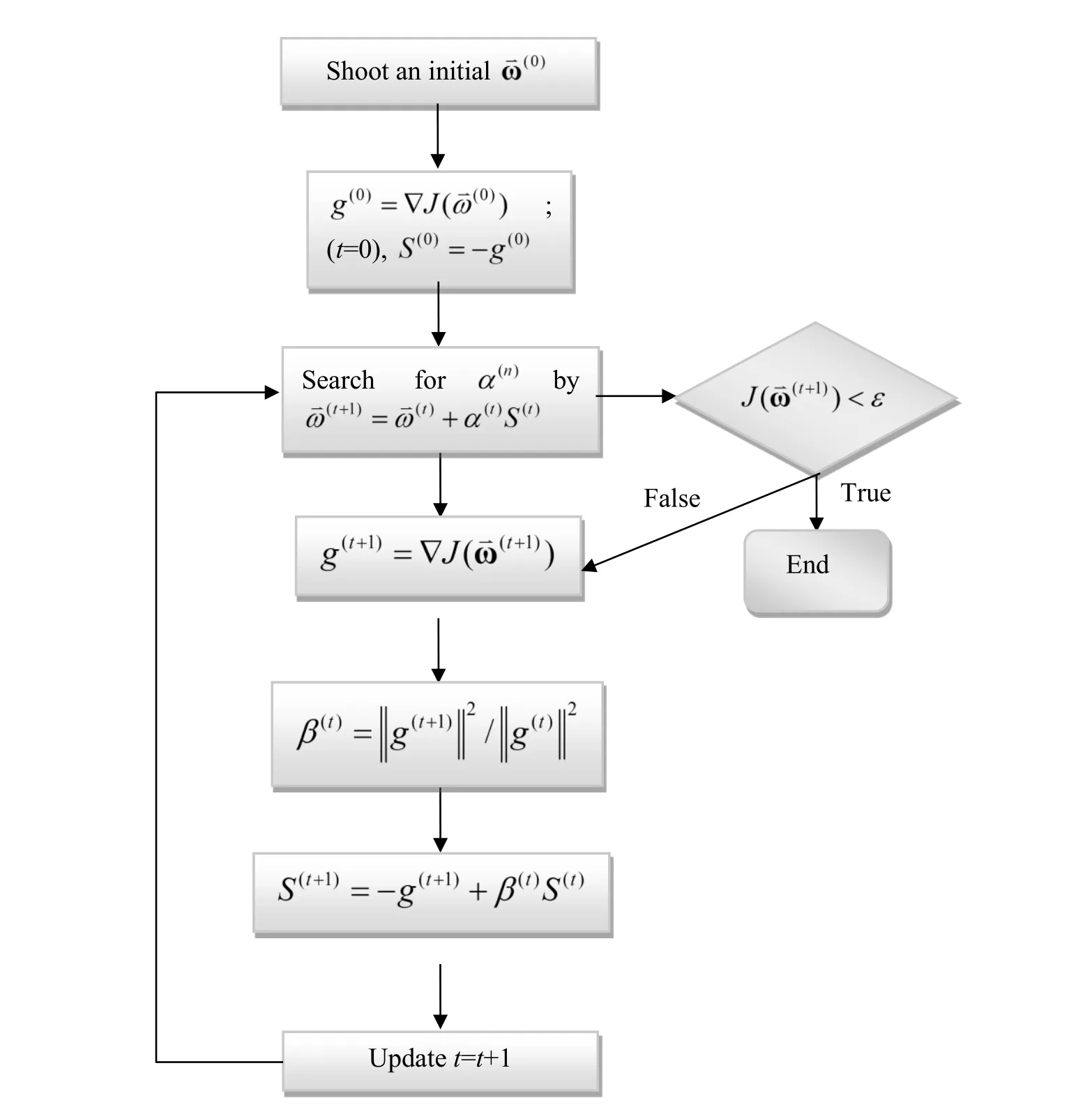
Figure 5:Flowchart of the inverse analysis by the CGM.

For the experiments,the test was to find the best m and n that gave the least iterations.For the present analyses,11 nodes on the right surface near the core layer were selected as the sample points for collecting temperature data.Figures 6-12 display the required iteration numbers and percentages of errors varied with n for various m.From these plots,it can be observed that form＜1,there is a trend of declining numbers of iterations for greatern.Also,from Fig.4,an obvious conclusion may be drawn that the optimum condition occurs atn=0/m=4.Another interesting issue worthy of investigations is the choice of sample points for collecting temperature data.For this,the inverse analyses using the optimum condition ofn=0/m=4 were also carried out for selecting 11 sample points particularly on the left surface and for another case when 22 points were selected on both left/right surfaces as the sample points.The results showed that the selection of 22 points on both sides required the least iteration number.The comparison of the required numbers of iterations is shown in Fig.13.However,considering that fact that no significant reduction of the iteration numbers(10%at most)was present and more measured data would be required,the authors suggest to employ the one-side approach,in-volving less measurements of temperature data.By using the optimum condition of n=0/m=4 and adopting the one-side approach,all calculated conductivities are tabulated in Tab.1,where the percentages of errors are also listed.From the comparison,it can be clearly seen that the inverse BEM analyses are very accurate in identifying the thermal conductivities of the anisotropic core layer.

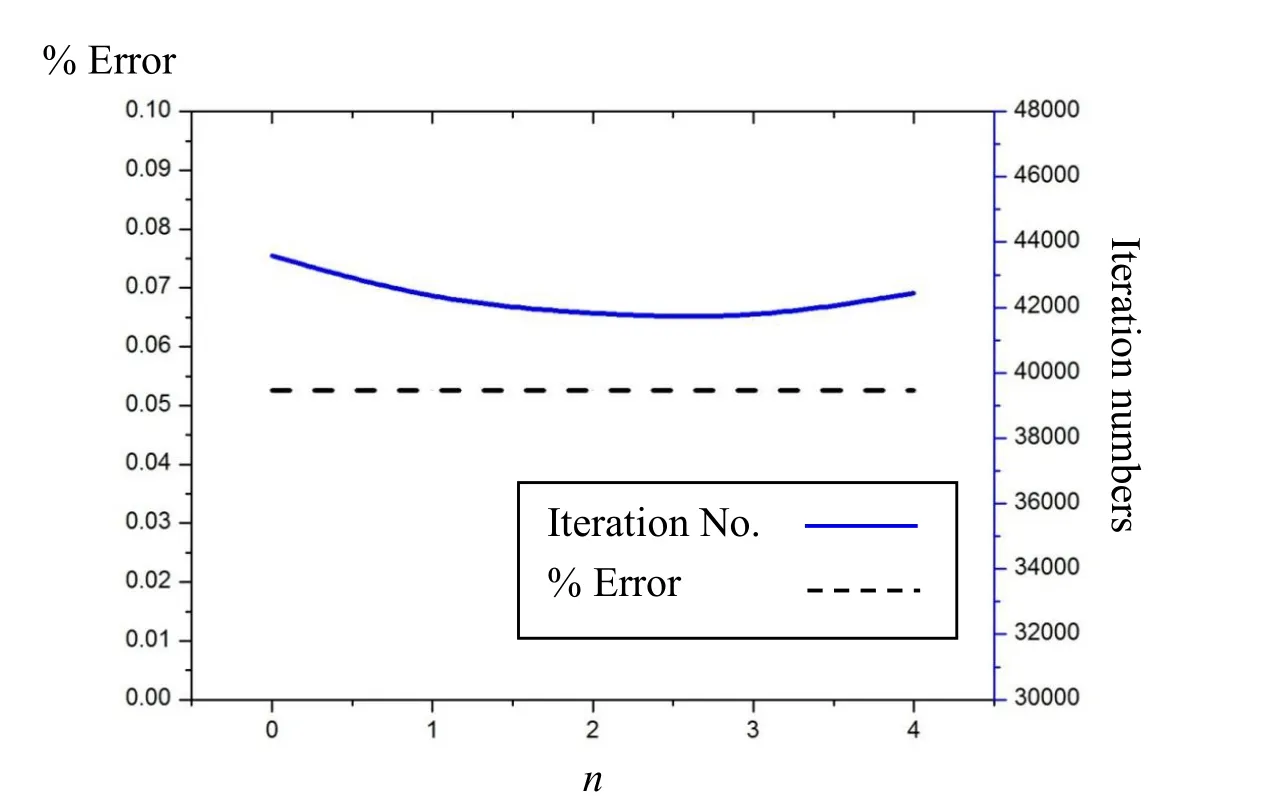
Figure 6:Variations of the iteration numbers&error percentages for m=1.

Figure 7:Variations of the iteration numbers&error percentages for m=2.

Figure 8:Variations of the iteration numbers&error percentages for m=3.

Figure 9:Variations of the iteration numbers&error percentages for m=4.

Figure 10:Variations of the iteration numbers&error percentages for m=1/2.

Figure 11:Variations of the iteration numbers&error percentages for m=1/3.

Figure 12:Variations of the iteration numbers&error percentages for m=1/4.

Figure 13:Required iteration numbers for distinct selections of sample points.

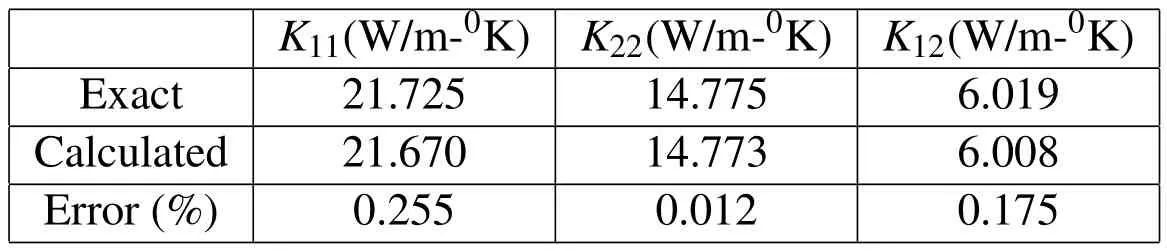
Table 1:Comparison between the calculated thermal conductivities and the exact values.

5 Conclusive remarks

With the rapid march of new technologies,new anisotropic materials have been developed.It is quite often that they are subtle engineered to thin layers to meet various purposes of design.So,for implementing the thin materials in practice,it is crucial to characterize their various properties either by experiments or with numerically modeling.For resolving the difficulty of measuring transverse properties,this paper presents a novel approach to identify the thermal conductivities of a thin generally anisotropic layer by the BEM inverse analysis.For the ease of experimental measurements,the thin layer is sandwiched between two isotropic face materials,whose thermal conductivities are known.By providing the measured temperature on the insulated surface,the anisotropic thermal conductivities of the core layer are calculated using the inverse BEM analysis combined with the CGM approach.The calculated results showed that the temperature measurements on simply one side of the composite would be sufficient to yield accurate results,yet with trivial sacrifice of 10%more iterations involved at most.Owing to less data to take,this one-side approach is ideal for the identification purpose in practice.From the numerical experiments,this approach of inverse BEM analysis has shown great computational efficiency and accuracy.Particularly,this approach is ideal for identifying the mechanical properties of the anisotropic thin layer since experimental measurements in the transverse direction are unlikely for the small thickness.With the shown promise of implementation,this approach can be applied to identify the elastic and thermoelastic properties,such as the stiffness and thermal expansion coefficients,of generally anisotropic thin media.

Acknowledgement:The authors gratefully acknowledge the financial support for this work from the National Science Council of Taiwan(NSC 102-2221-E-006-290-MY3).

Ajayan,P.M.;Schadler,L.S.;Giannaris,C.;Rubio,A.(2000):Single-walled carbonnanotube–polymer composites:strength and weakness.Adv Mater,vol.12,issue 10,pp.750-753.

Alifanov,O.M.(1974):Solution of an inverse problem of heat conduction by iteration methods.J.of Eng.Phys.,vol.26,issue 4,pp.471-476.

Biercuk,M.J.;Llaguno,M.C.;Radosavljevic,M.;Hyun,J.K.;Johnson,A.T.;Fischer,J.E.(2002):Carbon nanotube composites for thermal management.Appl Phys Lett;vol.80,issue 15,pp.2767-2769.

Dong,C.F.;Sun,F.Y.;Meng,B.Q.(2007):A method of fundamental solutions for inverse heat conduction problems in an anisotropic medium.Engineering Analysis with Boundary Elements,vol.31,issue 1,pp.75-82.

Hematiyan,M.R.;Khosravifard,A.;Shiah,Y.C.;Tan,C.L.(2012):Identification of material parameters of two-dimensional anisotropic bodies using an inverse multi-loading boundary element technique.CMES-Computer Modeling in Engineering&Sciences,vol.87,no.1,pp.55-76.

Hon,Y.C.;Wei,T.(2004):A fundamental solution method for inverse heat conduction problem.Engineering Analysis with Boundary Elements,vol.28,issue 5,pp.489-495.

Huang,C.H.;Wu,J.Y.(1995a):An inverse problem of determining two boundary heat fluxes in unsteady heat conduction of thick-walled circular cylinder.Inverse Problems in Engineering,vol.1,issue 2,pp.133-151.

Huang,C.H.;Wu,J.Y.(1995b):Function estimation in predicting temperaturedependent thermal conductivity without internal measurements.J.of Thermophysics and Heat Transfer,vol.9,issue 4,pp.667-673.

Huang,C.H.;Yan,J.Y.(1995):An inverse problem in simultaneously measuring temperature-dependent thermal conductivity and heat capacity.Int.J.Heat Mass Transfer,vol.38,issue 18,pp.3433-3441.

Lagier,G.L.;Lemonnier,H.;Coutris,N.(2004):A numerical solution of the linear multidimensional unsteady inverse heat conduction problem with the boundary element method and the singular value decomposition.International Journal of Thermal Sciences,vol.43,issue 2,pp.145-155.

Lozano,K.;Rios,J.;Barrera,E.V.(2001):A study on nanofiber-reinforced thermoplastic composites(II):investigation of the mixing rheology and conduction properties.J Appl Polym Sci.,vol.80,issue 8,pp.1162-1172.

Martin,T.J.;Dulikavich,G.S.(1998):Inverse determination of steady heat convection coefficient distributions.ASME J.of Heat Transfer,vol.120,pp.328-334.

Mellings,S.C.;Aliabadi.M.H.(1993):Dual boundary element formulation for inverse potential problems in crack identification.Engineering Analysis with Boundary Elements,vol.12,issue 4,pp.275-281.

Movahedian,B.;Boroomand,B.;Soghrati,S.(2013):A Trefftz method in space and time using exponential basis functions:Application to direct and inverse heat conduction problems.Engineering Analysis with Boundary Elements,vol.37,issue 5,pp.868-883.

Onyango,T.T.M.;Ingham,D.B.;Lesnic,D.(2009):Reconstruction of boundary condition laws in heat conduction using the boundary element method.Computer&Mathematics with Applications,vol.57,issue 1,pp.153-168.

Pasquetti,R.;Petit,D.(1994):Inverse-heat-conduction problems with boundary elements:analysis of a corner effect.Engineering Analysis with Boundary Elements,vol.13,issue 4,pp.321-331.

Rosen,B.C.;Jin,L.(2002):Single-walled carbon nanotube–polymer composites:electrical,optical and structural investigation.Synth Metals,vol.127,issue 1-3,pp.59-62.

Schadler,L.S.;Giannaris,S.C.;Ajayan,P.M.(1998):Load transfer in carbon nanotube epoxy composites.Appl Phys Lett;vol.73,issue 26,pp.3842-3844.

Shiah,Y.C.;Tan,C.L.(1997):BEM Treatment of Two-dimensional anisotropic field problems by direct domain mapping.Engineering Analysis with BoundaryElements,vol.20,pp.347-351.

Shiah,Y.C.;Yang,R.B.;Hwang,P.W.(2004):Heat conduction in dissimilar anisotropic media with bonding defects/interface cracks,Journal of Mechanics,vol.21,no.1,pp.15-23.

Shiah,Y.C.;Shi,Y.X.(2006):Heat conduction across thermal barrier coatings of anisotropic substrates.International Communications in Heat and Mass Transfer,vol.33,pp.827-835.

Shiah,Y.C.;Tan,C.L.;Wang,C.Y.(2012):An improved numerical evaluation scheme of the fundamental solution and its derivatives for 3D anisotropic elasticity based on Fourier series.CMES-Computer Modeling in Engineering&Sciences,vol.87,issue 1,pp.1-22.

Shiah,Y.C.;Lee,Y.M.;Wang,C.C.(2013):BEM Analysis of 3D heat conduction in 3D thin anisotropic media.CMC:Computers,Materials&Continua,vol.33,issue 3,pp.231-257.

Shumakov,N.V.(1957):A method for the experimental study of the process of heating a solid body.SOVIET Physics-Technical Physics(Translated by Institute of Physics),vol.2,pp.771.

Singh,K.M.;Tanaka,M.(2001):Dual reciprocity boundary element analysis of inverse heat conduction problems.Computer Methods in Applied Mechanics and Engineering,vol.190,issues 40-41,pp.5283-5295.

Sladek,J.;Sladek,V.;Hon,Y.C.(2006):Inverse hear conduction problems by meshless local Petrov-Galerkin method.Engineering Analysis with Boundary Elements,vol.30,issue 8,pp.650-661.

Sparrow,E.M.;Haji-Sheikh,A.;Lundgren,T.S.(1964):The inverse problem in transient heat conduction.J.Appl.Mech.,vol.86,pp.369-375.

Wang,Z.;Liang,Z.;Wang,B.;Zhang,C.;Kramer,L.(2004):Processing and property investigation of single-walled carbon nanotube(SWNT)buckypaper/epoxy resin matrix nanocomposites:Composites:Part A,vol.35 pp.1225–1232.

Wei,T.;Li,Y.S.(2009):An inverse boundary problem for one-dimensional heat equation with a multilayer domain.Engineering Analysis with Boundary Elements,vol.33,issue 2,pp.225-232.

Zed,A.;Elliott,L.;Ingham,D.B.;Lesnic,D.(2000):Boundary element twodimensional solution of an inverse Stokes problem.Engineering Analysis with Boundary Elements,vol.24,issue 1,pp.75-88.