Matrix Crack Detection in Composite Plate with Spatially Random Material Properties using Fractal Dimension

K.Umesh and R.Ganguli

1 Introduction

Fiber reinforced laminated composite structures are extensively used in many engineering applications.The main advantage of composite materials over other conventional materials is the ability to be engineered according to the design requirements.Proper tailoring of composites enhance their specific stiffness,strength,fracture toughness,etc.However,composite structures are susceptible to damages.Commonly seen damages in composite structures are matrix cracks,delamination,debonding and fiber breakage/pull out[Pawar and Ganguli(2007)].Matrix cracking is often the first defect that occurs in a composite laminate subjected to a quasistatic or cyclic tensile load and low velocity impact[Takeda and Kiriyama(1999);

Adolfsson and Gudmundson(1999)].Matrix cracks cause degradation of mechanical properties of the composite structure but are not critical from a structural failure point of view.Matrix cracks trigger the next level of serious damage mechanisms such as delamination,debonding,and fiber breakage[Pawar and Ganguli(2006)].Therefore,it is important to detect matrix cracks in composite structures to prevent the development of matrix cracking-initiated damages.

In literature,there are many methods used to detect damages in composite structures.For small damages such as matrix cracks and delamination,Non-Destructive Techniques(NDT)are often used.Popular NDT’s are ultrasonic,acoustic emission,eddy current,x-ray,thermography,etc.Implementation of these conventional NDT’s is time consuming,costly,and requires a rough estimate of damage location in the case of a large structure such as an aircraft wing.Vibration based methods are well developed for damage detection of composite structures[Hu,Lee,Wu and Lu(2010);Kim and Stubbs(2003)].Damage in the structure affect the dynamic characteristics such as natural frequencies,mode shapes and damping factors.Changes in these parameters can be used for extracting damage information[Giridhara and Gopalakrishnan(2009);Zhang and Xiang(2011);Reddy and Ganguli(2007)].Vibration based methods have been considered for damage detection of structures with smart materials,which can be used to excite the structure to measure the dynamic responses.But in the case of large structures like an aircraft wing or a bridge,it is practically difficult to excite the structure to measure the frequencies and mode shapes.In such cases,a damage detection method based on static response is highly preferable compared to vibration based methods.Static deflection measurements are easier to obtain with higher levels of accuracy.

In the literature,damage detection based on static response has received less attention.Hjelmstad and Shin(1997)proposed a damage detection method based on parametric estimation scheme.Parametric estimation is done by minimizing the error between static displacements of damaged structure and undamaged structure.Bakhtiari-Nejad,Rahai and Esfandiari(2005)also used similar concept for detecting damage by minimizing the difference between the static load vector of the undamaged and damaged structure.Caddemi and Morassi(2007)considered an inverse problem based on nonlinear optimization for crack detection in beams.Yam,Li and Wong(2002)proposed damage indices based on out-of-plane static deflection and its slope and curvature.Damage detection is carried out by investigating the changes in these parameters of intact and damaged cases.Ghrib,Li and Wilbur(2012)proposed equilibrium gap concept and data-discrepancy functional based methods for damage detection in beams using static deflection.They found that these methods are able to detect concentrated and distributed damages in beams.Amiri,Hosseinzadeh,Bagheri and Koo(2013)proposed a method to detect damage in shear frames using static deflection based on diagonalization of the stiffness matrix.The concept behind these methods involves solving an inverse problem by minimizing the error between measured and predicted displacements.Here,the baseline parameter values should be known for model based prediction.This approach is computationally complex and uncertainties in baseline values will affect the accuracy of damage detection.Alternative methods are required to effectively detect damage information from the static response data without using baseline values.A damage in the structure introduces localized anomalies into the static deflection shape.Such anomalies can be amplified and extracted by using novel methods such as wavelets[Rucka and Wilde(2006);Sarangapani,Ganguli and Murthy(2013)]and fractal dimension.

Fractalsrepresenta naturalapproach fordetection ofanomaliesin Euclidean curves.The mathematical theory of fractals was first developed by Mandelbrot(1983).Inspired by the concept of Mandelbrot(1983),Katz(1988)developed a method to calculate the fractal dimension and this method is popularly used in the biological sciences.In biomedical fields,fractal dimension is used to detect transient changes in biomedical waveforms such as electroencephalograms[Esteller,Vachtsevanos,Echauz and Litt(2001);Paramanathan and Uthayakumar(2008);Raghavendra and Dutt(2009)]and medical image analysis[Lopes and Betrouni(2009)].However,in the field of damage detection,not much attention was given to the concept of fractal dimension(FD).

Selected researchers have explored the effectiveness of fractal dimension for application in structural damage detection.Hadjileontiadis,Douka and Trochidis(2005)developed a fractal dimension based crack detector to detect cracks in beams.In this study[Hadjileontiadis,Douka and Trochidis(2005)],Katz’s fractal dimension algorithm is applied to the fundamental vibration mode shape.The location of the crack is calculated by the sudden change in the value of fractal dimension and the size of crack is determined by the fractal dimension measure.Hadjileontiadis,Douka and Trochidis(2005)also found that the FD based crack detector is robust against measurement noises.Hadjileontiadis and Douka(2007)extended the FD based damage detection to two dimensional structures such as plates.Qiao,Lu,Lestari and Wang(2007)used generalized fractal dimension,a modified version of the Katz’s method,for delamination detection in composite plates.In this study[Qiao,Lu,Lestari and Wang(2007)],fractal dimension method is applied to the mode shape curvature of the damaged plate to detect the damage location.Shi,Xu,Wang and Lia(2010)applied fractal dimension method on the deflection profile of a beam with damage.Damage detection methods must not only be robust to measurement uncertainty but also to uncertainty in the structure caused by random material properties.This aspects becomes important when the damage detection algorithm is deployed across many samples of a structure[Chandrashekhar and Ganguli(2009)].Some research has addressed damage detection in composites using modal methods in the presence of uncertainty[Gayathri,Umesh and Ganguli(2010)].However,they considered uniformly distributed randomness in the composite plate.To the best of authors knowledge,the effect of spatial uncertainty in composite on fractal dimension based damage detection is not addressed in the literature.

Composite structures are manufactured through multi-stage complex processes.These processes can easily lead to variations in elastic properties and density of composite laminates[Sriramula and Chryssanthopoulos(2009)].The scatter in material properties depends on variation in micro-level properties(elastic properties of fiber and matrix)and variation in fabrication processes(fiber volume ratio,misalignment of ply orientation,fiber waviness,inter lamina voids,porosity of the matrix,incomplete curing of resin,variation in ply thickness).These will result in structural elements with uncertainties in material properties and geometry[Borkowski,Liu and Chattopadhyay(2013)].These uncertainties are generally spatially distributed in nature.

In the literature,only a few experimental studies have tried to quantify the uncertainties in composite materials.From the experiment conducted on unidirectional carbon/epoxy samples,Jeong and Shenoi(2000)found that COV ofE1,E2,G12,ν12,tensile strength and compressive strength are 4.61%,3.95%,3.14%,5.95%,14.27%and 13.5%,respectively.Variation in fibermass/unitarea and fiberstraightness influence the structural properties of the laminate and variation in resin content can lead to spatial variation in material properties and geometric distortions.Experimental studies conducted by Yurgartis(1987)show that,the variation in fiber angle in the prepreg and laminate is±3◦of the mean fiber direction and the standard deviation of the distribution varies between 0.693 to 1.936 degrees.Mehrez,Moens and Vandepitte(2012)conducted an experimental study to identify the spatial variation of composite material properties and proposed probabilistic modeling methods to model the random field from a limited number of experiments[Mehrez,Doostan,Moens and Vandepitte(2012)].Carbillet,Richard and Boubakar(2007)studied the effect of spatial variability of geometry,loading and material parameters of composite plate on failure probability.The study found that probability of failure increased by a factor of 4 when spatial variability of geometry,loading and material parameters are considered.It is clear that spatial variability can have a significant effect on the performance of composite structure.

In this paper,numerical simulation is carried out to study the effect of spatial variation of material property in damage detection of composite plate using fractal dimension.Finite element method is used to model cantilevered composite plate with damage.Here,authors have considered matrix cracks as damage since matrix cracks are the first damage mechanism often seen in composite.Matrix crack model developed by Adolfsson and Gudmundson(1997)is integrated in the finite element model.Fractal dimension based damage detection method is used to detect localized matrix cracks in a composite plate.Robustness of the damage detection method is studied by considering spatial variation in material properties of composite laminate.Spatial variation of the composite material properties is represented by two dimensional Gaussian homogeneous random field.Karhunen-Loeve(KL)expansion is used to generate a discrete random field for probabilistic analysis.This paper is a revised and expanded version of a paper presented by the authors in a conference[Umesh and Ganguli(2014)].

2 Formulation

A brief outline of the finite element model of the composite plate is provided in this section.This is followed by a discussion on the fractal dimension measure and on the modeling of spatial uncertainty.

2.1Finite element model of composite plate with matrix crack

Finite element model of composite plate is developed using classical laminated plate theory.The displacement field is

whereu,v,andware the displacement components in thex,y,andzdirections,respectively,andu0,v0,andw0are the mid-plane displacements.The rectangular non-conforming plate bending element with four nodes and five degrees of freedom per node is used for developing the finite element model for the smart composite plate.The strains associated with the displacements are

Strain displacement relation can be written in terms of nodal degrees of freedom

Stress strain relation can be written as

where¯Qis the plane stress reduced elastic tensor.Using principle of virtual displacements,equilibrium equation can be represented as

whereKis the stiffness matrix,Fis the force vector andUis the nodal degrees of freedom vector.Detailed derivation of the Eq.9 is given in[Reddy(2004)].

The matrix cracking in the composite laminate is inserted through theA,BandDstiffness matrices.The reduced stiffness matrices for the presence of matrix cracks are obtained by using Adolfsson and Gudmundson(1997)matrix crack model.

where∆A,∆Band∆Dare the residual stiffness matrices due to matrix cracks which can be defined by matrix crack densityρ

andtkandd kare the ply thickness and average distance between adjacent cracks inkthply,respectively.

2.2Fractal dimension

The fractal dimension of a curve defined by a sequence of points is estimated by[Katz(1988)]

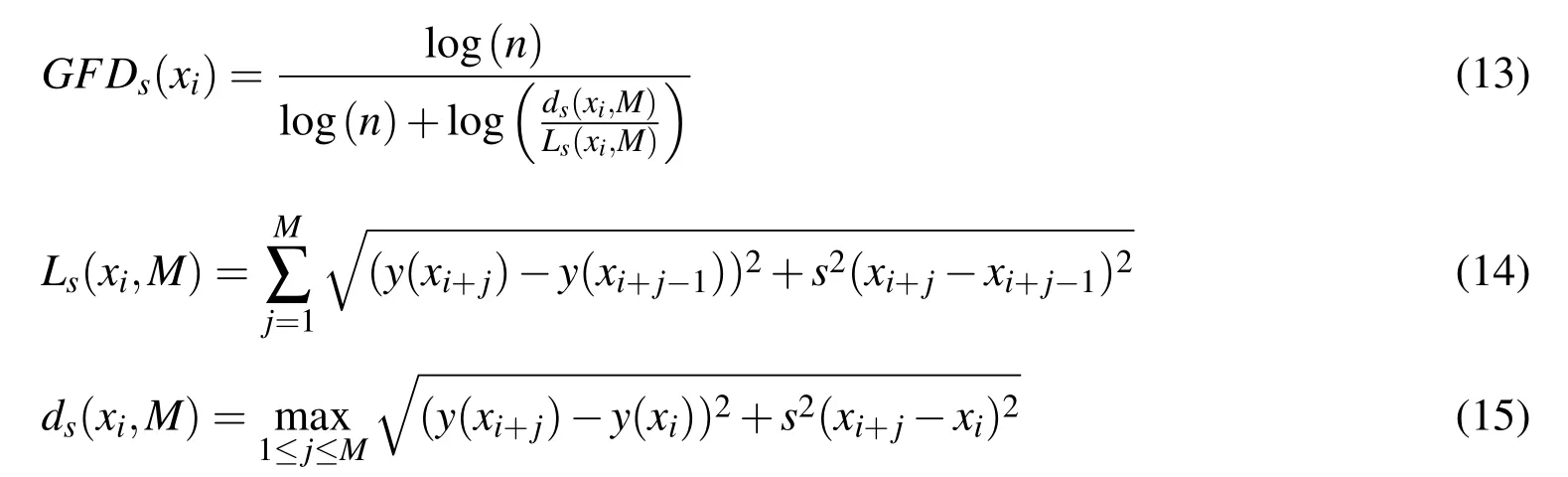
wheresis the scale parameter.

Fractal dimension scheme is constructed by employing a sliding window ofM-sample length applied to the deflection curve.The sliding window is shifted along the curve.The FD parameter is calculated using Eq.13 and the value of the estimated FD is assigned to the midpoint of sliding window.In this way,point-to-point values of the estimated FD of a curve is obtained.

For the analysis of 2D structures,such as plates,the FD operator is applied to succeeding horizontal or vertical 1D slices of the 2D deflection dataw(x,y)[Hadjileontiadis and Douka(2007)].

The estimatedF DHandF DVmatrices provide a means for scanning the plate for existence of matrix cracks.

2.3Spatial uncertainty in material property

Spatial variation of the composite material properties is represented by a two dimensional Gaussian homogeneous random field.Random variables in a random field are spatially correlated.The degree of correlation between nearby random variables can be speci fied by a covariance function.Exponential model based covariance function is widely used in uncertainty analysis of composite structures

[Murugan,Chowdhury,Adhikari and Friswell(2012);Sriramula and Chryssanthopoulos(2009)]and it can be represented as

whereC0is the variance,xijis the distance between pointsxiandx j,andlis the correlation length of the filed.Here continuous random field is discretized according to the finite element mesh,resulting inndependent random variables.A discrete random field can be represented using Karhunen-Loeve(KL)expansion[Hinke,Pichler,Pradlwarter,Mace and Waters(2011)].A discrete random fieldk(x,θ)of lengthncan be represented using KL expansion in the form

Solution of the eigenvalue problem givesneigensolutions.But onlyreigenvectors are considered in KL expansion(shown in Eq.19).The number of eigenvectors required in KL expansion depends on the value of eigenvalues.Eigenvectors corresponding to the smaller eigenvalues compared to the largest eigenvalue are neglected in the KL expansion.The criterion to find the number of modes(r)in KL expansion can be represented as[Fish and Wu(2011)]

3 Numerical results

A finite element model of the damaged composite plate structure is formulated by integrating the matrix crack model into the plate analysis as discussed in section 2.1.Fig.1 shows a laminated composite cantilever plate of dimension 200mm×200mm.The stacking sequence of the composite laminate is[θ/−θ/θ/−θ]andθ=45◦.The total thickness of the composite plate is 1 mm and each layer has the same thickness(0.25 mm).The material properties of composite materials are taken from reference[Lam,Peng,Liu and Reddy(1997)].The finite element mesh consists of 1600 rectangular plate bending elements with four nodes and five degrees of freedom per node.A uniform distributed load of 100 N/m2is applied in the negativezdirection and static analysis is conducted.Fig.2 shows the static deflection of undamaged plate under a uniform load of 100 N/m2.

3.1Localized damage detection based on fractal dimension based approach

To study the effect of localized damage on the static response of a composite plate,areaAshown in Fig.1 is considered as the region with matrix crack densityρ=4[Umesh and Ganguli(2009)].The areaAis 4%of the total plate area(200mm×200mm).Static analysis is performed for this damaged case and Fig.3 shows the center line deflection of undamaged and damaged case.Here center line deflection refers to the deflectionw(x,y=100mm)shown in Fig.1.It is clear from Fig.3 that there is almost no visible change in static deflection curve when a small localized damage is considered.So it is practically difficult to detect the presence of damage by comparing the difference in static deflection of damaged and undamaged structure.

The static deflectionw(x,y)of composite plate is processed using three different approaches:

1.Calculate fractal dimension of the deflection curve.

2.Calculate curvature of the deflection curve.

3.Calculate the fractal dimension of curvature value calculated in the second approach.

Figure 3:Center line deflection of undamaged and damaged(damage at area A)plate under a uniform load of 100 N/m2

Eq.16 is used to calculate the fractal dimension of the deflection curve andF DHis referred asF Din the following results.The curvature(∂2w/∂x2)is calculated using the central difference method.These three methods are applied to the static deflection for damaged and undamaged case.Fig.4 shows the 3 dimensional plots of above discussed three approaches for undamaged and damaged case.In this case,the damage is located at the areaAshown in Fig.1.Fig.4(a),Fig.4(c)and Fig.4(e)represent the undamaged case and Fig.4(b),Fig.4(d)and Fig.4(f)represent the damaged case.There is a clear difference in the plots given in Fig.4 due to damage at areaA.Fractal dimension of curvature shows a clearly visible change due to damage.Fig.5 shows the centerline values of the plots given in Fig.4.Fig.5(a)shows the fractal dimension of the deflection curve varies from 0.08 to 0.12 for the damaged case.This region represents the damage location for areaAshown in Fig.1.Similar trend can also be seen in Fig.5(b)and Fig.5(c)but fractal dimension of curvature shows significant change due to damage which is shown in Fig.5(c).

Next,damage is considered atdifferentlocationsotherthan atthe centerofthe plate(areaA).Here 3 cases are considered:(1)damage at areaB,(2)damage at areaCand(3)damage at both areaBandC,which are shown in Fig.1.Fig.6 shows the curvature and FD of curvature plots for three damage cases.It is clear from Fig.6(e)and Fig.6(f)that the proposed method is capable of detecting multiple damage locations from the static deflection information.Fig.7 shows the curvature values aty=60mmof Fig.6.It can be seen that the deviation of curve for damaged case from undamaged case indicates the position of the damages for the three cases.AreaBis located between 0.04 to 0.08 alongxdirection and areaCbetween 0.12 to 0.16.Fig.7(c)shows the curvature for the case 3 with multiple damages.The damaged curve(dashed line)clearly shows the multiple location of the damages.Fig.8 shows the fractal dimension of the curvature shown in Fig.7.The peaks shows the location of the damages for the three cases.These results show the ability of fractal dimension based damage detection method to amplify the effect of damage on curvature and thereby help to detect localized matrix cracks in a composite structure.

3.2Spatial uncertainty

Figure 4:Fractal dimension of deflection,curvature of deflection and Fractal dimension of curvature for undamaged(a,c,e)and damaged(b,d,f)(damage in area A in Fig.1)case

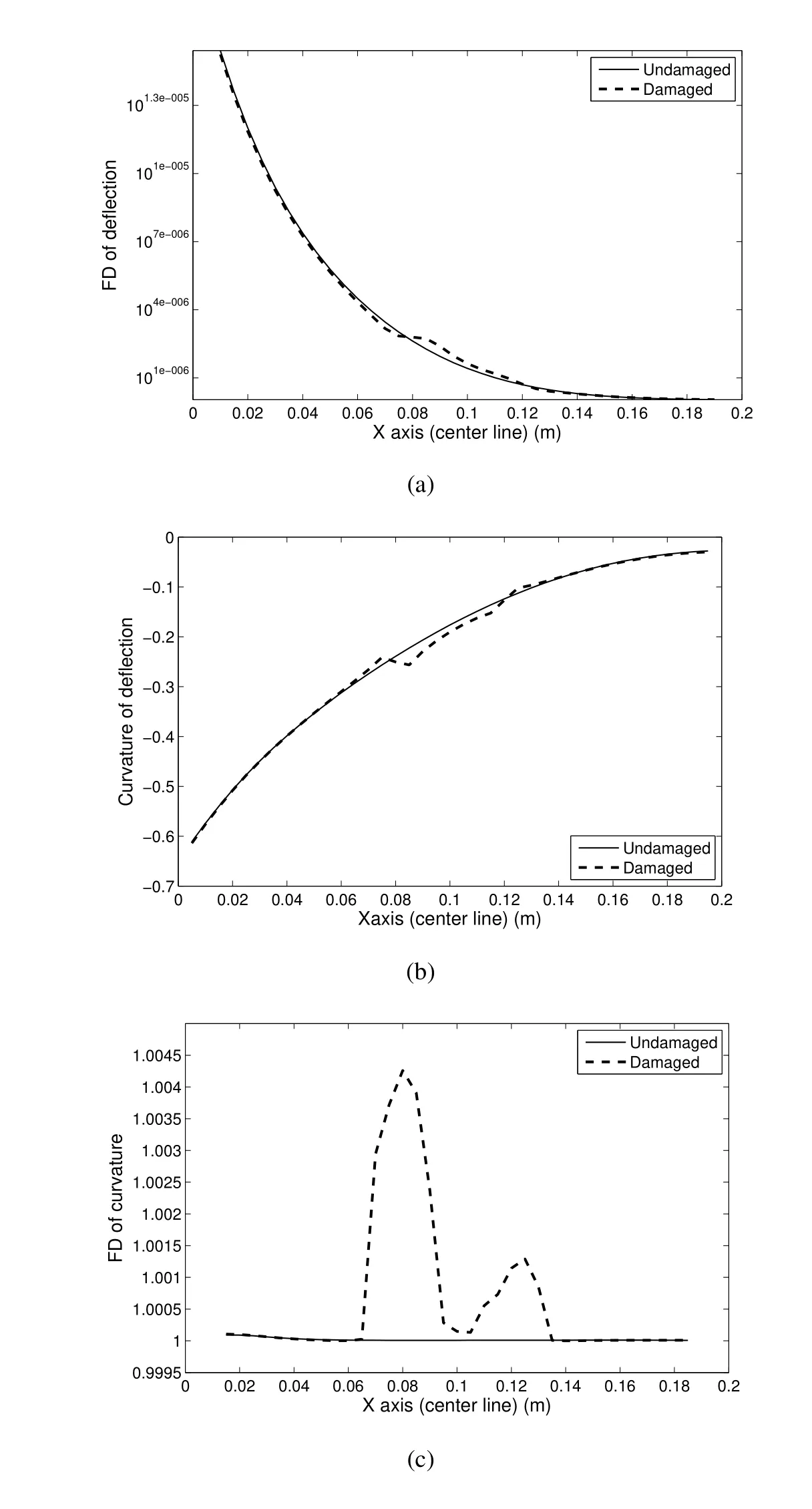
Figure 5:Center line values of Fig.4

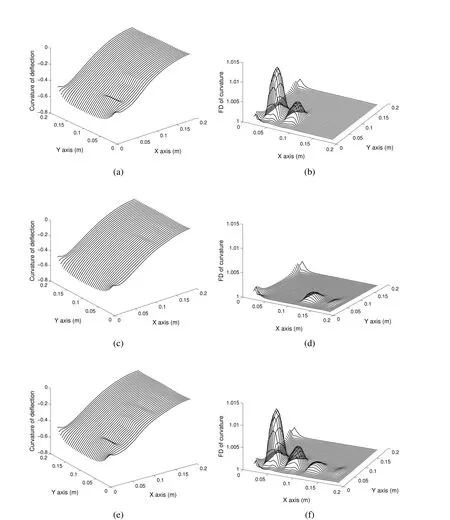
Figure 6:Curvature of deflection and FD of curvature for three different damage cases(area B(a,b),area C(c,d)and area B&C(e,f))

Figure 7:Curvature at(x,y=60mm)shown in Fig.6

Figure 8:FD of curvature at(x,y=60mm)shown in Fig.6

Figure 9:Eigen values of the covariance matrix for a correlation length of 10mm

Figure 10:Gaussian random field for a correlation length of 10mm

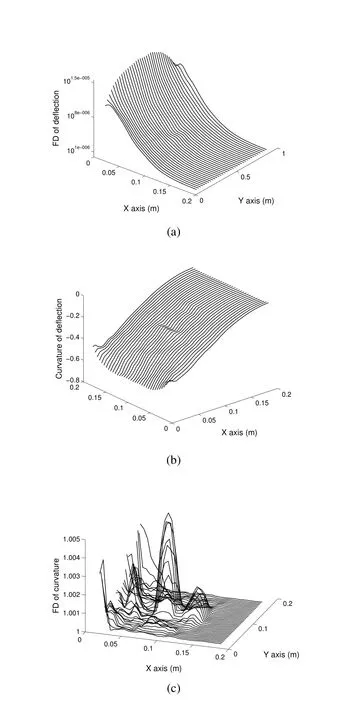
Figure 11:Fractal dimension of deflection,curvature of deflection and Fractal dimension of curvature for damaged(area A)case with spatial uncertainty

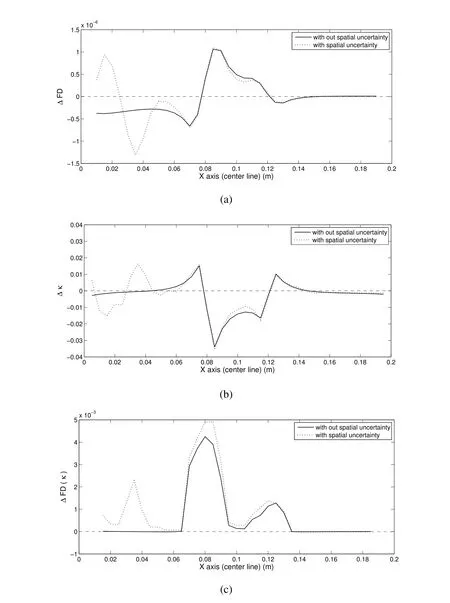
Figure 12:Delta plot of center line values of Fig.11

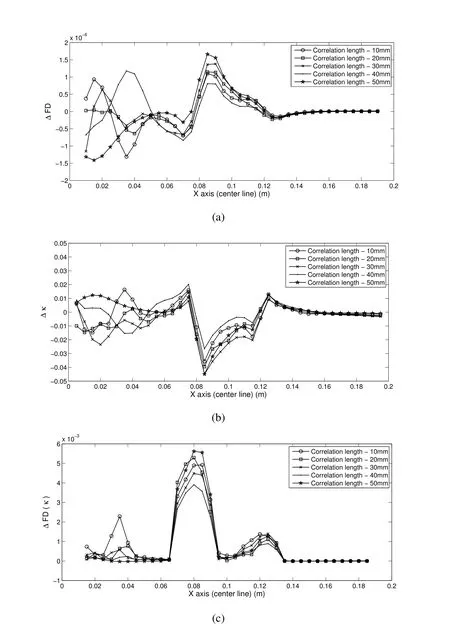
Figure 13:Delta plots for different correlation length

It is important to evaluate the performance of new damage indicator in the presence of random uncertainty.To address the spatial uncertainty in composite material properties,the lamina propertyE11is considered as a Gaussian homogeneous random field.E11has a mean value of 150Gpa and coefficient of variation of 6.97%[Umesh and Ganguli(2011)].The continuous random field is discretized according to a finite element mesh consisting of 1600 elements.The covariance matrix is calculated using Eq.18 considering the center of the element as discretization point.Here the correlation length for the graphite/epoxy laminate is assumed as 10mm[Sriramula and Chryssanthopoulos(2009);Wu,Cheng and Kang(2000)].The eigenvalues and eigenvectors of the covariance matrix of size 1600×1600 is calculated.Fig.9 shows the variation of eigenvalues of the covariance matrix.Eigenvectors with smaller eigenvalues are neglected according to the Eq.21 while formulating the KL expansion.A total of 969 terms are used in the KL expansion to represent the random field with 10mm correlation length.Latin Hypercube sampling technique is used to generate 969 Gaussian(zero mean and unit standard deviation)independent random variables.Generated independent random variables are used to form a two dimensional Gaussian random field(shown in Fig.10)using Eq.19.Random field information is fed into the finite element code to calculate static deflection with spatially varying material property.

Fractal dimension based damage detection method is applied to the static deflection of composite plate with spatially varying material property.Fig.11 shows that the proposed method is able to detect damage with spatial uncertainty.The location of the damage is clearly visible in Fig.11(b)and Fig.11(c).To compare the effect of material uncertainty on the effectiveness of the proposed method,a delta plot(damaged-undamaged)is shown in Fig.12 for a situation with and without material uncertainty.From these center line plots it is clear that the damage location is between 0.08 to 0.12 along thexaxis.There are some false peaks due to spatial uncertainty because of correlation length of 10mm which represents a sudden spatial change in material properties.Fig.13 shows the delta plots for different correlation lengths.It can be seen from Fig.13(c)that the fractal dimension based damage detection method is robust against spatial uncertainty up to a correlation length of 20mm.The main advantage of this method is that a baseline undamaged data is not required to identify the damage location.

4 Conclusions

The effectiveness of fractal dimension based damage detection method is studied considering spatial uncertainty in composite material properties.Numerical simulation of a composite cantilevered plate is carried out using finite element model.Localized matrix cracks(4%of the total plate area)are considered as damage in a composite plate.Static analysis is carried out using a finite element model and static deflection is used as input data to the damage detection algorithms.Three different methods are used for damage detection:fractal dimension of deflection,curvature of deflection and fractal dimension of curvature.It is clear from the results that while these three methods are able to determine the damage location from the static deflection information of a damaged structure,the fractal dimension of curvature looks very promising.The effectiveness of these methods in the presence of spatial uncertainty is also studied.Here,composite material properties are considered as a two dimensional Gaussian homogeneous random field.KL expansion method is used to create the random field for probabilistic analysis.It is clear from the results that the proposed methods are robust to the spatial uncertainty in composite material.Hence these methods can be used to detect small damages such as matrix cracks in a composite structure.The main advantage of these methods is the baseline undamaged information is not required for damage detection and these methodsare able to detectdamage from static deflection data which can be obtained easily relative to dynamic data such as natural frequencies and mode shapes.

Adolfsson,E.;Gudmundson,P.(1997):Thermoelastic properties in combined bending and extension of thin composite laminates with transverse matrix cracks.International Journal of Solids and Structures,vol.34,no.16,pp.2035–2060.

Adolfsson,E.;Gudmundson,P.(1999):Matrix crack initiation and progression in composite laminates subjected to bending and extension.International Journal of Solids and Structures,vol.36,no.21,pp.3131–3169.

Amiri,G.G.;Hosseinzadeh,A.Z.;Bagheri,A.;Koo,K.Y.(2013): Damage prognosis by means of modal residual force and static deflections obtained by modal flexibility based on the diagonalization method.Smart Materials and Structures,vol.22,no.7,pp.075032.

Bakhtiari-Nejad,F.;Rahai,A.;Esfandiari,A.(2005): A structural damage detection method using static noisy data.Engineering Structures,vol.27,no.12,pp.1784–1793.

Borkowski,L.B.;Liu,K.C.;Chattopadhyay,A.(2013): From ordered to disordered:The effect of microstructure on composite mechanical performance.Computers,Materials&Continua,vol.37,no.3,pp.161–193.

Caddemi,S.;Morassi,A.(2007): Crack detection in elastic beams by static measurements.International Journal of Solids and Structures,vol.44,pp.5301–5315.

Carbillet,S.;Richard,F.;Boubakar,L.(2007):Reliability indicator for layered composites with strongly non-linear behaviour.Composites Science and Technology,vol.69,no.1,pp.81–87.

Chandrashekhar,M.;Ganguli,R.(2009): Uncertainty handling in structural damage detection using fuzzy logic and probabilistic simulation.Mechanical Systems and Signal Processing,vol.23,pp.384–404.

Esteller,R.;Vachtsevanos,G.;Echauz,J.;Litt,B.(2001): A comparison of waveform fractal dimension algorithms.IEEE Transactions On Circuits And Systems I:Fundamental Theory And Applications,vol.48,no.2,pp.177–183.

Fish,J.;Wu,W.(2011): A nonintrusive stochastic multiscale solver.International Journal For Numerical Methods In Engineering,vol.88,pp.862–879.

Gayathri,P.;Umesh,K.;Ganguli,R.(2010): Effect of matrix cracking and material uncertainty on composite plates.Reliability Engineering&System Safety,vol.95,no.7,pp.716–728.

Ghrib,F.;Li,L.;Wilbur,P.(2012): Damage identification of euler–bernoulli beams using static responses.Journal of Engineering Mechanics,vol.138,no.2,pp.405–415.

Giridhara,G.;Gopalakrishnan,S.(2009): Frequency domain based damage index for structural health monitoring.Structural Durability&Health Monitoring,vol.5,no.1,pp.1–32.

Hadjileontiadis,L.J.;Douka,E.(2007):Crack detection in plates using fractal dimension.Engineering Structures,vol.29,no.7,pp.1612–1625.

Hadjileontiadis,L.J.;Douka,E.;Trochidis,A.(2005): Fractal dimension analysis forcrack identification in beam structures.MechanicalSystems and Signal Processing,vol.19,no.3,pp.659–674.

Hinke,L.;Pichler,L.;Pradlwarter,H.J.;Mace,B.R.;Waters,T.P.(2011):Modelling of spatial variations in vibration analysis with application to an automotive windshield.Finite Elements in Analysis and Design,vol.47,no.1,pp.55–62.

Hjelmstad,K.D.;Shin,S.(1997): Damage detection and assessment of structures from static response.Journal of Engineering Mechanics,vol.123,no.6,pp.568–576.

Hu,H.;Lee,C.H.;Wu,C.B.;Lu,W.J.(2010): Detection of matrix cracks in composite laminates by using the modal strain energy method.Mechanics of Composite Materials,vol.46,no.2,pp.117–132.

Jeong,H.K.;Shenoi,R.A.(2000):Probabilistic strength analysis of rectangular FRP plates using monte carlo simulation.Computers and Structures,vol.76,no.3,pp.219–235.

Katz,M.(1988):Fractals and the analysis of waveforms.Computers in Biology and Medicine,vol.18,no.3,pp.145–156.

Kim,J.T.;Stubbs,N.(2003): Crack detection in beam-type structures using frequency data.Journal of Sound and Vibration,vol.259,no.1,pp.145–160.

Lam,K.Y.;Peng,X.Q.;Liu,G.R.;Reddy,J.N.(1997): A finite-element model for piezoelectric composite laminates.Smart Materials and Structures,vol.6,pp.583–591.

Lopes,R.;Betrouni,N.(2009): Fractal and multifractal analysis:A review.Medical Image Analysis,vol.13,pp.634–649.

Mandelbrot,B.B.(1983):The Fractal Geometry of Nature.Freeman and Co.,NewYork.

Mehrez,L.;Doostan,A.;Moens,D.;Vandepitte,D.(2012):Stochastic identification of composite material properties from limited experimental databases,part II:Uncertainty modelling.Mechanical Systems and Signal Processing,vol.27,pp.484–498.

Mehrez,L.;Moens,D.;Vandepitte,D.(2012): Stochastic identification of composite material properties from limited experimental databases,part I:Experimental database construction.Mechanical Systems and Signal Processing,vol.27,pp.471–483.

Murugan,S.;Chowdhury,R.;Adhikari,S.;Friswell,M.I.(2012):Helicopter aeroelastic analysis with spatially uncertain rotor blade properties.Aerospace Science and Technology,vol.16,pp.29–39.

Paramanathan,P.;Uthayakumar,R.(2008): Application of fractal theory in analysis of human electroencephalographic signals.Computers in Biology and Medicine,vol.38,pp.372–378.

Pawar,P.M.;Ganguli,R.(2006):Modeling progressive damage accumulation in thin walled composite beams for rotor blade applications.Composites Science and Technology,vol.66,no.13,pp.2337–2349.

Pawar,P.M.;Ganguli,R.(2007): On the effect of progressive damage on composite helicopter rotor system behavior.Composite Structures,vol.78,no.3,pp.410–423.

Qiao,P.Z.;Lu,K.;Lestari,W.;Wang,J.(2007):Curvature mode shape-based damage detection in composite laminated plates.Composite Structures,vol.80,pp.409–428.

Raghavendra,B.S.;Dutt,D.N.(2009):A note on fractal dimensions of biomedical waveforms.Computers in Biology and Medicine,vol.39,pp.1006–1012.

Reddy,J.N.(2004):Mechanics of Laminated Composite Plates and Shells:Theory and Analysis,Second Edition.CRC Press.

Reddy,K.V.;Ganguli,R.(2007):Fourier analysis of mode shapes of damaged beams.Computers,Materials,&Continua,vol.5,no.2,pp.79–98.

Rucka,M.;Wilde,K.(2006):Crack identification using wavelets on experimental static deflection profiles.Engineering Structures,vol.28,no.2,pp.279–288.

Sarangapani,G.;Ganguli,R.;Murthy,C.R.L.(2013): Spatial wavelet approach to local matrix crack detection in composite beams with ply level material uncertainty.Applied Composite Materials,vol.20,no.4,pp.719–746.

Shi,J.;Xu,X.;Wang,J.;Lia,G.(2010):Beam damage detection using computer vision technology.Nondestructive Testing and Evaluation,vol.25,no.3,pp.189–204.

Sriramula,S.;Chryssanthopoulos,M.K.(2009):Quantification of uncertainty modelling in stochastic analysis of FRP composites.Composites:Part A,vol.40,no.11,pp.1673–1684.

Takeda,N.;Kiriyama,M.(1999): Matrix crack evolution in SiC fiber/glass matrix cross-ply laminates.Composites:Part A,vol.30,pp.593–597.

Umesh,K.;Ganguli,R.(2009):Shape and vibration control of smart composite plate with matrix cracks.Smart Materials and Structures,vol.18,pp.025002.

Umesh,K.;Ganguli,R.(2011):Composite material and piezoelectric coefficient uncertainty effects on structural health monitoring using feedback control gains as damage indicators.Structural Health Monitoring,vol.10,no.2,pp.115–129.

Umesh,K.;Ganguli,R.(2014): Matrix crack detection in spatially random composite structures using fractal dimension.InProc.SPIE 9063,Nondestructive Characterization for Composite Materials,Aerospace Engineering,Civil Infrastructure,and Homeland Security,volume 90630V.

Wu,W.F.;Cheng,H.C.;Kang,C.K.(2000): Random field formulation of composite laminates.Composite Structures,vol.49,no.1,pp.87–93.

Yam,L.H.;Li,Y.Y.;Wong,W.O.(2002): Sensitivity studies of parameters for damage detection of plate-like structures using static and dynamic approaches.Engineering Structures,vol.24,no.11,pp.1465–1475.

Yurgartis,S.W.(1987): Measurement of small angle fiber misalignments in continuous fiber composites.Composites Science and Technology,vol.30,no.4,pp.279–293.

Zhang,Y.;Xiang,Z.H.(2011):Frequency shift curve based damage detection method for beam structures.Computers,Materials&Continua,vol.26,no.1,pp.19–36.