基于分段MDCFT 的LFM 信号参数估计方法

袁德生,韩 松

（中国科学院电子学研究所,北京,100190）

1 MDCFT 算法形式与性质

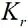
2 MDCFT 的分段序列变换特性

对于一个LFM 信号，其调频率是固定的，而中心频率取决于序列的有效相位部分的起止时刻。按照MDCFT 的定义，序列起点时刻为，终点时刻为，那么中心频率为时的频率。然而，通常已知LFM 脉冲的宽度，但是未知脉冲的起止时刻。

图1 部分序列变换原理

对该信号做MDCFT 变换

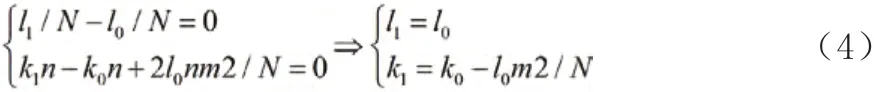
3 分段序列MDCFT 变换的参数检测估计方法

在上一节的分析中看到，当LFM 脉冲信号的起止时刻未知时，信号的中心频率将无法正确估计。本节旨在提供一种恢复中心频率的方法。考虑4 式和5 式，以及两个段中的聚焦幅度，可以得到以下关系：信号在，两段中的中心频率偏移量之比与检测幅度之比成反比；信号在两段中的中心频率之差为调频率的两倍。这两组关系构成了同一信号在分段变换时两个段之间的纽带，是恢复原始信号参数的基础。假设一长度为N 的离散LFM 序列具有参数。该序列随机分布在数个依序的变换段中的两个邻近分段中。在分段的MDCFT 变换中，在变换段中通过峰值检测得到参数为,聚焦幅度为的LFM 信号。该信号可能属于一下三种信号在断的变换结果：

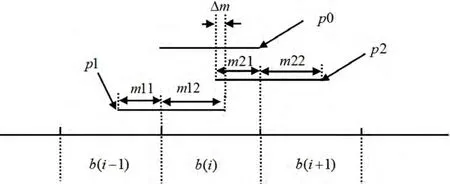
图2 分段MDCFT 原理

上述情况（1）只是后两种的特殊形式，这里仅讨论后两种形式。

对以上结论的证明：

根据聚焦幅度关系可求得长度

对其,做MDCFT 变换有

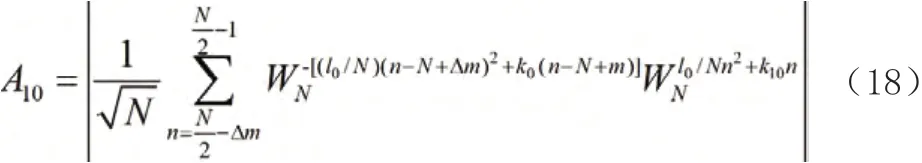
结合幅度长度关系可得交错项长度

带入式18 并结合相关式整理得：

4 仿真与结论

表1 在不同起始空白的条件下的参数估计结果

?

从上表分析中得出，调频率和中心频率的估计都接近真实值，是比较准确的参数估计。相比之下，调频率的估计平均误差更小，而中心频率的估计平均误差更大。这是因为在分段估计时，信号的幅度受到旁瓣电平的叠加造成幅度比例略微的改变。仿真，相比于常规的MDCFT，本方法的对调频率的估计没有改善。但是在变换段内有无效空白时，本方法可以对于中心频率实现正确的估计，具有工程实用性。

[1] Raney,R K.Synthetic aperture imaging radar and moving targets[J].IEEE Transactions on Aerospace and Electronic Systems,1971,AES-7(3):499-505

[2] Edgar F Velez,Richard G Absher.Spectral estimation based on the Wigner-Ville representation[J]. Signal Processing, 1990, 20(4):325-346

[3] L B Almeida.The Fractional Fourier Transform and Time-frequency Representation[J].IEEE Transactions on Signal Processing,1994,42(11):3084-3091

[4] 孙泓波,郭欣,顾红,苏卫民,等.修正离散Chirp-Fourier 变换及其在SAR 运动目标检测中的应用[J].电子学报,2003, 31(1):25-28