LDA-CF:一种混合协同过滤方法
2014-04-14廉涛王帅强崔超然
廉涛,马 军,王帅强,崔超然
(1.山东大学,山东济南250101;2.山东财经大学,山东济南250014)
1 引言
在这个信息爆炸的时代,信息过载已成为人们日常生活中面临的主要问题之一,于是近年来个性化推荐系统得到了学术界和产业界的广泛关注。目前大多数推荐系统都利用协同过滤(Collaborative Filtering),从历史数据(如以前用户对物品的评分)中发现用户和物品的联系,预测用户对未知物品的评分,从而进行个性化推荐[1]。
协同过滤主要分为两大类:
(1)邻域方法(Neighborhood Method)。首先使用评分矩阵计算用户或者物品相似度,寻找目标用户的邻居用户或者未知物品的邻居物品;然后根据邻居用户或者邻居物品的评分,预测目标用户对未知物品的评分[2-3]。
(2)潜在因素模型(Latent Factor Model)。首先从评分矩阵中发现用户和物品潜在因素向量,用户潜在因素向量表示用户的兴趣,物品潜在因素向量表示物品的特点;然后根据目标用户和未知物品对应的潜在因素向量预测未知评分。该类方法常用的技术是矩阵分解[4-5]。
实际应用中,由于大多数用户只对少数物品评分,所以即便两名用户兴趣相似,他们共同评分的物品也可能很少。数据的稀疏性对以上两类方法提出了严峻挑战[6]。混合模型能够有效地缓解数据稀疏问题[7]。LDA主题模型是一种概率混合模型[8],通过对词汇间接地进行模糊聚类,发现大型语料库中的潜在主题,把文档从高维词汇空间映射到低维主题空间,进而可以在低维主题空间中计算文档相似度。如果我们换个视角看待评分矩阵,将物品看作词汇,用户对物品的评分看作词频,用户所有的评分就可以转换成一篇伪文档。假如物品集合共有5种物品{i1,i2,i3,i4,i5},某名用户对物品的评分向量为(0,4,1,0,3),则对应的伪文档的内容就是“i2i2i2i2i3i5i5i5”。这样我们就可以使用LDA对物品间接地进行模糊聚类,从评分矩阵中发现潜在主题,通过潜在主题把用户和物品联系起来,将用户和物品表示为潜在因素向量,进而在低维潜在因素空间计算用户和物品相似度。
本文提出一种混合协同过滤方法LDA-CF,该方法结合了潜在因素模型和邻域方法。我们首先将评分矩阵转换为伪文档集合,使用LDA发现潜在主题,将用户和物品表示成潜在因素向量;然后在低维潜在因素空间,计算用户和物品相似度;最后寻找目标用户的邻居用户或者未知物品的邻居物品,根据邻居用户或者邻居物品的评分预测未知评分。在MovieLens 100k数据集上的实验表明:在评分预测任务中,LDA-CF取得的MAE性能指标优于传统的邻域方法。因此,LDA可以有效地从评分矩阵中发现对计算相似度十分有用的用户和物品低维特征表示,在一定程度上缓解了数据稀疏问题。
本文第2节介绍协同过滤和混合模型在推荐系统中的相关工作;第3节讲述本文方法LDA-CF的细节;第4节展示实验结果与分析;第5节总结与展望。
2 相关工作
2.1 协同过滤
协同过滤是一种广泛使用的推荐方法,主要有两类:邻域方法和潜在因素模型。
邻域方法主要包括基于物品的协同过滤(Item-Based CF)和基于用户的协同过滤(User-Based CF)。基于物品的协同过滤[2]主要分以下三步:首先根据评分矩阵计算物品之间的相似度;然后在目标用户已经评分的物品中选择和未知物品最相似的K种物品作为邻居物品;最后根据目标用户对邻居物品的评分预测他对未知物品的评分。基于用户的协同过滤[3]基本类似,主要是寻找和目标用户兴趣相似的邻居用户。该类方法最大的问题是,在高维空间中基于稀疏数据计算的相似度并不准确。
潜在因素模型一般通过最小化均方误差损失函数,寻找原始评分矩阵的一个最佳近似低秩矩阵R^=UTV,其中U和V的列向量分别对应用户和物品潜在因素向量,二者的内积表示预测评分。由于评分矩阵的稀疏性,早期的工作[9]先填充缺失值,再使用奇异值分解得到用户和物品潜在因素向量。这样不仅会增加计算量,而且会引入噪声。近年来的工作在目标函数中加入正则化项,只使用已知评分进行概率矩阵分解[5]。此外,Koren把潜在因素模型和邻域方法集成到一个目标函数中[10],将二者结合起来。
2.2 混合模型
Hofmann提出的隐语义模型(Latent factor Model)通过隐类(Latent Class)将用户和物品联系起来[11]。认为用户并不是直接对物品产生兴趣,而是物品属于不同的类别,用户对几个类别有兴趣。这个模型可以从用户行为数据中学习出这些类别,以及用户对类别的兴趣。他也曾将pLSA(probabilistic Latent Semantic Analysis)扩展到协同过滤推荐系统中[12]。
Marlin则提出了URP(User Rating Profile)模型[13],将LDA中的词汇变量替换为评分变量,对用户的评分行为进行建模。URP试图发现评分矩阵中潜在的用户态度(User Attitude),每种用户态度对应一种评分模式,即评分{1,2,3,4,5}的多项式分布,而非词汇的多项式分布。每名用户拥有一种态度多项式分布。然后根据用户-态度多项式分布和态度-评分多项式分布,预测用户对物品的评分。
LDA主题模型是一种概率混合模型,通过潜在主题将文档和词汇联系起来。假设文档集合中有Z个潜在主题,每个主题被表示为一种词汇多项式分布φz,每篇文档被看作多个主题的混合,对应一种主题多项式分布θd。一方面LDA分别实现了文档和词汇的模糊聚类,每个词汇可能属于多个主题,每篇文档也可能包含多个主题。另一方面LDA可以被看作一种类似于pLSA的降维方法[14],将文档从高维词汇空间映射到低维主题空间。此外Jin系统地研究了混合模型(Mixture Model)在协同过滤中的应用[7]。所以本文试图将LDA应用到协同过滤中,进行个性化推荐。
3 本文方法LDA-CF
假设用户集合U有m名用户,物品集合I有n种物品,评分矩阵R={ru,i}m×n,其中ru,i∈{1,2,3,4,5}表示用户u对物品i的评分(评分范围依具体应用而定)。如果用户u未对物品i评分,则用0表示。协同过滤的主要任务就是预测用户对未知物品的评分。
本文提出一种结合潜在因素模型和邻域方法的混合协同过滤方法LDA-CF,来完成推荐系统中的评分预测任务。一方面类似于潜在因素模型,本文使用LDA从评分矩阵中发现潜在主题,通过潜在主题将用户和物品联系起来,用潜在因素向量描述用户的兴趣和物品的特点;另一方面类似于邻域方法,本文在低维潜在因素空间,计算用户和物品相似度,根据邻居用户或邻居物品的评分预测未知评分。此外,混合模型可以有效地缓解数据稀疏问题[7]。在这种混合模型中,物品可能不同程度地属于多个主题,用户也可能不同程度地对多个主题感兴趣。即便两名用户共同评分的物品很少,或者同时对两种物品评分的用户很少,也可以基于潜在因素向量计算用户和物品相似度。
LDA-CF主要分以下几步:
1)发现潜在因素向量:将评分矩阵转换成伪文档集合,使用LDA发现潜在主题,将用户和物品表示成潜在因素向量;
2)计算相似度:在低维潜在因素空间,基于KL散度(Kullback-Leibler Divergence)或JS散度(Jensen-Shannon Divergence),计算用户或者物品之间的相似度;
3)预测评分:寻找目标用户的邻居用户或者未知物品的邻居物品,根据邻居用户或邻居物品的评分预测目标用户对未知物品的评分。
3.1 发现潜在因素向量
如果从LDA主题模型的视角看待评分矩阵R,每种物品i对应一个单词w,每名用户u对应一篇由物品组成的伪文档du,用户u对物品i的评分ru,i等于物品i在伪文档du中出现的次数,那么就可以将评分矩阵转换成伪文档集合。假设物品集合I共有5种物品{i1,i2,i3,i4,i5},用户u对物品集合的评分向量为(0,4,1,0,3),则伪文档du的内容就是“i2i2i2i2i3i5i5i5”。这样我们就可以只使用已知评分,忽略评分矩阵中大量的缺失值。
然后我们使用LDA发现伪文档集合中的潜在主题,通过潜在主题将用户和物品联系起来。每个主题z对应物品集合I上的一种多项式分布φz,每名用户u拥有一种潜在主题上的多项式分布θu。用户对物品的评分行为可以这样描述:用户u首先根据自己的兴趣θu选择一个主题z,然后根据该主题所对应的物品多项式分布φz选择一种物品,不断重复此过程,用户u选择物品i的次数越多,对它的评分ru,i就越大。图模型表示如图1,对应的生成过程如下:
1)对于用户集合U中的每名用户u,采样θu~Dirichlet(α);
2)对于用户u对应的伪文档du中每个位置的物品iu,n:
a)采样一个主题标签zu,n~Multinomial(θu);
b)采样一种物品iu,n~Multinomial(φzu,n)。

图1 LDA图模型表示
如果在伪文档集合上训练一个包含Z个主题的LDA模型,那么用户u对应的潜在因素向量就可以用伪文档du在Z个主题上的多项式分布θu=来表示,其中≤1。物品i对应的潜在因素向量也可以由它在Z个主题中出现的概率组成的向量ηi=(φ1,i,φ2,i,…,φZ,i)来表示。虽然每个主题z对应的物品多项式分布φz中,各种物品出现的概率之和为1。但是每种物品在各个主题中出现的概率之和并不为它出现在各个主题中的概率互不影响,可以都很高或很低。因此我们对物品i对应的潜在因素向量ηi进行线性规范化,ηi,z=
此模型可以为同一种物品在一篇伪文档中的多次出现选择不同的主题标签。因此一种物品可以属于多个主题,每名用户也可能对多个主题感兴趣。
3.2 计算相似度
协同过滤中普遍使用余弦相似度或皮尔逊相关系数(Pearson Correlation Coefficient)度量用户和物品相似度。由于两名用户共同评分的物品很少,同时对两种物品评分的用户也很少,在高维空间中基于存在共同评分的少数几个维度计算相似度并不准确。即便两名用户各自评分的物品并不少,如果他们共同评分的物品很少,他们之间的相似度也接近于0。计算物品相似度也存在类似问题,即维度灾难(Curse of Dimensionality)。
在低维潜在因素空间中计算相似度可以有效地缓解数据稀疏问题。如果两名用户各自评分的物品并不少,他们对应的潜在因素向量就能够准确地描述各自的兴趣。即便没有共同评分的物品,如果各自评分的某些物品属于相同的主题,那么他们的兴趣也会相似,根据潜在因素向量计算的相似度也会比较高。如果某名用户评分的物品特别少,那么他所对应的潜在因素向量在各个主题上的分布就比较均匀,但也可以计算和其他用户的相似度,这样在一定程度上解决了“冷启动”问题。同样的道理也适用于物品相似度的计算。
KL散度和JS散度用来度量两个概率分布之间的距离,我们利用下式计算用户和物品相似度,其中P和Q表示两个概率分布。将用户潜在因素向量θu和θv代入,就可以计算两名用户的相似度,将物品潜在因素向量ηi和ηj代入,就可以计算两种物品的相似度。
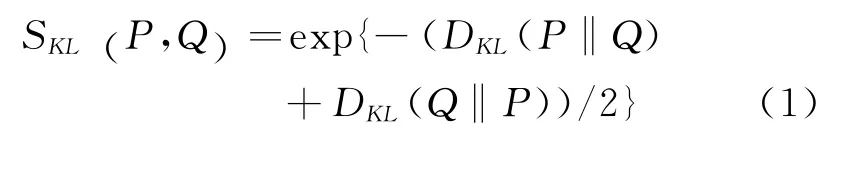
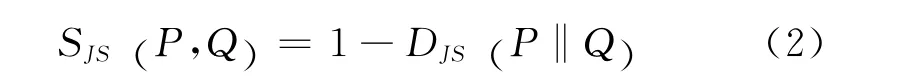
3.3 预测评分
在低维潜在因素空间计算完用户和物品相似度之后,我们采用邻域方法预测未知评分:寻找目标用户的邻居用户或者未知物品的邻居物品,根据邻居用户或者邻居物品的评分,预测目标用户对未知物品的评分。
在邻域方法中,评分预测公式主要有两种:加权平均评分(Weighted Average Rating)和加权平均偏差(Weighted Average Deviation)。加权平均偏差考虑了用户或物品的个体差异。
以基于物品的协同过滤为例,加权平均评分如下式:
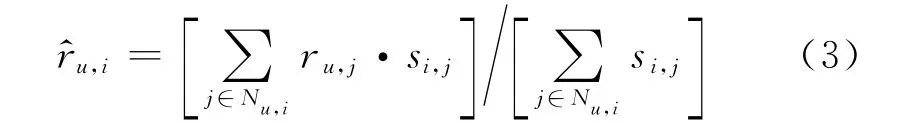
以基于用户的协同过滤为例,加权平均偏差如下式:
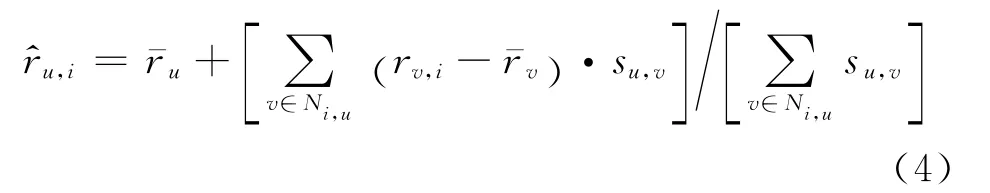
4 实验结果与分析
实验使用MovieLens 100k电影评分数据,包括来自943名用户对1 682部电影的100 000个评分,评分范围为{1,2,3,4,5}。数据稀疏度为1-100 000/(943*1 682)=0.937 0。数据集也非常不平衡,某名用户已评分的物品数目变化范围为[20,737],对某种物品已评分的用户数目变化范围为[1, 583]。我们采用5折交叉验证,每次使用20 000个评分作为测试集,剩余80 000个评分作为训练集,取5次实验的平均结果。
我们选择邻域方法作为基准方法,基于原始评分矩阵,根据余弦相似度和皮尔逊相关系数计算用户和物品相似度,分别简写为Rating-CF-Cos和Rating-CF-Pcc。本文方法LDA-CF则基于用户和物品潜在因素向量,根据KL散度和JS散度计算用户和物品相似度,分别简写为LDA-CF-KL和LDA-CF-JS。
我们采用平均绝对误差(MAE)和覆盖度(Coverage)作为评价指标。MAE度量测试集中用户u对物品i的预测评分和实际评分ru,i的误差,MAE值越小,说明预测越准确。覆盖度度量邻居数目K对基于邻居预测能力的影响,覆盖度越高,说明能对测试集中更多的用户-物品对(u,i)预测评分。

其中Test表示测试集中的全部用户-物品对(u,i),N<K表示测试集中邻居用户或者邻居物品数目不足K的用户-物品对(u,i)的数目。
4.1 主题数目的影响
首先我们设定邻居数目K=20,LDA模型参数α=0.5,β=0.1,观察随着主题数目Z的变化,LDACF基于邻居用户和基于邻居物品采用加权平均偏差预测评分时,MAE的变化情况。从图2中可以看出,主题数目从10变化到50时,LDA-CF的效果并无太大差异,MAE变化范围小于0.005,说明LDA-CF对主题数目并不敏感。这可能是因为相对于传统文本文档中词频的变化范围而言,伪文档中物品出现的次数差异并不大。
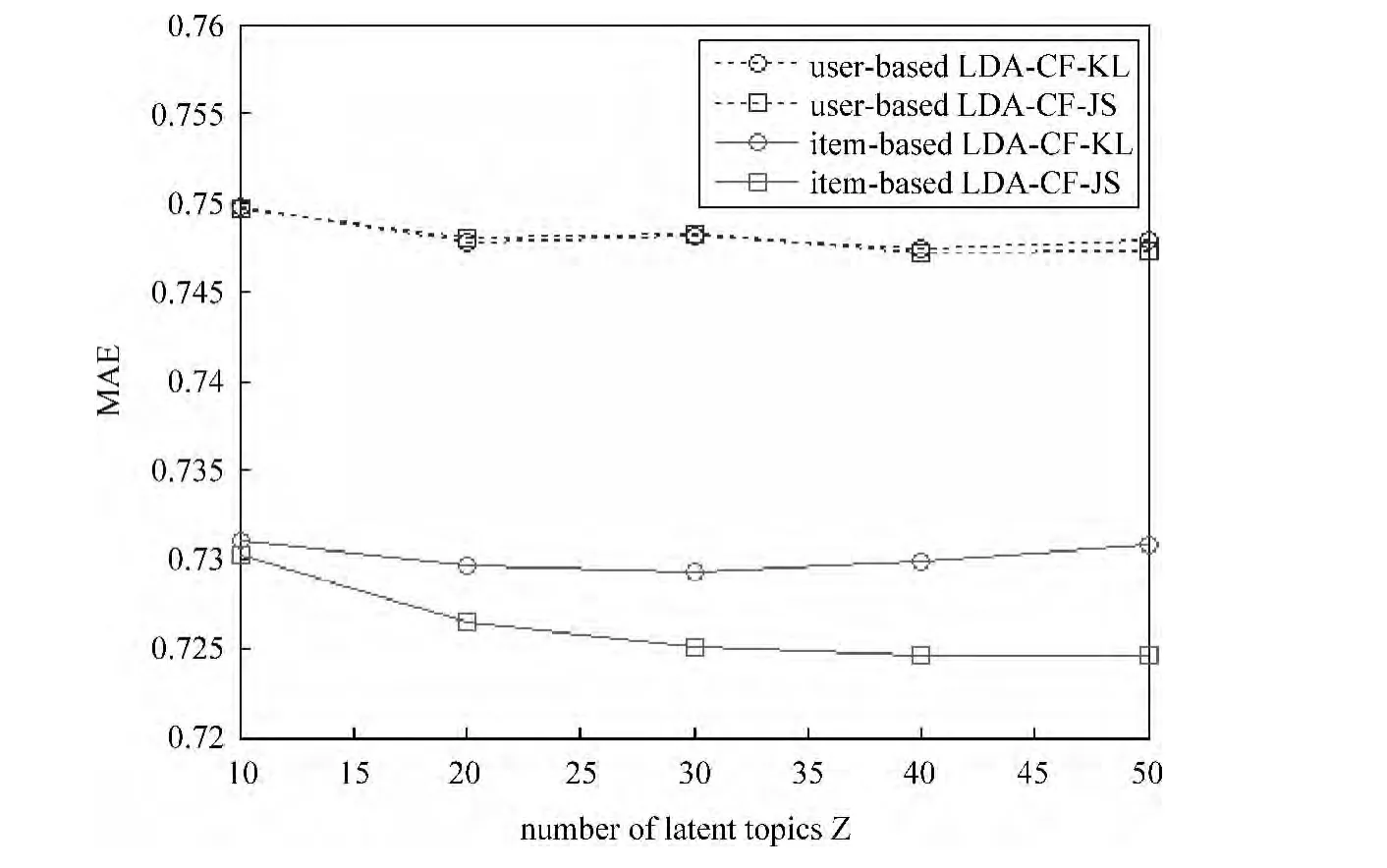
图2 LDA主题数目对MAE的影响
4.2 邻居数目的影响
然后我们设定LDA主题数目Z=20,观察邻居数目K对覆盖度和MAE的影响。
由于我们不是先设定相似度阈值再选择邻居,而是把相似度从大到小排序选择前K个作为邻居,所以相似度的计算方式和具体数值对邻居数目没有影响。覆盖度仅受邻居数目的影响。从图3中可以看出,基于邻居用户和基于邻居物品时,覆盖度都随邻居数目的增大而显著下降,并且基于邻居物品的覆盖度略高于基于邻居用户的覆盖度。
图4和图5展示了Rating-CF-Pcc和LDA-CFJS分别使用加权平均评分和加权平均偏差预测评分时,基于邻居用户和邻居物品的MAE值随邻居数目K的变化情况。图4中各种方法的变化趋势略有不同,而图5中各种方法的变化趋势基本一致。当K=20时,MAE值最小;当K<20时,由于邻居太少,预测效果比较差;当K>20时,随着邻居数目的增多,引入了越来越多相似度较低的用户或者物品,预测效果也越来越差。不过图4和图5都表明:无论基于邻居用户或邻居物品,LDA-CF-JS始终比Rating-CF-Pcc效果要好。

图3 邻居数目对覆盖度的影响

图4 加权平均评分时,邻居数目对MAE的影响

图5 加权平均偏差时,邻居数目对MAE的影响
4.3 本文方法与基准方法
最后我们设置主题数目Z=20,邻居数目K=20,在基于邻居用户和基于邻居物品时,分别采用加权平均评分和加权平均偏差预测评分,总共4种实验配置下,对比本文方法LDA-CF和基准方法Rating-CF取得的MAE值。
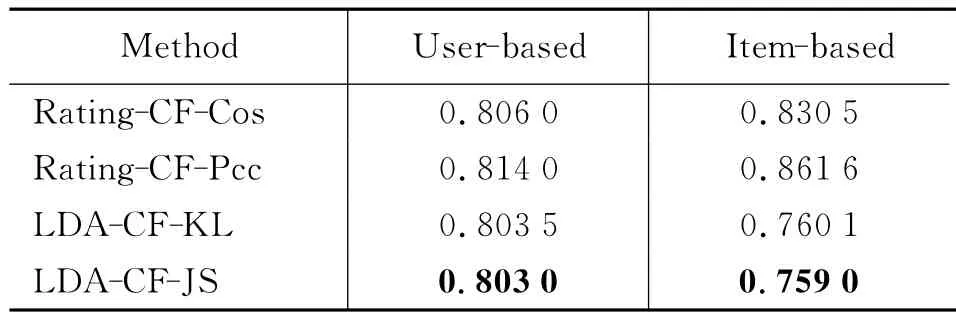
表1 加权平均评分MAE值
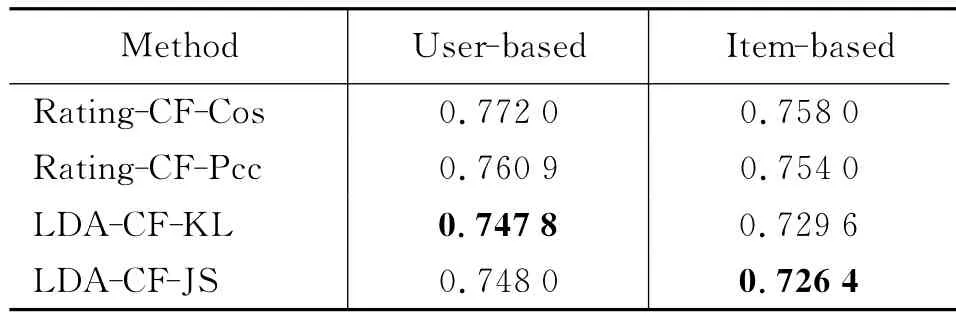
表2 加权平均偏差MAE值
从表1和表2中我们可以得出以下结论:
(1)在评分预测任务中,除了Rating-CF使用加权平均评分之外,基于邻居物品比基于邻居用户预测更准确。说明推荐目标用户喜欢的物品的相似物品,比推荐目标用户的相似用户喜欢的物品,效果要好;
(2)无论基于邻居用户或邻居物品,加权平均偏差的结果明显好于加权平均评分的结果。说明考虑用户评分行为的差异和物品受欢迎程度的差异会提高推荐效果;
(3)无论基于邻居用户或邻居物品,无论采用加权平均评分或加权平均偏差预测评分,本文方法LDA-CF比基准方法Rating-CF取得的MAE值都小。说明了虽然同样是基于邻居预测评分,使用LDA发现的潜在因素向量计算相似度比使用原始评分矩阵计算相似度更准确,推荐效果更好。
5 总结与展望
本文提出了一种结合潜在因素模型和邻域方法的混合协同过滤方法LDA-CF。我们从LDA主题模型的视角看待评分矩阵,将物品看作词汇,用户看作文档,用户对物品的评分看作词频,从而将评分矩阵转换成伪文档集合。首先利用LDA发现伪文档集合中的潜在主题,通过潜在主题将用户和物品联系起来,用潜在因素向量描述用户的兴趣和物品的特点;然后使用潜在因素向量计算用户和物品相似度;最后采用邻域方法预测未知评分。在评分预测任务中,LDA-CF比直接使用原始评分矩阵的基于邻居的协同过滤方法,预测更加准确。说明了LDA可以有效地从评分矩阵中发现对计算相似度十分有用的用户和物品低维特征表示,在一定程度上缓解了数据稀疏问题。
基于本文的初步结果,未来我们想进一步检验本文方法在更大规模的数据集上的效果和效率,研究LDA等概率混合模型能否提高推荐结果的多样性,探索考虑时间因素的动态推荐系统中的关键技术。
[1] Goldberg D,Nichols D,Oki B M,et al.Using collaborative filtering to weave an information tapestry[J].Commun.ACM,1992,35(12):61-70.
[2] Sarwar B,Karypis G,Konstan J,et al.Item-based collaborative filtering recommendation algorithms[C]//Proceedings of the 10th international conference on World Wide Web,2001,285-295.
[3] Herlocker J L,Konstan J A,Borchers A l,et al.An algorithmic framework for performing collaborative filtering[C]//Proceedings of the 22nd ACM SIGIR,1999,230-237.
[4] Koren Y,Bell R,Volinsky C.Matrix factorization techniques for recommender systems[J].Computer,2009,42(8):30-37.
[5] Salakhutdinov R,Mnih A.Probabilistic matrix factorization[C]//Proceedings of the 20th NIPS,2007.
[6] 周涛.个性化推荐的十大挑战[J].中国计算机学会通讯,2012,8(7):48-61.
[7] Jin R,Si L,Zhai C X.A study of mixture models for collaborative filtering[J].Inf.Retr.,2006,9(3):357-382.
[8] Blei D M,Ng A Y,and Jordan M I.Latent dirichlet allocation[J].J.Mach.Learn.Res.,2003,3:993-1022.
[9] Sarwar B M,Karypis G,Konstan J A,et al.Application of dimensionality reduction in recommender system—a case study[C]//Proceedings of WebKDD at the 6th ACM SIGKDD,2000.
[10] Koren Y.Factorization meets the neighborhood:a multifaceted collaborative filtering model[C]//Proceedings of the 14th ACM SIGKDD,2008,426-434.
[11] Hofmann T,Puzicha J.Latent class models for collaborative filtering[C]//Proceedings of the 16th IJCAI,1999,688-693.
[12] Hofmann T.Latent semantic models for collaborative filtering[J].TOIS,2004,22(1):89-115.
[13] Marlin B.Modeling user rating profiles for collabora-tive filtering[C]//Proceedings of the 17th NIPS,2003.
[14] Steyvers M,Griffiths T.Probabilistic topic models[M].In Landauer T,McNamara D S,Dennis S,et al.(Eds.),Handbook of Latent Semantic Analysis.Hillsdale,NJ:Erlbaum.2007.
