抛物型方程的一个新的数值格式

王自强(贵州民族大学 理学院，贵州 贵阳 550025)

0 引言

在渗流、热传导、扩散等领域中常常会遇到求解抛物型方程的问题，对这一类方程的数值求解一直是科学工作者研究的热点问题之一，如文献[1-5]。本文考虑如下一维抛物型方程：

满足下列初值条件：

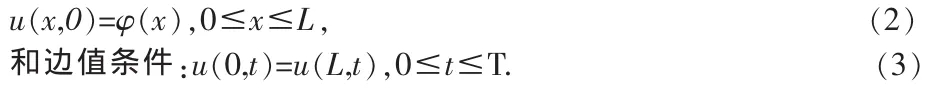
求解上述抛物型问题，方法很多，典型的方法有：有限差分法，有限元法，谱方法，谱元法，无网格法，有限体积法等。本文利用半步长格式和交替方向法构造了一个数值格式，理论分析证明该格式是绝对稳定的。

1 差分格式的构造

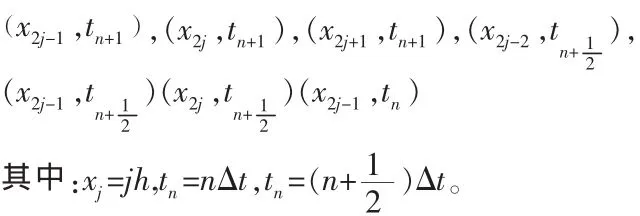
在上述七个节点上u的值在节点（jh，nΔt）处做Taylor展开，便得到式（1）的差分格式，格式分两块，如下：

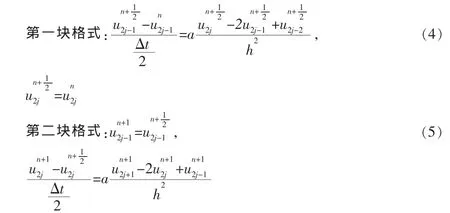
其中j=1,2，…，M，容易验证，格式(4)和格式(5)的截断误差均为：O（τ+h2）。 令为网比，由此得到(4)和(5)的差分方程组的矩阵形式如下∶

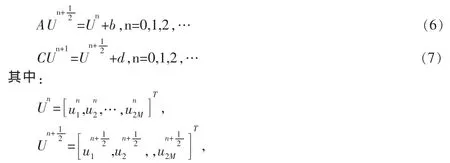
系数矩阵A，C和右端向量吧b，d如下：

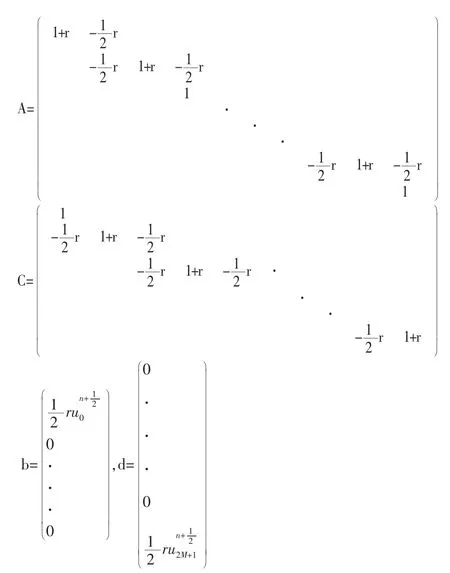
2 稳定性分析

引理 1(胡家赣引理)设M=（mij）为 n×n 矩阵，N=（nij）为 n×m 矩阵，且M为严格对角占优矩阵，则：

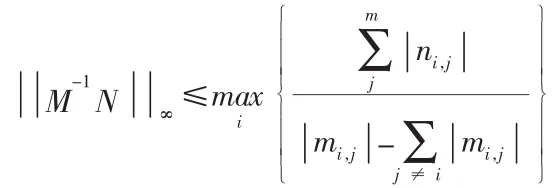
定理1由格式(4)和格式(5)构成的差分格式是绝对稳定的。

证明：对格式(4)和格式(5)的矩阵形式(6)和(7)进行稳定性分析，先分析格式(6)，对于系数矩阵A，由于：

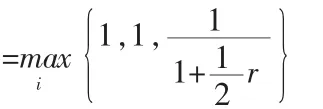
因而，由（4）和（5）构成的差分格式是绝对稳定，定理证毕。

［1］袁光伟,岳晶岩,盛志强,等.非线性抛物型方程计算方法[J].中国科学∶数学,2013(3)∶235-248.

［2］詹涌强,谭志明.求解抛物型方程的一个高精度隐格式[J].西南大学学报∶自然科学版,2013,11∶12.

［3］詹涌强,张传林.解抛物型方程的一个新的高精度隐格式[J].华中师范大学学报∶自然科学版,2014,48(2)∶168∶171.

［4］王自强,曹俊英,宋士仓.半线性抛物型方程改进全离散双尺度有限元分析[J].河南师范大学学报∶自然科学版,2010,38(1)∶41-43.

［5］曹俊英,王自强,复合材料板热传导问题的二阶双尺度算法[J].贵州科学2014,32(3)∶17-20.

［6］Hu Jiagan.The estimates ofand the optimally scaled matrix[J].Journal of Computational Mathematics,1984,2∶122-129.